分式方程的应用
图片预览





文档简介
课件15张PPT。16.3分式方程的应用2——用列表法解工程、行程应用题2009.3.19 解分式方程 解 : 方程两边同乘以(x -1)(x +2),得化简,得 x+2 = 3检验:当x = 1 时,(x+2)(x-1)=0,x =1不是原方程的根.∴ 原分式方程无解 . x(x+2)-(x-1)(x+2)=3解得 x=1 列分式方程解应用题的一般步骤1.审: 1、点明步骤两次检验是:
(1)是否是所列方程的解;
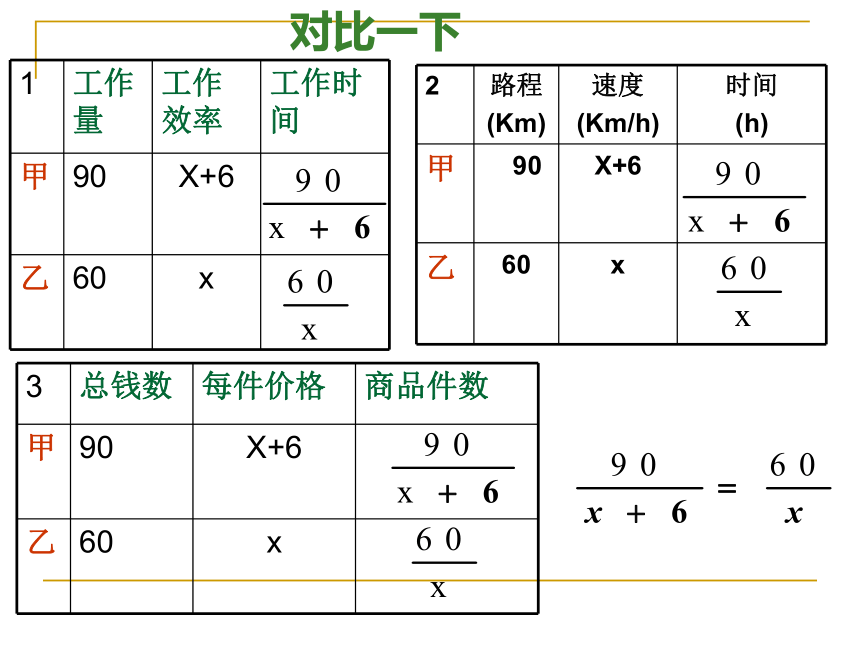
(2)是否满足实际意义.分析题意,找出数量关系和相等关系.2.设:选择恰当的未知数,注意单位和语言完整.3.列:根据数量和相等关系,正确列出代数式和方程.4.解:一化、二解、三检验5.验:6.答:有两次检验.注意单位和语言完整.且答案要生活化. 1、甲、乙两人做某种机器零件,已知甲每小时比乙多做6个,甲做90个零件所用的时间和乙做60个零件所用时间相等,求甲、乙每小时各做多少个零件? 2、 甲、乙两人练习骑自行车,已知甲每小时比乙多走6千米,甲骑90千米所用的时间和乙起骑60千米所用时间相等,求甲、乙每小时各骑多少千米?有什么区别和联系?练一练3、甲、乙两种商品,已知甲的价格每件比乙多6元,90元钱买的甲商品与花60元买的乙商品件数相同,求甲、乙每件商品的价格各多少元?对比一下联系数量关系和所列方程相同即:两个量的积等于第三个量区别一是工作问题,二是行程问题,三是价格问题例题1 两个小组同时开始攀登一座 米高的山,第一组的攀登速度是第二组的 倍,他们比第二组早
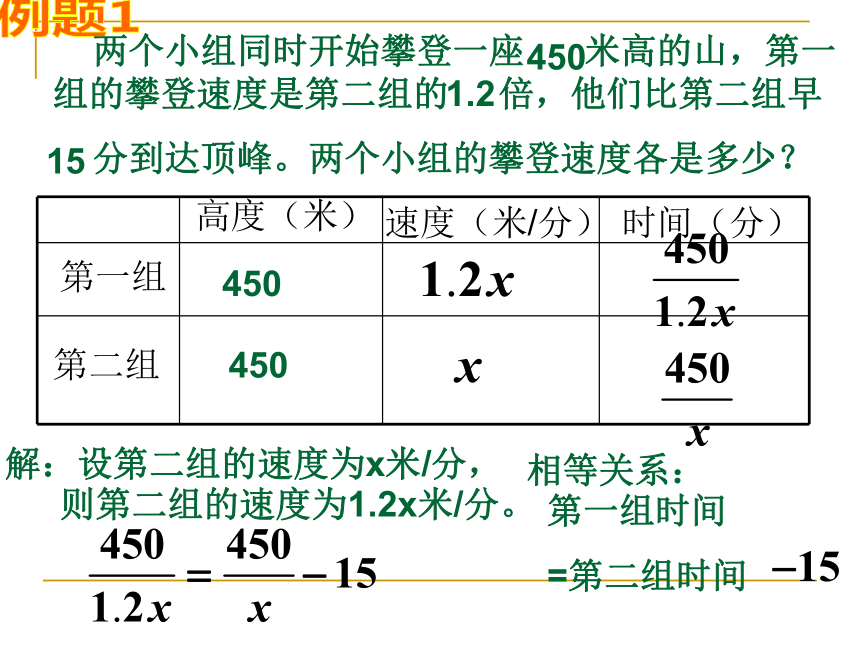
分到达顶峰。两个小组的攀登速度各是多少?4501.215高度(米)速度(米/分)时间(分)第一组第二组450450解:设第二组的速度为x米/分,则第二组的速度为1.2x米/分。相等关系:第一组时间
=第二组时间例题1 两个小组同时开始攀登一座 米高的山,第一组的攀登速度是第二组的 倍,他们比第二组早
分到达顶峰。两个小组的攀登速度各是多少?4501.215高度(米)速度(米/分)时间(分)第一组第二组hh解:设第二组的速度为x米/分,相等关系:第一组时间=
第二组时间检验:
是原方程的根 答:第一组速度为 米/分,
第二组速度为 米/分。 练习1相等关系:小管注水时间+大管注水时间=总时间体积(立方米)速度(立方米/分)时间(分)小水管大水管从2004年5月起某列车平均提速v千米/小时,用相同的时间,列车提速前行驶s千米,提速后比提速前多行驶50千米,提速前列车的平均速度为多少?思考:这是____问题行程等量关系:时间相等路程km速度km/h时间h提速前提速后练习2等量关系:时间相等解:设提速前列车的平均速度为x千米/时由题意,得注意:
s、v的实际意义练习32、解方程求x列分式方程解应用题的方法和步骤如下:1、审题分析题意 2、设未知数
3、根据题意找相等关系,列出方程;
4、解方程,并验根(对解分式方程尤为重要)
5、写答案小结从更高的角度去理解工程、行程及价格问题时我们发现:数量之间具有相同的关系用数学语言讲就是它们属于同一个数学模型中考连接(2006年,贵阳市)甲乙两人加工同一种玩具,甲加工90个玩具所用的时间与乙加工120个玩具所用的时间相等,已知甲乙两人每天共加工35个玩具,求甲乙两人每天各加工多少个玩具?解:设甲每天加工x个玩具,那么乙每天加工(35-x)个玩具,由题意得: 解得: 检验:当x=15时,x(35-x)≠0,所以x=15是原方程的根 .答:甲每天加工15个玩具,乙每天加工20个玩具。 作业33页6,8
(1)是否是所列方程的解;
(2)是否满足实际意义.分析题意,找出数量关系和相等关系.2.设:选择恰当的未知数,注意单位和语言完整.3.列:根据数量和相等关系,正确列出代数式和方程.4.解:一化、二解、三检验5.验:6.答:有两次检验.注意单位和语言完整.且答案要生活化. 1、甲、乙两人做某种机器零件,已知甲每小时比乙多做6个,甲做90个零件所用的时间和乙做60个零件所用时间相等,求甲、乙每小时各做多少个零件? 2、 甲、乙两人练习骑自行车,已知甲每小时比乙多走6千米,甲骑90千米所用的时间和乙起骑60千米所用时间相等,求甲、乙每小时各骑多少千米?有什么区别和联系?练一练3、甲、乙两种商品,已知甲的价格每件比乙多6元,90元钱买的甲商品与花60元买的乙商品件数相同,求甲、乙每件商品的价格各多少元?对比一下联系数量关系和所列方程相同即:两个量的积等于第三个量区别一是工作问题,二是行程问题,三是价格问题例题1 两个小组同时开始攀登一座 米高的山,第一组的攀登速度是第二组的 倍,他们比第二组早
分到达顶峰。两个小组的攀登速度各是多少?4501.215高度(米)速度(米/分)时间(分)第一组第二组450450解:设第二组的速度为x米/分,则第二组的速度为1.2x米/分。相等关系:第一组时间
=第二组时间例题1 两个小组同时开始攀登一座 米高的山,第一组的攀登速度是第二组的 倍,他们比第二组早
分到达顶峰。两个小组的攀登速度各是多少?4501.215高度(米)速度(米/分)时间(分)第一组第二组hh解:设第二组的速度为x米/分,相等关系:第一组时间=
第二组时间检验:
是原方程的根 答:第一组速度为 米/分,
第二组速度为 米/分。 练习1相等关系:小管注水时间+大管注水时间=总时间体积(立方米)速度(立方米/分)时间(分)小水管大水管从2004年5月起某列车平均提速v千米/小时,用相同的时间,列车提速前行驶s千米,提速后比提速前多行驶50千米,提速前列车的平均速度为多少?思考:这是____问题行程等量关系:时间相等路程km速度km/h时间h提速前提速后练习2等量关系:时间相等解:设提速前列车的平均速度为x千米/时由题意,得注意:
s、v的实际意义练习32、解方程求x列分式方程解应用题的方法和步骤如下:1、审题分析题意 2、设未知数
3、根据题意找相等关系,列出方程;
4、解方程,并验根(对解分式方程尤为重要)
5、写答案小结从更高的角度去理解工程、行程及价格问题时我们发现:数量之间具有相同的关系用数学语言讲就是它们属于同一个数学模型中考连接(2006年,贵阳市)甲乙两人加工同一种玩具,甲加工90个玩具所用的时间与乙加工120个玩具所用的时间相等,已知甲乙两人每天共加工35个玩具,求甲乙两人每天各加工多少个玩具?解:设甲每天加工x个玩具,那么乙每天加工(35-x)个玩具,由题意得: 解得: 检验:当x=15时,x(35-x)≠0,所以x=15是原方程的根 .答:甲每天加工15个玩具,乙每天加工20个玩具。 作业33页6,8
