专题复习:如何求二次函数的解析式(四川省宜宾市)
文档属性
| 名称 | 专题复习:如何求二次函数的解析式(四川省宜宾市) |  | |
| 格式 | rar | ||
| 文件大小 | 381.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-03-20 19:49:00 | ||
图片预览






文档简介
课件15张PPT。2009-3-18专题复习:
如何求二次函数的解析式宜宾市二中曾 丹?二次函数的定义是什么? 如何求二次函数的
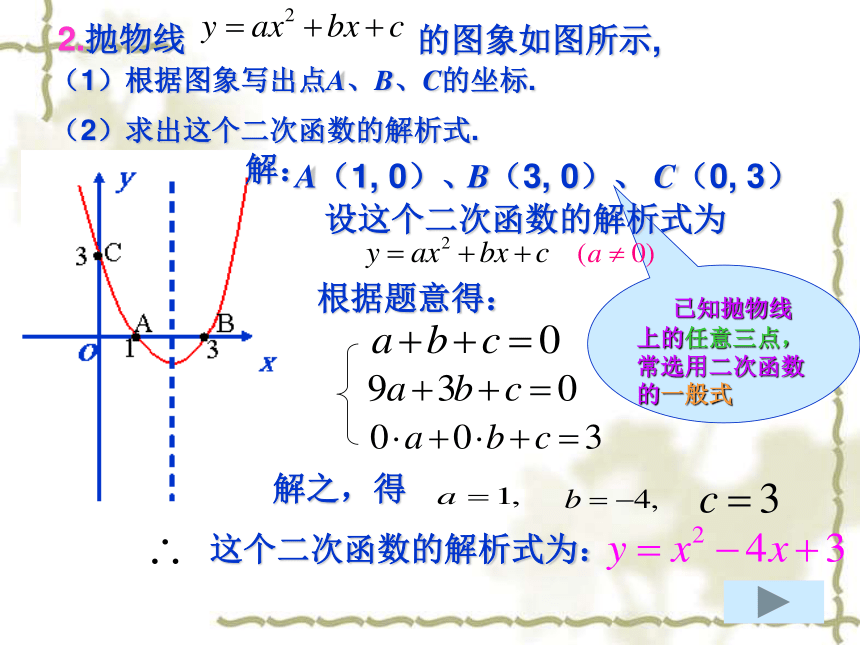
解析式呢?1.已知函数是二次函数,求这个二次函数的解析式.解:由题意得:解之,得:m=-1这个二次函数的解析式为: 利用二次函数的定义求解析式2.抛物线的图象如图所示,(2)求出这个二次函数的解析式.(1)根据图象写出点A、B、C的坐标.A(1, 0)、B(3, 0)、C(0, 3) 已知抛物线上的任意三点,常选用二次函数的一般式
解:设这个二次函数的解析式为根据题意得: 解之,得这个二次函数的解析式为:2.抛物线的图象如图所示,(2)求出这个二次函数的解析式. 已知抛物线与x轴的交点,可选用两根式
(1)根据图象写出点A、B、C的坐标.A(1, 0)、B(3, 0)、C(0, 3)解:设这个二次函数的解析式为:解之,得这个二次函数的解析式为: 3. 一个二次函数的图象过点(0, 1),它的顶点坐标
是(8, 9),求这个二次函数的解析式.分析:已知顶点坐标,设顶点式解:设这个二次函数的解析式为:抛物线过点(0, 1)解之,得这个二次函数的解析式为: 已知二次函数的顶点坐标或对称轴或最值设顶点式.4.把函数的图象沿x轴对折得到的图象的解析式是分析:关于x轴对称法2:顶点坐标:(1, 2)关于x轴对称(1, -2)抛物线开口方向改变,张口大小没变5.将抛物线的图象向上平移3 个单位,再向右平移4个单位得到的抛物线是分析:将配成顶点式:向上平移3个单位向右平移4个单位上+下-左+右-法2:顶点坐标(1, 1)向上平移3个单位(1, 4)向右平移4个单位(5, 4)6.抛物线绕其顶点旋转将得到怎样的抛物线?试求出其解析式.分析:抛物线开口方向改变,张口大小没变抛物线顶点没变顶点坐标:(3,2)(3,2)旋转前:旋转后:即:7.(宜宾 2008年)已知:如图,抛物线y=-x2+bx+c与x轴、y轴分别
相交于点A(-1,0)、B(0,3)两点,其顶点为D.
(1)求该抛物线的解析式;(2)若该抛物线与x轴的另一个交点为E. 求四边形ABDE的面积;
(3)△AOB与△BDE是否相似?如果相似,请予以证明;如果不相似,请说明理由.
分析:课堂小结在求二次函数解析式时应注意哪几个方面?要视题目的已知条件,选用适当的解析式;选用的方法应使未知数的个数越少越好,未知数的次数也是越低越方便。注意二次函数与一元二次方程的联系,通过数形结合,可把二次函数的问题转化为一元二次方程的知识来解决。作业:教材1,2题谢谢大家!2.抛物线的图象如图所示,(2)求出这个二次函数的解析式.(1)根据图象写出点A、B、C的坐标.A(1, 0)、B(3, 0)、C(0, 3) 已知抛物线上的任意三点,常选用二次函数的一般式
解:设这个二次函数的解析式为根据题意得: 解之,得这个二次函数的解析式为:
解析式呢?1.已知函数是二次函数,求这个二次函数的解析式.解:由题意得:解之,得:m=-1这个二次函数的解析式为: 利用二次函数的定义求解析式2.抛物线的图象如图所示,(2)求出这个二次函数的解析式.(1)根据图象写出点A、B、C的坐标.A(1, 0)、B(3, 0)、C(0, 3) 已知抛物线上的任意三点,常选用二次函数的一般式
解:设这个二次函数的解析式为根据题意得: 解之,得这个二次函数的解析式为:2.抛物线的图象如图所示,(2)求出这个二次函数的解析式. 已知抛物线与x轴的交点,可选用两根式
(1)根据图象写出点A、B、C的坐标.A(1, 0)、B(3, 0)、C(0, 3)解:设这个二次函数的解析式为:解之,得这个二次函数的解析式为: 3. 一个二次函数的图象过点(0, 1),它的顶点坐标
是(8, 9),求这个二次函数的解析式.分析:已知顶点坐标,设顶点式解:设这个二次函数的解析式为:抛物线过点(0, 1)解之,得这个二次函数的解析式为: 已知二次函数的顶点坐标或对称轴或最值设顶点式.4.把函数的图象沿x轴对折得到的图象的解析式是分析:关于x轴对称法2:顶点坐标:(1, 2)关于x轴对称(1, -2)抛物线开口方向改变,张口大小没变5.将抛物线的图象向上平移3 个单位,再向右平移4个单位得到的抛物线是分析:将配成顶点式:向上平移3个单位向右平移4个单位上+下-左+右-法2:顶点坐标(1, 1)向上平移3个单位(1, 4)向右平移4个单位(5, 4)6.抛物线绕其顶点旋转将得到怎样的抛物线?试求出其解析式.分析:抛物线开口方向改变,张口大小没变抛物线顶点没变顶点坐标:(3,2)(3,2)旋转前:旋转后:即:7.(宜宾 2008年)已知:如图,抛物线y=-x2+bx+c与x轴、y轴分别
相交于点A(-1,0)、B(0,3)两点,其顶点为D.
(1)求该抛物线的解析式;(2)若该抛物线与x轴的另一个交点为E. 求四边形ABDE的面积;
(3)△AOB与△BDE是否相似?如果相似,请予以证明;如果不相似,请说明理由.
分析:课堂小结在求二次函数解析式时应注意哪几个方面?要视题目的已知条件,选用适当的解析式;选用的方法应使未知数的个数越少越好,未知数的次数也是越低越方便。注意二次函数与一元二次方程的联系,通过数形结合,可把二次函数的问题转化为一元二次方程的知识来解决。作业:教材1,2题谢谢大家!2.抛物线的图象如图所示,(2)求出这个二次函数的解析式.(1)根据图象写出点A、B、C的坐标.A(1, 0)、B(3, 0)、C(0, 3) 已知抛物线上的任意三点,常选用二次函数的一般式
解:设这个二次函数的解析式为根据题意得: 解之,得这个二次函数的解析式为:
