5.2平行线及其判定 同步练习题(含解析)人教版七年级数学下册
文档属性
| 名称 | 5.2平行线及其判定 同步练习题(含解析)人教版七年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 372.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-16 13:26:34 | ||
图片预览


文档简介
人教版七年级数学下册《5.2平行线及其判定》同步练习题(附答案)
一、单选题
1.下列说法错误的是( )
A.在同一平面内,a,b,c是直线,且,,则
B.在同一平面内,a,b,c是直线,且,,则
C.在同一平面内,a,b,c是直线,且,,则
D.在同一平面内,a,b,c是直线,且,,则
2.如图,可以判定的条件是( )
A. B. C. D.
3.下列各图中,已知,则可以得到的是( )
A. B.
C. D.
4.如图,课本上用直尺和三角尺画平行线的方法,其依据是( )
A.两直线平行,同位角相等 B.同位角相等,两直线平行
C.两直线平行,内错角相等 D.内错角相等,两直线平行
5.如图,点在直线上,已知,,若要使得,则( )
A. B. C. D.
6.如图,下列说理中,正确的是( )
A.因为,所以 B.因为,所以
C.因为,所以 D.因为,所以
7.如图,将一纸条沿折痕折叠,时对应线段与相交于点则下列条件中,不足以证明的是( )
A. B.
C. D.
8.如图,有下列条件:①;②平分,;③;④,.其中,能够得到的条件个数是( ).
A.1个 B.2个 C.3个 D.4个
二、填空题
9.如图,直线,被直线c所截,若∠4+∠5=180°,则可得∥,其依据是: .
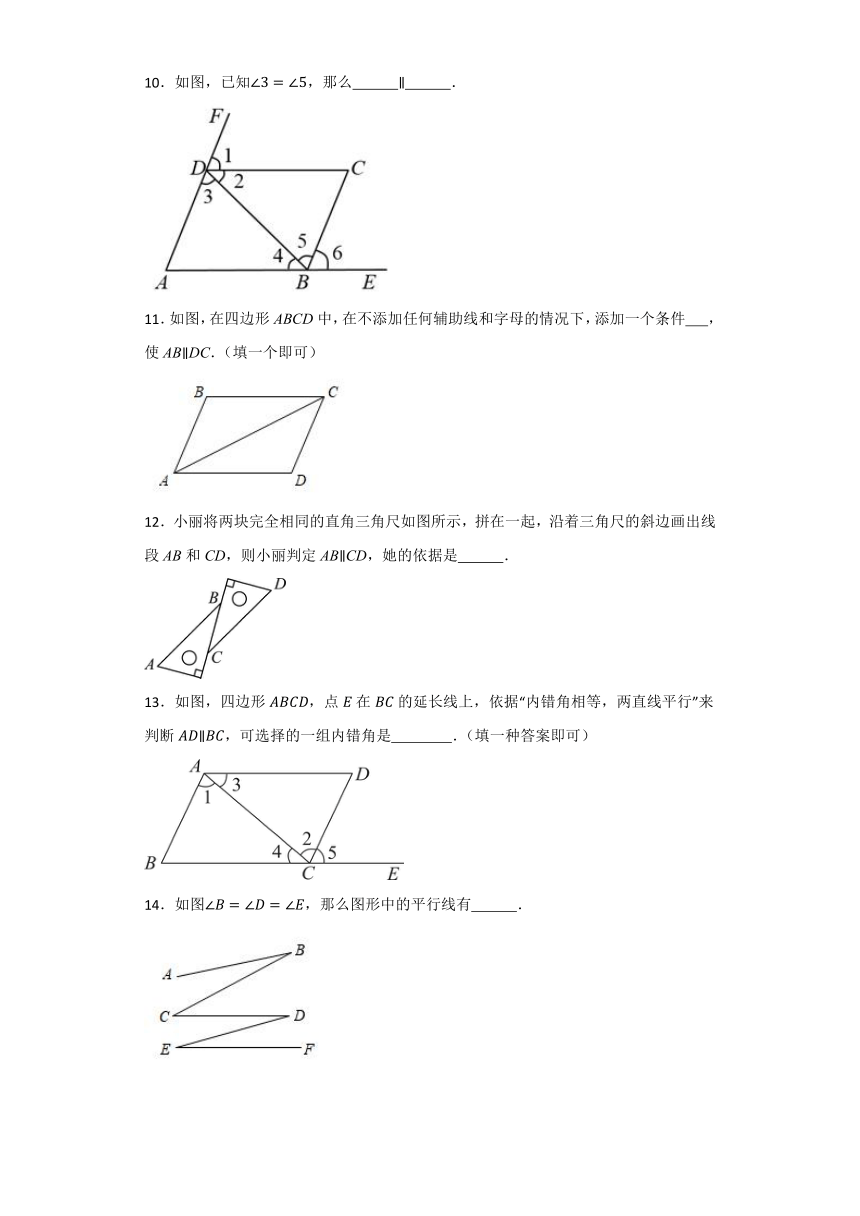
10.如图,已知,那么 .
11.如图,在四边形ABCD中,在不添加任何辅助线和字母的情况下,添加一个条件 ,使ABDC.(填一个即可)
12.小丽将两块完全相同的直角三角尺如图所示,拼在一起,沿着三角尺的斜边画出线段AB和CD,则小丽判定ABCD,她的依据是 .
13.如图,四边形,点在的延长线上,依据“内错角相等,两直线平行”来判断,可选择的一组内错角是 .(填一种答案即可)
14.如图,那么图形中的平行线有 .
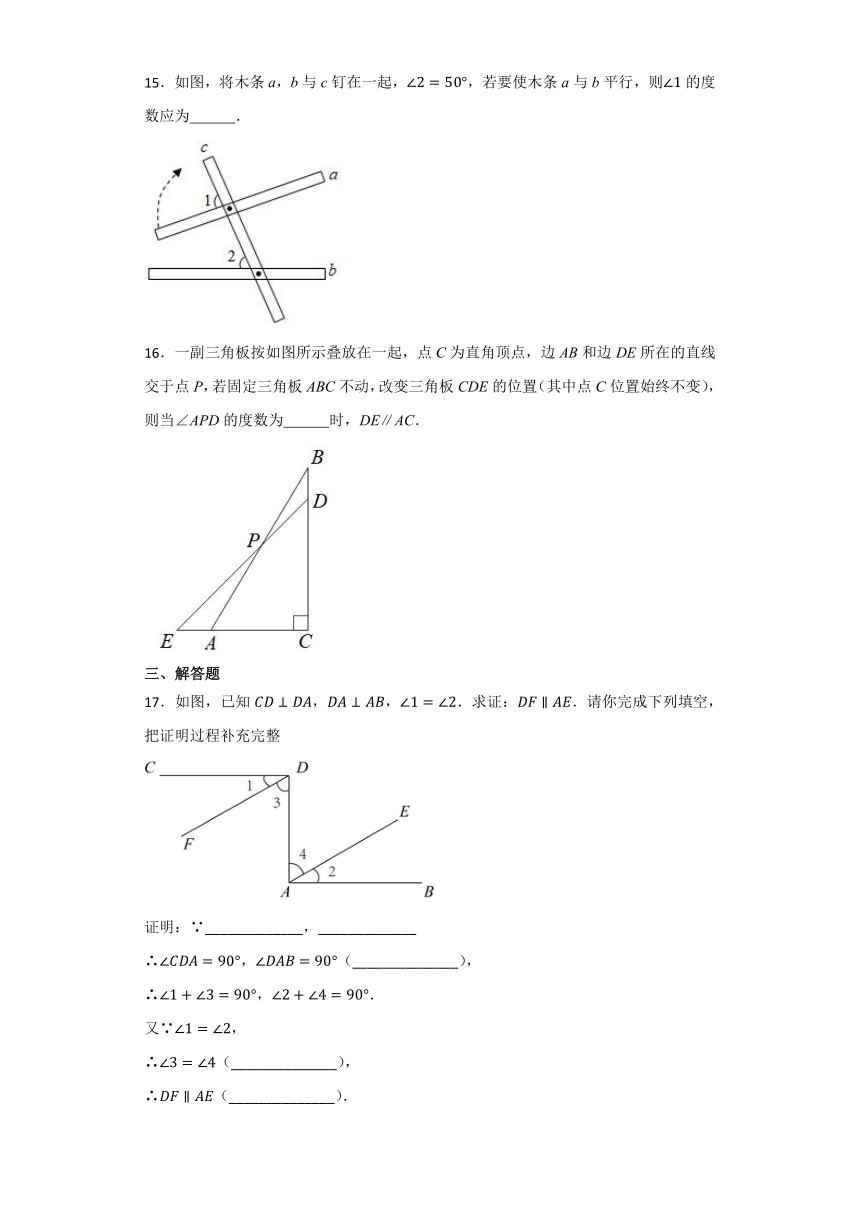
15.如图,将木条a,b与c钉在一起,,若要使木条a与b平行,则的度数应为 .
16.一副三角板按如图所示叠放在一起,点C为直角顶点,边AB和边DE所在的直线交于点P,若固定三角板ABC不动,改变三角板CDE的位置(其中点C位置始终不变),则当∠APD的度数为 时,DE∥AC.
三、解答题
17.如图,已知,,.求证:.请你完成下列填空,把证明过程补充完整
证明:∵_____________,_____________
∴,(______________),
∴,.
又∵,
∴(______________),
∴(______________).
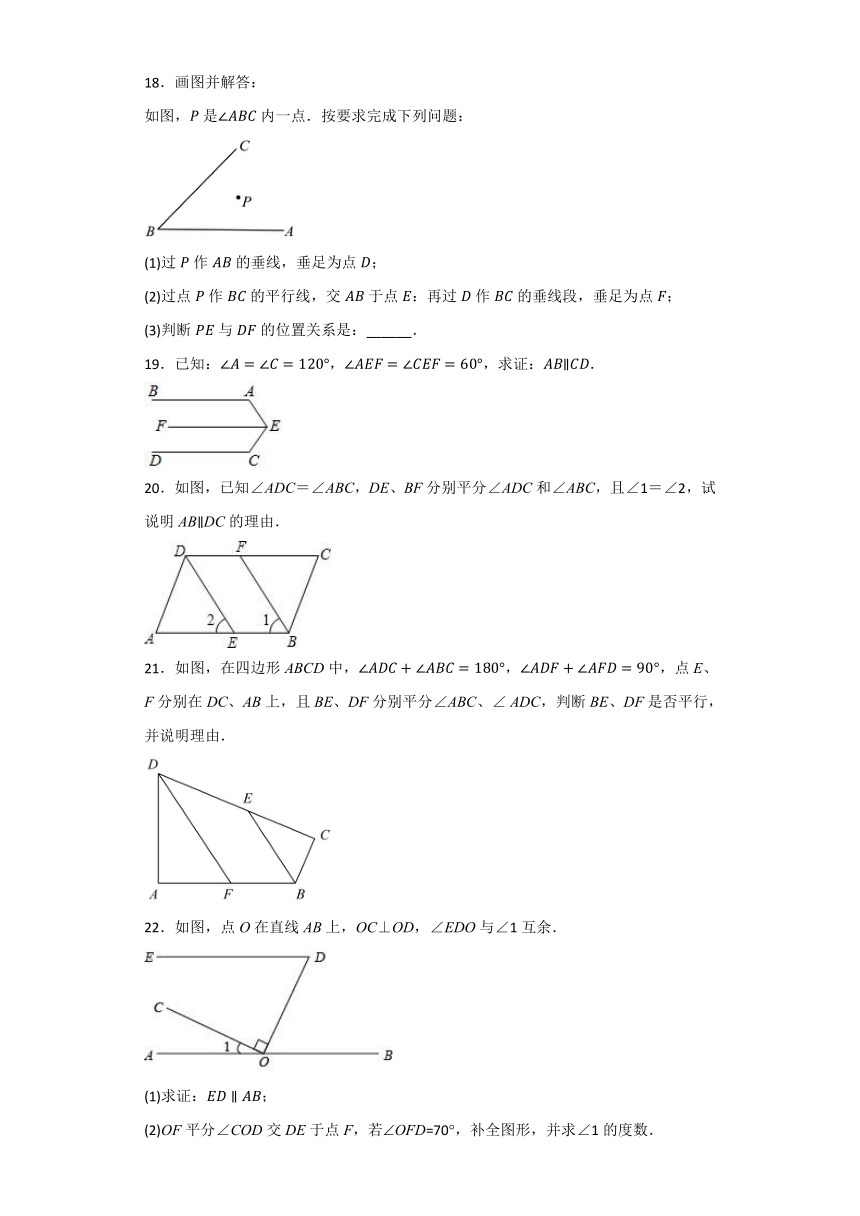
18.画图并解答:
如图,是内一点.按要求完成下列问题:
(1)过作的垂线,垂足为点;
(2)过点作的平行线,交于点:再过作的垂线段,垂足为点;
(3)判断与的位置关系是:______.
19.已知:,,求证:.
20.如图,已知∠ADC=∠ABC,DE、BF分别平分∠ADC和∠ABC,且∠1=∠2,试说明ABDC的理由.
21.如图,在四边形ABCD中,,,点E、F分别在DC、AB上,且BE、DF分别平分∠ABC、∠ ADC,判断BE、DF是否平行,并说明理由.
22.如图,点O在直线AB上,OC⊥OD,∠EDO与∠1互余.
(1)求证:;
(2)OF平分∠COD交DE于点F,若OFD=70,补全图形,并求∠1的度数.
23.如图,已知,.
(1)试判断BF与DE的位置关系,并说明理由;
(2)若,,求∠AFG的度数.
参考答案
1.解:A、在同一平面内,a,b,c是直线,且,,则,故该说法正确,不符合题意;
B、在同一平面内,a,b,c是直线,且,,则,故该说法正确,不符合题意;
C、在同一平面内,a,b,c是直线,且,,则,故原说法错误,符合题意;
D、在同一平面内,a,b,c是直线,且,,则,故该说法正确,不符合题意.
故选:C
2.解:∵,
∴(内错角相等,两直线平行),
故A选项不符合题意;
∵,
∴(内错角相等,两直线平行),
故B选项符合题意;
不符合平行线的判断条件,所以不能判断直线,
故C选项不符合题意;
不符合平行线的判断条件,所以不能判断直线,
故D选项不符合题意;
故选:B.
3.解:A、,,,
,
,符合题意,选项正确;
B、不能得到,不符合题意,选项错误;
C、不能得到,不符合题意,选项错误;
D、不能得到,不符合题意,选项错误,
故选A.
4.解:如图所示,与为同位角.
由作法可得
,
∴(同位角相等,两直线平行).
故选:B.
5.解:当时,
∵,
∴,
∴,
故选C.
6.解:A、由,无法判定,故不合题意;
B、由,无法判定,故不合题意;
C、由,可判定,故符合题意;
D、由,无法判定,故不合题意;
故选C.
7.解:A. ,
;
B.由翻折可知:,
,
,
,故B选项不符合题意;
C.由翻折可知:,
,
,
,
,故C选项不符合题意;
,
,
,
不平行,故D选项符合题意;
故选:D.
8.解:由,可由内错角相等,两直线平行得到,不能得到,故①不符合题意;
由平分,可推出,可由内错角相等,两直线平行得到,故②符合题意;
由,可推出,可由内错角相等,两直线平行得到,故③符合题意;
由可得,再由可推出,可由同旁内角互补,两直线平行得到,故④符合题意;
故选C.
9.解:根据题意,直线,被直线c所截,若∠4+∠5=180°,则可得∥,其依据是:同旁内角互补,两直线平行
故答案为:同旁内角互补,两直线平行.
10.解:∵(已知)
∴(内错角相等,两直线平行)
11.解:给定条件BAC=DCA,
∴ABDC(内错角相等两条直线平行).
故答案为:BAC=DCA.
12.解:由题意:∠BCD=∠ABC=30°,
∴ABCD(内错角相等,两直线平行),
故答案为:内错角相等,两直线平行.
13.解:
或
故答案为:或(任写一组即可)
14.解:∵∠D=∠E,
∴CD∥EF.
故答案为:CD∥EF.
15.解:∵∠1=∠2时,a∥b,
∴若要使木条a与b平行,∠1=∠2=50°,
故答案为:50°.
16.解:三角板CDE转动到DE∥AC的情况,如图
,
DE∥AC,
,
故答案为:.
17.证明:∵,,
∴,(垂直的定义)
∴,,
又∵
∴(等角的余角相等),
∴(内错角相等,两直线平行).
18.(1)解:如图,直线即为所求;
(2)如图,直线,线段即为所求;
(3),,
,
故答案为:垂直.
19.证明:,,
,,
,,
.
20.解:ABDC.
理由如下:
∵DE、BF分别平分∠ADC和∠ABC,
∴,,
∵∠ADC=∠ABC,
∴∠CDE=∠1,
∵∠1=∠2,
∴∠CDE=∠2,
∴ABDC.
21.解:,理由如下:
分别平分,
,
,
,
又,
,
.
22.(1)证明:
∵与互余
∴
又∵
∴
∵
又∵
∴.
(2)∵平分交于点
∴
∵
∴在中,
∴
∴
又∵与互余
∴
∴
∴.
23.(1)解:BF∥DE,理由如下:
∵,.
∴.
∴BF∥DE;
(2)解:∵,,
∴∠1=40°,
∵,
∴∠AFB=90°,
∴∠AFG=∠AFB-∠1=50°.
一、单选题
1.下列说法错误的是( )
A.在同一平面内,a,b,c是直线,且,,则
B.在同一平面内,a,b,c是直线,且,,则
C.在同一平面内,a,b,c是直线,且,,则
D.在同一平面内,a,b,c是直线,且,,则
2.如图,可以判定的条件是( )
A. B. C. D.
3.下列各图中,已知,则可以得到的是( )
A. B.
C. D.
4.如图,课本上用直尺和三角尺画平行线的方法,其依据是( )
A.两直线平行,同位角相等 B.同位角相等,两直线平行
C.两直线平行,内错角相等 D.内错角相等,两直线平行
5.如图,点在直线上,已知,,若要使得,则( )
A. B. C. D.
6.如图,下列说理中,正确的是( )
A.因为,所以 B.因为,所以
C.因为,所以 D.因为,所以
7.如图,将一纸条沿折痕折叠,时对应线段与相交于点则下列条件中,不足以证明的是( )
A. B.
C. D.
8.如图,有下列条件:①;②平分,;③;④,.其中,能够得到的条件个数是( ).
A.1个 B.2个 C.3个 D.4个
二、填空题
9.如图,直线,被直线c所截,若∠4+∠5=180°,则可得∥,其依据是: .
10.如图,已知,那么 .
11.如图,在四边形ABCD中,在不添加任何辅助线和字母的情况下,添加一个条件 ,使ABDC.(填一个即可)
12.小丽将两块完全相同的直角三角尺如图所示,拼在一起,沿着三角尺的斜边画出线段AB和CD,则小丽判定ABCD,她的依据是 .
13.如图,四边形,点在的延长线上,依据“内错角相等,两直线平行”来判断,可选择的一组内错角是 .(填一种答案即可)
14.如图,那么图形中的平行线有 .
15.如图,将木条a,b与c钉在一起,,若要使木条a与b平行,则的度数应为 .
16.一副三角板按如图所示叠放在一起,点C为直角顶点,边AB和边DE所在的直线交于点P,若固定三角板ABC不动,改变三角板CDE的位置(其中点C位置始终不变),则当∠APD的度数为 时,DE∥AC.
三、解答题
17.如图,已知,,.求证:.请你完成下列填空,把证明过程补充完整
证明:∵_____________,_____________
∴,(______________),
∴,.
又∵,
∴(______________),
∴(______________).
18.画图并解答:
如图,是内一点.按要求完成下列问题:
(1)过作的垂线,垂足为点;
(2)过点作的平行线,交于点:再过作的垂线段,垂足为点;
(3)判断与的位置关系是:______.
19.已知:,,求证:.
20.如图,已知∠ADC=∠ABC,DE、BF分别平分∠ADC和∠ABC,且∠1=∠2,试说明ABDC的理由.
21.如图,在四边形ABCD中,,,点E、F分别在DC、AB上,且BE、DF分别平分∠ABC、∠ ADC,判断BE、DF是否平行,并说明理由.
22.如图,点O在直线AB上,OC⊥OD,∠EDO与∠1互余.
(1)求证:;
(2)OF平分∠COD交DE于点F,若OFD=70,补全图形,并求∠1的度数.
23.如图,已知,.
(1)试判断BF与DE的位置关系,并说明理由;
(2)若,,求∠AFG的度数.
参考答案
1.解:A、在同一平面内,a,b,c是直线,且,,则,故该说法正确,不符合题意;
B、在同一平面内,a,b,c是直线,且,,则,故该说法正确,不符合题意;
C、在同一平面内,a,b,c是直线,且,,则,故原说法错误,符合题意;
D、在同一平面内,a,b,c是直线,且,,则,故该说法正确,不符合题意.
故选:C
2.解:∵,
∴(内错角相等,两直线平行),
故A选项不符合题意;
∵,
∴(内错角相等,两直线平行),
故B选项符合题意;
不符合平行线的判断条件,所以不能判断直线,
故C选项不符合题意;
不符合平行线的判断条件,所以不能判断直线,
故D选项不符合题意;
故选:B.
3.解:A、,,,
,
,符合题意,选项正确;
B、不能得到,不符合题意,选项错误;
C、不能得到,不符合题意,选项错误;
D、不能得到,不符合题意,选项错误,
故选A.
4.解:如图所示,与为同位角.
由作法可得
,
∴(同位角相等,两直线平行).
故选:B.
5.解:当时,
∵,
∴,
∴,
故选C.
6.解:A、由,无法判定,故不合题意;
B、由,无法判定,故不合题意;
C、由,可判定,故符合题意;
D、由,无法判定,故不合题意;
故选C.
7.解:A. ,
;
B.由翻折可知:,
,
,
,故B选项不符合题意;
C.由翻折可知:,
,
,
,
,故C选项不符合题意;
,
,
,
不平行,故D选项符合题意;
故选:D.
8.解:由,可由内错角相等,两直线平行得到,不能得到,故①不符合题意;
由平分,可推出,可由内错角相等,两直线平行得到,故②符合题意;
由,可推出,可由内错角相等,两直线平行得到,故③符合题意;
由可得,再由可推出,可由同旁内角互补,两直线平行得到,故④符合题意;
故选C.
9.解:根据题意,直线,被直线c所截,若∠4+∠5=180°,则可得∥,其依据是:同旁内角互补,两直线平行
故答案为:同旁内角互补,两直线平行.
10.解:∵(已知)
∴(内错角相等,两直线平行)
11.解:给定条件BAC=DCA,
∴ABDC(内错角相等两条直线平行).
故答案为:BAC=DCA.
12.解:由题意:∠BCD=∠ABC=30°,
∴ABCD(内错角相等,两直线平行),
故答案为:内错角相等,两直线平行.
13.解:
或
故答案为:或(任写一组即可)
14.解:∵∠D=∠E,
∴CD∥EF.
故答案为:CD∥EF.
15.解:∵∠1=∠2时,a∥b,
∴若要使木条a与b平行,∠1=∠2=50°,
故答案为:50°.
16.解:三角板CDE转动到DE∥AC的情况,如图
,
DE∥AC,
,
故答案为:.
17.证明:∵,,
∴,(垂直的定义)
∴,,
又∵
∴(等角的余角相等),
∴(内错角相等,两直线平行).
18.(1)解:如图,直线即为所求;
(2)如图,直线,线段即为所求;
(3),,
,
故答案为:垂直.
19.证明:,,
,,
,,
.
20.解:ABDC.
理由如下:
∵DE、BF分别平分∠ADC和∠ABC,
∴,,
∵∠ADC=∠ABC,
∴∠CDE=∠1,
∵∠1=∠2,
∴∠CDE=∠2,
∴ABDC.
21.解:,理由如下:
分别平分,
,
,
,
又,
,
.
22.(1)证明:
∵与互余
∴
又∵
∴
∵
又∵
∴.
(2)∵平分交于点
∴
∵
∴在中,
∴
∴
又∵与互余
∴
∴
∴.
23.(1)解:BF∥DE,理由如下:
∵,.
∴.
∴BF∥DE;
(2)解:∵,,
∴∠1=40°,
∵,
∴∠AFB=90°,
∴∠AFG=∠AFB-∠1=50°.
