5.3平行线的性质 同步练习题(含解析)人教版数学七年级下册
文档属性
| 名称 | 5.3平行线的性质 同步练习题(含解析)人教版数学七年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 364.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-16 13:25:24 | ||
图片预览


文档简介
人教版七年级数学下册《5.3平行线的性质》同步练习题(附答案)
一.选择题(共8小题)
1.观察下列命题:
(1)如果a<0,b>0,那么a+b<0;
(2)直角都相等;
(3)同角的补角相等;
(4)如果两条直线被第三条直线所截,那么同位角相等.
其中真命题的个数是( )
A.0 B.1 C.2 D.3
2.如图,a∥b,∠1=42°,则∠2的度数为( )
A.48° B.42° C.138° D.52°
3.如图,直线a∥b,直线AB⊥AC,若∠1=50°,则∠2=( )
A.30° B.40° C.45° D.50°
4.如图,将三角尺的直角顶点放在直尺的一边上,若∠1=60°15′,则∠2的大小为( )
A.60°15′ B.39°45′ C.29°85′ D.29°45′
5.如图,将直尺与含45°角的直角三角形叠放在一起,若∠2=35°,则∠1的度数为( )
A.35° B.45° C.55° D.65°
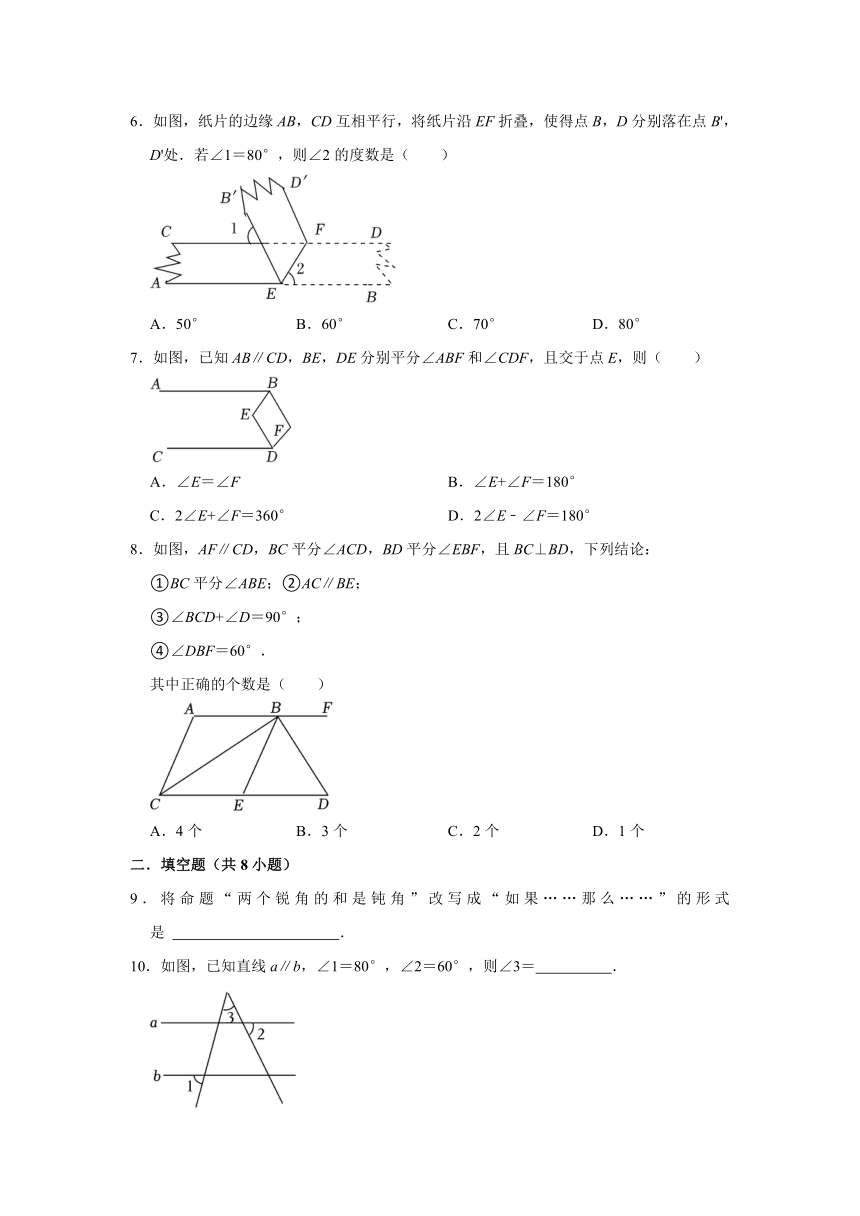
6.如图,纸片的边缘AB,CD互相平行,将纸片沿EF折叠,使得点B,D分别落在点B',D'处.若∠1=80°,则∠2的度数是( )
A.50° B.60° C.70° D.80°
7.如图,已知AB∥CD,BE,DE分别平分∠ABF和∠CDF,且交于点E,则( )
A.∠E=∠F B.∠E+∠F=180°
C.2∠E+∠F=360° D.2∠E﹣∠F=180°
8.如图,AF∥CD,BC平分∠ACD,BD平分∠EBF,且BC⊥BD,下列结论:
①BC平分∠ABE;②AC∥BE;
③∠BCD+∠D=90°;
④∠DBF=60°.
其中正确的个数是( )
A.4个 B.3个 C.2个 D.1个
二.填空题(共8小题)
9.将命题“两个锐角的和是钝角”改写成“如果……那么……”的形式是 .
10.如图,已知直线a∥b,∠1=80°,∠2=60°,则∠3= .
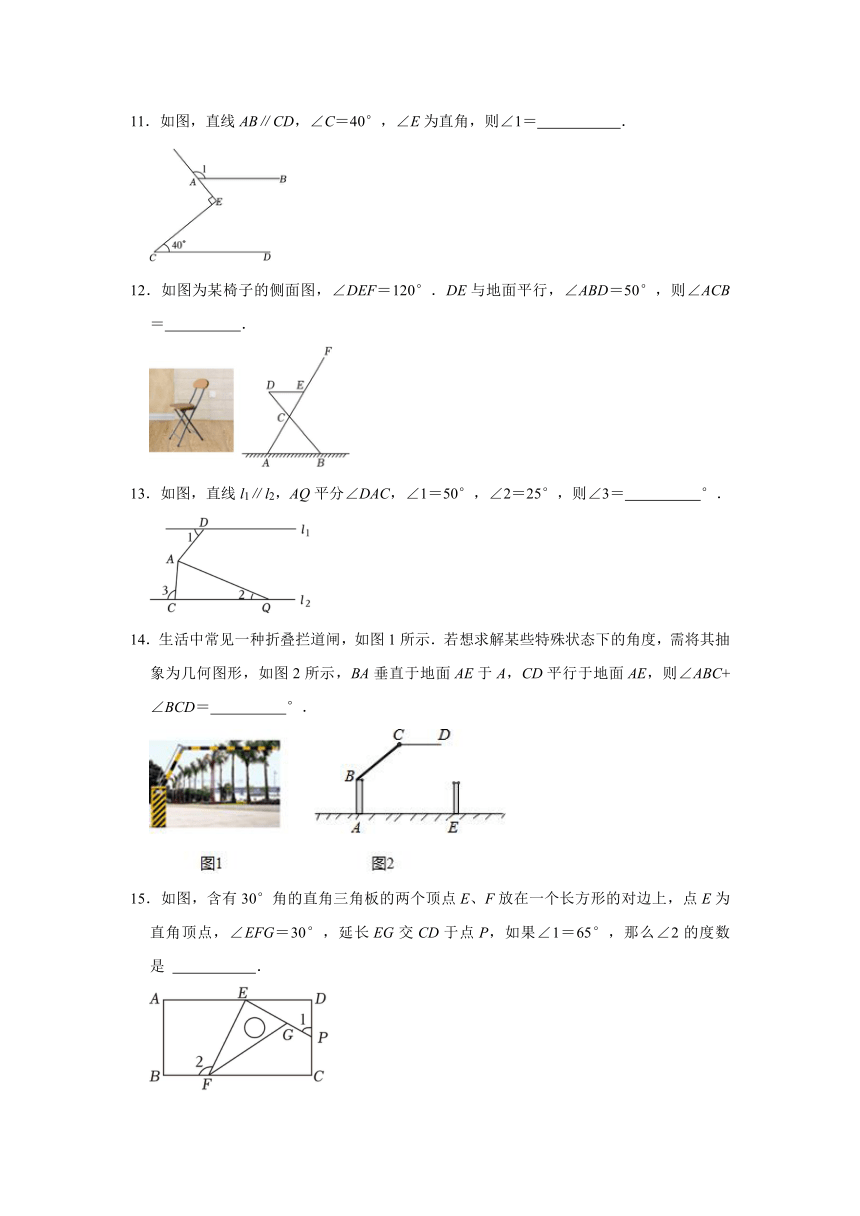
11.如图,直线AB∥CD,∠C=40°,∠E为直角,则∠1= .
12.如图为某椅子的侧面图,∠DEF=120°.DE与地面平行,∠ABD=50°,则∠ACB= .
13.如图,直线l1∥l2,AQ平分∠DAC,∠1=50°,∠2=25°,则∠3= °.
14.生活中常见一种折叠拦道闸,如图1所示.若想求解某些特殊状态下的角度,需将其抽象为几何图形,如图2所示,BA垂直于地面AE于A,CD平行于地面AE,则∠ABC+∠BCD= °.
15.如图,含有30°角的直角三角板的两个顶点E、F放在一个长方形的对边上,点E为直角顶点,∠EFG=30°,延长EG交CD于点P,如果∠1=65°,那么∠2的度数是 .
16.如图,AB∥CD,∠DCE的角平分线CG的反向延长线和∠ABE的角平分线BF交于点F,∠E﹣∠F=60°,则∠E= .
三.解答题(共6小题)
17.如图,A、B、C三点在同一直线上,∠1=∠2,∠3=∠D.求证:BD∥CE.
18.如图,已知EF∥CD,数学课上,老师请同学们根据图形特征添加一个关于角的条件,使得∠BEF=∠CDG,并给出证明过程.
小明添加的条件:∠B=∠ADG.
请你帮小明将下面的证明过程补充完整.
证明:∵EF∥CD( )
∴∠BEF= ( )
∵∠B=∠ADG(添加条件)
∴BC∥ ( )
∴∠CDG= ( )
∴∠BEF=∠CDG ( ).
19.请把以下证明过程补充完整,并在下面的括号内填上推理理由:
已知:如图,∠1=∠2,∠A=∠D.
求证:∠B=∠C
证明:∵∠1=∠2,(已知)
又:∵∠1=∠3,
∴∠2= ,(等量代换)
∴AE∥FD
∴∠A=∠BFD
∵∠A=∠D(已知)
∴∠D= (等量代换)
∴ ∥CD
∴∠B=∠C .
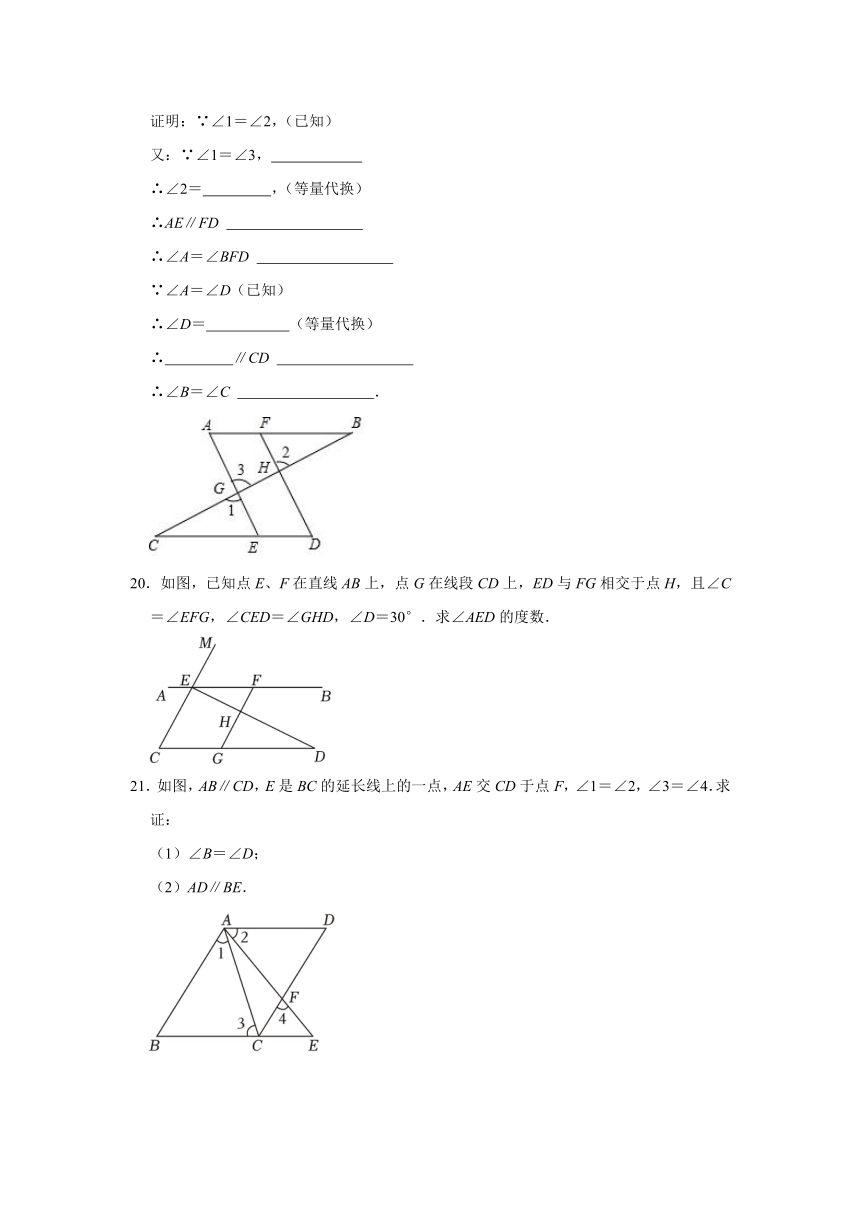
20.如图,已知点E、F在直线AB上,点G在线段CD上,ED与FG相交于点H,且∠C=∠EFG,∠CED=∠GHD,∠D=30°.求∠AED的度数.
21.如图,AB∥CD,E是BC的延长线上的一点,AE交CD于点F,∠1=∠2,∠3=∠4.求证:
(1)∠B=∠D;
(2)AD∥BE.
22.如图,已知AM∥BN,∠A=60°,P是射线AM上一动点(与点A不重合),BC,BD分别平分∠ABP和∠PBN,交射线AM于点C,D.
(1)求∠ABN和∠CBD的度数;
(2)当点P运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若不变,请写出它们之间的关系,并说明理由;若变化,请写出变化规律;
(3)当点P运动到使∠ACB=∠ABD时,求∠ABC的度数.
参考答案
一.选择题(共8小题)
1.解:(1)如果a<0,b>0,那么a+b<0当a=﹣1,b=2时错误,为假命题;
(2)直角都相等,正确,为真命题;
(3)同角的补角相等,正确,为真命题;
(4)如果两条平行直线被第三条直线所截,那么同位角相等,故错误,为假命题,
故选:C.
2.解:∵∠1=∠3=42°,a∥b,
∴∠2=∠3=42°,
故选:B.
3.解:∵直线a∥b,∠1=50°,
∴∠1=∠3=50°,
∵直线AB⊥AC,
∴∠2+∠3=90°.
∴∠2=40°.
故选:B.
4.解:如图,
由直尺两边平行,可得:∠1=∠3=60°15',
∴∠2=90°﹣∠3=90°﹣60°15'=29°45',
故选:D.
5.解:如图,
∵∠ACB=90°,∠2=35°,
∴∠3=90°﹣∠2=90°﹣35°=55°,
∵直尺对边平行,
∴∠1=∠3=55°.
故选:C.
6.解:∵AB∥CD,
∴∠1=∠AEB′=80°,
∴∠BEB′=180°﹣∠AEB′=100°,
由折叠得:
∠2=∠FEB′∠BEB′=50°,
故选:A.
7.解:过点E作EM∥AB,如图:
∵AB∥CD,EM∥AB
∴CD∥EM,
∴∠ABE=∠BEM,∠CDE=∠DEM,
∵∠ABF的平分线与∠CDF的平分线相交于点E,
∴∠ABE∠ABF,∠CDE∠CDF,
∴∠BED=∠BEM+∠DEM(∠ABF+∠CDF),
∵∠ABF+∠BFD+∠CDF=360°,
∴∠ABF+∠CDF=360°﹣∠BFD,
∴∠BED(360°﹣∠BFD),
整理得:2∠BED+∠BFD=360°.
故选:C.
8.解:∵BC⊥BD,
∴∠CBD=90°,即∠CBE+∠DBE=90°,
∴∠BCD+∠D=90°,所以③正确;
∵AF∥CD,
∴∠D=∠DBF,
∵BD平分∠EBF,
∴∠DBF=∠DBE,
∴∠CBE=∠BCE,
∵AB∥CE
∴∠ABC=∠BCE,
∴∠ABC=∠CBE,
∴BC平分∠ABE,所以①正确;
∵BC平分∠ACD,
∴∠ACB=∠BCE,
∴∠ACB=∠CBE,
∴AC∥BE,所以②正确;
当∠DBF=2∠ABC时,3∠ABC=90°,
∴∠ABC=30°,
∴∠DBF=60°,
∵∠DEB=∠ABE=2∠ABC,
而∠D=∠DBE=∠DBF,
∠D≠∠BED,
∴∠DBF≠2∠ABC,
∴∠DBF≠60°.故④错误.
故正确的结论有3个.
故选:B.
二.填空题(共8小题)
9.解:如果两个角是锐角,那么它们的和为钝角.
故答案为:如果两个角是锐角,那么它们的和为钝角.
10.解:如图,
∵a∥b,∠1=80°,
∴∠DCE=∠1=80°,
∴∠ACB=∠DCE=80°,
∵∠2=60°,∠ABC=∠2,
∴∠ABC=60°,
∴∠3=180°﹣∠ACB﹣∠ABC=40°.
故答案为:40°.
11.解:过点E作EF∥CD,如图:
则EF∥CD∥AB,
∴∠FEC=∠DCE=40°,∠BAE=∠FEA
∴∠BAE=∠FEA=90°﹣∠FEC=50°,
∴∠1=180°﹣∠BAE=130°,
故答案为:130°.
12.解:由题意得:DE∥AB,
∴∠ABD=∠EDC=50°,
∵∠DEF=∠EDC+∠DCE=120°,
∴∠DCE=70°,
∴∠ACB=∠DCE=70°,
故答案为:70°.
13.解:过点A作AP∥l1,
∴∠PAD=∠1=50°,
∵l1∥l2,
∴AP∥l2,
∴∠PAQ=∠2=25°,
∴∠DAQ=∠DAP+∠PAQ=50°+25°=75°,
∵AQ平分∠DAC,
∴∠CAQ=∠DAQ=75°,
∵AP∥l2,
∴∠3=∠CAP=∠PAQ+∠CAQ=25°+75°=100°,
故答案为:100.
14.解:过点B作BF∥AE,如图,
∵CD∥AE,
∴BF∥CD,
∴∠BCD+∠CBF=180°,
∵AB⊥AE,
∴AB⊥BF,
∴∠ABF=90°,
∠ABC+∠BCD=∠ABF+∠CBF+∠BCD=90°+180°=270°.
故答案为:270.
15.解:∵四边形ABCD是长方形,
∴∠D=90°,
∴∠PED=90°﹣∠1=90°﹣65°=25°,
∵∠FEG=90°,
∴∠DEF=∠PED+∠FEG=115°,
∵AD∥BC,
∴∠2=∠DEF=115°.
故答案为:115°.
16.解:如图,过F作FH∥AB,
∵AB∥CD,
∴FH∥AB∥CD,
∵∠DCE的角平分线CG的反向延长线和∠ABE的角平分线BF交于点F,
∴可设∠ABF=∠EBF=α=∠BFH,∠DCG=∠ECG=β=∠CFH,
∴∠ECF=180°﹣β,∠BFC=∠BFH﹣∠CFH=α﹣β,
∴四边形BFCE中,∠E+∠BFC=360°﹣α﹣(180°﹣β)=180°﹣(α﹣β)=180°﹣∠BFC,
即∠E+2∠BFC=180°,①
又∵∠E﹣∠BFC=60°,
∴∠BFC=∠E﹣60°,②
∴由①②可得,∠E+2(∠E﹣60°)=180°,
解得∠E=100°,
故答案为:100°.
三.解答题(共6小题)
17.证明:∵∠1=∠2,
∴AD∥BE,
∴∠D=∠DBE,
∵∠3=∠D,
∴∠DBE=∠3,
∴BD∥CE.
18.证明:∵EF∥CD(已知),
∴∠BEF=∠BCD(两直线平行,同位角相等),
∵∠B=∠ADG,
∴BC∥DG(同位角互补,两直线平行),
∴∠CDG=∠BCD(两直线平行,内错角相等),
∴∠BEF=∠CDG(等量代换);
故答案为:∠BCD,两直线平行,同位角相等;DG,同位角互补,两直线平行;∠BCD,两直线平行,内错角相等,等量代换.
19.证明:∵∠1=∠2(已知),
又∵∠1=∠3对顶角相等,
∴∠2=∠3(等量代换),
∴AE∥FD (同位角相等,两直线平行),
∴∠A=∠BFD (两直线平行,同位角相等).
∵∠A=∠D(已知),
∴∠D=∠BFD(等量代换),
∴AB∥CD (内错角相等,两直线平行).
∴∠B=∠C (两直线平行,内错角相等).
故答案为:对顶角相等;∠3;同位角相等,两直线平行;两直线平行,同位角相等;∠BFD;AB,内错角相等,两直线平行;两直线平行,内错角相等.
20.解:∵∠CED=∠GHD,
∴CE∥GF,
∴∠C=∠FGD,
∵∠C=∠EFG,
∴∠FGD=∠EFG,
∴AB∥CD,
∴∠AED+∠D=180°,
∵∠D=30°,
∴∠AED=180°﹣30°=150°.
21.证明:(1)∵∠AFD=∠4,∠3=∠4,
∴∠AFD=∠3,
∵∠B=180°﹣∠1﹣∠3,∠D=180°﹣∠2﹣∠AFD,
又∠1=∠2,
∴∠B=∠D;
(2)∵AB∥CD,
∴∠B+∠BCD=180°,
∵∠B=∠D.
∴∠BCD+∠D=180°,
∴AD∥BE.
22.解:(1)∵AM∥BN,
∴∠A+∠ABN=180°.
∵∠A=60°,
∴∠ABN=120°.
∵BC,BD分别平分∠ABP,∠PBN,
∴∠ABP=2∠CBP,∠PBN=2∠DBP,
∴2∠CBP+2∠DBP=120°,
∴∠CBD=∠CBP+∠DBP=60°,
故答案为:120°,60°;
(2)∠APB与∠ADB之间的数量关系不变,∠APB=2∠ADB;
理由:∵AM∥BN,
∴∠APB=∠PBN,∠ADB=∠DBN.
又∵BD平分∠PBN,
∴∠PBN=2∠DBN
,∴∠APB=2∠ADB;
(3)∵AM∥BN,
∴∠ACB=∠CBN.
∵∠ACB=∠ABD,
∴∠CBN=∠ABD,即∠ABC+∠CBD=∠CBD+∠DBN,
∴∠ABC=∠DBN.
∵BC,BD分别平分∠ABP,∠PBN,
∴.
一.选择题(共8小题)
1.观察下列命题:
(1)如果a<0,b>0,那么a+b<0;
(2)直角都相等;
(3)同角的补角相等;
(4)如果两条直线被第三条直线所截,那么同位角相等.
其中真命题的个数是( )
A.0 B.1 C.2 D.3
2.如图,a∥b,∠1=42°,则∠2的度数为( )
A.48° B.42° C.138° D.52°
3.如图,直线a∥b,直线AB⊥AC,若∠1=50°,则∠2=( )
A.30° B.40° C.45° D.50°
4.如图,将三角尺的直角顶点放在直尺的一边上,若∠1=60°15′,则∠2的大小为( )
A.60°15′ B.39°45′ C.29°85′ D.29°45′
5.如图,将直尺与含45°角的直角三角形叠放在一起,若∠2=35°,则∠1的度数为( )
A.35° B.45° C.55° D.65°
6.如图,纸片的边缘AB,CD互相平行,将纸片沿EF折叠,使得点B,D分别落在点B',D'处.若∠1=80°,则∠2的度数是( )
A.50° B.60° C.70° D.80°
7.如图,已知AB∥CD,BE,DE分别平分∠ABF和∠CDF,且交于点E,则( )
A.∠E=∠F B.∠E+∠F=180°
C.2∠E+∠F=360° D.2∠E﹣∠F=180°
8.如图,AF∥CD,BC平分∠ACD,BD平分∠EBF,且BC⊥BD,下列结论:
①BC平分∠ABE;②AC∥BE;
③∠BCD+∠D=90°;
④∠DBF=60°.
其中正确的个数是( )
A.4个 B.3个 C.2个 D.1个
二.填空题(共8小题)
9.将命题“两个锐角的和是钝角”改写成“如果……那么……”的形式是 .
10.如图,已知直线a∥b,∠1=80°,∠2=60°,则∠3= .
11.如图,直线AB∥CD,∠C=40°,∠E为直角,则∠1= .
12.如图为某椅子的侧面图,∠DEF=120°.DE与地面平行,∠ABD=50°,则∠ACB= .
13.如图,直线l1∥l2,AQ平分∠DAC,∠1=50°,∠2=25°,则∠3= °.
14.生活中常见一种折叠拦道闸,如图1所示.若想求解某些特殊状态下的角度,需将其抽象为几何图形,如图2所示,BA垂直于地面AE于A,CD平行于地面AE,则∠ABC+∠BCD= °.
15.如图,含有30°角的直角三角板的两个顶点E、F放在一个长方形的对边上,点E为直角顶点,∠EFG=30°,延长EG交CD于点P,如果∠1=65°,那么∠2的度数是 .
16.如图,AB∥CD,∠DCE的角平分线CG的反向延长线和∠ABE的角平分线BF交于点F,∠E﹣∠F=60°,则∠E= .
三.解答题(共6小题)
17.如图,A、B、C三点在同一直线上,∠1=∠2,∠3=∠D.求证:BD∥CE.
18.如图,已知EF∥CD,数学课上,老师请同学们根据图形特征添加一个关于角的条件,使得∠BEF=∠CDG,并给出证明过程.
小明添加的条件:∠B=∠ADG.
请你帮小明将下面的证明过程补充完整.
证明:∵EF∥CD( )
∴∠BEF= ( )
∵∠B=∠ADG(添加条件)
∴BC∥ ( )
∴∠CDG= ( )
∴∠BEF=∠CDG ( ).
19.请把以下证明过程补充完整,并在下面的括号内填上推理理由:
已知:如图,∠1=∠2,∠A=∠D.
求证:∠B=∠C
证明:∵∠1=∠2,(已知)
又:∵∠1=∠3,
∴∠2= ,(等量代换)
∴AE∥FD
∴∠A=∠BFD
∵∠A=∠D(已知)
∴∠D= (等量代换)
∴ ∥CD
∴∠B=∠C .
20.如图,已知点E、F在直线AB上,点G在线段CD上,ED与FG相交于点H,且∠C=∠EFG,∠CED=∠GHD,∠D=30°.求∠AED的度数.
21.如图,AB∥CD,E是BC的延长线上的一点,AE交CD于点F,∠1=∠2,∠3=∠4.求证:
(1)∠B=∠D;
(2)AD∥BE.
22.如图,已知AM∥BN,∠A=60°,P是射线AM上一动点(与点A不重合),BC,BD分别平分∠ABP和∠PBN,交射线AM于点C,D.
(1)求∠ABN和∠CBD的度数;
(2)当点P运动时,∠APB与∠ADB之间的数量关系是否随之发生变化?若不变,请写出它们之间的关系,并说明理由;若变化,请写出变化规律;
(3)当点P运动到使∠ACB=∠ABD时,求∠ABC的度数.
参考答案
一.选择题(共8小题)
1.解:(1)如果a<0,b>0,那么a+b<0当a=﹣1,b=2时错误,为假命题;
(2)直角都相等,正确,为真命题;
(3)同角的补角相等,正确,为真命题;
(4)如果两条平行直线被第三条直线所截,那么同位角相等,故错误,为假命题,
故选:C.
2.解:∵∠1=∠3=42°,a∥b,
∴∠2=∠3=42°,
故选:B.
3.解:∵直线a∥b,∠1=50°,
∴∠1=∠3=50°,
∵直线AB⊥AC,
∴∠2+∠3=90°.
∴∠2=40°.
故选:B.
4.解:如图,
由直尺两边平行,可得:∠1=∠3=60°15',
∴∠2=90°﹣∠3=90°﹣60°15'=29°45',
故选:D.
5.解:如图,
∵∠ACB=90°,∠2=35°,
∴∠3=90°﹣∠2=90°﹣35°=55°,
∵直尺对边平行,
∴∠1=∠3=55°.
故选:C.
6.解:∵AB∥CD,
∴∠1=∠AEB′=80°,
∴∠BEB′=180°﹣∠AEB′=100°,
由折叠得:
∠2=∠FEB′∠BEB′=50°,
故选:A.
7.解:过点E作EM∥AB,如图:
∵AB∥CD,EM∥AB
∴CD∥EM,
∴∠ABE=∠BEM,∠CDE=∠DEM,
∵∠ABF的平分线与∠CDF的平分线相交于点E,
∴∠ABE∠ABF,∠CDE∠CDF,
∴∠BED=∠BEM+∠DEM(∠ABF+∠CDF),
∵∠ABF+∠BFD+∠CDF=360°,
∴∠ABF+∠CDF=360°﹣∠BFD,
∴∠BED(360°﹣∠BFD),
整理得:2∠BED+∠BFD=360°.
故选:C.
8.解:∵BC⊥BD,
∴∠CBD=90°,即∠CBE+∠DBE=90°,
∴∠BCD+∠D=90°,所以③正确;
∵AF∥CD,
∴∠D=∠DBF,
∵BD平分∠EBF,
∴∠DBF=∠DBE,
∴∠CBE=∠BCE,
∵AB∥CE
∴∠ABC=∠BCE,
∴∠ABC=∠CBE,
∴BC平分∠ABE,所以①正确;
∵BC平分∠ACD,
∴∠ACB=∠BCE,
∴∠ACB=∠CBE,
∴AC∥BE,所以②正确;
当∠DBF=2∠ABC时,3∠ABC=90°,
∴∠ABC=30°,
∴∠DBF=60°,
∵∠DEB=∠ABE=2∠ABC,
而∠D=∠DBE=∠DBF,
∠D≠∠BED,
∴∠DBF≠2∠ABC,
∴∠DBF≠60°.故④错误.
故正确的结论有3个.
故选:B.
二.填空题(共8小题)
9.解:如果两个角是锐角,那么它们的和为钝角.
故答案为:如果两个角是锐角,那么它们的和为钝角.
10.解:如图,
∵a∥b,∠1=80°,
∴∠DCE=∠1=80°,
∴∠ACB=∠DCE=80°,
∵∠2=60°,∠ABC=∠2,
∴∠ABC=60°,
∴∠3=180°﹣∠ACB﹣∠ABC=40°.
故答案为:40°.
11.解:过点E作EF∥CD,如图:
则EF∥CD∥AB,
∴∠FEC=∠DCE=40°,∠BAE=∠FEA
∴∠BAE=∠FEA=90°﹣∠FEC=50°,
∴∠1=180°﹣∠BAE=130°,
故答案为:130°.
12.解:由题意得:DE∥AB,
∴∠ABD=∠EDC=50°,
∵∠DEF=∠EDC+∠DCE=120°,
∴∠DCE=70°,
∴∠ACB=∠DCE=70°,
故答案为:70°.
13.解:过点A作AP∥l1,
∴∠PAD=∠1=50°,
∵l1∥l2,
∴AP∥l2,
∴∠PAQ=∠2=25°,
∴∠DAQ=∠DAP+∠PAQ=50°+25°=75°,
∵AQ平分∠DAC,
∴∠CAQ=∠DAQ=75°,
∵AP∥l2,
∴∠3=∠CAP=∠PAQ+∠CAQ=25°+75°=100°,
故答案为:100.
14.解:过点B作BF∥AE,如图,
∵CD∥AE,
∴BF∥CD,
∴∠BCD+∠CBF=180°,
∵AB⊥AE,
∴AB⊥BF,
∴∠ABF=90°,
∠ABC+∠BCD=∠ABF+∠CBF+∠BCD=90°+180°=270°.
故答案为:270.
15.解:∵四边形ABCD是长方形,
∴∠D=90°,
∴∠PED=90°﹣∠1=90°﹣65°=25°,
∵∠FEG=90°,
∴∠DEF=∠PED+∠FEG=115°,
∵AD∥BC,
∴∠2=∠DEF=115°.
故答案为:115°.
16.解:如图,过F作FH∥AB,
∵AB∥CD,
∴FH∥AB∥CD,
∵∠DCE的角平分线CG的反向延长线和∠ABE的角平分线BF交于点F,
∴可设∠ABF=∠EBF=α=∠BFH,∠DCG=∠ECG=β=∠CFH,
∴∠ECF=180°﹣β,∠BFC=∠BFH﹣∠CFH=α﹣β,
∴四边形BFCE中,∠E+∠BFC=360°﹣α﹣(180°﹣β)=180°﹣(α﹣β)=180°﹣∠BFC,
即∠E+2∠BFC=180°,①
又∵∠E﹣∠BFC=60°,
∴∠BFC=∠E﹣60°,②
∴由①②可得,∠E+2(∠E﹣60°)=180°,
解得∠E=100°,
故答案为:100°.
三.解答题(共6小题)
17.证明:∵∠1=∠2,
∴AD∥BE,
∴∠D=∠DBE,
∵∠3=∠D,
∴∠DBE=∠3,
∴BD∥CE.
18.证明:∵EF∥CD(已知),
∴∠BEF=∠BCD(两直线平行,同位角相等),
∵∠B=∠ADG,
∴BC∥DG(同位角互补,两直线平行),
∴∠CDG=∠BCD(两直线平行,内错角相等),
∴∠BEF=∠CDG(等量代换);
故答案为:∠BCD,两直线平行,同位角相等;DG,同位角互补,两直线平行;∠BCD,两直线平行,内错角相等,等量代换.
19.证明:∵∠1=∠2(已知),
又∵∠1=∠3对顶角相等,
∴∠2=∠3(等量代换),
∴AE∥FD (同位角相等,两直线平行),
∴∠A=∠BFD (两直线平行,同位角相等).
∵∠A=∠D(已知),
∴∠D=∠BFD(等量代换),
∴AB∥CD (内错角相等,两直线平行).
∴∠B=∠C (两直线平行,内错角相等).
故答案为:对顶角相等;∠3;同位角相等,两直线平行;两直线平行,同位角相等;∠BFD;AB,内错角相等,两直线平行;两直线平行,内错角相等.
20.解:∵∠CED=∠GHD,
∴CE∥GF,
∴∠C=∠FGD,
∵∠C=∠EFG,
∴∠FGD=∠EFG,
∴AB∥CD,
∴∠AED+∠D=180°,
∵∠D=30°,
∴∠AED=180°﹣30°=150°.
21.证明:(1)∵∠AFD=∠4,∠3=∠4,
∴∠AFD=∠3,
∵∠B=180°﹣∠1﹣∠3,∠D=180°﹣∠2﹣∠AFD,
又∠1=∠2,
∴∠B=∠D;
(2)∵AB∥CD,
∴∠B+∠BCD=180°,
∵∠B=∠D.
∴∠BCD+∠D=180°,
∴AD∥BE.
22.解:(1)∵AM∥BN,
∴∠A+∠ABN=180°.
∵∠A=60°,
∴∠ABN=120°.
∵BC,BD分别平分∠ABP,∠PBN,
∴∠ABP=2∠CBP,∠PBN=2∠DBP,
∴2∠CBP+2∠DBP=120°,
∴∠CBD=∠CBP+∠DBP=60°,
故答案为:120°,60°;
(2)∠APB与∠ADB之间的数量关系不变,∠APB=2∠ADB;
理由:∵AM∥BN,
∴∠APB=∠PBN,∠ADB=∠DBN.
又∵BD平分∠PBN,
∴∠PBN=2∠DBN
,∴∠APB=2∠ADB;
(3)∵AM∥BN,
∴∠ACB=∠CBN.
∵∠ACB=∠ABD,
∴∠CBN=∠ABD,即∠ABC+∠CBD=∠CBD+∠DBN,
∴∠ABC=∠DBN.
∵BC,BD分别平分∠ABP,∠PBN,
∴.
