2023-2024学年人教A版高一上学期真题汇编:函数概念与性质(含答案)
文档属性
| 名称 | 2023-2024学年人教A版高一上学期真题汇编:函数概念与性质(含答案) | 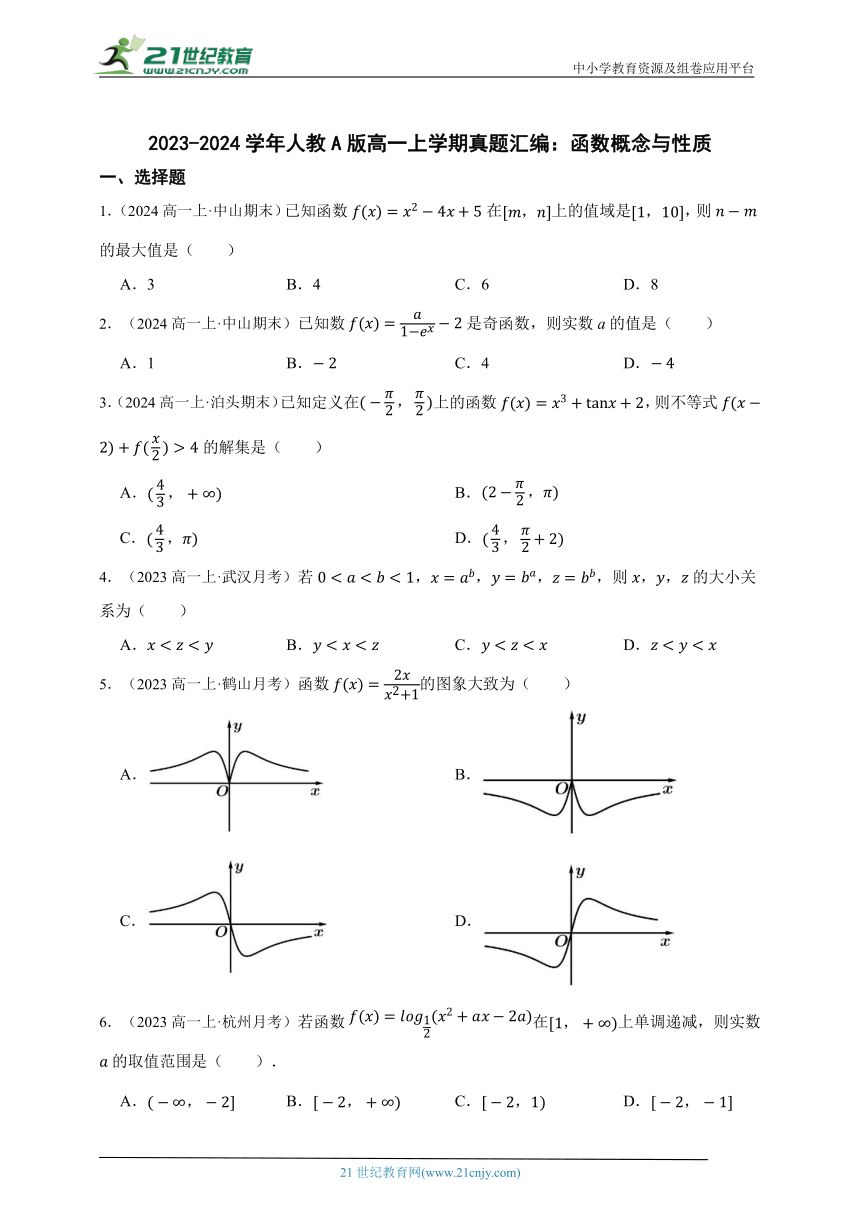 | |
| 格式 | docx | ||
| 文件大小 | 374.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-18 16:19:32 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2023-2024学年人教A版高一上学期真题汇编:函数概念与性质
一、选择题
1.(2024高一上·中山期末)已知函数在上的值域是,则的最大值是( )
A.3 B.4 C.6 D.8
2.(2024高一上·中山期末)已知数是奇函数,则实数a的值是( )
A.1 B. C.4 D.
3.(2024高一上·泊头期末)已知定义在上的函数,则不等式的解集是( )
A. B.
C. D.
4.(2023高一上·武汉月考)若,,,,则,,的大小关系为( )
A. B. C. D.
5.(2023高一上·鹤山月考)函数的图象大致为( )
A. B.
C. D.
6.(2023高一上·杭州月考)若函数在上单调递减,则实数的取值范围是( ).
A. B. C. D.
7.(2023高一上·杭州月考)若奇函数和偶函数满足,则( )
A. B. C. D.
8.(2023高一上·齐齐哈尔月考)集合的真子集个数为( )
A.7 B.8 C.15 D.16
二、多项选择题
9.(2024高一上·中山期末)给定函数,则( )
A.的图象关于原点对称 B.的值域是
C.在区间上是增函数 D.有三个零点
10.(2024高一上·中山期末)下列函数中,既是奇函数,又是R上的增函数的是( )
A. B. C. D.
11.(2024高一上·泊头期末)下列说法正确的是( )
A.若幂函数的图象经过点,则函数的解析式为
B.若函数,则在区间上单调递减
C.若正实数m,n满足,则
D.若函数,则对任意,,且,有
12.(2024高一上·中山期末)设偶函数的定义域为,且满足,对于任意,都有二成立则( )
A.不等式的解集为
B.不等式的解集为
C.不等式的解集为
D.不等式的解集为
三、填空题
13.(2023高一上·浦东月考)已知幂函数在上是严格减函数,则 .
14.(2023高一上·浦东月考)若函数为偶函数且非奇函数,则实数的取值范围为 .
15.(2023高一上·浦东月考)已知定义在上的函数,其中,如果函数与函数的值域相同,则的取值范围是 .
16.(2023高一上·鹤山月考)若函数 满足对任意的实数 都有 成立,则实数 的取值范围是 .
四、解答题
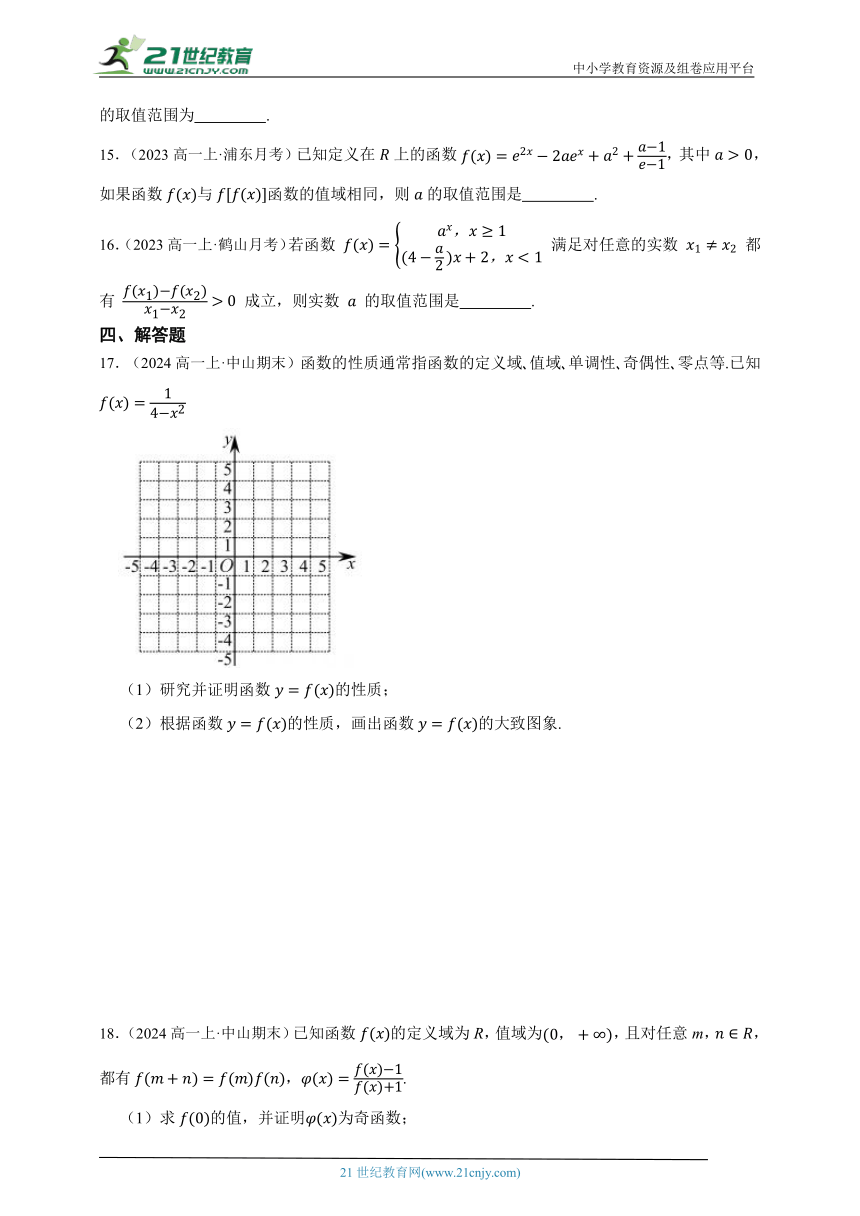
17.(2024高一上·中山期末)函数的性质通常指函数的定义域 值域 单调性 奇偶性 零点等.已知
(1)研究并证明函数的性质;
(2)根据函数的性质,画出函数的大致图象.
18.(2024高一上·中山期末)已知函数的定义域为R,值域为,且对任意m,,都有,.
(1)求的值,并证明为奇函数;
(2)当时,,且,证明为R上的增函数,并解不等式
19.(2023高一上·肇东期末)已知是定义在R上的奇函数,且当时,.
(1)求的值;
(2)求函数的解析式.
20.(2023高一上·浦东月考)近来,国内多个城市纷纷加码布局“夜经济”,以满足不同层次的多元消费,并拉动就业、带动创业,进而提升区域经济发展活力,某夜市的一位工艺品售卖者,通过对每天销售情况的调查发现:该工艺品在过去的一个月内(以30天计),每件的销售价格(单位:元)与时间(单位:天)的函数关系近似满足。且销售量(单位:件)与时间(单位:天)的部分数据如下表所示
x 10 15 20 25 30
Q(x) 50 55 60 55 50
(1)给出以下四个函数模型:①;②;③;④。请你根据上表中的数据,从中选择你认为最合适的一种函数模型来描述日销售量与时间的变化关系,并求出该函数的解析式及定义域
(2)设该工艺品的日销售收入为(单位:元),求的最小值。
21.(2023高一上·浦东月考)已知函数是定义在上的奇函数,且当时,
(1)求证:在定义域内是严格减函数
(2)若对恒成立,求实数的取值范围。
22.(2023高一上·杭州月考)已知函数是奇函数,且.
(1)求实数、的值;
(2)求函数在的值域;
(3)若,求实数的取值范围.
答案解析部分
1.【答案】C
2.【答案】C
3.【答案】C
4.【答案】A
5.【答案】D
6.【答案】C
7.【答案】D
8.【答案】A
9.【答案】A,B
10.【答案】B,C
11.【答案】A,C,D
12.【答案】A,C
13.【答案】
14.【答案】
15.【答案】
16.【答案】[4,8)
17.【答案】(1)解:①函数的定义域为,
②因为定义域关于原点对称,又,所以是偶函数;
③任取,且,
则,
因为,所以,
又因为,所以,所以,即,
所以函数在区间上单调递增,
同理可得在区间上单调递增,
又是偶函数,则在和上单调递减;
④令,则,所以;
⑤函数没有零点;
(2)解:根据函数的性质,作出其图象如图所示:
18.【答案】(1)解:令,得,
又函数的值域为.
,
为奇函数
(2)解:任取.
.
.
当时,.
又函数的值域为,
,即为上的增函数.
由,即,化简得.
.
又为上的增函数,,故的解集为.
19.【答案】(1)解:因为,
又由函数是上的奇函数,则.
(2)解:因为是奇函数,所以
当时,则,则,
所以函数的解析式为 .
20.【答案】(1)解:由表格数据知,当时间变换时,先增后减,而①③④都是单调函数
所以选择模型②,
由,可得,解得
由,解得
所以日销售量与时间的变化的关系式为
(2)解:由(1)知:
所以
即
当时,
由基本不等式,可得,当且仅当时,即时等号成立
当时,为减函数
所以函数的最小值为
综上,当时,函数取得最小值441.
21.【答案】(1)解:设,
则在内是严格减函数,又奇函数对称区间上的单调性相同
则在定义域内是严格减函数
(2)解:
当时,
则实数的取值范围为
22.【答案】(1)解:函数为奇函数,
所以,即,
则,所以,所以,
当时无意义,
当时,则,解得,
所以函数的定义域为,且,
符合题意,
又,所以,则,所以,
综上可得、.
(2)解:由(1)可得,
因为在上单调递增,在定义域上单调递减,
所以在上单调递减,且的值域为,
当,则,又,
所以函数在的值域为.
(3)解:由(1)(2)可知为定义在上单调递减奇函数,
不等式,即,
等价于,解得,
所以实数的取值范围为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2023-2024学年人教A版高一上学期真题汇编:函数概念与性质
一、选择题
1.(2024高一上·中山期末)已知函数在上的值域是,则的最大值是( )
A.3 B.4 C.6 D.8
2.(2024高一上·中山期末)已知数是奇函数,则实数a的值是( )
A.1 B. C.4 D.
3.(2024高一上·泊头期末)已知定义在上的函数,则不等式的解集是( )
A. B.
C. D.
4.(2023高一上·武汉月考)若,,,,则,,的大小关系为( )
A. B. C. D.
5.(2023高一上·鹤山月考)函数的图象大致为( )
A. B.
C. D.
6.(2023高一上·杭州月考)若函数在上单调递减,则实数的取值范围是( ).
A. B. C. D.
7.(2023高一上·杭州月考)若奇函数和偶函数满足,则( )
A. B. C. D.
8.(2023高一上·齐齐哈尔月考)集合的真子集个数为( )
A.7 B.8 C.15 D.16
二、多项选择题
9.(2024高一上·中山期末)给定函数,则( )
A.的图象关于原点对称 B.的值域是
C.在区间上是增函数 D.有三个零点
10.(2024高一上·中山期末)下列函数中,既是奇函数,又是R上的增函数的是( )
A. B. C. D.
11.(2024高一上·泊头期末)下列说法正确的是( )
A.若幂函数的图象经过点,则函数的解析式为
B.若函数,则在区间上单调递减
C.若正实数m,n满足,则
D.若函数,则对任意,,且,有
12.(2024高一上·中山期末)设偶函数的定义域为,且满足,对于任意,都有二成立则( )
A.不等式的解集为
B.不等式的解集为
C.不等式的解集为
D.不等式的解集为
三、填空题
13.(2023高一上·浦东月考)已知幂函数在上是严格减函数,则 .
14.(2023高一上·浦东月考)若函数为偶函数且非奇函数,则实数的取值范围为 .
15.(2023高一上·浦东月考)已知定义在上的函数,其中,如果函数与函数的值域相同,则的取值范围是 .
16.(2023高一上·鹤山月考)若函数 满足对任意的实数 都有 成立,则实数 的取值范围是 .
四、解答题
17.(2024高一上·中山期末)函数的性质通常指函数的定义域 值域 单调性 奇偶性 零点等.已知
(1)研究并证明函数的性质;
(2)根据函数的性质,画出函数的大致图象.
18.(2024高一上·中山期末)已知函数的定义域为R,值域为,且对任意m,,都有,.
(1)求的值,并证明为奇函数;
(2)当时,,且,证明为R上的增函数,并解不等式
19.(2023高一上·肇东期末)已知是定义在R上的奇函数,且当时,.
(1)求的值;
(2)求函数的解析式.
20.(2023高一上·浦东月考)近来,国内多个城市纷纷加码布局“夜经济”,以满足不同层次的多元消费,并拉动就业、带动创业,进而提升区域经济发展活力,某夜市的一位工艺品售卖者,通过对每天销售情况的调查发现:该工艺品在过去的一个月内(以30天计),每件的销售价格(单位:元)与时间(单位:天)的函数关系近似满足。且销售量(单位:件)与时间(单位:天)的部分数据如下表所示
x 10 15 20 25 30
Q(x) 50 55 60 55 50
(1)给出以下四个函数模型:①;②;③;④。请你根据上表中的数据,从中选择你认为最合适的一种函数模型来描述日销售量与时间的变化关系,并求出该函数的解析式及定义域
(2)设该工艺品的日销售收入为(单位:元),求的最小值。
21.(2023高一上·浦东月考)已知函数是定义在上的奇函数,且当时,
(1)求证:在定义域内是严格减函数
(2)若对恒成立,求实数的取值范围。
22.(2023高一上·杭州月考)已知函数是奇函数,且.
(1)求实数、的值;
(2)求函数在的值域;
(3)若,求实数的取值范围.
答案解析部分
1.【答案】C
2.【答案】C
3.【答案】C
4.【答案】A
5.【答案】D
6.【答案】C
7.【答案】D
8.【答案】A
9.【答案】A,B
10.【答案】B,C
11.【答案】A,C,D
12.【答案】A,C
13.【答案】
14.【答案】
15.【答案】
16.【答案】[4,8)
17.【答案】(1)解:①函数的定义域为,
②因为定义域关于原点对称,又,所以是偶函数;
③任取,且,
则,
因为,所以,
又因为,所以,所以,即,
所以函数在区间上单调递增,
同理可得在区间上单调递增,
又是偶函数,则在和上单调递减;
④令,则,所以;
⑤函数没有零点;
(2)解:根据函数的性质,作出其图象如图所示:
18.【答案】(1)解:令,得,
又函数的值域为.
,
为奇函数
(2)解:任取.
.
.
当时,.
又函数的值域为,
,即为上的增函数.
由,即,化简得.
.
又为上的增函数,,故的解集为.
19.【答案】(1)解:因为,
又由函数是上的奇函数,则.
(2)解:因为是奇函数,所以
当时,则,则,
所以函数的解析式为 .
20.【答案】(1)解:由表格数据知,当时间变换时,先增后减,而①③④都是单调函数
所以选择模型②,
由,可得,解得
由,解得
所以日销售量与时间的变化的关系式为
(2)解:由(1)知:
所以
即
当时,
由基本不等式,可得,当且仅当时,即时等号成立
当时,为减函数
所以函数的最小值为
综上,当时,函数取得最小值441.
21.【答案】(1)解:设,
则在内是严格减函数,又奇函数对称区间上的单调性相同
则在定义域内是严格减函数
(2)解:
当时,
则实数的取值范围为
22.【答案】(1)解:函数为奇函数,
所以,即,
则,所以,所以,
当时无意义,
当时,则,解得,
所以函数的定义域为,且,
符合题意,
又,所以,则,所以,
综上可得、.
(2)解:由(1)可得,
因为在上单调递增,在定义域上单调递减,
所以在上单调递减,且的值域为,
当,则,又,
所以函数在的值域为.
(3)解:由(1)(2)可知为定义在上单调递减奇函数,
不等式,即,
等价于,解得,
所以实数的取值范围为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
