2023-2024学年数学九年级下册人教版第二十八章锐角三角函数试卷(含解析)
文档属性
| 名称 | 2023-2024学年数学九年级下册人教版第二十八章锐角三角函数试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 510.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-16 17:26:51 | ||
图片预览


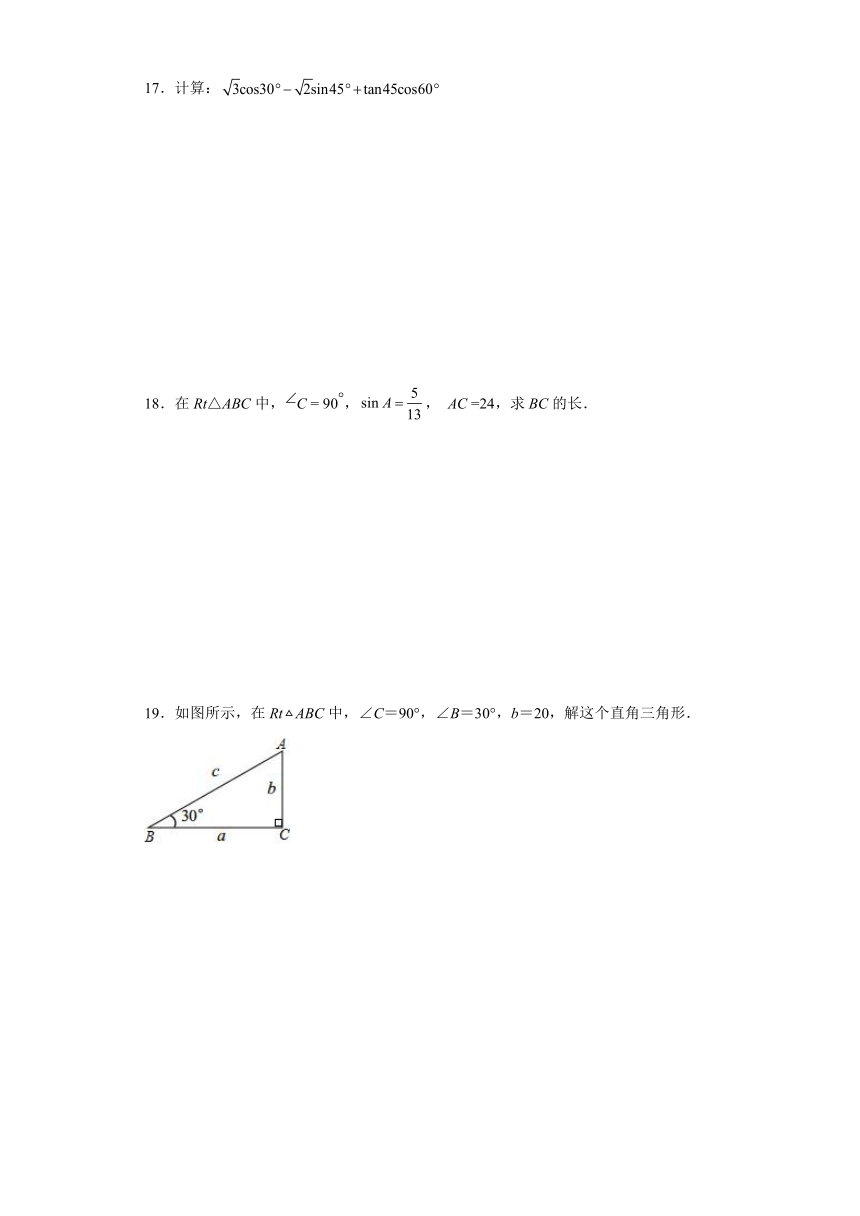
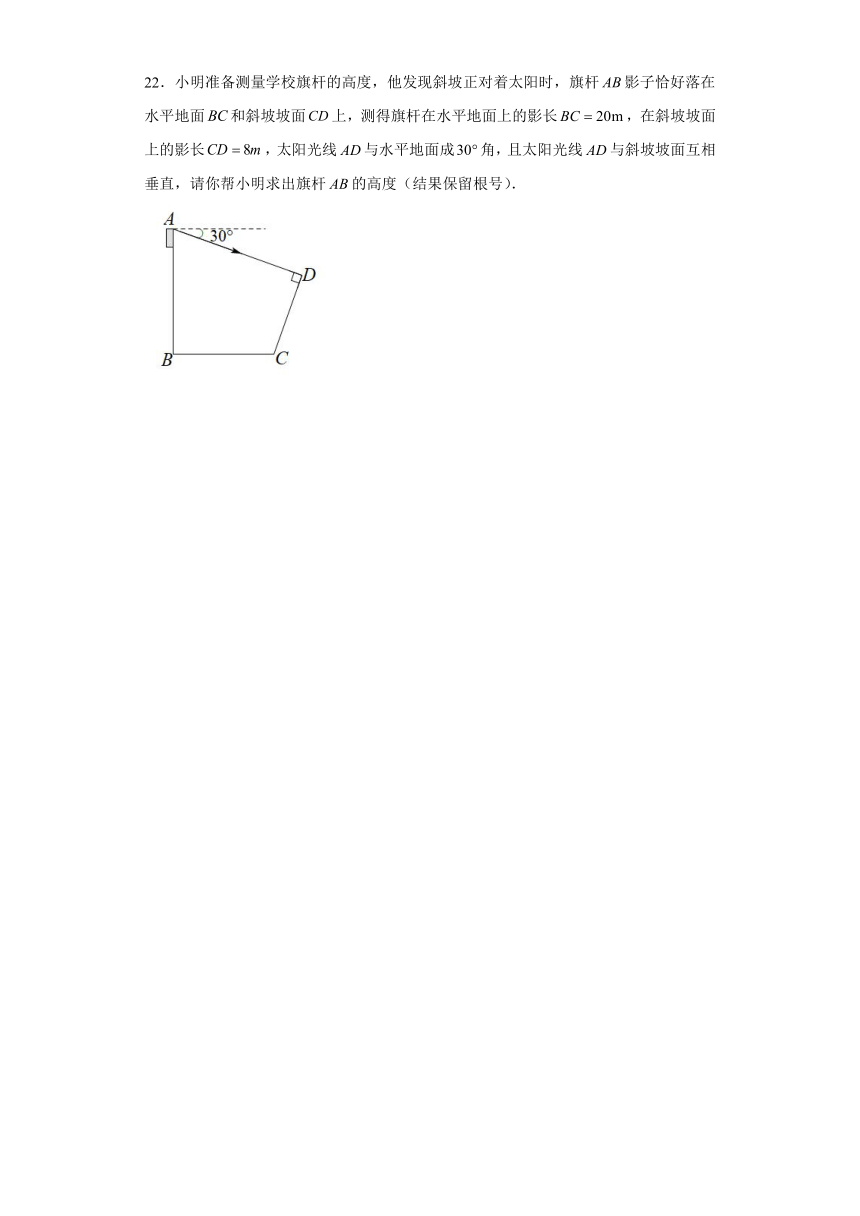
文档简介
2023-2024学年数学九年级下册人教版第二十八章锐角三角函数
一、单选题
1. 的值是( )
A. B. C.1 D.
2.若,则锐角的度数为( )
A. B. C. D.
3.如图,在边长为1的小正方形组成的网格中,的三个顶点均在格点上,则( )
A. B. C. D.
4.在中,,,,则的值为( )
A. B. C. D.
5.李红同学遇到了这样一道题:,你猜想锐角α的度数应是( )
A. B. C. D.
6.在中,若,,则是( )
A.等腰三角形 B.等边三角形 C.直角三角形 D.等腰直角三角形
7.如图,在地面上的点A处测得树顶B的仰角为a,米,则树高为( )
A.米 B.米 C.米 D. 米
8.如图,在矩形中,,,对角线的垂直平分线分别交于点,则的长为( )
A. B. C. D.
二、填空题
9.,则 .
10.一个斜坡的坡角为度,它的坡比 .
11.在Rt△ABC中,∠C=90°,AB=5,BC=3,则sinA= .
12.公园有一个亭子的底面是边长为2m的正六边形,这个正六边形底面的面积是 m2.
13.在中,,,,则AC的长是 .
14.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,tan∠DCB=,AC=12,则BC= .
15.如图,在4×5的正方形网格中,每个小正方形的边长都是1,△ABC的顶点都在这些小正方形的顶点上,那么sin∠ACB的值为 .
16.如果是锐角,且,那么 度
三、解答题
17.计算:
18.在Rt△ABC中,C = 90,, AC =24,求BC的长.
19.如图所示,在RtABC中,∠C=90°,∠B=30°,b=20,解这个直角三角形.
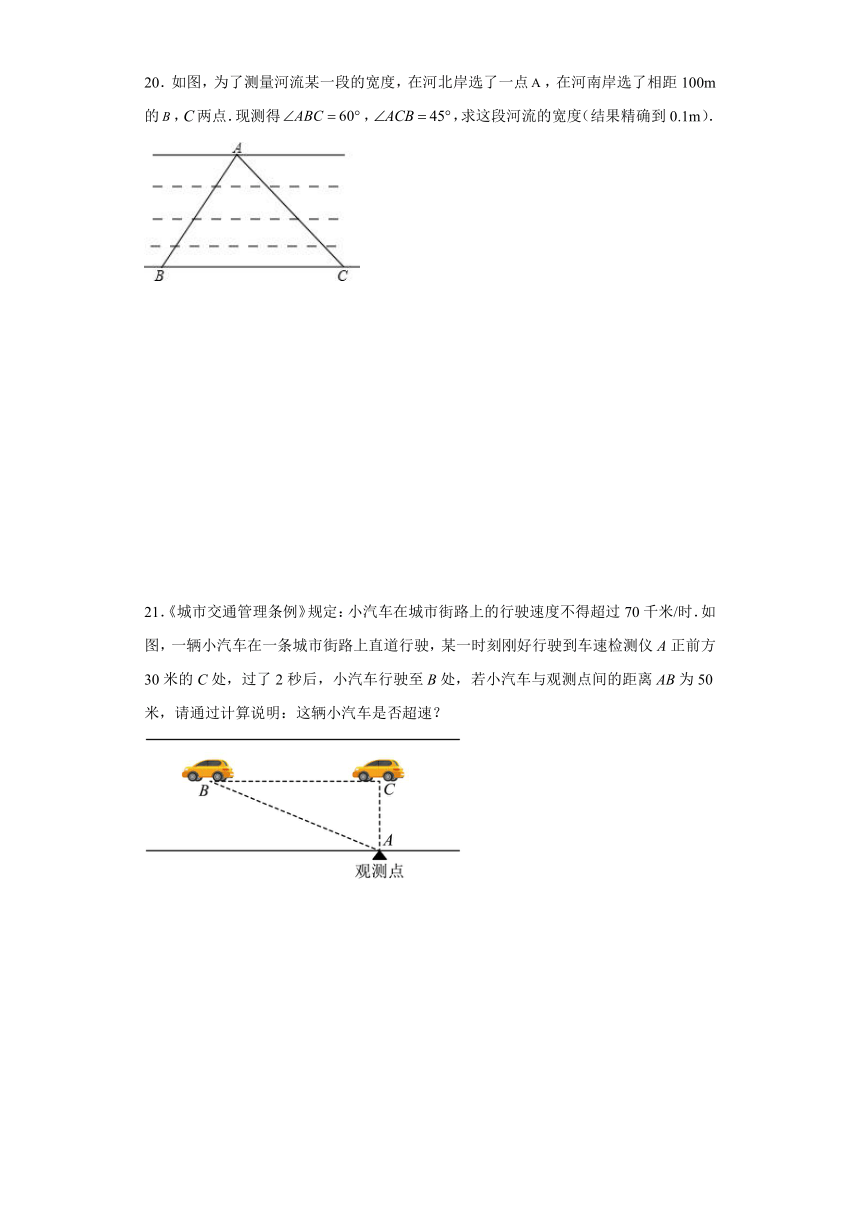
20.如图,为了测量河流某一段的宽度,在河北岸选了一点,在河南岸选了相距100m的,两点.现测得,,求这段河流的宽度(结果精确到0.1m).
21.《城市交通管理条例》规定:小汽车在城市街路上的行驶速度不得超过70千米/时.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到车速检测仪A正前方30米的C处,过了2秒后,小汽车行驶至B处,若小汽车与观测点间的距离AB为50米,请通过计算说明:这辆小汽车是否超速?
22.小明准备测量学校旗杆的高度,他发现斜坡正对着太阳时,旗杆影子恰好落在水平地面和斜坡坡面上,测得旗杆在水平地面上的影长,在斜坡坡面上的影长,太阳光线与水平地面成角,且太阳光线与斜坡坡面互相垂直,请你帮小明求出旗杆的高度(结果保留根号).
参考答案:
1.D
【分析】本题考查了正切.熟练掌握特殊角的正切是解题的关键.
根据,作答即可.
【详解】解:,
故选:D.
2.A
【分析】本题考查了特殊角的三角函数值,解答本题的关键是掌握几个特殊角的三角函数值.并且根据特殊的三角函数值求解.
【详解】为锐角,,
.
故选:A.
3.D
【分析】本题考查了解直角三角形.由三角函数定义即可得出答案.
【详解】解:由图可得:,
∴.
故选:D.
4.B
【分析】根据余弦的定义计算即可.
【详解】解:如图,
∵中,,,,
∴
在中,,
故选B.
【点睛】本题考查的是锐角三角函数的定义,掌握锐角A的邻边b与斜边c的比叫做角A的余弦是解题的关键.
5.D
【分析】根据特殊角的三角函数值求解即可.
【详解】解:
∴
∴
∴.
故选:D.
【点睛】本题考查的是特殊角的三角函数值,熟记特殊角的三角函数值是解题的关键.
6.B
【分析】根据特殊角的三角函数值分别求出、,根据等边三角形的判定定理判断即可.
【详解】解:∵,
∴,
∴是等边三角形
故选:B.
【点睛】本题考查的是特殊角的三角函数值,等边三角形的判定,熟记、、角的各种三角函数值是解题的关键.
7.C
【分析】利用三角函数值中正切,可得到与的关系,计算即可.
【详解】在中, ,
,
故选C.
【点睛】本题考查三角函数值的应用,注意区分三边对应关系.
8.D
【分析】根据题意以及矩形的性质,勾股定理求得,进而根据得出即可求解.
【详解】解:∵四边形是矩形,,,
∴,,
∵对角线的垂直平分线分别交于点,
∴,,
∵,则,
∴,
∴,
解得:,
故选:D
【点睛】本题考查了矩形的性质,正切的定义,勾股定理,垂直平分线的性质,得出是解题的关键.
9.30
【分析】根据特殊角的三角函数值即可求解.
【详解】解:,
,
故答案为:30.
【点睛】本题考查了由三角函数值求锐角,熟练掌握特殊角的三角函数值是解题的关键.
10.
【分析】坡比,即坡面的垂直高度和水平宽度的比,即坡角的正切值,由此即可求解.
【详解】解:如图所示,,,,
∴设,则,
∴,
故答案为:.
【点睛】本题主要考查坡比的概念及计算方法,掌握其概念和计算方法是解题的关键.
11.
【分析】先画出图形,再根据正弦三角函数的定义即可得.
【详解】解:由题意,画出图形如下:
,
,
故答案为:.
【点睛】本题考查了正弦,熟练掌握正弦的概念是解题关键.
12.
【分析】如图,连接正六边形对角顶点交于O点,将正六边形分成6个全等的等边三角形,过O点作AB边垂线于H点,计算出三角形AOB的面积,乘以6即可求出答案.
【详解】解:如图,连接正六边形对角顶点交于O点,过O点作AB边垂线于H点,
易知为等边三角形,,,
,
这个正六边形底面的面积,
故答案为:.
【点睛】本题考查了正六边形面积计算、利用锐角三角函数解直角三角形等知识点,通过作图将正六边形分成6个全等的等边三角形是解题的突破口.
13.9
【分析】首先根据锐角三角函数得出,再将AB的值代入计算即可.
【详解】在Rt△ABC中,.
∵AB=15,
∴,
解得AC=9.
故答案为:9.
【点睛】本题主要考查了解直角三角形的知识,正确的选择锐角三角函数是解题的关键.
14.9
【分析】根据直角三角形的性质、同角的余角相等得到∠BCD=∠A,根据正切的定义计算即可
【详解】解:∵∠ACB=90°,
∴∠A+∠B=90°,
∵CD⊥AB,
∴∠BCD+∠B=90°,
∴∠BCD=∠A,
在Rt△ACB中,
∵tanA=tan∠BCD==,
∴BC=AC=×12=9.
故答案为:9.
【点睛】本题考查了解直角三角形:掌握正切的定义是解题的关键.
15./0.8
【分析】如图,过点A作AH⊥BC于H.利用勾股定理求出AC即可解决问题.
【详解】解:如图,过点A作AH⊥BC于H.
在Rt△ACH中,∵AH=4,CH=3,
∴AC==5,
∴sin∠ACH=,
故答案为:.
【点睛】本题考查了解直角三角形,解题的关键是学会添加常用辅助线,构造直角三角形解决问题.
16.48
【分析】根据锐角三角函数关系:,即可求解.
【详解】∵是锐角,,
又∵,
∴48°.
故答案是48.
【点睛】本题主要考查锐角三角函数的关系,掌握,是解题的关键.
17.1
【分析】直接利用特殊角的三角函数值代入求出答案即可.
【详解】
,
,
.
【点睛】本题考查实数运算,熟记特殊角的三角函数值是解题的关键.
18.10
【分析】根据∠C=90°,,设BC=5x,AB=13x,再根据勾股定理求出AC =12x,求出x的值,再代入BC=5x,进行计算即可.
【详解】解:在Rt△ABC中,C = 90,
∴
设BC=5x,AB=13x.
由勾股定理得AC =12x.
∵AC =24,
∴12x=24 解得x=2
∴BC=5x=10
【点睛】本题考查了解直角三角形和勾股定理的应用,解此题的关键是得出关于x的方程,难度适中.
19.∠A=60°,,c=40
【分析】直角三角形的两个锐角互余,并且Rt△ABC中,∠C=90°则∠A=90-∠B=60°,解直角三角形就是求直角三角形中除直角以外的两锐角,三边中的未知的元素.
【详解】由∠C=90°知,∠A+∠B=90°,而∠B=30°,
∴∠A=90°-30°=60°,
,
∴,
∴c=40,
由勾股定理知,
∴,
解得:.
【点睛】考查了解直角三角形的条件,已知三角形的一边与一个锐角,就可以求出另一个锐角与三角形的另外两边.
20.63.4m
【分析】过A作AD⊥BC于D,根据∠ABC=60°,∠ACB=45°即可求出BD、CD与AD关系,根据BC=100m,可以求得AD的长度.
【详解】解:过A作AD⊥BC于D,
在Rt△ADB中,∠B=60°,
∴∠BAD=30°,
∴BD=AD tan30°=AD,
在Rt△ADC中,∠C=45°,
∴CD=AD,又BC=100m,
∴BD+CD=AD+AD=100.
解得AD≈63.4m.
答:这段河的宽约为63.4米.
【点睛】本题考查了解直角三角形的应用,解题关键是恰当构建直角三角形,利用三角函数求解.
21.这辆小汽车超速了.
【分析】求出BC的距离,根据时间求出速度,从而可知道是否超速.
【详解】解:根据题意:∠ACB= 90°
由勾股定理可得:
BC=米
40米= 0.04千米,
2秒=小时;
0.04÷= 72千米/时> 70千米/时;
所以超速了.
【点睛】本题考查勾股定理的应用,解题的关键是掌握构造直角三角形,确定直角边,斜边即可.
22.
【分析】延长,交于点,在中,由含30°角的直角三角形的性质求出,得出,再由三角函数求出即可.
【详解】解:延长,交于点,如图所示:
根据平行线的性质得:,
∵在中,,
∴,
则,
在中,
,
答:旗杆的高度为.
【点睛】此题考查了解直角三角形的应用、含30°角的直角三角形的性质,由含30°角的直角三角形的性质求出,得出是解决问题的关键.
一、单选题
1. 的值是( )
A. B. C.1 D.
2.若,则锐角的度数为( )
A. B. C. D.
3.如图,在边长为1的小正方形组成的网格中,的三个顶点均在格点上,则( )
A. B. C. D.
4.在中,,,,则的值为( )
A. B. C. D.
5.李红同学遇到了这样一道题:,你猜想锐角α的度数应是( )
A. B. C. D.
6.在中,若,,则是( )
A.等腰三角形 B.等边三角形 C.直角三角形 D.等腰直角三角形
7.如图,在地面上的点A处测得树顶B的仰角为a,米,则树高为( )
A.米 B.米 C.米 D. 米
8.如图,在矩形中,,,对角线的垂直平分线分别交于点,则的长为( )
A. B. C. D.
二、填空题
9.,则 .
10.一个斜坡的坡角为度,它的坡比 .
11.在Rt△ABC中,∠C=90°,AB=5,BC=3,则sinA= .
12.公园有一个亭子的底面是边长为2m的正六边形,这个正六边形底面的面积是 m2.
13.在中,,,,则AC的长是 .
14.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,tan∠DCB=,AC=12,则BC= .
15.如图,在4×5的正方形网格中,每个小正方形的边长都是1,△ABC的顶点都在这些小正方形的顶点上,那么sin∠ACB的值为 .
16.如果是锐角,且,那么 度
三、解答题
17.计算:
18.在Rt△ABC中,C = 90,, AC =24,求BC的长.
19.如图所示,在RtABC中,∠C=90°,∠B=30°,b=20,解这个直角三角形.
20.如图,为了测量河流某一段的宽度,在河北岸选了一点,在河南岸选了相距100m的,两点.现测得,,求这段河流的宽度(结果精确到0.1m).
21.《城市交通管理条例》规定:小汽车在城市街路上的行驶速度不得超过70千米/时.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到车速检测仪A正前方30米的C处,过了2秒后,小汽车行驶至B处,若小汽车与观测点间的距离AB为50米,请通过计算说明:这辆小汽车是否超速?
22.小明准备测量学校旗杆的高度,他发现斜坡正对着太阳时,旗杆影子恰好落在水平地面和斜坡坡面上,测得旗杆在水平地面上的影长,在斜坡坡面上的影长,太阳光线与水平地面成角,且太阳光线与斜坡坡面互相垂直,请你帮小明求出旗杆的高度(结果保留根号).
参考答案:
1.D
【分析】本题考查了正切.熟练掌握特殊角的正切是解题的关键.
根据,作答即可.
【详解】解:,
故选:D.
2.A
【分析】本题考查了特殊角的三角函数值,解答本题的关键是掌握几个特殊角的三角函数值.并且根据特殊的三角函数值求解.
【详解】为锐角,,
.
故选:A.
3.D
【分析】本题考查了解直角三角形.由三角函数定义即可得出答案.
【详解】解:由图可得:,
∴.
故选:D.
4.B
【分析】根据余弦的定义计算即可.
【详解】解:如图,
∵中,,,,
∴
在中,,
故选B.
【点睛】本题考查的是锐角三角函数的定义,掌握锐角A的邻边b与斜边c的比叫做角A的余弦是解题的关键.
5.D
【分析】根据特殊角的三角函数值求解即可.
【详解】解:
∴
∴
∴.
故选:D.
【点睛】本题考查的是特殊角的三角函数值,熟记特殊角的三角函数值是解题的关键.
6.B
【分析】根据特殊角的三角函数值分别求出、,根据等边三角形的判定定理判断即可.
【详解】解:∵,
∴,
∴是等边三角形
故选:B.
【点睛】本题考查的是特殊角的三角函数值,等边三角形的判定,熟记、、角的各种三角函数值是解题的关键.
7.C
【分析】利用三角函数值中正切,可得到与的关系,计算即可.
【详解】在中, ,
,
故选C.
【点睛】本题考查三角函数值的应用,注意区分三边对应关系.
8.D
【分析】根据题意以及矩形的性质,勾股定理求得,进而根据得出即可求解.
【详解】解:∵四边形是矩形,,,
∴,,
∵对角线的垂直平分线分别交于点,
∴,,
∵,则,
∴,
∴,
解得:,
故选:D
【点睛】本题考查了矩形的性质,正切的定义,勾股定理,垂直平分线的性质,得出是解题的关键.
9.30
【分析】根据特殊角的三角函数值即可求解.
【详解】解:,
,
故答案为:30.
【点睛】本题考查了由三角函数值求锐角,熟练掌握特殊角的三角函数值是解题的关键.
10.
【分析】坡比,即坡面的垂直高度和水平宽度的比,即坡角的正切值,由此即可求解.
【详解】解:如图所示,,,,
∴设,则,
∴,
故答案为:.
【点睛】本题主要考查坡比的概念及计算方法,掌握其概念和计算方法是解题的关键.
11.
【分析】先画出图形,再根据正弦三角函数的定义即可得.
【详解】解:由题意,画出图形如下:
,
,
故答案为:.
【点睛】本题考查了正弦,熟练掌握正弦的概念是解题关键.
12.
【分析】如图,连接正六边形对角顶点交于O点,将正六边形分成6个全等的等边三角形,过O点作AB边垂线于H点,计算出三角形AOB的面积,乘以6即可求出答案.
【详解】解:如图,连接正六边形对角顶点交于O点,过O点作AB边垂线于H点,
易知为等边三角形,,,
,
这个正六边形底面的面积,
故答案为:.
【点睛】本题考查了正六边形面积计算、利用锐角三角函数解直角三角形等知识点,通过作图将正六边形分成6个全等的等边三角形是解题的突破口.
13.9
【分析】首先根据锐角三角函数得出,再将AB的值代入计算即可.
【详解】在Rt△ABC中,.
∵AB=15,
∴,
解得AC=9.
故答案为:9.
【点睛】本题主要考查了解直角三角形的知识,正确的选择锐角三角函数是解题的关键.
14.9
【分析】根据直角三角形的性质、同角的余角相等得到∠BCD=∠A,根据正切的定义计算即可
【详解】解:∵∠ACB=90°,
∴∠A+∠B=90°,
∵CD⊥AB,
∴∠BCD+∠B=90°,
∴∠BCD=∠A,
在Rt△ACB中,
∵tanA=tan∠BCD==,
∴BC=AC=×12=9.
故答案为:9.
【点睛】本题考查了解直角三角形:掌握正切的定义是解题的关键.
15./0.8
【分析】如图,过点A作AH⊥BC于H.利用勾股定理求出AC即可解决问题.
【详解】解:如图,过点A作AH⊥BC于H.
在Rt△ACH中,∵AH=4,CH=3,
∴AC==5,
∴sin∠ACH=,
故答案为:.
【点睛】本题考查了解直角三角形,解题的关键是学会添加常用辅助线,构造直角三角形解决问题.
16.48
【分析】根据锐角三角函数关系:,即可求解.
【详解】∵是锐角,,
又∵,
∴48°.
故答案是48.
【点睛】本题主要考查锐角三角函数的关系,掌握,是解题的关键.
17.1
【分析】直接利用特殊角的三角函数值代入求出答案即可.
【详解】
,
,
.
【点睛】本题考查实数运算,熟记特殊角的三角函数值是解题的关键.
18.10
【分析】根据∠C=90°,,设BC=5x,AB=13x,再根据勾股定理求出AC =12x,求出x的值,再代入BC=5x,进行计算即可.
【详解】解:在Rt△ABC中,C = 90,
∴
设BC=5x,AB=13x.
由勾股定理得AC =12x.
∵AC =24,
∴12x=24 解得x=2
∴BC=5x=10
【点睛】本题考查了解直角三角形和勾股定理的应用,解此题的关键是得出关于x的方程,难度适中.
19.∠A=60°,,c=40
【分析】直角三角形的两个锐角互余,并且Rt△ABC中,∠C=90°则∠A=90-∠B=60°,解直角三角形就是求直角三角形中除直角以外的两锐角,三边中的未知的元素.
【详解】由∠C=90°知,∠A+∠B=90°,而∠B=30°,
∴∠A=90°-30°=60°,
,
∴,
∴c=40,
由勾股定理知,
∴,
解得:.
【点睛】考查了解直角三角形的条件,已知三角形的一边与一个锐角,就可以求出另一个锐角与三角形的另外两边.
20.63.4m
【分析】过A作AD⊥BC于D,根据∠ABC=60°,∠ACB=45°即可求出BD、CD与AD关系,根据BC=100m,可以求得AD的长度.
【详解】解:过A作AD⊥BC于D,
在Rt△ADB中,∠B=60°,
∴∠BAD=30°,
∴BD=AD tan30°=AD,
在Rt△ADC中,∠C=45°,
∴CD=AD,又BC=100m,
∴BD+CD=AD+AD=100.
解得AD≈63.4m.
答:这段河的宽约为63.4米.
【点睛】本题考查了解直角三角形的应用,解题关键是恰当构建直角三角形,利用三角函数求解.
21.这辆小汽车超速了.
【分析】求出BC的距离,根据时间求出速度,从而可知道是否超速.
【详解】解:根据题意:∠ACB= 90°
由勾股定理可得:
BC=米
40米= 0.04千米,
2秒=小时;
0.04÷= 72千米/时> 70千米/时;
所以超速了.
【点睛】本题考查勾股定理的应用,解题的关键是掌握构造直角三角形,确定直角边,斜边即可.
22.
【分析】延长,交于点,在中,由含30°角的直角三角形的性质求出,得出,再由三角函数求出即可.
【详解】解:延长,交于点,如图所示:
根据平行线的性质得:,
∵在中,,
∴,
则,
在中,
,
答:旗杆的高度为.
【点睛】此题考查了解直角三角形的应用、含30°角的直角三角形的性质,由含30°角的直角三角形的性质求出,得出是解决问题的关键.
