2023-2024学年数学九年级下册人教版第二十六章反比例函数 单元试卷(含解析)
文档属性
| 名称 | 2023-2024学年数学九年级下册人教版第二十六章反比例函数 单元试卷(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 486.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-16 00:00:00 | ||
图片预览


文档简介
2023-2024学年数学九年级下册人教版第二十六章反比例函数
一、单选题
1.反比例函数(其中),当时,y随x的增大而增大,那么m的取值范围是( )
A. B. C. D.
2.在温度不变的条件下,通过不断地对汽缸顶部的活塞加压,测出每一次加压后缸内气体的体积和气体对汽缸壁所产生的压强,数据如下表,可以反映与之间的关系的式子是( )
体积 100 80 60 40 20
压强 60 75 100 150 300
A. B. C. D.
3.若反比例函数()的图象经过点,则k的值是( )
A.2 B. C. D.
4.如图,A是反比例函数的图象上一点,轴于B,点C在x轴上,若面积为2,则k的值为( )
A. B.1 C.2 D.4
5.如果反比例函数的图像在第一、三象限,那么的取值范围是( )
A. B. C. D.
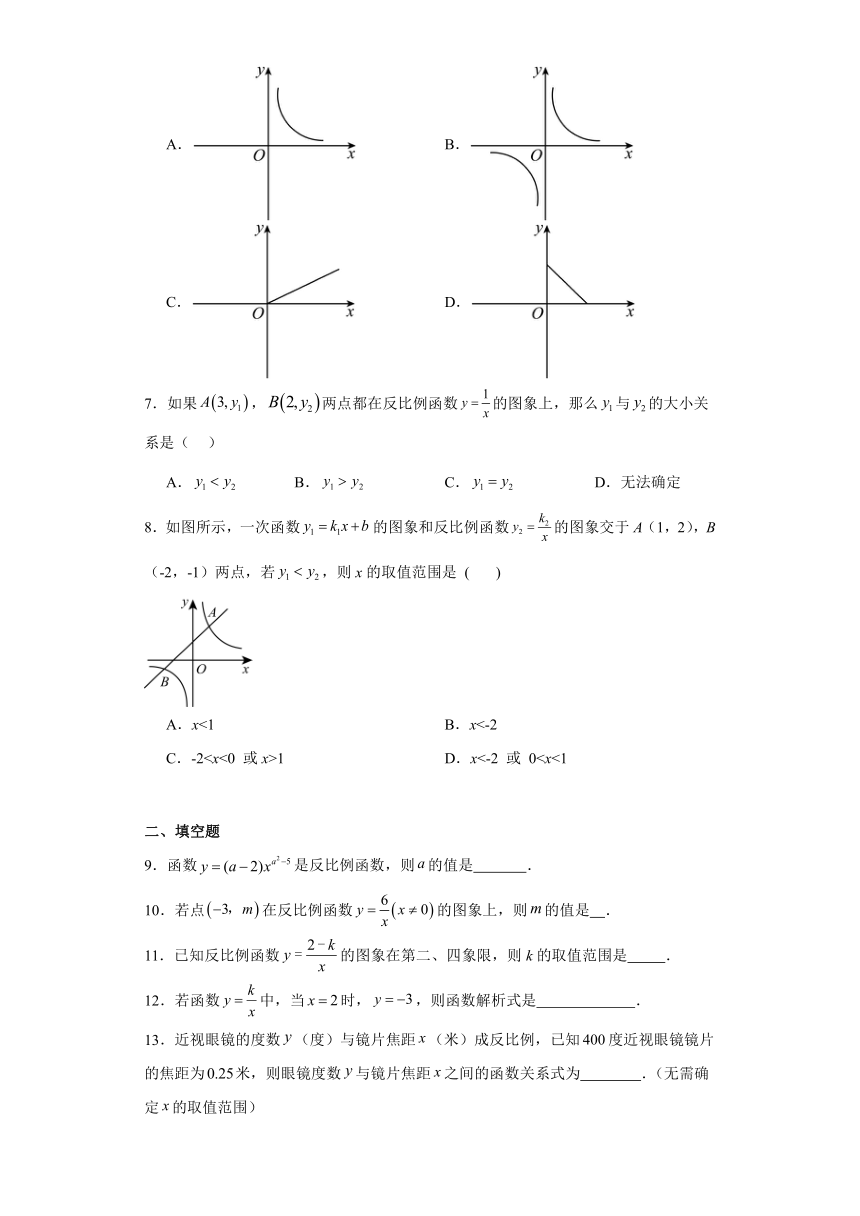
6.已知矩形的面积为 ,它的长y与宽x之间的关系用图象大致可表示为( )
A. B.
C. D.
7.如果,两点都在反比例函数的图象上,那么与的大小关系是( )
A. B. C. D.无法确定
8.如图所示,一次函数的图象和反比例函数的图象交于A(1,2),B(-2,-1)两点,若,则x的取值范围是 ( )
A.x<1 B.x<-2
C.-21 D.x<-2 或 0二、填空题
9.函数是反比例函数,则的值是 .
10.若点在反比例函数的图象上,则的值是 .
11.已知反比例函数的图象在第二、四象限,则k的取值范围是 .
12.若函数中,当时,,则函数解析式是 .
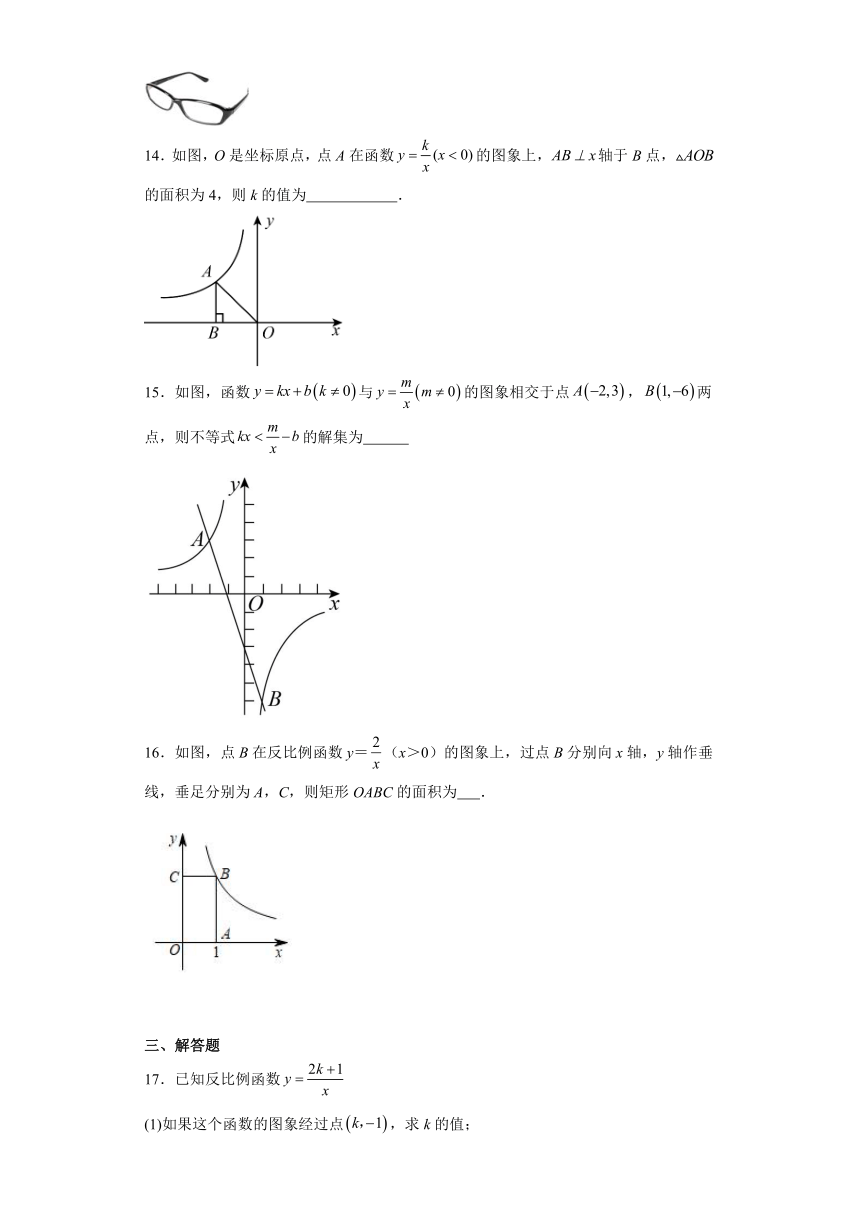
13.近视眼镜的度数(度)与镜片焦距(米)成反比例,已知度近视眼镜镜片的焦距为米,则眼镜度数与镜片焦距之间的函数关系式为 .(无需确定的取值范围)
14.如图,O是坐标原点,点A在函数的图象上,轴于B点,的面积为4,则k的值为 .
15.如图,函数与的图象相交于点,两点,则不等式的解集为
16.如图,点B在反比例函数y=(x>0)的图象上,过点B分别向x轴,y轴作垂线,垂足分别为A,C,则矩形OABC的面积为 .
三、解答题
17.已知反比例函数
(1)如果这个函数的图象经过点,求k的值;
(2)如果在这个函数图象所在的每个象限内,y的值随x的值增大而减小,求k的取值范围.
18.已知反比例函数的图像经过直线上的点,求m和k的值
19.已知反比例函数的图象分别位于第二、第四象限,化简:.
20.小明要把一篇社会调查报告录入电脑,当他以100字/分钟的速度录入文字时,经过240分钟能完成录入.设他录入文字的速度为v字/分钟时,完成录入的时间为t分钟.求t与v之间的函数关系式(不必写出自变量的取值范围).
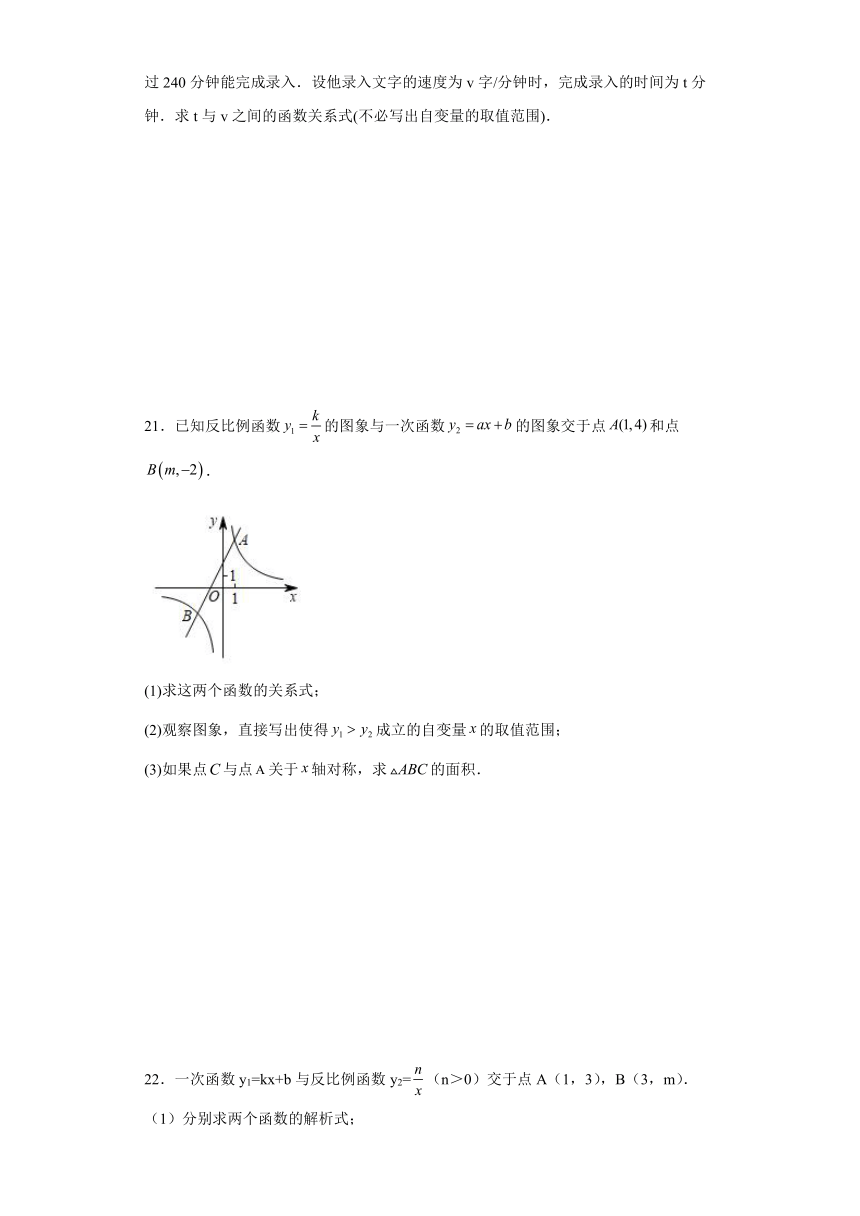
21.已知反比例函数的图象与一次函数的图象交于点和点.
(1)求这两个函数的关系式;
(2)观察图象,直接写出使得成立的自变量的取值范围;
(3)如果点与点关于轴对称,求的面积.
22.一次函数y1=kx+b与反比例函数y2=(n>0)交于点A(1,3),B(3,m).
(1)分别求两个函数的解析式;
(2)根据图像直接写出,当x为何值时,y1<y2;
(3)在x轴上找一点P,使得△OAP的面积为6,求出P点坐标.
参考答案:
1.A
【分析】根据反比例函数的性质得出,进而即可求解.
【详解】解:反比例函数,当时,y随x的增大而增大,
,
,
故选:A.
【点睛】本题考查了反比例函数的性质,解题的关键是掌握反比例函数性质:图像为双曲线,当,图像分布在第一、三象限,在每一象限,y随x的增大而减小;当,图像分布在第二、四象限,在每一象限,y随x的增大而增大.
2.D
【分析】由表格发现,进而可求解.
【详解】解:由表格知,,即,
故选:D.
【点睛】本题考查反比例函数,理解题意,得出因变量与自变量的关系是解答的关键.
3.B
【分析】把点代入反比例函数解析式即可得到答案.
【详解】解:∵反比例函数()的图象经过点,
∴,
解得,
故选:B
【点睛】此题考查了反比例函数,把点的坐标代入函数解析式准确计算是解题的关键.
4.D
【分析】连接,可得,根据反比例函数的几何意义,可求出的值.
【详解】解:连接,
轴,
轴,
,即:,
,或(舍去),
故选:D.
【点睛】本题考查反比例函数的图象和性质,理解反比例函数的几何意义以及同底等高的三角形的面积相等,是解决问题的前提.
5.A
【分析】根据反比例函数的图像与性质:当时,反比例函数图像在第一、三象限,即可解答;
【详解】∵反比例函数的图像在第一、三象限,
∴,
故选:A
【点睛】本题主要考查反比例函数的图像与性质,熟练掌握反比例函数的图像与性质是解题的关键.
6.A
【分析】由长方形的面积公式得,且,,而B中有,的情况,C,D中有或的情况,据此即可得出结果.
【详解】解:,
,,
故选:A.
【点睛】本题考查了反比例函数,解题的关键是理解现实生活中存在大量成反比例函数的两个变量,确定两个变量之间的函数关系,然后利用实际意义确定其所在的象限.
7.A
【分析】根据反比例函数的增减性即可得到答案.
【详解】解:∵反比例函数的图象在每一象限内随的增大而减小,而,两点都在反比例函数第一象限的图象上,
∴
故选:A.
【点睛】本题考查的是反比例函数的性质,掌握“的图象,当时,图象在每一象限内随的增大而减小”是解本题的关键.
8.D
【分析】根据一次函数图象位于反比例函数图象的下方,即可得解.
【详解】根据题意可得,,即一次函数图象位于反比例函数图象的下方,
∴x<-2 或 0故选:D.
【点睛】本题主要考查反比例函数与一次函数的交点问题,难度较易,解此题的关键在于利用函数图形进行判断即可..
9.
【分析】根据题意可知,且,求解即可得到答案.
【详解】根据题意,得
.
解得
,.
又,
所以.
故答案为:.
【点睛】本题主要考查反比例函数的定义以及负整数指数幂的运算,牢记反比例函数的定义以及负整数指数幂的运算法则是解题的关键.
10.
【分析】把代入即可求出答案.
【详解】解:把代入反比例函数得:,
故答案为:.
【点睛】本题主要考查对反比例函数图象上点的坐标特征的理解和掌握,能根据反比例函数图象上点的坐标特征进行计算是解此题的关键.
11.
【分析】根据反比例函数的图象和性质求解,即可得到答案.
【详解】解:反比例函数的图象在第二、四象限,
,
,
故答案为:.
【点睛】本题考查了反比例函数的图象和性质,解题关键是掌握反比例函数中,,函数图象在第一、三象限内;,函数图象在第二、四象限内.
12.
【分析】将,代入函数解析式,求得,即可.
【详解】解:将,代入函数解析式,可得,解得
即函数的解析式为,
故答案为:
【点睛】此题考查了待定系数法求解反比例函数的解析式,解题的关键是掌握待定系数法求解反比例函数解析式.
13./
【分析】根据题意直接列式计算求出值,问题随之得解.
【详解】解:根据题意得,
∴.
故答案为:.
【点睛】本题主要考查了求解反比例函数解析式的知识,明确题意是解答本题的关键.
14.﹣8
【分析】利用反比例函数k的几何意义得到|k|=4,然后根据反比例函数的性质确定k的值.
【详解】解:∵AB⊥x轴,
∴=|k|,即|k|=4,
∵k<0,
∴k=﹣8.
故答案为﹣8.
【点睛】本题主要考查了反比例函数的几何意义,准确计算是解题的关键.
15.或/x>1或-2【分析】把不等式变形为,利用两个函数交点求解即可.
【详解】解:不等式变形为,
根据图象可知,当A点右侧,y轴左侧或在B点右侧时,一次函数值比反比例函数值小,
因为,函数与的图象相交于点,两点,
所以,不等式的解集为或,
故答案为:或.
【点睛】本题考查了一次函数与反比例函数比较大小,解题关键是树立数形结合思想,准确利用图象求解.
16.2
【分析】根据反比例函数k的几何意义求解即可.
【详解】解:∵点B在反比例函数y=(x>0)的图象上,
∴.
∵四边形OABC是矩形,
∴.
∴矩形OABC的面积为=.
故答案为:2.
【点睛】此题考查了反比例函数k的几何意义,解题的关键是熟练掌握反比例函数k的几何意义.反比例函数k的几何意义:反比例函数上任意一点与两坐标轴围成的矩形面积=.
17.(1)
(2)
【分析】(1)将点代入反比例函数解析式即可求出k值;
(2)由这个函数图象所在的每个象限内y的值随x的值增大而减小,可确定,进而可得k的取值范围.
【详解】(1)1)把点(k,—1)代入,得,
∴.
(2)∵在这个函数图象所在的每个象限内,y的值随x的值增大而减小,
∴
解得:.
【点睛】本题主要考查了反比例函数的解析式以及图象和性质,熟练掌握反比例函数的图象和性质是解题的关键.
18.;.
【分析】先将P点坐标代入直线解析式可求出m值,进而可得P点坐标,再将P点坐标代入反比例函数解析式即可得k的值.
【详解】把,代入的左右两边解得;
把,代入的左右两边解得.
【点睛】本题主要考查了正比例函数和反比例函数的解析式,根据解析式求出点的坐标是解题的关键.
19.5
【分析】由反比例函数图象的性质可得k<0,化简分式时注意去绝对值.
【详解】由题意得k<0.
【点睛】本题考查反比例函数图象的性质和分式的化简,关键在于去绝对值时符号的问题.
20.t=.
【分析】根据题意,计算得到社会调查的总字数,根据t与v之间的关系列出关系式即可.
【详解】解:由题意,得vt=240×100,
故t与v之间的关系式为:t=.
【点睛】此题考查了是反比例函数的应用,现实生活中存在大量成反比例函数的两个变量,解答该类问题的关键是确定两个变量之间的函数关系,然后利用待定系数法求出它们的关系式.
21.(1),
(2)或
(3)12
【分析】(1)把代入反比例函数解析式即可求出k值,根据反比例函数解析式求出点B的坐标,再利用待定系数法求一次函数的解析式;
(2)当反比例函数图像在一次函数图象上方时,,结合两个交点的横坐标即可求解;
(3)求出点C的坐标,利用三角形面积公式即可求解.
【详解】(1)解:将代入得,,
解得,
反比例函数的解析式为,
又点在上,
,
解得,
点B的坐标为,
点A和点B在一次函数上,
,
解得,
一次函数的解析式为,
综上可得,.
(2)解:时,反比例函数图象在一次函数图象上方,
观察图象可知,当或时,.
(3)解:如图,作点关于轴的对称点,连接AC,作于点D,
点A的坐标为,
点C的坐标为,
又点B的坐标为,
,,
的面积.
【点睛】本题考查利用待定系数法求一次函数、反比例函数的解析式,以及求三角形的面积,其中第2问用到了数形结合的思想,第3问用到了求坐标系内两点之间的距离,都是常考题型,需要多加练习.
22.(1)y2=,y1=-x+4.(2)x<1或x>3.(3)(-4,0)或(4,0).
【分析】(1)首先将A,B两点坐标代入反比例函数解析式,得出m,n的值,在利用待定系数法即可解决问题;
(2)观察图象,写出一次函数的图象在反比例函数图象下方时,x的取值范围即可;
(3)由题意可知A的纵坐标的值即为△OAP的高,且P点在横轴上,根据三角形的面积公式可知OP的长为4,写出可能的坐标即可.
【详解】解:(1)将A(1,3),代入y2=(n>0),得n=3,
再将B(3,m)代入y2=,得m=1,
所以将A,B两点坐标代入y1=kx+b,
得,
解得,
∴一次函数解析式为y1=-x+4;
(2)根据题意的一次函数的图象在反比例函数图象下方时所对应的x的取值范围即为所求,此时x的范围是:x<1或x>3;
(3)由题意得△OAP的高为3
∴S△OAP=·3·|OP|=6,
∴OP的长为4,
又∵点P在x轴上,
∴点P的坐标为(-4,0)或(4,0).
【点睛】本题考查了一次函数和反比例函数的交点问题,根据题意细心分析是解题关键.
一、单选题
1.反比例函数(其中),当时,y随x的增大而增大,那么m的取值范围是( )
A. B. C. D.
2.在温度不变的条件下,通过不断地对汽缸顶部的活塞加压,测出每一次加压后缸内气体的体积和气体对汽缸壁所产生的压强,数据如下表,可以反映与之间的关系的式子是( )
体积 100 80 60 40 20
压强 60 75 100 150 300
A. B. C. D.
3.若反比例函数()的图象经过点,则k的值是( )
A.2 B. C. D.
4.如图,A是反比例函数的图象上一点,轴于B,点C在x轴上,若面积为2,则k的值为( )
A. B.1 C.2 D.4
5.如果反比例函数的图像在第一、三象限,那么的取值范围是( )
A. B. C. D.
6.已知矩形的面积为 ,它的长y与宽x之间的关系用图象大致可表示为( )
A. B.
C. D.
7.如果,两点都在反比例函数的图象上,那么与的大小关系是( )
A. B. C. D.无法确定
8.如图所示,一次函数的图象和反比例函数的图象交于A(1,2),B(-2,-1)两点,若,则x的取值范围是 ( )
A.x<1 B.x<-2
C.-2
9.函数是反比例函数,则的值是 .
10.若点在反比例函数的图象上,则的值是 .
11.已知反比例函数的图象在第二、四象限,则k的取值范围是 .
12.若函数中,当时,,则函数解析式是 .
13.近视眼镜的度数(度)与镜片焦距(米)成反比例,已知度近视眼镜镜片的焦距为米,则眼镜度数与镜片焦距之间的函数关系式为 .(无需确定的取值范围)
14.如图,O是坐标原点,点A在函数的图象上,轴于B点,的面积为4,则k的值为 .
15.如图,函数与的图象相交于点,两点,则不等式的解集为
16.如图,点B在反比例函数y=(x>0)的图象上,过点B分别向x轴,y轴作垂线,垂足分别为A,C,则矩形OABC的面积为 .
三、解答题
17.已知反比例函数
(1)如果这个函数的图象经过点,求k的值;
(2)如果在这个函数图象所在的每个象限内,y的值随x的值增大而减小,求k的取值范围.
18.已知反比例函数的图像经过直线上的点,求m和k的值
19.已知反比例函数的图象分别位于第二、第四象限,化简:.
20.小明要把一篇社会调查报告录入电脑,当他以100字/分钟的速度录入文字时,经过240分钟能完成录入.设他录入文字的速度为v字/分钟时,完成录入的时间为t分钟.求t与v之间的函数关系式(不必写出自变量的取值范围).
21.已知反比例函数的图象与一次函数的图象交于点和点.
(1)求这两个函数的关系式;
(2)观察图象,直接写出使得成立的自变量的取值范围;
(3)如果点与点关于轴对称,求的面积.
22.一次函数y1=kx+b与反比例函数y2=(n>0)交于点A(1,3),B(3,m).
(1)分别求两个函数的解析式;
(2)根据图像直接写出,当x为何值时,y1<y2;
(3)在x轴上找一点P,使得△OAP的面积为6,求出P点坐标.
参考答案:
1.A
【分析】根据反比例函数的性质得出,进而即可求解.
【详解】解:反比例函数,当时,y随x的增大而增大,
,
,
故选:A.
【点睛】本题考查了反比例函数的性质,解题的关键是掌握反比例函数性质:图像为双曲线,当,图像分布在第一、三象限,在每一象限,y随x的增大而减小;当,图像分布在第二、四象限,在每一象限,y随x的增大而增大.
2.D
【分析】由表格发现,进而可求解.
【详解】解:由表格知,,即,
故选:D.
【点睛】本题考查反比例函数,理解题意,得出因变量与自变量的关系是解答的关键.
3.B
【分析】把点代入反比例函数解析式即可得到答案.
【详解】解:∵反比例函数()的图象经过点,
∴,
解得,
故选:B
【点睛】此题考查了反比例函数,把点的坐标代入函数解析式准确计算是解题的关键.
4.D
【分析】连接,可得,根据反比例函数的几何意义,可求出的值.
【详解】解:连接,
轴,
轴,
,即:,
,或(舍去),
故选:D.
【点睛】本题考查反比例函数的图象和性质,理解反比例函数的几何意义以及同底等高的三角形的面积相等,是解决问题的前提.
5.A
【分析】根据反比例函数的图像与性质:当时,反比例函数图像在第一、三象限,即可解答;
【详解】∵反比例函数的图像在第一、三象限,
∴,
故选:A
【点睛】本题主要考查反比例函数的图像与性质,熟练掌握反比例函数的图像与性质是解题的关键.
6.A
【分析】由长方形的面积公式得,且,,而B中有,的情况,C,D中有或的情况,据此即可得出结果.
【详解】解:,
,,
故选:A.
【点睛】本题考查了反比例函数,解题的关键是理解现实生活中存在大量成反比例函数的两个变量,确定两个变量之间的函数关系,然后利用实际意义确定其所在的象限.
7.A
【分析】根据反比例函数的增减性即可得到答案.
【详解】解:∵反比例函数的图象在每一象限内随的增大而减小,而,两点都在反比例函数第一象限的图象上,
∴
故选:A.
【点睛】本题考查的是反比例函数的性质,掌握“的图象,当时,图象在每一象限内随的增大而减小”是解本题的关键.
8.D
【分析】根据一次函数图象位于反比例函数图象的下方,即可得解.
【详解】根据题意可得,,即一次函数图象位于反比例函数图象的下方,
∴x<-2 或 0
【点睛】本题主要考查反比例函数与一次函数的交点问题,难度较易,解此题的关键在于利用函数图形进行判断即可..
9.
【分析】根据题意可知,且,求解即可得到答案.
【详解】根据题意,得
.
解得
,.
又,
所以.
故答案为:.
【点睛】本题主要考查反比例函数的定义以及负整数指数幂的运算,牢记反比例函数的定义以及负整数指数幂的运算法则是解题的关键.
10.
【分析】把代入即可求出答案.
【详解】解:把代入反比例函数得:,
故答案为:.
【点睛】本题主要考查对反比例函数图象上点的坐标特征的理解和掌握,能根据反比例函数图象上点的坐标特征进行计算是解此题的关键.
11.
【分析】根据反比例函数的图象和性质求解,即可得到答案.
【详解】解:反比例函数的图象在第二、四象限,
,
,
故答案为:.
【点睛】本题考查了反比例函数的图象和性质,解题关键是掌握反比例函数中,,函数图象在第一、三象限内;,函数图象在第二、四象限内.
12.
【分析】将,代入函数解析式,求得,即可.
【详解】解:将,代入函数解析式,可得,解得
即函数的解析式为,
故答案为:
【点睛】此题考查了待定系数法求解反比例函数的解析式,解题的关键是掌握待定系数法求解反比例函数解析式.
13./
【分析】根据题意直接列式计算求出值,问题随之得解.
【详解】解:根据题意得,
∴.
故答案为:.
【点睛】本题主要考查了求解反比例函数解析式的知识,明确题意是解答本题的关键.
14.﹣8
【分析】利用反比例函数k的几何意义得到|k|=4,然后根据反比例函数的性质确定k的值.
【详解】解:∵AB⊥x轴,
∴=|k|,即|k|=4,
∵k<0,
∴k=﹣8.
故答案为﹣8.
【点睛】本题主要考查了反比例函数的几何意义,准确计算是解题的关键.
15.或/x>1或-2
【详解】解:不等式变形为,
根据图象可知,当A点右侧,y轴左侧或在B点右侧时,一次函数值比反比例函数值小,
因为,函数与的图象相交于点,两点,
所以,不等式的解集为或,
故答案为:或.
【点睛】本题考查了一次函数与反比例函数比较大小,解题关键是树立数形结合思想,准确利用图象求解.
16.2
【分析】根据反比例函数k的几何意义求解即可.
【详解】解:∵点B在反比例函数y=(x>0)的图象上,
∴.
∵四边形OABC是矩形,
∴.
∴矩形OABC的面积为=.
故答案为:2.
【点睛】此题考查了反比例函数k的几何意义,解题的关键是熟练掌握反比例函数k的几何意义.反比例函数k的几何意义:反比例函数上任意一点与两坐标轴围成的矩形面积=.
17.(1)
(2)
【分析】(1)将点代入反比例函数解析式即可求出k值;
(2)由这个函数图象所在的每个象限内y的值随x的值增大而减小,可确定,进而可得k的取值范围.
【详解】(1)1)把点(k,—1)代入,得,
∴.
(2)∵在这个函数图象所在的每个象限内,y的值随x的值增大而减小,
∴
解得:.
【点睛】本题主要考查了反比例函数的解析式以及图象和性质,熟练掌握反比例函数的图象和性质是解题的关键.
18.;.
【分析】先将P点坐标代入直线解析式可求出m值,进而可得P点坐标,再将P点坐标代入反比例函数解析式即可得k的值.
【详解】把,代入的左右两边解得;
把,代入的左右两边解得.
【点睛】本题主要考查了正比例函数和反比例函数的解析式,根据解析式求出点的坐标是解题的关键.
19.5
【分析】由反比例函数图象的性质可得k<0,化简分式时注意去绝对值.
【详解】由题意得k<0.
【点睛】本题考查反比例函数图象的性质和分式的化简,关键在于去绝对值时符号的问题.
20.t=.
【分析】根据题意,计算得到社会调查的总字数,根据t与v之间的关系列出关系式即可.
【详解】解:由题意,得vt=240×100,
故t与v之间的关系式为:t=.
【点睛】此题考查了是反比例函数的应用,现实生活中存在大量成反比例函数的两个变量,解答该类问题的关键是确定两个变量之间的函数关系,然后利用待定系数法求出它们的关系式.
21.(1),
(2)或
(3)12
【分析】(1)把代入反比例函数解析式即可求出k值,根据反比例函数解析式求出点B的坐标,再利用待定系数法求一次函数的解析式;
(2)当反比例函数图像在一次函数图象上方时,,结合两个交点的横坐标即可求解;
(3)求出点C的坐标,利用三角形面积公式即可求解.
【详解】(1)解:将代入得,,
解得,
反比例函数的解析式为,
又点在上,
,
解得,
点B的坐标为,
点A和点B在一次函数上,
,
解得,
一次函数的解析式为,
综上可得,.
(2)解:时,反比例函数图象在一次函数图象上方,
观察图象可知,当或时,.
(3)解:如图,作点关于轴的对称点,连接AC,作于点D,
点A的坐标为,
点C的坐标为,
又点B的坐标为,
,,
的面积.
【点睛】本题考查利用待定系数法求一次函数、反比例函数的解析式,以及求三角形的面积,其中第2问用到了数形结合的思想,第3问用到了求坐标系内两点之间的距离,都是常考题型,需要多加练习.
22.(1)y2=,y1=-x+4.(2)x<1或x>3.(3)(-4,0)或(4,0).
【分析】(1)首先将A,B两点坐标代入反比例函数解析式,得出m,n的值,在利用待定系数法即可解决问题;
(2)观察图象,写出一次函数的图象在反比例函数图象下方时,x的取值范围即可;
(3)由题意可知A的纵坐标的值即为△OAP的高,且P点在横轴上,根据三角形的面积公式可知OP的长为4,写出可能的坐标即可.
【详解】解:(1)将A(1,3),代入y2=(n>0),得n=3,
再将B(3,m)代入y2=,得m=1,
所以将A,B两点坐标代入y1=kx+b,
得,
解得,
∴一次函数解析式为y1=-x+4;
(2)根据题意的一次函数的图象在反比例函数图象下方时所对应的x的取值范围即为所求,此时x的范围是:x<1或x>3;
(3)由题意得△OAP的高为3
∴S△OAP=·3·|OP|=6,
∴OP的长为4,
又∵点P在x轴上,
∴点P的坐标为(-4,0)或(4,0).
【点睛】本题考查了一次函数和反比例函数的交点问题,根据题意细心分析是解题关键.
