北师大版数学八年级下册6.2 平行四边形的判定 第2课时 课件 (共17张PPT)
文档属性
| 名称 | 北师大版数学八年级下册6.2 平行四边形的判定 第2课时 课件 (共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 178.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-16 00:00:00 | ||
图片预览





文档简介
(共17张PPT)
第六章 平行四边形
6.2 平行四边形的判定
第2课时
学习导航
学习目标
新课导入
合作探究
当堂检测
课堂总结
一、学习目标
1.经历平行四边形判定方法3的探究过程,学会运用“对角线互相
平分的四边形是平行四边形”进行判定
2.能综合运用平行四边形的四种判定方法进行证明
二、新课导入
回顾与思考:
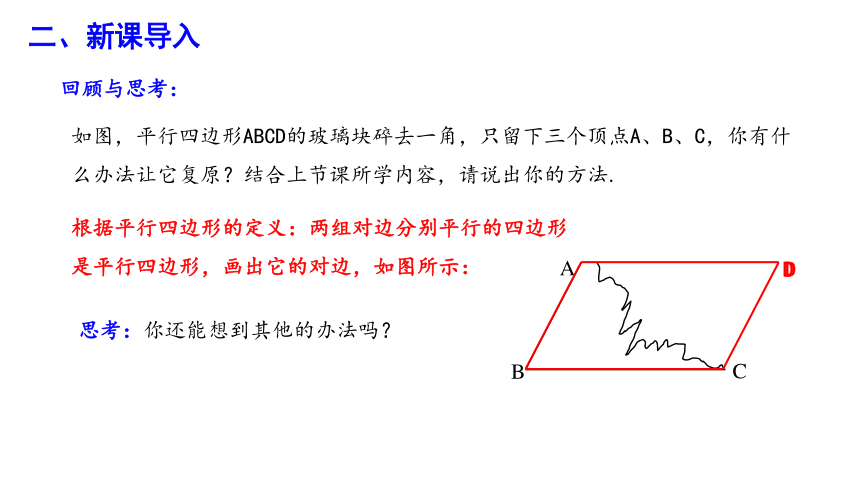
如图,平行四边形ABCD的玻璃块碎去一角,只留下三个顶点A、B、C,你有什么办法让它复原?结合上节课所学内容,请说出你的方法.
根据平行四边形的定义:两组对边分别平行的四边形
是平行四边形,画出它的对边,如图所示:
思考:你还能想到其他的办法吗?
A
B
C
D
D
三、合作探究
探究一 平行四边形的判定方法
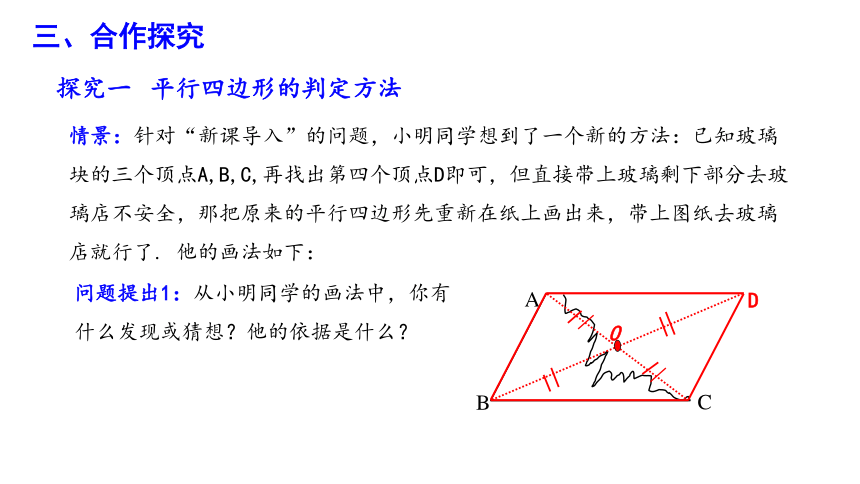
情景:针对“新课导入”的问题,小明同学想到了一个新的方法:已知玻璃块的三个顶点A,B,C,再找出第四个顶点D即可,但直接带上玻璃剩下部分去玻璃店不安全,那把原来的平行四边形先重新在纸上画出来,带上图纸去玻璃店就行了. 他的画法如下:
A
B
C
D
O
问题提出1:从小明同学的画法中,你有什么发现或猜想?他的依据是什么?
问题探究:
已知平行四边形三个顶点A,B,C,小明的画法是根据平行四边形 的 性质,画出了平行四边形的另外一个点D.
对角线互相平分
猜想:
对角线互相平分的四边形是平行四边形.
探究一 平行四边形的判定方法
这个猜想是否
正确呢?
三、合作探究
问题提出2:已知:如图,四边形ABCD的两条对角线AC与BD相交于点O, 并且 OA=OC,OB=OD. 求证:四边形ABCD是平行四边形.
问题探究:
已知OA=OC,OB=OD,∠ =∠ ,易证△AOD≌△COB,从而可以说明四边形ABCD的对边AB=CD、 ,即可证明四边形ABCD是平行四边形,这是根据平行四边形的判定定理:
.
AOD
COB
AD=BC
两组对边分别相等的四边形是平行四边形
探究一 平行四边形的判定方法
三、合作探究
问题解决:
∵OA=OC,OB=OD,∠AOB=∠COD,
∴△AOB≌△COD,
∴AB=CD,同理,AD=BC,
∴四边形ABCD是平行四边形.
(两组对边分别相等的四边形是平行四边形)
结论:
对角线互相平分的四边形是平行四边形.
平行四边形的判定方法3:
讨论:你还有别的方法吗?
三、合作探究
练一练:
证明:∵OA=OC,OD=OB,∠AOD=∠COB.
∴△AOD≌△COB.
∴AD=CB,∠ADO=∠CBO.
∴AD∥CB.
∴四边形ABCD是平行四边形.
(一组对边平行且相等的四边形是平行四边形)
1.已知:如图,四边形ABCD的两条对角线AC与BD相交于点O, 并且OA=OC,OB=OD. 求证:四边形ABCD是平行四边形.
三、合作探究
探究二 平行四边形的判定方法的综合应用
问题提出:已知:如图,E,F是平行四边形ABCD对角线AC上的两点,且AE=CF. 求证:四边形BFDE是平行四边形.
问题探究:
结合题意,我们已知平行四边形ABCD的一条对角线,
可画出另一条对角线 ,如图,这条对角线也在
四边形BFDE中,只需再说明对角线 = ,即可
求证BFDE是平行四边形,这是利用了平行四边形的
判定方法: .
对角线互相平分的四边形是平行四边形
BD
O
OE
OF
三、合作探究
问题解决:
证明:如图,连接BD,交AC于点O.
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD(平行四边形的对角线互相平分).
∵AE=CF,
∴OA-AE=OC-CF,即OE=OF.
∴四边形BFDE是平行四边形
(对角线互相平分的四边形是平行四边形).
探究二 平行四边形的判定方法的综合应用
O
三、合作探究
练一练:
2.如图,在平行四边形ABCDA中,对角线AC与BD相交于点O,点E,F分别是
OA和OC的中点,四边形BFDE是平行四边形吗?请说明理由.
四边形BFDE是平行四边形,
理由:∵四边形ABCD是平行四边形,
∴OB=OD,OA=OC.
又∵E,F分别是OA和OC的中点,
∴OE=OF.
∴四边形BFDE是平行四边形.
三、合作探究
四、当堂检测
1.下列说法错误的是( )
A.对角线互相平分的四边形是平行四边形
B.两组对边分别相等的四边形是平行四边形
C.一组对边平行且相等的四边形是平行四边形
D.一组对边相等,另一组对边平行的四边形是平行四边形
D
2.如图,AD=BC,要使四边形ABCD是平行四边形,还需补充的一个条件是
(横线只需填一个你认为合适的条件即可).
①AD∥BC
②AB=CD
③∠A+∠B=180°
④∠C+∠D=180°等
答案不唯一
四、当堂检测
3.如图,在△ABC中,D是BC边的中点,F,E分别是AD及其延长线上的点,CF∥BE.
(1)△BDE与△CDF全等吗 请说明理由.
解: (1)△BDE≌△CDF.
理由: ∵CF∥BE,
∵D是BC的中点,
又∵∠FDC=∠EDB,
∴△CDF≌△BDE(ASA).
∴∠FCD=∠EBD,
∴CD=BD,
四、当堂检测
3.如图,在△ABC中,D是BC边的中点,F,E分别是AD及其延长线上的点,CF∥BE.
(2)连接BF、CE,试判断四边形BECF是何种特殊四边形,并说明理由.
(2)四边形BECF是平行四边形.
理由: ∵△CDF≌△BDE,
∴DF=DE,
又∵CD=BD,
∴四边形BECF是平行四边形.
四、当堂检测
五、课堂总结
1.两组对边分别平行的四边形是平行四边形.
平行四边形的判定方法:
2.两组对边分别相等的四边形是平行四边形.
3.一组对边平行且相等的四边形是平行四边形.
4.对角线互相平分的四边形是平行四边形.
第六章 平行四边形
6.2 平行四边形的判定
第2课时
学习导航
学习目标
新课导入
合作探究
当堂检测
课堂总结
一、学习目标
1.经历平行四边形判定方法3的探究过程,学会运用“对角线互相
平分的四边形是平行四边形”进行判定
2.能综合运用平行四边形的四种判定方法进行证明
二、新课导入
回顾与思考:
如图,平行四边形ABCD的玻璃块碎去一角,只留下三个顶点A、B、C,你有什么办法让它复原?结合上节课所学内容,请说出你的方法.
根据平行四边形的定义:两组对边分别平行的四边形
是平行四边形,画出它的对边,如图所示:
思考:你还能想到其他的办法吗?
A
B
C
D
D
三、合作探究
探究一 平行四边形的判定方法
情景:针对“新课导入”的问题,小明同学想到了一个新的方法:已知玻璃块的三个顶点A,B,C,再找出第四个顶点D即可,但直接带上玻璃剩下部分去玻璃店不安全,那把原来的平行四边形先重新在纸上画出来,带上图纸去玻璃店就行了. 他的画法如下:
A
B
C
D
O
问题提出1:从小明同学的画法中,你有什么发现或猜想?他的依据是什么?
问题探究:
已知平行四边形三个顶点A,B,C,小明的画法是根据平行四边形 的 性质,画出了平行四边形的另外一个点D.
对角线互相平分
猜想:
对角线互相平分的四边形是平行四边形.
探究一 平行四边形的判定方法
这个猜想是否
正确呢?
三、合作探究
问题提出2:已知:如图,四边形ABCD的两条对角线AC与BD相交于点O, 并且 OA=OC,OB=OD. 求证:四边形ABCD是平行四边形.
问题探究:
已知OA=OC,OB=OD,∠ =∠ ,易证△AOD≌△COB,从而可以说明四边形ABCD的对边AB=CD、 ,即可证明四边形ABCD是平行四边形,这是根据平行四边形的判定定理:
.
AOD
COB
AD=BC
两组对边分别相等的四边形是平行四边形
探究一 平行四边形的判定方法
三、合作探究
问题解决:
∵OA=OC,OB=OD,∠AOB=∠COD,
∴△AOB≌△COD,
∴AB=CD,同理,AD=BC,
∴四边形ABCD是平行四边形.
(两组对边分别相等的四边形是平行四边形)
结论:
对角线互相平分的四边形是平行四边形.
平行四边形的判定方法3:
讨论:你还有别的方法吗?
三、合作探究
练一练:
证明:∵OA=OC,OD=OB,∠AOD=∠COB.
∴△AOD≌△COB.
∴AD=CB,∠ADO=∠CBO.
∴AD∥CB.
∴四边形ABCD是平行四边形.
(一组对边平行且相等的四边形是平行四边形)
1.已知:如图,四边形ABCD的两条对角线AC与BD相交于点O, 并且OA=OC,OB=OD. 求证:四边形ABCD是平行四边形.
三、合作探究
探究二 平行四边形的判定方法的综合应用
问题提出:已知:如图,E,F是平行四边形ABCD对角线AC上的两点,且AE=CF. 求证:四边形BFDE是平行四边形.
问题探究:
结合题意,我们已知平行四边形ABCD的一条对角线,
可画出另一条对角线 ,如图,这条对角线也在
四边形BFDE中,只需再说明对角线 = ,即可
求证BFDE是平行四边形,这是利用了平行四边形的
判定方法: .
对角线互相平分的四边形是平行四边形
BD
O
OE
OF
三、合作探究
问题解决:
证明:如图,连接BD,交AC于点O.
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD(平行四边形的对角线互相平分).
∵AE=CF,
∴OA-AE=OC-CF,即OE=OF.
∴四边形BFDE是平行四边形
(对角线互相平分的四边形是平行四边形).
探究二 平行四边形的判定方法的综合应用
O
三、合作探究
练一练:
2.如图,在平行四边形ABCDA中,对角线AC与BD相交于点O,点E,F分别是
OA和OC的中点,四边形BFDE是平行四边形吗?请说明理由.
四边形BFDE是平行四边形,
理由:∵四边形ABCD是平行四边形,
∴OB=OD,OA=OC.
又∵E,F分别是OA和OC的中点,
∴OE=OF.
∴四边形BFDE是平行四边形.
三、合作探究
四、当堂检测
1.下列说法错误的是( )
A.对角线互相平分的四边形是平行四边形
B.两组对边分别相等的四边形是平行四边形
C.一组对边平行且相等的四边形是平行四边形
D.一组对边相等,另一组对边平行的四边形是平行四边形
D
2.如图,AD=BC,要使四边形ABCD是平行四边形,还需补充的一个条件是
(横线只需填一个你认为合适的条件即可).
①AD∥BC
②AB=CD
③∠A+∠B=180°
④∠C+∠D=180°等
答案不唯一
四、当堂检测
3.如图,在△ABC中,D是BC边的中点,F,E分别是AD及其延长线上的点,CF∥BE.
(1)△BDE与△CDF全等吗 请说明理由.
解: (1)△BDE≌△CDF.
理由: ∵CF∥BE,
∵D是BC的中点,
又∵∠FDC=∠EDB,
∴△CDF≌△BDE(ASA).
∴∠FCD=∠EBD,
∴CD=BD,
四、当堂检测
3.如图,在△ABC中,D是BC边的中点,F,E分别是AD及其延长线上的点,CF∥BE.
(2)连接BF、CE,试判断四边形BECF是何种特殊四边形,并说明理由.
(2)四边形BECF是平行四边形.
理由: ∵△CDF≌△BDE,
∴DF=DE,
又∵CD=BD,
∴四边形BECF是平行四边形.
四、当堂检测
五、课堂总结
1.两组对边分别平行的四边形是平行四边形.
平行四边形的判定方法:
2.两组对边分别相等的四边形是平行四边形.
3.一组对边平行且相等的四边形是平行四边形.
4.对角线互相平分的四边形是平行四边形.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
