6.2.1实数 课件(共22张PPT) 沪科版七年级数学下册
文档属性
| 名称 | 6.2.1实数 课件(共22张PPT) 沪科版七年级数学下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 307.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-16 00:00:00 | ||
图片预览








文档简介
(共22张PPT)
第6章 实数
6.2 实数 第1课时
学习导航
学习目标
新课导入
自主学习
合作探究
当堂检测
课堂总结
一、学习目标
1.了解无理数发现的历程,知道无理数是客观存在的;
2.知道实数的概念并能对实数进行正确的分类,会判断一个数是
有理数还是无理数;(重点)
3.会将循环小数化为分数.
二、新课导入
属于哪一类数呢?
第一次数学危机
公元前500年,古希腊毕达哥拉斯学派的弟子希勃索斯发现了一个惊人的事实,
一个正方形的对角线与其一边的长度是不可公度的(若正方形边长是1,则对角
线的长不是一个有理数)这一不可公度性与毕氏学派“万物皆为数”(指有理数)
的哲理大相径庭.这一发现使该学派领导人惶恐、恼怒,认为这将动摇他们在
学术界的统治地位.
三、自主学习
问题1 我们知道有理数包括整数和分数,利用计算器把下列分数写成小数的形式,它们有什么特征?
它们都可以化成有限小数或无限循环小数的形式
知识点一 无理数的概念
.
. .
三、自主学习
问题2 整数能写成小数的形式吗?3可以看成是3.0吗?
可以
思考 由此你可以得到什么结论?
有理数都可以化成有限小数或无限循环小数的形式.
反过来,任何有限小数或无限循环小数的也都是有理数.
三、自主学习
想一想:所有的数都可以写成有限小数和无限循环小数的形式吗?
π=3.1415926535897932384626…
1.01001000100001…
(两个1之间依次多一个0)
无限不循环小数叫做无理数.
=1.4142135623709504880168…
有些数不可以写成有限小数和无限循环小数的形式,如:
它们是无限不循环小数.
三、自主学习
我们常见的无理数有以下三种形式:
(1)含 的一些数;
(2)含开不尽方的数;
(3)无限不循环的小数,如1.01001000100001…
要点归纳:
三、自主学习
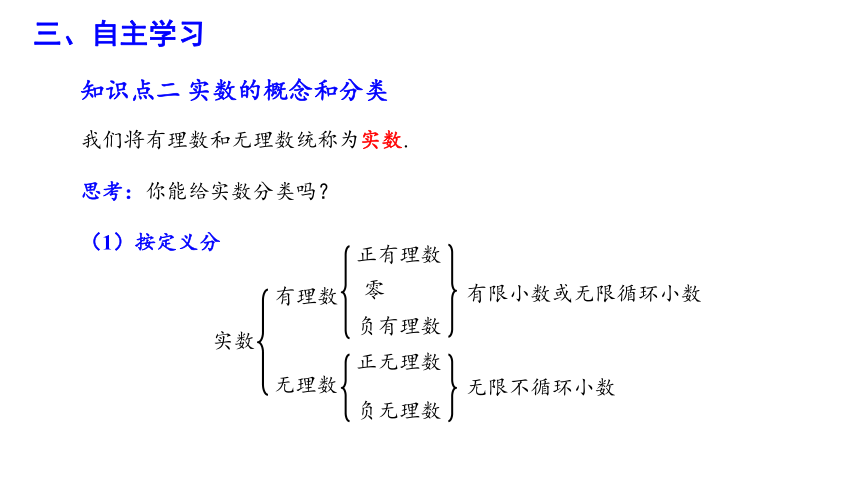
思考:你能给实数分类吗?
(1)按定义分
有理数
无理数
实数
正无理数
负无理数
正有理数
负有理数
零
有限小数或无限循环小数
无限不循环小数
知识点二 实数的概念和分类
我们将有理数和无理数统称为实数.
三、自主学习
(2)按性质分
正实数
负实数
0
实数
分类时要注意什么
不重不漏原则
四、合作探究
探究一 区分有理数和无理数
活动把下列各数分别填入相应的括号内:
0.101,
有理数
无理数
...
...
四、合作探究
练一练
1.判断下列数哪些是有理数?哪些是无理数?
有理数是:
1.23,
..
无理数是:
1.232232223...(两个3之间依次多一个2).
四、合作探究
探究二 实数的分类
活动:把下列各数填入相应的集合内.
(1)有理数集合:{ …};
(2)无理数集合:{ …};
(3)正实数集合:{ …};
(4)负实数集合:{ …}.
四、合作探究
练一练
3,
-3,
0,
π,
3,
探究二 循环小数化为分数
四、合作探究
问题提出:我们知道任何循环小数都能化为分数,那么循环小数如何
化为分数呢?
我们把循环小数分为纯循环小数例如 ,和混循环小数例如 .
问题探究1:纯循环小数化成分数
.
..
.
...
——.
( )
( )
( )
( )
5
21
999
212
根据提示完成下列的填空,并用计算器检验.
四、合作探究
.
..
.
...
观察转化结果,根据你的猜想完成下面结论.
结论1:纯循环小数转化为分数:
每个循环节有几位数字,分数的分母中就有几个 ;
分子则是 .
9
一个循环节的数
四、合作探究
问题探究2:混循环小数化成分数
用计算器检验下列转化是否正确.
.
..
...
观察转化步骤,根据你的猜想完成下面结论.
结论2:混循环小数转化为分数:
每个循环节都有几位数字,分数的分母中就有几个 ,不循环的部分有几位数字,分母中9的后面就有几个 ;
分子则是第一个循环节及它前面的数减去 .
9
0
不循环部分
四、合作探究
练一练
3.将下列循环小数化为分数.
.
.
..
. .
解:
.
.
..
. .
五、当堂检测
1.判断题:
①实数不是有理数就是无理数.( )
③无理数都是无限小数.( )
④带根号的数都是无理数.( )
⑤无理数一定都带根号.( )
⑥两个无理数之积不一定是无理数.( )
⑦两个无理数之和一定是无理数.( )
⑧数轴上的任何一点都可以表示实数.( )
×
×
×
②无理数都是无限不循环小数.( )
√
√
√
√
√
五、当堂检测
2.下列各数中,哪些是有理数?哪些是无理数?
(相邻两个1之间0的个数逐次加1).
解: 是有理数;
π+2, 0.10100100001...是无理数.
五、当堂检测
3.把下列各数分别填入相应的括号内:
(相邻两个3之间的7的个数逐次加1)
有理数
无理数
0,
0.3737737773...,
π,
六、课堂总结
无理数
带省略号且不循环的小数
有特殊意义的数,如π等
带根号,但被开方数是开方不尽的数
概念
实数
有理数
无限不循环小数
第6章 实数
6.2 实数 第1课时
学习导航
学习目标
新课导入
自主学习
合作探究
当堂检测
课堂总结
一、学习目标
1.了解无理数发现的历程,知道无理数是客观存在的;
2.知道实数的概念并能对实数进行正确的分类,会判断一个数是
有理数还是无理数;(重点)
3.会将循环小数化为分数.
二、新课导入
属于哪一类数呢?
第一次数学危机
公元前500年,古希腊毕达哥拉斯学派的弟子希勃索斯发现了一个惊人的事实,
一个正方形的对角线与其一边的长度是不可公度的(若正方形边长是1,则对角
线的长不是一个有理数)这一不可公度性与毕氏学派“万物皆为数”(指有理数)
的哲理大相径庭.这一发现使该学派领导人惶恐、恼怒,认为这将动摇他们在
学术界的统治地位.
三、自主学习
问题1 我们知道有理数包括整数和分数,利用计算器把下列分数写成小数的形式,它们有什么特征?
它们都可以化成有限小数或无限循环小数的形式
知识点一 无理数的概念
.
. .
三、自主学习
问题2 整数能写成小数的形式吗?3可以看成是3.0吗?
可以
思考 由此你可以得到什么结论?
有理数都可以化成有限小数或无限循环小数的形式.
反过来,任何有限小数或无限循环小数的也都是有理数.
三、自主学习
想一想:所有的数都可以写成有限小数和无限循环小数的形式吗?
π=3.1415926535897932384626…
1.01001000100001…
(两个1之间依次多一个0)
无限不循环小数叫做无理数.
=1.4142135623709504880168…
有些数不可以写成有限小数和无限循环小数的形式,如:
它们是无限不循环小数.
三、自主学习
我们常见的无理数有以下三种形式:
(1)含 的一些数;
(2)含开不尽方的数;
(3)无限不循环的小数,如1.01001000100001…
要点归纳:
三、自主学习
思考:你能给实数分类吗?
(1)按定义分
有理数
无理数
实数
正无理数
负无理数
正有理数
负有理数
零
有限小数或无限循环小数
无限不循环小数
知识点二 实数的概念和分类
我们将有理数和无理数统称为实数.
三、自主学习
(2)按性质分
正实数
负实数
0
实数
分类时要注意什么
不重不漏原则
四、合作探究
探究一 区分有理数和无理数
活动把下列各数分别填入相应的括号内:
0.101,
有理数
无理数
...
...
四、合作探究
练一练
1.判断下列数哪些是有理数?哪些是无理数?
有理数是:
1.23,
..
无理数是:
1.232232223...(两个3之间依次多一个2).
四、合作探究
探究二 实数的分类
活动:把下列各数填入相应的集合内.
(1)有理数集合:{ …};
(2)无理数集合:{ …};
(3)正实数集合:{ …};
(4)负实数集合:{ …}.
四、合作探究
练一练
3,
-3,
0,
π,
3,
探究二 循环小数化为分数
四、合作探究
问题提出:我们知道任何循环小数都能化为分数,那么循环小数如何
化为分数呢?
我们把循环小数分为纯循环小数例如 ,和混循环小数例如 .
问题探究1:纯循环小数化成分数
.
..
.
...
——.
( )
( )
( )
( )
5
21
999
212
根据提示完成下列的填空,并用计算器检验.
四、合作探究
.
..
.
...
观察转化结果,根据你的猜想完成下面结论.
结论1:纯循环小数转化为分数:
每个循环节有几位数字,分数的分母中就有几个 ;
分子则是 .
9
一个循环节的数
四、合作探究
问题探究2:混循环小数化成分数
用计算器检验下列转化是否正确.
.
..
...
观察转化步骤,根据你的猜想完成下面结论.
结论2:混循环小数转化为分数:
每个循环节都有几位数字,分数的分母中就有几个 ,不循环的部分有几位数字,分母中9的后面就有几个 ;
分子则是第一个循环节及它前面的数减去 .
9
0
不循环部分
四、合作探究
练一练
3.将下列循环小数化为分数.
.
.
..
. .
解:
.
.
..
. .
五、当堂检测
1.判断题:
①实数不是有理数就是无理数.( )
③无理数都是无限小数.( )
④带根号的数都是无理数.( )
⑤无理数一定都带根号.( )
⑥两个无理数之积不一定是无理数.( )
⑦两个无理数之和一定是无理数.( )
⑧数轴上的任何一点都可以表示实数.( )
×
×
×
②无理数都是无限不循环小数.( )
√
√
√
√
√
五、当堂检测
2.下列各数中,哪些是有理数?哪些是无理数?
(相邻两个1之间0的个数逐次加1).
解: 是有理数;
π+2, 0.10100100001...是无理数.
五、当堂检测
3.把下列各数分别填入相应的括号内:
(相邻两个3之间的7的个数逐次加1)
有理数
无理数
0,
0.3737737773...,
π,
六、课堂总结
无理数
带省略号且不循环的小数
有特殊意义的数,如π等
带根号,但被开方数是开方不尽的数
概念
实数
有理数
无限不循环小数
