第六章 6.4.3.1余弦定理 课件(共25张PPT)
文档属性
| 名称 | 第六章 6.4.3.1余弦定理 课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-18 17:13:49 | ||
图片预览








文档简介
(共25张PPT)
第六章
6.4 平面向量的应用
6.4.3.1 余弦定理
人教A版(2019)
教学目标
学习目标 数学素养
1.会用借助向量运算,推导余弦定理. 1.数学运算素养.
2.掌握余弦定理及其变形推论. 2.数学抽象素养.
3.会用余弦定理解决解三角形问题. 3.逻辑推理素养、数学运算素养.
温故知新
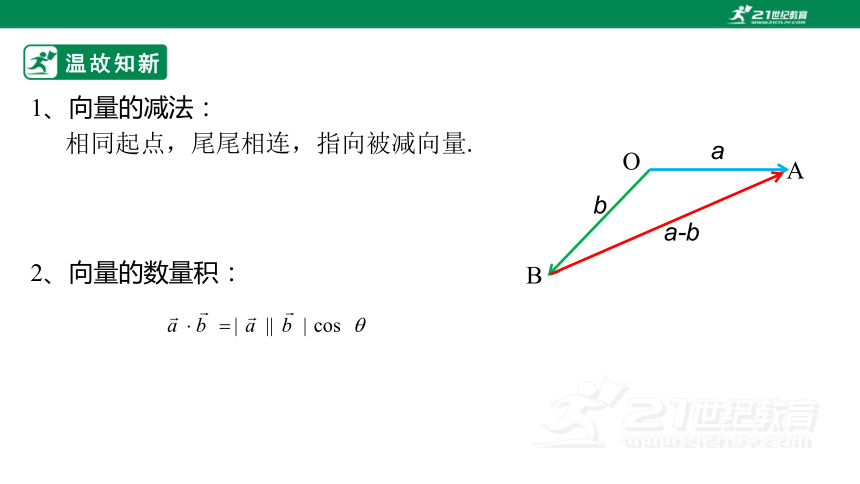
1、向量的减法:
相同起点,尾尾相连,指向被减向量.
b
B
A
O
a
a-b
2、向量的数量积:
知新引入
一个三角形含有各种各样的几何量,例如三边边长、三个内角的度数、面积等,它们之间存在着确定的关系.例如,在初中,我们得到过勾股定理、锐角三角函数,这是直角三角形中的边、角定量关系.对于一般三角形,我们已经定性的研究过三角形的边、角关系,得到了SSS、SAS、ASA、AAS等判定三角形全等的方法.这些判定方法表明,给定三角形的三个角、三条边这六个元素中的某些元素,这个三角形就是唯一确定的.那么三角形的其它元素与给定的某些元素有怎样的数量关系?
A
B
C
500m
120°
300m
b
a
c=?
西成高铁路线规划要经过一座小山丘,就需要挖隧道,从而涉及到一个问题,就是要测量出山脚的长度.而两山脚之间的距离是没有办法直接测量的,那要怎样才能知道山脚的长度呢?
知新探究
我们知道,两边和它们的夹角分别相等的两个三角形全等.这说明,给定两边及其夹角的三角形是唯一确定的.也就是说,三角形的其他边、角都可以用这两边及其夹角来表示.那么,表示的公式是什么?
在△ABC中,三个角A、B、C所对的边分别是a、b、c,怎样用a、b和C表示c?
b
c=?
a
因为涉及的是三角形的两边长(a和b)和它们的夹角(C),所以我们可以考虑用向量的数量积公式来研究.
知新探究
在△ABC中,三个角A、B、C所对的边分别是a、b、c,怎样用a、b和C表示c?
推导一
c
b
a
如图,
∴
.
.
则
思考:三角形中有别的数量关系吗?能否用a、c和角B表示b?
余弦定理
知新探究
c
b
a
注意观察,这三个式子有什么共同特点吗?
余弦定理
新知探究
余弦定理 (cosine theorem) 三角形中任何一边的平方,等于其他两边的平方的和减去这两边与它们的夹角的余弦的积的两倍. 即
b
c
a
你能用其它方法证明余弦定理吗?
余弦定理
利用余弦定理,我们可以从三角形已知的两边及其夹角直接求出第三边.
新知探究
推导二
在ΔABC中,内角A,B,C所对的边分别为如图以点A为坐标原点,边AB所在直线为轴,建立平面直角坐标系,则A(0,0),B(,0),C(),
()
由两点间距离公式,得
即
同理可证 ,.
余弦定理
新知探究
推导三
则
同理可证 ,.
余弦定理
C
①当ΔABC为锐角三角形时,如图,过顶点C作CD⊥AB于点D,则
在RtΔBCD中,由勾股定理得BC2=CD2+BD2,
即
新知探究
推导三
则
同理可证 ,.
余弦定理
②当ΔABC为直角三角形时,同理可证.
即
③当ΔABC为钝角三角形时,如图,过顶点C作CD⊥AB,交AB的延长线与点D,则
在RtΔBCD中,由勾股定理得BC2=CD2+BD2,
新知探究
余弦定理的推论
余弦定理指出了三角形的三条边与其中的一个角之间的关系,应用余弦定理,我们可以解决已知三角形的三边确定三角形的角的问题,怎么确定呢?
b
c
a
余弦定理及其推论把用“SAS”和“SSS”判定三角形全等的方法从数量化的角度进行了刻画.
利用余弦定理的推论,可以由三角形的三边直接计算出三角形的三个角.
从余弦定理及其推论可以看出,三角函数把几何中关于三角形的定性结论变成了可定量计算的公式.
新知探究
余弦定理的推论
勾股定理指出了直角三角形中三边之间的关系,余弦定理则指出了三角形的三条边与其中的一个角之间的关系.你能说说这两个定理之间的关系吗?
一般地,三角形的三个角A,B,C和它们的对边a,b,c叫做三角形的元素.已知三角形的几个元素求其他元素的过程叫做解三角形(solving a triangle).
如果△ABC中有一个角是直角,例如,当C=90°,这时,由余弦定理可得,,这就是勾股定理.由此可见,余弦定理是勾股定理的推广,勾股定理是余弦定理的特例.
新知探究
【例1】在△ABC 中,已知b=60 cm,c=34 cm,A=41°,解这个三角形 (角度精确到1°,边长精确到1 cm).
解:
由余弦定理,得
≈1676.78
∴(cm)
由余弦定理的推论,得
,
利用计算器,得B≈106°,
∴C=180°-(A+B)≈180°-(41°+106°)=33°.
初试身手
1.在△ABC中,已知a=300m,b=500m,C=120°,求c.
解:
=300 +500 -2×300×500×cos120°
=490000
∴(m).
A
B
C
500m
120°
300m
b
a
c=?
由余弦定理,得
新知探究
【例2】在△ABC中,,锐角C满足,求B(精确到1°).
解:
∵,且C为锐角,
∴
由余弦定理,得
=9
∴c=3
分析:由条件可求,再利用余弦定理及其推论可求出B的值.
∴,
利用计算器,可得 B≈98°.
初试身手
由余弦定理,可得
2.在ΔABC中,内角A,B,C所对的边分别是,且°,求.
解:
∴ ,或(舍去)
∴A=30°,B=180°-(A+C)=135°.
则A=30°,B=135°, .
∵ 且0<A<180°,
∵
新知探究
∵,
解:
由余弦定理,得
,
整理得,.
【例3】在△ABC中,角A,B,C的对边分别为若,试判断△ABC的形状.
即,
∴,
∴.
则△ABC为直角三角形或等腰三角形.
新知探究
初试身手
在△ABC中,由已知,得
3.在△ABC中,角A,B,C的对边分别为已知,试判断△ABC的形状.
解:
∴,即.
根据余弦定理,得
则△ABC是直角三角形.
,即.
,
课堂小结
1.余弦定理的推导
①向量法; ②坐标法; ③几何法.
2.余弦定理及其推论
3.利用余弦定理解三角形
①已知两边和夹角求第三边;
②已知三边求三角;
③判断三角形形状.
作业布置
作业: P52-54 习题6.4 第6,15,16题.
补充:
1.(多选)设△ABC的内角A,B,C的对边分别为a,b,c.若a=2,c=2,cos A=,且bA.b=2 B.b=2 C.B=60° D.B=30°
2.已知在△ABC中,bcos A=acos B,则△ABC是( )
A.等边三角形 B.等腰三角形 C.直角三角形 D.锐角三角形.
3.(多选)在△ABC中,若(a2+c2-b2)tanB=ac,则角B的可能值为( )
A. B. C. D.
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
第六章
6.4 平面向量的应用
6.4.3.1 余弦定理
人教A版(2019)
教学目标
学习目标 数学素养
1.会用借助向量运算,推导余弦定理. 1.数学运算素养.
2.掌握余弦定理及其变形推论. 2.数学抽象素养.
3.会用余弦定理解决解三角形问题. 3.逻辑推理素养、数学运算素养.
温故知新
1、向量的减法:
相同起点,尾尾相连,指向被减向量.
b
B
A
O
a
a-b
2、向量的数量积:
知新引入
一个三角形含有各种各样的几何量,例如三边边长、三个内角的度数、面积等,它们之间存在着确定的关系.例如,在初中,我们得到过勾股定理、锐角三角函数,这是直角三角形中的边、角定量关系.对于一般三角形,我们已经定性的研究过三角形的边、角关系,得到了SSS、SAS、ASA、AAS等判定三角形全等的方法.这些判定方法表明,给定三角形的三个角、三条边这六个元素中的某些元素,这个三角形就是唯一确定的.那么三角形的其它元素与给定的某些元素有怎样的数量关系?
A
B
C
500m
120°
300m
b
a
c=?
西成高铁路线规划要经过一座小山丘,就需要挖隧道,从而涉及到一个问题,就是要测量出山脚的长度.而两山脚之间的距离是没有办法直接测量的,那要怎样才能知道山脚的长度呢?
知新探究
我们知道,两边和它们的夹角分别相等的两个三角形全等.这说明,给定两边及其夹角的三角形是唯一确定的.也就是说,三角形的其他边、角都可以用这两边及其夹角来表示.那么,表示的公式是什么?
在△ABC中,三个角A、B、C所对的边分别是a、b、c,怎样用a、b和C表示c?
b
c=?
a
因为涉及的是三角形的两边长(a和b)和它们的夹角(C),所以我们可以考虑用向量的数量积公式来研究.
知新探究
在△ABC中,三个角A、B、C所对的边分别是a、b、c,怎样用a、b和C表示c?
推导一
c
b
a
如图,
∴
.
.
则
思考:三角形中有别的数量关系吗?能否用a、c和角B表示b?
余弦定理
知新探究
c
b
a
注意观察,这三个式子有什么共同特点吗?
余弦定理
新知探究
余弦定理 (cosine theorem) 三角形中任何一边的平方,等于其他两边的平方的和减去这两边与它们的夹角的余弦的积的两倍. 即
b
c
a
你能用其它方法证明余弦定理吗?
余弦定理
利用余弦定理,我们可以从三角形已知的两边及其夹角直接求出第三边.
新知探究
推导二
在ΔABC中,内角A,B,C所对的边分别为如图以点A为坐标原点,边AB所在直线为轴,建立平面直角坐标系,则A(0,0),B(,0),C(),
()
由两点间距离公式,得
即
同理可证 ,.
余弦定理
新知探究
推导三
则
同理可证 ,.
余弦定理
C
①当ΔABC为锐角三角形时,如图,过顶点C作CD⊥AB于点D,则
在RtΔBCD中,由勾股定理得BC2=CD2+BD2,
即
新知探究
推导三
则
同理可证 ,.
余弦定理
②当ΔABC为直角三角形时,同理可证.
即
③当ΔABC为钝角三角形时,如图,过顶点C作CD⊥AB,交AB的延长线与点D,则
在RtΔBCD中,由勾股定理得BC2=CD2+BD2,
新知探究
余弦定理的推论
余弦定理指出了三角形的三条边与其中的一个角之间的关系,应用余弦定理,我们可以解决已知三角形的三边确定三角形的角的问题,怎么确定呢?
b
c
a
余弦定理及其推论把用“SAS”和“SSS”判定三角形全等的方法从数量化的角度进行了刻画.
利用余弦定理的推论,可以由三角形的三边直接计算出三角形的三个角.
从余弦定理及其推论可以看出,三角函数把几何中关于三角形的定性结论变成了可定量计算的公式.
新知探究
余弦定理的推论
勾股定理指出了直角三角形中三边之间的关系,余弦定理则指出了三角形的三条边与其中的一个角之间的关系.你能说说这两个定理之间的关系吗?
一般地,三角形的三个角A,B,C和它们的对边a,b,c叫做三角形的元素.已知三角形的几个元素求其他元素的过程叫做解三角形(solving a triangle).
如果△ABC中有一个角是直角,例如,当C=90°,这时,由余弦定理可得,,这就是勾股定理.由此可见,余弦定理是勾股定理的推广,勾股定理是余弦定理的特例.
新知探究
【例1】在△ABC 中,已知b=60 cm,c=34 cm,A=41°,解这个三角形 (角度精确到1°,边长精确到1 cm).
解:
由余弦定理,得
≈1676.78
∴(cm)
由余弦定理的推论,得
,
利用计算器,得B≈106°,
∴C=180°-(A+B)≈180°-(41°+106°)=33°.
初试身手
1.在△ABC中,已知a=300m,b=500m,C=120°,求c.
解:
=300 +500 -2×300×500×cos120°
=490000
∴(m).
A
B
C
500m
120°
300m
b
a
c=?
由余弦定理,得
新知探究
【例2】在△ABC中,,锐角C满足,求B(精确到1°).
解:
∵,且C为锐角,
∴
由余弦定理,得
=9
∴c=3
分析:由条件可求,再利用余弦定理及其推论可求出B的值.
∴,
利用计算器,可得 B≈98°.
初试身手
由余弦定理,可得
2.在ΔABC中,内角A,B,C所对的边分别是,且°,求.
解:
∴ ,或(舍去)
∴A=30°,B=180°-(A+C)=135°.
则A=30°,B=135°, .
∵ 且0<A<180°,
∵
新知探究
∵,
解:
由余弦定理,得
,
整理得,.
【例3】在△ABC中,角A,B,C的对边分别为若,试判断△ABC的形状.
即,
∴,
∴.
则△ABC为直角三角形或等腰三角形.
新知探究
初试身手
在△ABC中,由已知,得
3.在△ABC中,角A,B,C的对边分别为已知,试判断△ABC的形状.
解:
∴,即.
根据余弦定理,得
则△ABC是直角三角形.
,即.
,
课堂小结
1.余弦定理的推导
①向量法; ②坐标法; ③几何法.
2.余弦定理及其推论
3.利用余弦定理解三角形
①已知两边和夹角求第三边;
②已知三边求三角;
③判断三角形形状.
作业布置
作业: P52-54 习题6.4 第6,15,16题.
补充:
1.(多选)设△ABC的内角A,B,C的对边分别为a,b,c.若a=2,c=2,cos A=,且b
2.已知在△ABC中,bcos A=acos B,则△ABC是( )
A.等边三角形 B.等腰三角形 C.直角三角形 D.锐角三角形.
3.(多选)在△ABC中,若(a2+c2-b2)tanB=ac,则角B的可能值为( )
A. B. C. D.
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
