2.3确定二次函数的表达式 课件(共26张PPT)2023-2024学年度北师大版数学九年级下册
文档属性
| 名称 | 2.3确定二次函数的表达式 课件(共26张PPT)2023-2024学年度北师大版数学九年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 328.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-17 11:30:39 | ||
图片预览








文档简介
(共26张PPT)
2.3 确定二次函数的表达式
九年级下
北师版
1. 会用待定系数法求二次函数的解析式.
2. 能灵活运用二次函数的不同形式求函数解析式.
学习目标
难点
重点
我们学过的二次函数解析式都有哪些?
新课引入
y=ax2(a≠0)
y=ax2+k(a≠0)
y=a(x-h)2(a≠0)
y=a(x-h)2+k(a≠0)
y = ax2+bx+c(a≠0)
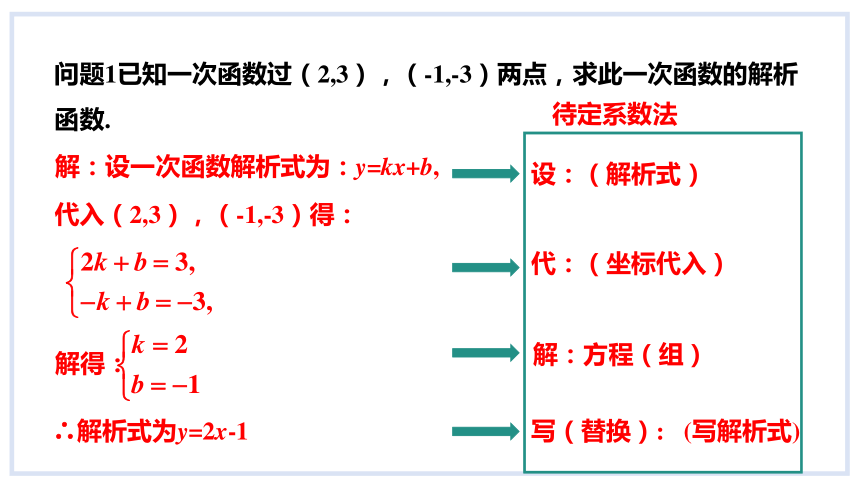
问题1已知一次函数过(2,3),(-1,-3)两点,求此一次函数的解析函数.
写(替换): (写解析式)
解:设一次函数解析式为:y=kx+b,
待定系数法
设:(解析式)
代:(坐标代入)
解得:
解:方程(组)
∴解析式为y=2x-1
代入(2,3),(-1,-3)得:
1.一次函数y=kx+b(k≠0)需要待定的系数是什么?通常需要已知几个点的坐标求出它的解析式?
2.求一次函数解析式的方法是什么?它的一般步骤是什么?
k、b
2个
待定系数法: (1)设:(解析式)
(2)代:(坐标代入)
(3)解:方程(组)
(4)写(替换):(写解析式)
思考
例1 已知二次函数y=ax2 + c(a≠0)的图象经过点(2,3)和(-1,-3),求这个二次函数的表达式.
解:∵将点(2,3)和(-1,-3)的坐标分别带入表达式y=ax2+c,得
∴所求二次函数表达式为 y=2x2-5.
a=2,
c=-5.
解得
{
∴
3=4a+c,
-3=a+c,
{
新知学习
一、一般式求二次函数表达式
如果改变题目条件,将二次函数表达式换为y=ax2 +bx+c(a≠0),能求出来吗?
探究
由几个点的坐标可以确定二次函数?
由两点(两点的连线不与坐标轴平行)的坐标可以确定一次函数,即可以求出这个一次函数的解析式.类似地,由不在同一直线上的三点(任意两点的连线不与y轴平行)的坐标,可以确定二次函数的解析式.
例2 如果一个二次函数的图象经过( -1,10 ),( 1,4 ),( 2,7 )三点,能求出这个二次函数的解析式吗?如果能,求出这个二次函数的解析式.
所求二次函数解析式为 y=2x2-3x+5.
解:设所求二次函数的解析式为 y=ax2+bx+c.
由已知,图象经过( -1,10 ),( 1,4 ),( 2,7 ) 三点,得关于a,b,c的三元一次方程组
解得
归纳
这种已知三点求二次函数表达式的方法叫做一般式法.
其步骤是:
①设函数表达式为 y=ax2+bx+c(a≠0);
②代入后得到一个三元一次方程组;
③解方程组得到 a,b,c 的值;
④把待定系数用数字换掉,写出函数表达式.
针对训练
1.已知二次函数y=ax2 + bx的图象经过点(-2,8)和(-1,5),求这个二次函数的表达式.
解:∵该图象经过点(-2,8)和(-1,5),
∴ y=-x2-6x.
8=4a-2b,
5=a-b,
∴
{
解得
{
a=-1,
b=-6.
图象经过原点
(c=0)
解: 设这个二次函数的表达式是 y=ax2+bx+c,
由于这个函数经过点( 0,1 ),可得c=1.
又由于其图象经过( 2,4 )、( 3,10 )两点,可得
4a+2b+1=4,
9a+3b+1=10,
∴所求的二次函数的表达式是
解得
2.一个二次函数的图象经过 ( 0,1 )、( 2,4 )、( 3,10 )三点,求这个二次函数的表达式.
在什么情况下,已知二次函数图象上两点的坐标就可以确定它的表达式?
顶点坐标和图象上另一点坐标.
已知二次函数y=ax2+bx+c(a≠0)中一项系数,再知道图象上两点的坐标,可以确定它的表达式
思考
例2 一名学生推铅球时, 铅球行进高度y(m)与水平距离x(m)之间的关系如图所示,其中(4,3)为图象的顶点,你能求出y与x之间的关系式吗
解:根据图象是一条抛物线且顶点坐标为(4,3),因此设它
的关系式为y=a(x-4)2+3
又∵图象过点(10,0)
∴a(10-4)2+3=0
二、利用顶点式求二次函数的表达式
归纳
这种知道抛物线的顶点坐标,求表达式的方法叫做顶点式法.
其步骤是:
①设函数表达式是 y=a(x-h)2+k(a≠0);
②先代入顶点坐标,得到关于a的一元一次方程;
③将另一点的坐标代入原方程求出a值;
④a 用数值换掉,写出函数表达式.
针对训练
1.一个二次函数的图象经点( 0,1 ),它的顶点坐标为( 8,9 ),求这个二次函数的表达式.
解: 因为这个二次函数的图象的顶点坐标为(8,9),因此,可以设函数表达式为 y = a(x-8)2+9.
又由于它的图象经过点 (0,1),可得 1=a(0-8) +9.
解得 a=
∴所求的二次函数的解析式是
2. 已知二次函数 y=a(x-2)2+18的图象经过点( -1,0 ).求这个二次函数的解析式.
则函数解析式为 y = -2(x-1)2+18.
解:把 (-1,0) 代入二次函数解析式得 9a+18 = 0,
即 a = -2,
例4 已知抛物线 y=ax2+bx+c 与 x 轴交于点A( 1,0 ),B( 5,0 ),且过点 C( 0,-5 ).求抛物线的解析式.
解:C( 0,-5 )代入y=ax2+bx+c中
得c=5,
∴ y=ax2+bx+5 ,将点A( 1,0 ),B( 5,0 )代入
得
即y=-x2+6x-5.
a+b+5=0,
25a+5b+5=0,
解得
还有其他方法吗?
三、利用交点式求二次函数的表达式
例4 已知抛物线 y=ax2+bx+c 与 x 轴交于点A( 1,0 ),B( 5,0 ),且过点 C( 0,-5 ).求抛物线的解析式.
A( 1,0 ),B( 5,0 )
图象的对称性
对称轴为x=3
y=a(x-3)2+k
代入A( 1,0 ),B( 5,0 )
求出a,k
化为一般式
y=ax2-6ax+3
代入A( 1,0 ),B( 5,0 )
求出a,b
例4 已知抛物线 y=ax2+bx+c 与 x 轴交于点A( 1,0 ),B( 5,0 ),且过点 C( 0,-5 ).求抛物线的解析式.
解:∵抛物线与x轴交于点 A( 1,0 ),B( 5,0 ),
∴可设抛物线解析式为 y=a(x-1)(x-5),
把( 0,-5 )代入得:5a=-5,解得,a=-1,
故抛物线的解析式为y=-(x-1)(x-5),
即y=-x2+6x-5.
y=a(x-x1)(x-x2)叫做交点式
归纳
这种知道抛物线的与x, y轴的交点坐标,求表达式的方法叫做交点式法.
其步骤是:
①设函数表达式是y=a(x-x1)(x-x2)(a≠0);
②先代入交点坐标,得到关于a的一元一次方程;
③将另一点的坐标代入原方程求出a值;
④a用数值换掉,写出函数表达式.
x1, x2表示函数与x轴交点的横坐标.
针对训练
1.二次函数的图象经过点A(1,0),B(0,-3),对称轴是直线 x = 2,求该二次函数的解析式.
解:∵图象经过点 A(1,0),对称轴是直线 x = 2,
∴图象经过另一点( 3,0 ).
∴设该二次函数的解析式为y=a(x-1)(x-3).
将点( 0,-3 )代入,得
-3=a·(-1)(-3)
解得
a = -1.
∴该二次函数的解析式为 y = -(x-1)(x-3) = -x2+4x-3.
随堂练习
1.如图,若抛物线y=ax2+2x+a2-1经过原点,则抛物线的解析式为( )
A. y=-x2+2x
B. y=x2+2x
C. y=-x2+2x+1
D. y=-x2+2x或y=x2+2x
A
2.二次函数 的顶点为 ,图象与 轴交于点 ,则 的面积为( @16@ )
A. B. C. D.
B
3.已知抛物线 交 轴于 , 两点,若抛物线上有且只有 , , 三点满足 ,则 的值为____.
1
3. 如图,抛物线 y=x2+bx+c 过点 A(-4,-3),与 y 轴交于点 B,对称轴是 x=-3,请解答下列问题:
(1) 求抛物线的解析式;
x
y
O
x = -3
A
B
解:把点 A (-4,-3) 代入 y=x2+bx+c,
得 16-4b+c =-3,即 c=4b-19.
∵ 对称轴是 x=-3,∴ =-3,
即 b=6. ∴ c=5.
∴ 抛物线的解析式是 y = x2+6x+5.
x
y
O
x = -3
A
B
(2) 若和 x 轴平行的直线与抛物线交于 C,D 两点,点 C 在对称轴左侧,且 CD=8,求△BCD 的面积.
解:∵ CD∥x 轴,∴ 点 C 与点 D 关于 x=-3 对称.
∵ 点 C 在对称轴左侧,且 CD=8,
∴ 点 C 的横坐标为-7.
∴ 点 C 的纵坐标为 (-7)2+6×(-7)+5=12.
∵ 点 B 的坐标为 (0,5),
∴ △BCD 中 CD 边上的高为 12-5=7.
∴ △BCD 的面积为 ×8×7=28.
用待定系数法求二次函数解析式的步骤
1. 设: 根据题中已知条件, 合理设出二次函数的解析式, 如
y = ax2+bx+c 或 y = a(x-h)2+k 或 y = a(x-x1)(x-x2),其中 a ≠ 0;
2. 代:把已知点的坐标代入所设的二次函数解析式中,得到关于解析式中待定系数的方程(组);
3. 解:解此方程或方程组,求出a,b,c的值;
4. 替换:将所设的解析式中的a、b、c用求出的具体数字替换到解析式中,求得解析式.
课堂小结
2.3 确定二次函数的表达式
九年级下
北师版
1. 会用待定系数法求二次函数的解析式.
2. 能灵活运用二次函数的不同形式求函数解析式.
学习目标
难点
重点
我们学过的二次函数解析式都有哪些?
新课引入
y=ax2(a≠0)
y=ax2+k(a≠0)
y=a(x-h)2(a≠0)
y=a(x-h)2+k(a≠0)
y = ax2+bx+c(a≠0)
问题1已知一次函数过(2,3),(-1,-3)两点,求此一次函数的解析函数.
写(替换): (写解析式)
解:设一次函数解析式为:y=kx+b,
待定系数法
设:(解析式)
代:(坐标代入)
解得:
解:方程(组)
∴解析式为y=2x-1
代入(2,3),(-1,-3)得:
1.一次函数y=kx+b(k≠0)需要待定的系数是什么?通常需要已知几个点的坐标求出它的解析式?
2.求一次函数解析式的方法是什么?它的一般步骤是什么?
k、b
2个
待定系数法: (1)设:(解析式)
(2)代:(坐标代入)
(3)解:方程(组)
(4)写(替换):(写解析式)
思考
例1 已知二次函数y=ax2 + c(a≠0)的图象经过点(2,3)和(-1,-3),求这个二次函数的表达式.
解:∵将点(2,3)和(-1,-3)的坐标分别带入表达式y=ax2+c,得
∴所求二次函数表达式为 y=2x2-5.
a=2,
c=-5.
解得
{
∴
3=4a+c,
-3=a+c,
{
新知学习
一、一般式求二次函数表达式
如果改变题目条件,将二次函数表达式换为y=ax2 +bx+c(a≠0),能求出来吗?
探究
由几个点的坐标可以确定二次函数?
由两点(两点的连线不与坐标轴平行)的坐标可以确定一次函数,即可以求出这个一次函数的解析式.类似地,由不在同一直线上的三点(任意两点的连线不与y轴平行)的坐标,可以确定二次函数的解析式.
例2 如果一个二次函数的图象经过( -1,10 ),( 1,4 ),( 2,7 )三点,能求出这个二次函数的解析式吗?如果能,求出这个二次函数的解析式.
所求二次函数解析式为 y=2x2-3x+5.
解:设所求二次函数的解析式为 y=ax2+bx+c.
由已知,图象经过( -1,10 ),( 1,4 ),( 2,7 ) 三点,得关于a,b,c的三元一次方程组
解得
归纳
这种已知三点求二次函数表达式的方法叫做一般式法.
其步骤是:
①设函数表达式为 y=ax2+bx+c(a≠0);
②代入后得到一个三元一次方程组;
③解方程组得到 a,b,c 的值;
④把待定系数用数字换掉,写出函数表达式.
针对训练
1.已知二次函数y=ax2 + bx的图象经过点(-2,8)和(-1,5),求这个二次函数的表达式.
解:∵该图象经过点(-2,8)和(-1,5),
∴ y=-x2-6x.
8=4a-2b,
5=a-b,
∴
{
解得
{
a=-1,
b=-6.
图象经过原点
(c=0)
解: 设这个二次函数的表达式是 y=ax2+bx+c,
由于这个函数经过点( 0,1 ),可得c=1.
又由于其图象经过( 2,4 )、( 3,10 )两点,可得
4a+2b+1=4,
9a+3b+1=10,
∴所求的二次函数的表达式是
解得
2.一个二次函数的图象经过 ( 0,1 )、( 2,4 )、( 3,10 )三点,求这个二次函数的表达式.
在什么情况下,已知二次函数图象上两点的坐标就可以确定它的表达式?
顶点坐标和图象上另一点坐标.
已知二次函数y=ax2+bx+c(a≠0)中一项系数,再知道图象上两点的坐标,可以确定它的表达式
思考
例2 一名学生推铅球时, 铅球行进高度y(m)与水平距离x(m)之间的关系如图所示,其中(4,3)为图象的顶点,你能求出y与x之间的关系式吗
解:根据图象是一条抛物线且顶点坐标为(4,3),因此设它
的关系式为y=a(x-4)2+3
又∵图象过点(10,0)
∴a(10-4)2+3=0
二、利用顶点式求二次函数的表达式
归纳
这种知道抛物线的顶点坐标,求表达式的方法叫做顶点式法.
其步骤是:
①设函数表达式是 y=a(x-h)2+k(a≠0);
②先代入顶点坐标,得到关于a的一元一次方程;
③将另一点的坐标代入原方程求出a值;
④a 用数值换掉,写出函数表达式.
针对训练
1.一个二次函数的图象经点( 0,1 ),它的顶点坐标为( 8,9 ),求这个二次函数的表达式.
解: 因为这个二次函数的图象的顶点坐标为(8,9),因此,可以设函数表达式为 y = a(x-8)2+9.
又由于它的图象经过点 (0,1),可得 1=a(0-8) +9.
解得 a=
∴所求的二次函数的解析式是
2. 已知二次函数 y=a(x-2)2+18的图象经过点( -1,0 ).求这个二次函数的解析式.
则函数解析式为 y = -2(x-1)2+18.
解:把 (-1,0) 代入二次函数解析式得 9a+18 = 0,
即 a = -2,
例4 已知抛物线 y=ax2+bx+c 与 x 轴交于点A( 1,0 ),B( 5,0 ),且过点 C( 0,-5 ).求抛物线的解析式.
解:C( 0,-5 )代入y=ax2+bx+c中
得c=5,
∴ y=ax2+bx+5 ,将点A( 1,0 ),B( 5,0 )代入
得
即y=-x2+6x-5.
a+b+5=0,
25a+5b+5=0,
解得
还有其他方法吗?
三、利用交点式求二次函数的表达式
例4 已知抛物线 y=ax2+bx+c 与 x 轴交于点A( 1,0 ),B( 5,0 ),且过点 C( 0,-5 ).求抛物线的解析式.
A( 1,0 ),B( 5,0 )
图象的对称性
对称轴为x=3
y=a(x-3)2+k
代入A( 1,0 ),B( 5,0 )
求出a,k
化为一般式
y=ax2-6ax+3
代入A( 1,0 ),B( 5,0 )
求出a,b
例4 已知抛物线 y=ax2+bx+c 与 x 轴交于点A( 1,0 ),B( 5,0 ),且过点 C( 0,-5 ).求抛物线的解析式.
解:∵抛物线与x轴交于点 A( 1,0 ),B( 5,0 ),
∴可设抛物线解析式为 y=a(x-1)(x-5),
把( 0,-5 )代入得:5a=-5,解得,a=-1,
故抛物线的解析式为y=-(x-1)(x-5),
即y=-x2+6x-5.
y=a(x-x1)(x-x2)叫做交点式
归纳
这种知道抛物线的与x, y轴的交点坐标,求表达式的方法叫做交点式法.
其步骤是:
①设函数表达式是y=a(x-x1)(x-x2)(a≠0);
②先代入交点坐标,得到关于a的一元一次方程;
③将另一点的坐标代入原方程求出a值;
④a用数值换掉,写出函数表达式.
x1, x2表示函数与x轴交点的横坐标.
针对训练
1.二次函数的图象经过点A(1,0),B(0,-3),对称轴是直线 x = 2,求该二次函数的解析式.
解:∵图象经过点 A(1,0),对称轴是直线 x = 2,
∴图象经过另一点( 3,0 ).
∴设该二次函数的解析式为y=a(x-1)(x-3).
将点( 0,-3 )代入,得
-3=a·(-1)(-3)
解得
a = -1.
∴该二次函数的解析式为 y = -(x-1)(x-3) = -x2+4x-3.
随堂练习
1.如图,若抛物线y=ax2+2x+a2-1经过原点,则抛物线的解析式为( )
A. y=-x2+2x
B. y=x2+2x
C. y=-x2+2x+1
D. y=-x2+2x或y=x2+2x
A
2.二次函数 的顶点为 ,图象与 轴交于点 ,则 的面积为( @16@ )
A. B. C. D.
B
3.已知抛物线 交 轴于 , 两点,若抛物线上有且只有 , , 三点满足 ,则 的值为____.
1
3. 如图,抛物线 y=x2+bx+c 过点 A(-4,-3),与 y 轴交于点 B,对称轴是 x=-3,请解答下列问题:
(1) 求抛物线的解析式;
x
y
O
x = -3
A
B
解:把点 A (-4,-3) 代入 y=x2+bx+c,
得 16-4b+c =-3,即 c=4b-19.
∵ 对称轴是 x=-3,∴ =-3,
即 b=6. ∴ c=5.
∴ 抛物线的解析式是 y = x2+6x+5.
x
y
O
x = -3
A
B
(2) 若和 x 轴平行的直线与抛物线交于 C,D 两点,点 C 在对称轴左侧,且 CD=8,求△BCD 的面积.
解:∵ CD∥x 轴,∴ 点 C 与点 D 关于 x=-3 对称.
∵ 点 C 在对称轴左侧,且 CD=8,
∴ 点 C 的横坐标为-7.
∴ 点 C 的纵坐标为 (-7)2+6×(-7)+5=12.
∵ 点 B 的坐标为 (0,5),
∴ △BCD 中 CD 边上的高为 12-5=7.
∴ △BCD 的面积为 ×8×7=28.
用待定系数法求二次函数解析式的步骤
1. 设: 根据题中已知条件, 合理设出二次函数的解析式, 如
y = ax2+bx+c 或 y = a(x-h)2+k 或 y = a(x-x1)(x-x2),其中 a ≠ 0;
2. 代:把已知点的坐标代入所设的二次函数解析式中,得到关于解析式中待定系数的方程(组);
3. 解:解此方程或方程组,求出a,b,c的值;
4. 替换:将所设的解析式中的a、b、c用求出的具体数字替换到解析式中,求得解析式.
课堂小结
