3.1圆 课件(共30张PPT)2023-2024学年度北师大版数学九年级下册
文档属性
| 名称 | 3.1圆 课件(共30张PPT)2023-2024学年度北师大版数学九年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-17 11:47:43 | ||
图片预览








文档简介
(共30张PPT)
3.1 圆
九年级下
北师版
1.经历形成圆概念的过程,经历探索点与圆位置关系的过程.
2.理解圆以及与圆有关的概念,并了解它们之间的区别和联系.
3.初步了解点与圆的位置关系.
学习目标
难点
重点
一些学生正在做投圈游戏,他们的投圈目标都是图中的竹筒,他们呈“一”字排开.
问题:这样的队形对每个人都公平吗?你认为他们应当排成什么样的队形?
新课引入
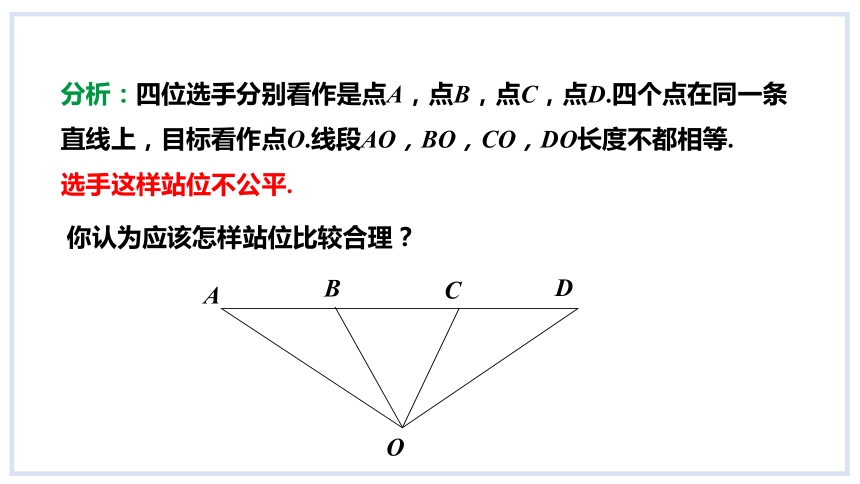
分析:四位选手分别看作是点A,点B,点C,点D.四个点在同一条直线上,目标看作点O.线段AO,BO,CO,DO长度不都相等.
选手这样站位不公平.
你认为应该怎样站位比较合理?
A
B
C
D
O
A
B
C
D
O
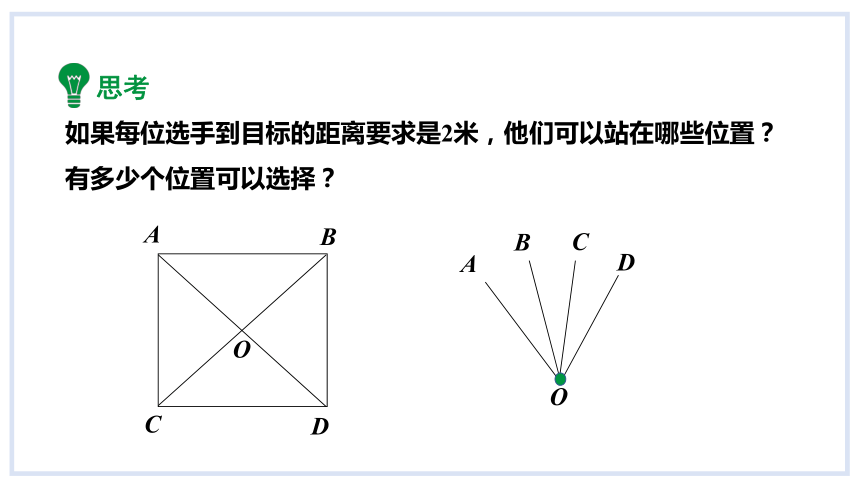
如果每位选手到目标的距离要求是2米,他们可以站在哪些位置?有多少个位置可以选择?
A
B
C
D
O
思考
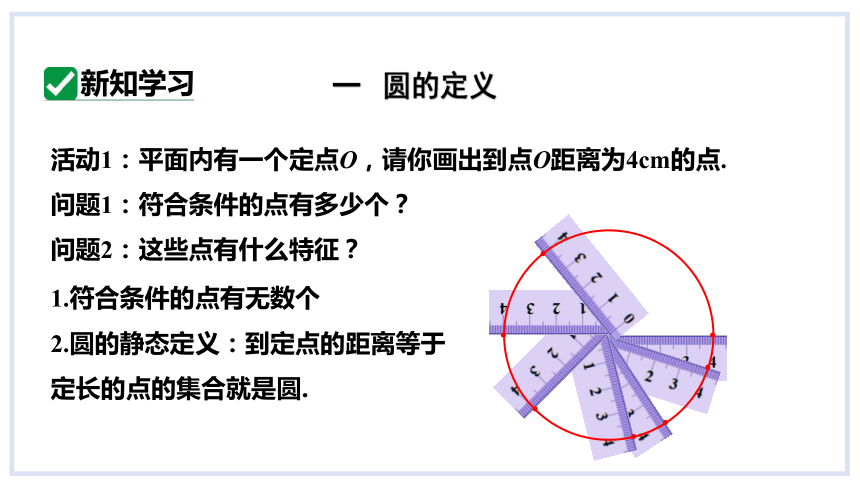
活动1:平面内有一个定点O,请你画出到点O距离为4cm的点.
问题1:符合条件的点有多少个?
问题2:这些点有什么特征?
新知学习
一 圆的定义
O
1.符合条件的点有无数个
2.圆的静态定义:到定点的距离等于定长的点的集合就是圆.
·
r
O
A
问题3:如图,线段 OA 绕它固定的一个端点 O 旋转一周,另一个端点 A 路径是什么?
2cm
3. 圆的动态定义:在一个平面内,线段 OA 绕一个端点 O 旋转一周,端点 A 所经过的路径叫做圆.其固定的端点 O 叫做圆心,线段 OA 叫做半径. 以点 O为圆心的圆,记作⊙O,读作“圆O”.
想一想,从画圆的过程可以看出什么呢?
(1)圆上各点到定点(圆心O)的距离都等于 .
(2)到定点的距离等于定长的点都在 .
定长r
同一个圆上
圆的集合定义:圆可以看成是平面上到定点的距离等于定长的所有点组成的图形.定点就是圆心,定长就是半径.
1.画一个圆,需要几个要素?
2.圆有什么特征?
思考
确定一个圆需要“两个要素”,一是圆心:圆心定其位置,二是半径:半径定其大小.
圆是一条封闭的曲线,曲线是“圆周”,而不能认为是“圆面”.
问题:现在你能回答本课最开始的问题了吗?
你认为他们应当排成什么样的队形?
为了使游戏公平,这些学生应以竹筒为圆心,以某一名同学到竹筒的距离为半径围成一个圆,因为圆上各点到圆心的距离都等于半径.
针对训练
1.下列关于圆的叙述正确的是( )
A.圆是由圆心唯一确定的
B.圆是一条封闭的曲线
C.到定点的距离小于或等于定长的所有点组成圆
D.圆内任意一点到圆心的距离都相等
B
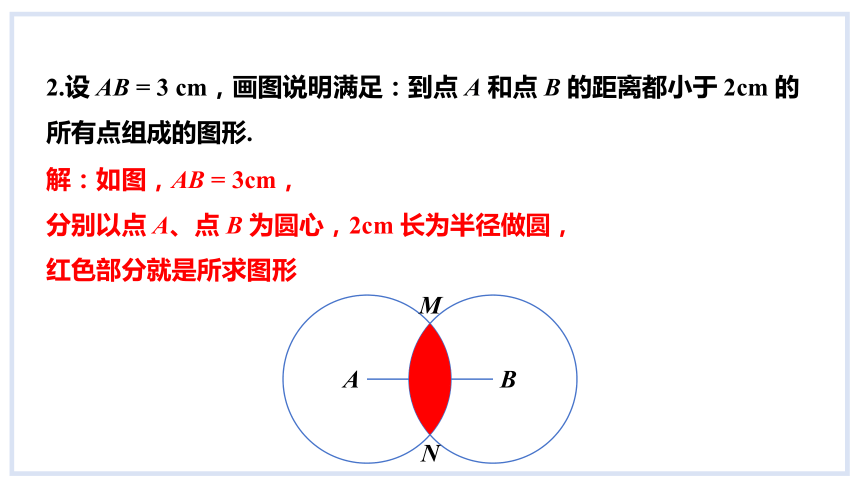
2.设 AB = 3 cm,画图说明满足:到点 A 和点 B 的距离都小于 2cm 的所有点组成的图形.
解:如图,AB = 3cm,
分别以点 A、点 B 为圆心,2cm 长为半径做圆,
红色部分就是所求图形
A
B
M
N
2.矩形ABCD 的对角线AC,BD相交于点O.求证:A,B,C,D 四个点在以点O为圆心的同一个圆上.
证明:∵四边形ABCD为矩形,
∴OA=OC=AC,OB=OD=BD,AC=BD.
∴OA=OC=OB=OD.
∴A,B,C,D四个点在以点O为圆心,OA为半径的
圆上.
A
B
C
D
O
A,B,C,D四点到圆心O的距离相等
变式:以 AB 为斜边,做一个直角三角形 ABC,求满足条件的所有点 C 组成的图形.
解:以 AB 为斜边,作直角三角形,取AB中点O,
由直角三角形斜边上的中线是斜边的一半可知,
OC = AB,
即OC的长为定值,
∴点C组成的图形为以AB重点O为圆心,OA长为半径的圆.
二 与圆有关的概念
C
A
·
O
B
连接圆上任意两点的线段(如图中的AC)叫做弦.
经过圆心的弦(如图中的AB)叫做直径.
探究
圆中最长的弦是什么?
O
B
O
A
B
O
A
B
O
A
B
C
O
A
B
C
D
O
A
B
C
D
圆中最长的弦是直径.
证明思路:三角形的三边关系可判断.
注意:1.弦和直径都是线段.
2.直径是经过圆心的特殊的弦,是圆中最长的弦,但弦不一定是直径.
·
C
O
A
B
半圆:圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆.
·
C
O
A
B
弧:圆上任意两点间的部分叫做圆弧,简称弧.以A、B为端点的弧记作 AB ,读作“圆弧AB”或“弧AB”.
(
劣弧与优弧:小于半圆的弧叫做劣弧.如图中的AC ;
(
大于半圆的弧叫做优弧.如图中的ABC.
(
能够重合的两个圆叫做等圆.
等圆
半径相同,圆心不同.
同心圆
圆心相同,半径不同。
·
C
O
A
·
C
O1
A
·
C
O
A
长度相等的弧不一定是等弧!
如图,如果AB和CD的拉直长度都是10 cm,平移并调整小圆的位置,是否能使这两条弧完全重合?
D
C
A
B
这两条弧不能完全重合,因为这两条弧半径不同,弧的弯曲程度不同. “等弧”不等于“长度相等的弧”,等弧仅仅存在于同圆或者等圆中.
在同圆或等圆中,能够互相重合的弧叫做等弧.
针对训练
1.以下命题:(1)半圆是弧,但弧不一定是半圆;(2)过圆上任意一点只能作一条弦,且这条弦是直径;(3)弦是直径;(4)直径是圆中最长的弦;(5)直径不是弦;(6)优弧大于劣弧;(7)以O为圆心可以画无数个圆. 正确的个数为( )
A.1 B.2 C.3 D.4
C
观察下图中点和圆的位置关系有哪几种?
.
o
.
.
.
.
.
.
点和圆的位置关系有三种:
点在圆内,点在圆上,点在圆外.
三 点和圆的位置关系
r
P
d
P
r
d
P
r
d
1.动手画一个圆,设点到圆心的距离为d,圆的半径为r,量一量在点和圆三种不同位置关系时,d与r有怎样的数量关系?
点在圆外,即d____r.
点在圆上,即d____r.
点在圆内,即d____r.
>
=
<
探究
2.反过来,由d与r的数量关系,怎样判定点和圆的位置关系呢?
d > r,即点在__________.
d = r,即点在__________.
d < r,即点在__________.
圆外
圆上
圆内
r
P
d
P
r
d
P
r
d
点与圆的位置关系有三种:
点在圆外 d>r
点在圆上 d=r
点在圆内 d左端可以推出右端,从右端也可以推出左端
数形结合:
位置关系
数量关系
总结
针对训练
1.已知⊙O的面积为25π.
(1)若PO=5.5,则点P在______;
(2)若PO=4,则点P在______;
(3)若PO=______,则点P在⊙O上.
⊙O外
⊙O内
5
分析:先算半径,再与PO长进行比较.
∵⊙O的面积为25π,
∴⊙O 的半径为5.
1.下列关于圆的说法,正确的是 ( )
A.在平面内圆是所有到定点距离小于等于定长的点的集合
B.同一平面内两个半径相等的圆必定关于某一条直线成轴对称
C.优弧大于劣弧
D.长度一样的弧叫等弧
随堂练习
B
3.已知⊙O的半径为2,AB是⊙O的一条弦,则 AB的长不可能是( )
A. 2 B. 3 C.4 D.5
D
2.已知圆 C 的半径为2,圆心 C 到点 P 的距离为 3,则点 P 与圆C 的位置关系是( )
A.点在圆上 B.点在圆外 C.点在圆内 D.以上都不对
B
4.如图,一根 5m 长的绳子,一端拴在柱子上,另一端栓一只羊 (羊只能在草地上活动),请画出羊的活动区域.
5m
解:如图,以 5m 长为半径作弧,在与墙体相交的部分内,都是羊的活动区域
5.如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,E、F分别是AB、AC的中点.以点B为圆心,BC为半径画圆,判断点A、 C、E、F与⊙B的位置关系,并说明理由.
A
B
C
E
F
解:连接BF. C在⊙B上;在直角△ABC中,
AB=
则A在⊙B的外部;
BE= AB= ×5= <3=BC,则E在⊙B内部;
CP= AC= ×4=2,则在直角△BCF中,
BF= ,则F在⊙B的外部.
试着画出圆的位置!
圆
定义
静态定义:到圆心距离相同的点组成的图形叫圆
动态定义:在一个平面内,线段OA绕一个端点O旋转一周,端点A所经过的路径叫做圆.
弦:直径是圆中最长的弦
弧:劣弧、半圆、优弧.等弧,同弧
有关概念
点在圆外 d>r.
点在圆上 d=r.
点在圆内 d点与圆的
位置关系
课堂小结
3.1 圆
九年级下
北师版
1.经历形成圆概念的过程,经历探索点与圆位置关系的过程.
2.理解圆以及与圆有关的概念,并了解它们之间的区别和联系.
3.初步了解点与圆的位置关系.
学习目标
难点
重点
一些学生正在做投圈游戏,他们的投圈目标都是图中的竹筒,他们呈“一”字排开.
问题:这样的队形对每个人都公平吗?你认为他们应当排成什么样的队形?
新课引入
分析:四位选手分别看作是点A,点B,点C,点D.四个点在同一条直线上,目标看作点O.线段AO,BO,CO,DO长度不都相等.
选手这样站位不公平.
你认为应该怎样站位比较合理?
A
B
C
D
O
A
B
C
D
O
如果每位选手到目标的距离要求是2米,他们可以站在哪些位置?有多少个位置可以选择?
A
B
C
D
O
思考
活动1:平面内有一个定点O,请你画出到点O距离为4cm的点.
问题1:符合条件的点有多少个?
问题2:这些点有什么特征?
新知学习
一 圆的定义
O
1.符合条件的点有无数个
2.圆的静态定义:到定点的距离等于定长的点的集合就是圆.
·
r
O
A
问题3:如图,线段 OA 绕它固定的一个端点 O 旋转一周,另一个端点 A 路径是什么?
2cm
3. 圆的动态定义:在一个平面内,线段 OA 绕一个端点 O 旋转一周,端点 A 所经过的路径叫做圆.其固定的端点 O 叫做圆心,线段 OA 叫做半径. 以点 O为圆心的圆,记作⊙O,读作“圆O”.
想一想,从画圆的过程可以看出什么呢?
(1)圆上各点到定点(圆心O)的距离都等于 .
(2)到定点的距离等于定长的点都在 .
定长r
同一个圆上
圆的集合定义:圆可以看成是平面上到定点的距离等于定长的所有点组成的图形.定点就是圆心,定长就是半径.
1.画一个圆,需要几个要素?
2.圆有什么特征?
思考
确定一个圆需要“两个要素”,一是圆心:圆心定其位置,二是半径:半径定其大小.
圆是一条封闭的曲线,曲线是“圆周”,而不能认为是“圆面”.
问题:现在你能回答本课最开始的问题了吗?
你认为他们应当排成什么样的队形?
为了使游戏公平,这些学生应以竹筒为圆心,以某一名同学到竹筒的距离为半径围成一个圆,因为圆上各点到圆心的距离都等于半径.
针对训练
1.下列关于圆的叙述正确的是( )
A.圆是由圆心唯一确定的
B.圆是一条封闭的曲线
C.到定点的距离小于或等于定长的所有点组成圆
D.圆内任意一点到圆心的距离都相等
B
2.设 AB = 3 cm,画图说明满足:到点 A 和点 B 的距离都小于 2cm 的所有点组成的图形.
解:如图,AB = 3cm,
分别以点 A、点 B 为圆心,2cm 长为半径做圆,
红色部分就是所求图形
A
B
M
N
2.矩形ABCD 的对角线AC,BD相交于点O.求证:A,B,C,D 四个点在以点O为圆心的同一个圆上.
证明:∵四边形ABCD为矩形,
∴OA=OC=AC,OB=OD=BD,AC=BD.
∴OA=OC=OB=OD.
∴A,B,C,D四个点在以点O为圆心,OA为半径的
圆上.
A
B
C
D
O
A,B,C,D四点到圆心O的距离相等
变式:以 AB 为斜边,做一个直角三角形 ABC,求满足条件的所有点 C 组成的图形.
解:以 AB 为斜边,作直角三角形,取AB中点O,
由直角三角形斜边上的中线是斜边的一半可知,
OC = AB,
即OC的长为定值,
∴点C组成的图形为以AB重点O为圆心,OA长为半径的圆.
二 与圆有关的概念
C
A
·
O
B
连接圆上任意两点的线段(如图中的AC)叫做弦.
经过圆心的弦(如图中的AB)叫做直径.
探究
圆中最长的弦是什么?
O
B
O
A
B
O
A
B
O
A
B
C
O
A
B
C
D
O
A
B
C
D
圆中最长的弦是直径.
证明思路:三角形的三边关系可判断.
注意:1.弦和直径都是线段.
2.直径是经过圆心的特殊的弦,是圆中最长的弦,但弦不一定是直径.
·
C
O
A
B
半圆:圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆.
·
C
O
A
B
弧:圆上任意两点间的部分叫做圆弧,简称弧.以A、B为端点的弧记作 AB ,读作“圆弧AB”或“弧AB”.
(
劣弧与优弧:小于半圆的弧叫做劣弧.如图中的AC ;
(
大于半圆的弧叫做优弧.如图中的ABC.
(
能够重合的两个圆叫做等圆.
等圆
半径相同,圆心不同.
同心圆
圆心相同,半径不同。
·
C
O
A
·
C
O1
A
·
C
O
A
长度相等的弧不一定是等弧!
如图,如果AB和CD的拉直长度都是10 cm,平移并调整小圆的位置,是否能使这两条弧完全重合?
D
C
A
B
这两条弧不能完全重合,因为这两条弧半径不同,弧的弯曲程度不同. “等弧”不等于“长度相等的弧”,等弧仅仅存在于同圆或者等圆中.
在同圆或等圆中,能够互相重合的弧叫做等弧.
针对训练
1.以下命题:(1)半圆是弧,但弧不一定是半圆;(2)过圆上任意一点只能作一条弦,且这条弦是直径;(3)弦是直径;(4)直径是圆中最长的弦;(5)直径不是弦;(6)优弧大于劣弧;(7)以O为圆心可以画无数个圆. 正确的个数为( )
A.1 B.2 C.3 D.4
C
观察下图中点和圆的位置关系有哪几种?
.
o
.
.
.
.
.
.
点和圆的位置关系有三种:
点在圆内,点在圆上,点在圆外.
三 点和圆的位置关系
r
P
d
P
r
d
P
r
d
1.动手画一个圆,设点到圆心的距离为d,圆的半径为r,量一量在点和圆三种不同位置关系时,d与r有怎样的数量关系?
点在圆外,即d____r.
点在圆上,即d____r.
点在圆内,即d____r.
>
=
<
探究
2.反过来,由d与r的数量关系,怎样判定点和圆的位置关系呢?
d > r,即点在__________.
d = r,即点在__________.
d < r,即点在__________.
圆外
圆上
圆内
r
P
d
P
r
d
P
r
d
点与圆的位置关系有三种:
点在圆外 d>r
点在圆上 d=r
点在圆内 d
数形结合:
位置关系
数量关系
总结
针对训练
1.已知⊙O的面积为25π.
(1)若PO=5.5,则点P在______;
(2)若PO=4,则点P在______;
(3)若PO=______,则点P在⊙O上.
⊙O外
⊙O内
5
分析:先算半径,再与PO长进行比较.
∵⊙O的面积为25π,
∴⊙O 的半径为5.
1.下列关于圆的说法,正确的是 ( )
A.在平面内圆是所有到定点距离小于等于定长的点的集合
B.同一平面内两个半径相等的圆必定关于某一条直线成轴对称
C.优弧大于劣弧
D.长度一样的弧叫等弧
随堂练习
B
3.已知⊙O的半径为2,AB是⊙O的一条弦,则 AB的长不可能是( )
A. 2 B. 3 C.4 D.5
D
2.已知圆 C 的半径为2,圆心 C 到点 P 的距离为 3,则点 P 与圆C 的位置关系是( )
A.点在圆上 B.点在圆外 C.点在圆内 D.以上都不对
B
4.如图,一根 5m 长的绳子,一端拴在柱子上,另一端栓一只羊 (羊只能在草地上活动),请画出羊的活动区域.
5m
解:如图,以 5m 长为半径作弧,在与墙体相交的部分内,都是羊的活动区域
5.如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,E、F分别是AB、AC的中点.以点B为圆心,BC为半径画圆,判断点A、 C、E、F与⊙B的位置关系,并说明理由.
A
B
C
E
F
解:连接BF. C在⊙B上;在直角△ABC中,
AB=
则A在⊙B的外部;
BE= AB= ×5= <3=BC,则E在⊙B内部;
CP= AC= ×4=2,则在直角△BCF中,
BF= ,则F在⊙B的外部.
试着画出圆的位置!
圆
定义
静态定义:到圆心距离相同的点组成的图形叫圆
动态定义:在一个平面内,线段OA绕一个端点O旋转一周,端点A所经过的路径叫做圆.
弦:直径是圆中最长的弦
弧:劣弧、半圆、优弧.等弧,同弧
有关概念
点在圆外 d>r.
点在圆上 d=r.
点在圆内 d
位置关系
课堂小结
