3.2圆的对称性 课件(共24张PPT)2023-2024学年度北师大版数学九年级下册
文档属性
| 名称 | 3.2圆的对称性 课件(共24张PPT)2023-2024学年度北师大版数学九年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 647.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-17 00:00:00 | ||
图片预览






文档简介
(共24张PPT)
3.2 圆的对称性
九年级下
北师版
1.了解圆的轴对称性及圆的中心对称性及相关性质.
2.掌握圆心角、弧、弦之间关系定理并能利用其解决相关问题.
3.了解圆心角、弧、弦之间关系定理中的“在同圆或等圆”条件的意义.
学习目标
重点
难点
什么是轴对称图形?
什么是中心对称图形?
如果一个图形沿着一条直线对折后两部分能够完全重合,那么这样的图形就叫做轴对称图形
在平面内,把一个图形绕着某个点旋转180°,如果旋转后的图形能与原来的图形完全重合,那么这个图形叫做中心对称图形,这个点叫做它的对称中心。
新课引入
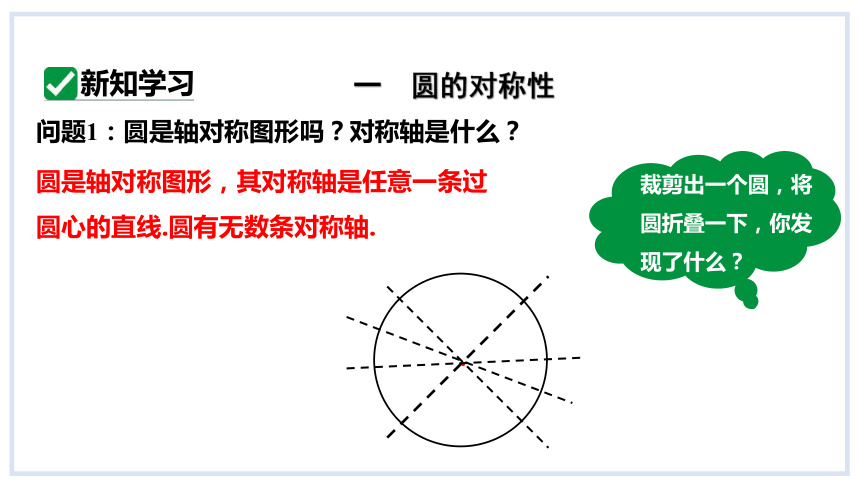
问题1:圆是轴对称图形吗?对称轴是什么?
圆是轴对称图形,其对称轴是任意一条过圆心的直线.圆有无数条对称轴.
一 圆的对称性
新知学习
裁剪出一个圆,将圆折叠一下,你发现了什么?
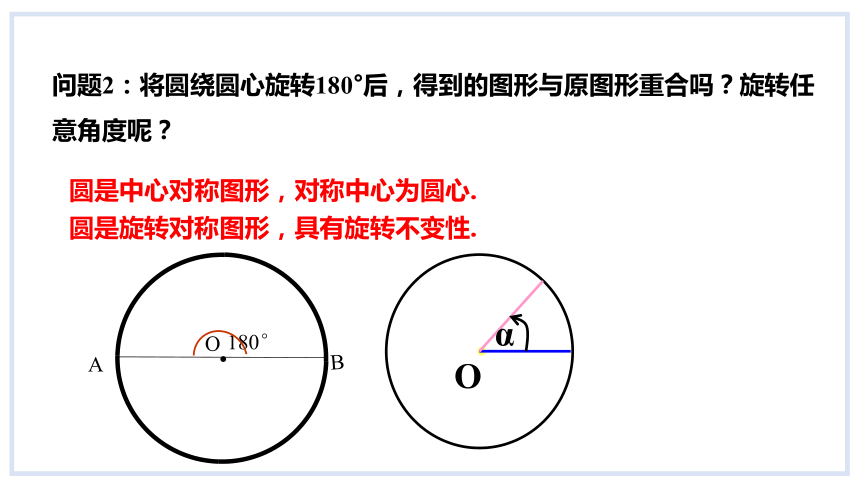
问题2:将圆绕圆心旋转180°后,得到的图形与原图形重合吗?旋转任意角度呢?
圆是中心对称图形,对称中心为圆心.
圆是旋转对称图形,具有旋转不变性.
.
O
A
B
180°
O
α
针对训练
1.日常生活中的许多图案或现象都与圆的对称性有关,试举几例.
碗口,圆桌,圆桌上的转盘,方向盘,圆盘子等
2.下列说法中不正确的是( )
A.经过圆心的直线是圆的对称轴
B.直径是圆的对称轴
C.圆的对称轴有无数条
D.当圆绕它的圆心旋转60°时,仍会与原来的圆重合
B
二 圆心角、弧、弦之间的关系
问题:什么叫圆心角?
顶点在圆心,角的两边与圆相交的角叫圆心角.
右图∠AOB,就是⊙O 的一个圆心角.
A
B
在研究圆心角问题时,常常连接角的两边与圆相交的两点,即连接弦AB,将圆心角放在三角形 ABC 中研究.
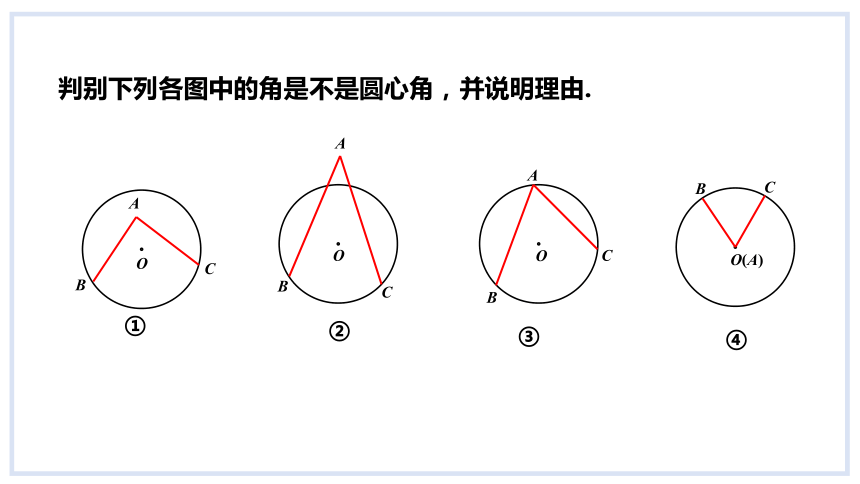
判别下列各图中的角是不是圆心角,并说明理由.
①
②
③
④
A
O
C
B
A
O
C
B
A
O
C
B
O(A)
C
B
在等圆 ⊙O 和⊙O′ 中,分别作相等的圆心角 ∠AOB 和∠A′O′B′,将两圆重叠,并固定圆心,然后把其中的一个圆旋转一个角度,使得 OA 与 O′A′ 重合.
你能发现哪些等量关系?
说一说你的理由.
探究
A
B
O
O′
O(O′)
A′
B′
A′
B′
A
B
小红认为
在等圆中
O′
O(O′)
A′
B′
A′
B′
A
B
在 ⊙O 中作圆心角AOB,得到扇形AOB.
1.把扇形AOB旋转一个角度,得到扇形A′O′B′,圆心角变了吗?弧AB与弧A′B′有什么关系?
探究
在等圆中
圆心角大小不变,弧AB与弧A′B′相等.
2.弦AB与弦A′B′有什么数量关系?
弦AB与弦A′B′相等.
弧、弦与圆心角的关系定理:
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等.
你能归纳一下你发现的等量关系吗
归纳
符号语言:
A
B
A′
B′
O(O′)
∵∠AOB=∠A′OB′
定理“在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等”中,可否把条件“在同圆或等圆中”去掉?为什么?
不可以,如图,如果丢掉了这个前提,即使圆心角相等,所对的弧、弦也不一定相等.
A
B
O
D
C
思考
在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.
归纳
∠AOB=∠A′OB′
A
B
A′
B′
O(O′)
知一推二
例1 如图 ,在⊙O中, ,∠ACB=60°.求证:∠AOB =∠BOC =∠AOC.
O
B
C
A
∴AB =AC.
∴△ABC是等腰三角形.
又∵∠ACB =60°,
∴△ABC是等边三角形,AB=BC=CA,
∴∠AOB =∠BOC =∠AOC.
证明:∵ ,
总结:在同圆或等圆中,两条弧相等,所对的圆心角也相等.
例2 如图, AB,DE是⊙O的直径,C是⊙O上的一点,且 . BE与CE的大小有什么关系?为什么?
·
E
B
C
O
A
D
解:BE=CE. 理由是
∵ ∠AOD=∠BOE,
∴
又∵
∴
∴ BE=CE.
总结:在同圆或等圆中,两条弧相等,所对的两条弦也相等.
(1)如果AB=CD ,那么_________,________________.
(2)如果 ,那么_________,________________.
(3)如果∠AOB=∠COD,
那么_____________,_________.
∠AOB= ∠COD
AB=CD
∠AOB= ∠COD
AB=CD
·
C
A
B
D
O
1.如图,AB、CD是⊙O的两条弦.
针对训练
2.在⊙O中,M,N分别为弦 , 的中点,如果OM=ON,那么在结论:①AB=CD;②AB=CD;③∠AOB=∠COD中,正确的是( )
A.①②
B.①③
C.②③
D.①②③
D
随堂练习
1. 将 按照如图所示的方式分成相等的8个部分,若阴影部分的面积为2,则 的面积为_____.
16
2. 在⊙O中,圆心角∠AOB=2∠COD,则AB与CD的关系是( )
A. AB=2CD
B. AB>2CD
C. AB< 2CD
D.不能确定
C
3.已知A,B是⊙O上的两点,∠AOB = 120°,C是 的中点. 试确定四边形 OACB 的形状,并说明理由.
解:如图,四边形OACB是菱形.理由如下:连接OC.
∵C是 的中点,
∴ ,
∴∠AOC=∠BOC.
∵∠AOB=120°,
∴∠AOC=∠BOC=60°.
4.我们已经知道在⊙O中,如果2∠AOB=∠COD,则 那么CD=2AB也成立吗?若成立,请说明理由;若不成立,那它们之间的关系又是什么?
A
B
C
D
E
O
解:CD=2AB不成立.理由如下:
那么∠AOB=∠COE=∠DOE,
所以弦AB=CE=DE,
在△CDE中,CE+DE>CD,即CD<2AB.
取 的中点E,连接OE,CE,DE.
又∵OB=OC,OA=OC,
∴△BOC 和△AOC都是等边三角形.
∴OB=BC=CA=AO.
∴四边形OACB是菱形.
1. 圆的对称性:
圆是轴对称图形,其对称轴是任意一条过圆心的直线无数条;
圆是中心对称图形,对称中心为圆心.具有旋转不变性.
2. 弧、弦、圆心角之间的关系:
(1)定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等.
(2)推论:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.
课堂小结
3.2 圆的对称性
九年级下
北师版
1.了解圆的轴对称性及圆的中心对称性及相关性质.
2.掌握圆心角、弧、弦之间关系定理并能利用其解决相关问题.
3.了解圆心角、弧、弦之间关系定理中的“在同圆或等圆”条件的意义.
学习目标
重点
难点
什么是轴对称图形?
什么是中心对称图形?
如果一个图形沿着一条直线对折后两部分能够完全重合,那么这样的图形就叫做轴对称图形
在平面内,把一个图形绕着某个点旋转180°,如果旋转后的图形能与原来的图形完全重合,那么这个图形叫做中心对称图形,这个点叫做它的对称中心。
新课引入
问题1:圆是轴对称图形吗?对称轴是什么?
圆是轴对称图形,其对称轴是任意一条过圆心的直线.圆有无数条对称轴.
一 圆的对称性
新知学习
裁剪出一个圆,将圆折叠一下,你发现了什么?
问题2:将圆绕圆心旋转180°后,得到的图形与原图形重合吗?旋转任意角度呢?
圆是中心对称图形,对称中心为圆心.
圆是旋转对称图形,具有旋转不变性.
.
O
A
B
180°
O
α
针对训练
1.日常生活中的许多图案或现象都与圆的对称性有关,试举几例.
碗口,圆桌,圆桌上的转盘,方向盘,圆盘子等
2.下列说法中不正确的是( )
A.经过圆心的直线是圆的对称轴
B.直径是圆的对称轴
C.圆的对称轴有无数条
D.当圆绕它的圆心旋转60°时,仍会与原来的圆重合
B
二 圆心角、弧、弦之间的关系
问题:什么叫圆心角?
顶点在圆心,角的两边与圆相交的角叫圆心角.
右图∠AOB,就是⊙O 的一个圆心角.
A
B
在研究圆心角问题时,常常连接角的两边与圆相交的两点,即连接弦AB,将圆心角放在三角形 ABC 中研究.
判别下列各图中的角是不是圆心角,并说明理由.
①
②
③
④
A
O
C
B
A
O
C
B
A
O
C
B
O(A)
C
B
在等圆 ⊙O 和⊙O′ 中,分别作相等的圆心角 ∠AOB 和∠A′O′B′,将两圆重叠,并固定圆心,然后把其中的一个圆旋转一个角度,使得 OA 与 O′A′ 重合.
你能发现哪些等量关系?
说一说你的理由.
探究
A
B
O
O′
O(O′)
A′
B′
A′
B′
A
B
小红认为
在等圆中
O′
O(O′)
A′
B′
A′
B′
A
B
在 ⊙O 中作圆心角AOB,得到扇形AOB.
1.把扇形AOB旋转一个角度,得到扇形A′O′B′,圆心角变了吗?弧AB与弧A′B′有什么关系?
探究
在等圆中
圆心角大小不变,弧AB与弧A′B′相等.
2.弦AB与弦A′B′有什么数量关系?
弦AB与弦A′B′相等.
弧、弦与圆心角的关系定理:
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等.
你能归纳一下你发现的等量关系吗
归纳
符号语言:
A
B
A′
B′
O(O′)
∵∠AOB=∠A′OB′
定理“在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等”中,可否把条件“在同圆或等圆中”去掉?为什么?
不可以,如图,如果丢掉了这个前提,即使圆心角相等,所对的弧、弦也不一定相等.
A
B
O
D
C
思考
在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.
归纳
∠AOB=∠A′OB′
A
B
A′
B′
O(O′)
知一推二
例1 如图 ,在⊙O中, ,∠ACB=60°.求证:∠AOB =∠BOC =∠AOC.
O
B
C
A
∴AB =AC.
∴△ABC是等腰三角形.
又∵∠ACB =60°,
∴△ABC是等边三角形,AB=BC=CA,
∴∠AOB =∠BOC =∠AOC.
证明:∵ ,
总结:在同圆或等圆中,两条弧相等,所对的圆心角也相等.
例2 如图, AB,DE是⊙O的直径,C是⊙O上的一点,且 . BE与CE的大小有什么关系?为什么?
·
E
B
C
O
A
D
解:BE=CE. 理由是
∵ ∠AOD=∠BOE,
∴
又∵
∴
∴ BE=CE.
总结:在同圆或等圆中,两条弧相等,所对的两条弦也相等.
(1)如果AB=CD ,那么_________,________________.
(2)如果 ,那么_________,________________.
(3)如果∠AOB=∠COD,
那么_____________,_________.
∠AOB= ∠COD
AB=CD
∠AOB= ∠COD
AB=CD
·
C
A
B
D
O
1.如图,AB、CD是⊙O的两条弦.
针对训练
2.在⊙O中,M,N分别为弦 , 的中点,如果OM=ON,那么在结论:①AB=CD;②AB=CD;③∠AOB=∠COD中,正确的是( )
A.①②
B.①③
C.②③
D.①②③
D
随堂练习
1. 将 按照如图所示的方式分成相等的8个部分,若阴影部分的面积为2,则 的面积为_____.
16
2. 在⊙O中,圆心角∠AOB=2∠COD,则AB与CD的关系是( )
A. AB=2CD
B. AB>2CD
C. AB< 2CD
D.不能确定
C
3.已知A,B是⊙O上的两点,∠AOB = 120°,C是 的中点. 试确定四边形 OACB 的形状,并说明理由.
解:如图,四边形OACB是菱形.理由如下:连接OC.
∵C是 的中点,
∴ ,
∴∠AOC=∠BOC.
∵∠AOB=120°,
∴∠AOC=∠BOC=60°.
4.我们已经知道在⊙O中,如果2∠AOB=∠COD,则 那么CD=2AB也成立吗?若成立,请说明理由;若不成立,那它们之间的关系又是什么?
A
B
C
D
E
O
解:CD=2AB不成立.理由如下:
那么∠AOB=∠COE=∠DOE,
所以弦AB=CE=DE,
在△CDE中,CE+DE>CD,即CD<2AB.
取 的中点E,连接OE,CE,DE.
又∵OB=OC,OA=OC,
∴△BOC 和△AOC都是等边三角形.
∴OB=BC=CA=AO.
∴四边形OACB是菱形.
1. 圆的对称性:
圆是轴对称图形,其对称轴是任意一条过圆心的直线无数条;
圆是中心对称图形,对称中心为圆心.具有旋转不变性.
2. 弧、弦、圆心角之间的关系:
(1)定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等.
(2)推论:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.
课堂小结
