3.7切线长定理 课件(共22张PPT)2023-2024学年度北师大版数学九年级下册
文档属性
| 名称 | 3.7切线长定理 课件(共22张PPT)2023-2024学年度北师大版数学九年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 237.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-17 13:24:22 | ||
图片预览








文档简介
(共22张PPT)
3.7 切线长定理
九年级下
北师版
1.证明并探索切线长定理.
2.初步学会运用切线长定理进行计算与证明.
学习目标
重点
难点
前面我们已经学习了切线的判定和性质,现知⊙O和⊙O外一点P.
1.你能够过点P画出⊙O的切线吗?
2.将这个图形沿着OP折叠,你能发现哪些边和角的数量关系?
新课引入
一 切线长的定义
切线长的定义:
经过圆外一点作圆的切线,这点和切点之间的线段的长叫作切线长.
思考
切线长和切线的区别和联系?
P
O
A
B
新知学习
1.切线是直线,不能度量.
2.切线长是线段的长,这条线段的两个端点分别是圆外一点和切点,可以度量.
如图,PA、PB 是⊙O的两条切线,A,B 是切点.
(1)这个图形是轴对称图形吗?如果是,它的对称轴是什么?
是轴对称图形,对称轴是直线 OP .
二 切线长定理
O
P
A
B
(2)图中的PA与PB,∠APO=∠BPO有什么关系?
PA=PB,∠APO=∠BPO
探究
如图,连接OA和OB.
∵PA和PB是⊙O的两条切线,
∴OA⊥AP,OB⊥BP.
又OA=OB,OP=OP.
∴Rt△AOP ≌ Rt△BOP.
∴PA=PB,∠APO=∠BPO.
P
O
A
B
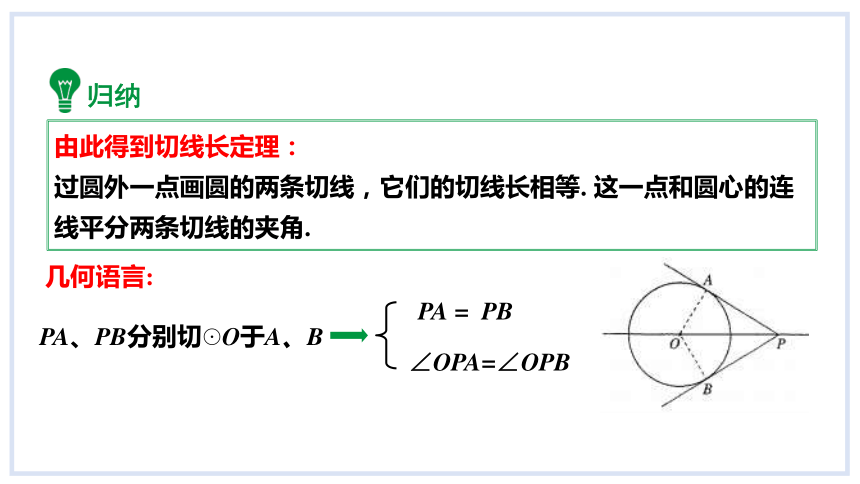
由此得到切线长定理:
过圆外一点画圆的两条切线,它们的切线长相等. 这一点和圆心的连线平分两条切线的夹角.
PA、PB分别切☉O于A、B
PA = PB
∠OPA=∠OPB
几何语言:
归纳
例1 观察五粮液酒厂东大门的标志,我们从中得到了下图所示的数学图形,已知 AP,BP 分别与 ⊙O 相切与A、B两点,切线长 AP = 1m,点 O 到点 P 的距离是 2m.
(1) BP = ________;
(2) ⊙O的半径 r = __________;
(3) 连接 OP,则∠OPA = __________°;
(4) ∠APB = __________°;
(5) 连接 AB,AB = __________.
O
A
B
P
1m
60
120
m
m
如图,四边形 ABCD 的四条边都与⊙O 相切,图中的线段之间有哪些等量关系?
A
B
O
C
D
E
F
G
H
结论:圆的外切四边形的两组对边的和相等.
即 AD+BC=AB+CD.
探究
例2 PA、PB是☉O的两条切线,A、B为切点,直线OP交☉O于点D、E,交AB于C.
B
P
O
A
C
E
D
(1)写出图中所有的垂直关系;
OA⊥PA,OB ⊥PB,AB ⊥OP.
(2)写出图中与∠OAC相等的角;
∠OAC=∠OBC=∠APC=∠BPC.
(3)写出图中所有的全等三角形;
△AOP≌△BOP, △AOC≌△BOC, △ACP≌△BCP.
(4)写出图中所有的等腰三角形.
△ABP 、△AOB
B
P
O
A
C
E
D
例3 如图,在Rt△ABC 中, ∠C=90°,AC=10,BC=24,⊙O 是△ABC 的内切圆,切点分别为 D,E,F,求⊙O 的半径.
解:连接OD,OE,OF,
则OD=OE=OF,
设OD=r.
在△ABC中,AC=10, BC=24,
∴AB = = 26.
分析:关键是熟练运用切线长定理,将相等线段转化集中到某条边上,从而建立方程.
∵⊙O分别与AB,BC, AC相切于点D,E,F,
∴OD⊥AB,OE ⊥ BC, OF ⊥ AC,BD = BE,AD = AF,CE=CF.
又∵ ∠ C=90°,
∴四边形OECF为正方形.
∴ CE=CF=r.
∴ BE = 24-r, AF=10-r.
∴ AB = BD + AD = BE+AF =24-r+ 10-r= 34-2r.
而AB = 26, ∴ 34 -2r = 26.
∴ r = 4, 即 ⊙O 的半径为4.
归纳
(3)连接圆心和圆外一点.
(2)连接两切点;
(1)分别连接圆心和切点;
切线长问题辅助线添加方法
1.下列说法正确的是( )
A.过任意一点总可以作圆的两条切线
B.圆的切线长就是圆的切线的长度
C.过圆外一点所画的圆的两条切线长相等
D.过圆外一点所画的圆的切线长一定大于圆的半径
C
针对训练
B
P
O
A
2.PA、PB是☉O的两条切线,A,B是切点,OA=3.
(1)若AP=4,则OP= ;
(2)若∠BPA=60 °,则OP= .
5
6
3.△ABC 的内切圆⊙O与BC、CA、AB分别相切于点D、E、F,且
AB=13cm,BC=14cm,CA=9cm,求AF、BD、CE的长.
解:
设AF=xcm,则AE=xcm.
∴CE=CD=AC-AE=(9-x)cm,
BF=BD=AB-AF=(13-x)cm.
A
C
B
E
D
F
O
由 BD+CD=BC,可得
(13-x)+(9-x)=14,
∴ AF=4cm,BD=9cm,CE=5cm.
解得 x=4.
A
C
B
E
D
F
O
随堂练习
1.如图,四边形ABCD为正方形,边长为4,点E是BC边上一点,以AB为直径的半圆切DE于点F,则BE的长为_______
2.如图,四边形ABCD为☉O的内接四边形,过点A,B的切线PM,PN交于圆外一点P,若∠C=135°,∠MAD=60°,则P的度数为_______
P
A
B
C
D
O
30°
辅助线
概念
切线长定理
过圆外一点画圆的两条切线,它们的切线长相等. 这一点和圆心的连线平分两条切线的夹角.
3.连接圆心和圆外一点.
2.连接两切点;
1.分别连接圆心和切点;
课堂小结
3.7 切线长定理
九年级下
北师版
1.证明并探索切线长定理.
2.初步学会运用切线长定理进行计算与证明.
学习目标
重点
难点
前面我们已经学习了切线的判定和性质,现知⊙O和⊙O外一点P.
1.你能够过点P画出⊙O的切线吗?
2.将这个图形沿着OP折叠,你能发现哪些边和角的数量关系?
新课引入
一 切线长的定义
切线长的定义:
经过圆外一点作圆的切线,这点和切点之间的线段的长叫作切线长.
思考
切线长和切线的区别和联系?
P
O
A
B
新知学习
1.切线是直线,不能度量.
2.切线长是线段的长,这条线段的两个端点分别是圆外一点和切点,可以度量.
如图,PA、PB 是⊙O的两条切线,A,B 是切点.
(1)这个图形是轴对称图形吗?如果是,它的对称轴是什么?
是轴对称图形,对称轴是直线 OP .
二 切线长定理
O
P
A
B
(2)图中的PA与PB,∠APO=∠BPO有什么关系?
PA=PB,∠APO=∠BPO
探究
如图,连接OA和OB.
∵PA和PB是⊙O的两条切线,
∴OA⊥AP,OB⊥BP.
又OA=OB,OP=OP.
∴Rt△AOP ≌ Rt△BOP.
∴PA=PB,∠APO=∠BPO.
P
O
A
B
由此得到切线长定理:
过圆外一点画圆的两条切线,它们的切线长相等. 这一点和圆心的连线平分两条切线的夹角.
PA、PB分别切☉O于A、B
PA = PB
∠OPA=∠OPB
几何语言:
归纳
例1 观察五粮液酒厂东大门的标志,我们从中得到了下图所示的数学图形,已知 AP,BP 分别与 ⊙O 相切与A、B两点,切线长 AP = 1m,点 O 到点 P 的距离是 2m.
(1) BP = ________;
(2) ⊙O的半径 r = __________;
(3) 连接 OP,则∠OPA = __________°;
(4) ∠APB = __________°;
(5) 连接 AB,AB = __________.
O
A
B
P
1m
60
120
m
m
如图,四边形 ABCD 的四条边都与⊙O 相切,图中的线段之间有哪些等量关系?
A
B
O
C
D
E
F
G
H
结论:圆的外切四边形的两组对边的和相等.
即 AD+BC=AB+CD.
探究
例2 PA、PB是☉O的两条切线,A、B为切点,直线OP交☉O于点D、E,交AB于C.
B
P
O
A
C
E
D
(1)写出图中所有的垂直关系;
OA⊥PA,OB ⊥PB,AB ⊥OP.
(2)写出图中与∠OAC相等的角;
∠OAC=∠OBC=∠APC=∠BPC.
(3)写出图中所有的全等三角形;
△AOP≌△BOP, △AOC≌△BOC, △ACP≌△BCP.
(4)写出图中所有的等腰三角形.
△ABP 、△AOB
B
P
O
A
C
E
D
例3 如图,在Rt△ABC 中, ∠C=90°,AC=10,BC=24,⊙O 是△ABC 的内切圆,切点分别为 D,E,F,求⊙O 的半径.
解:连接OD,OE,OF,
则OD=OE=OF,
设OD=r.
在△ABC中,AC=10, BC=24,
∴AB = = 26.
分析:关键是熟练运用切线长定理,将相等线段转化集中到某条边上,从而建立方程.
∵⊙O分别与AB,BC, AC相切于点D,E,F,
∴OD⊥AB,OE ⊥ BC, OF ⊥ AC,BD = BE,AD = AF,CE=CF.
又∵ ∠ C=90°,
∴四边形OECF为正方形.
∴ CE=CF=r.
∴ BE = 24-r, AF=10-r.
∴ AB = BD + AD = BE+AF =24-r+ 10-r= 34-2r.
而AB = 26, ∴ 34 -2r = 26.
∴ r = 4, 即 ⊙O 的半径为4.
归纳
(3)连接圆心和圆外一点.
(2)连接两切点;
(1)分别连接圆心和切点;
切线长问题辅助线添加方法
1.下列说法正确的是( )
A.过任意一点总可以作圆的两条切线
B.圆的切线长就是圆的切线的长度
C.过圆外一点所画的圆的两条切线长相等
D.过圆外一点所画的圆的切线长一定大于圆的半径
C
针对训练
B
P
O
A
2.PA、PB是☉O的两条切线,A,B是切点,OA=3.
(1)若AP=4,则OP= ;
(2)若∠BPA=60 °,则OP= .
5
6
3.△ABC 的内切圆⊙O与BC、CA、AB分别相切于点D、E、F,且
AB=13cm,BC=14cm,CA=9cm,求AF、BD、CE的长.
解:
设AF=xcm,则AE=xcm.
∴CE=CD=AC-AE=(9-x)cm,
BF=BD=AB-AF=(13-x)cm.
A
C
B
E
D
F
O
由 BD+CD=BC,可得
(13-x)+(9-x)=14,
∴ AF=4cm,BD=9cm,CE=5cm.
解得 x=4.
A
C
B
E
D
F
O
随堂练习
1.如图,四边形ABCD为正方形,边长为4,点E是BC边上一点,以AB为直径的半圆切DE于点F,则BE的长为_______
2.如图,四边形ABCD为☉O的内接四边形,过点A,B的切线PM,PN交于圆外一点P,若∠C=135°,∠MAD=60°,则P的度数为_______
P
A
B
C
D
O
30°
辅助线
概念
切线长定理
过圆外一点画圆的两条切线,它们的切线长相等. 这一点和圆心的连线平分两条切线的夹角.
3.连接圆心和圆外一点.
2.连接两切点;
1.分别连接圆心和切点;
课堂小结
