3.9弧长及扇形的面积 课件(共35张PPT)2023-2024学年度北师大版数学九年级下册
文档属性
| 名称 | 3.9弧长及扇形的面积 课件(共35张PPT)2023-2024学年度北师大版数学九年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 784.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-17 13:38:24 | ||
图片预览








文档简介
(共35张PPT)
3.9 弧长及扇形面积
九年级下
北师版
1.经历探索弧长计算公式和扇形面积计算公式的过程.
2.会运用弧长计算公式和扇形面积的计算公式进行计算.
学习目标
重点
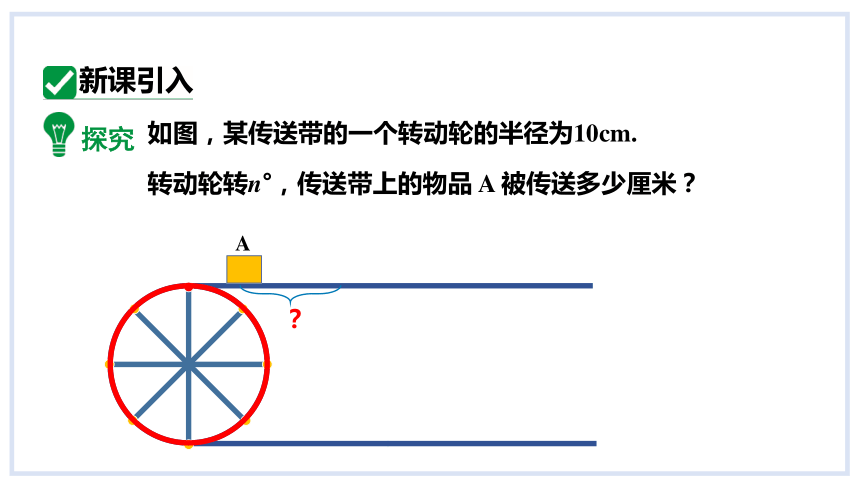
探究
A
?
如图,某传送带的一个转动轮的半径为10cm.
转动轮转n°,传送带上的物品 A 被传送多少厘米?
新课引入
问题1 半径为r的圆,周长是多少?面积是多少?
问题2 什么是弧长?
问题3 弧长和哪些量有关?
半径和圆心角
弧长是弧的长度
S=πr2
知识回顾
O
A
B
n°
r
c
(1) 圆心角是180°,占整个周角的 ,因此它所对的弧长是圆周长的______.
(2) 圆心角是90°,占整个周角的 ,因此它所对的弧长是圆周长的______.
O
R
180°
O
R
90°
问题4 下图中各圆心角所对的弧长分别是圆周长的几分之几
(3) 圆心角是45°,占整个周角的 ,因此它所对的弧长是圆周长的_______.
(4) 圆心角是n°,占整个周角的 ,因此它所对的弧长是圆周长的_______.
O
R
45°
O
R
n°
一 与弧长相关的计算
探究
新知学习
A
2πr
=20πcm
如图,某传送带的一个转动轮的半径为10cm.
(1)转动轮转一周,传送带上的物品 A 被传送多少厘米?
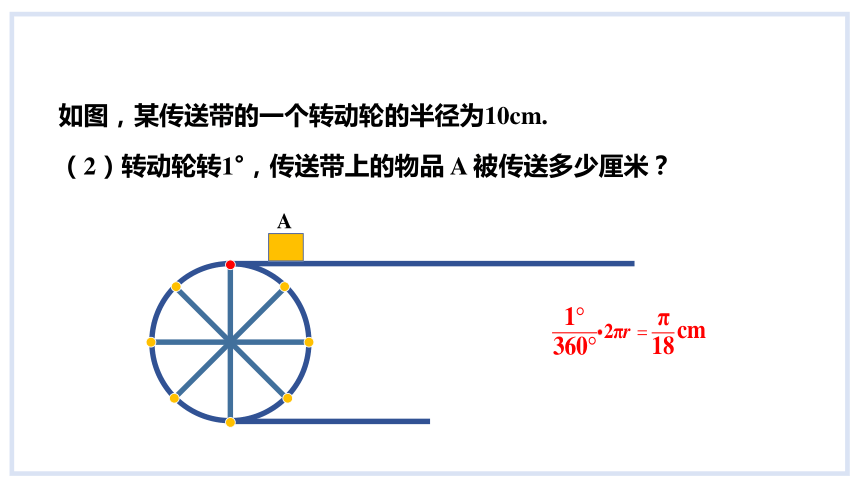
如图,某传送带的一个转动轮的半径为10cm.
(2)转动轮转1°,传送带上的物品 A 被传送多少厘米?
A
如图,某传送带的一个转动轮的半径为10cm.
(3)转动轮转n°,传送带上的物品 A 被传送多少厘米?
A
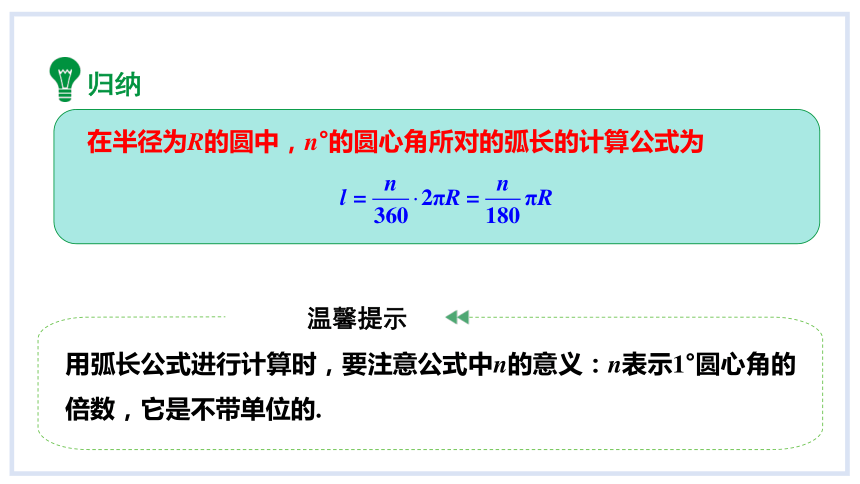
归纳
用弧长公式进行计算时,要注意公式中n的意义:n表示1°圆心角的倍数,它是不带单位的.
温馨提示
在半径为R的圆中,n°的圆心角所对的弧长的计算公式为
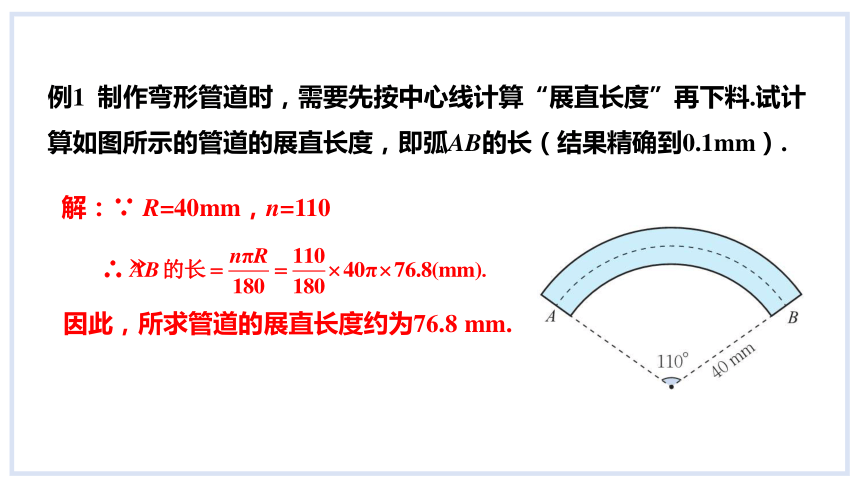
例1 制作弯形管道时,需要先按中心线计算“展直长度”再下料.试计算如图所示的管道的展直长度,即弧AB的长(结果精确到0.1mm).
因此,所求管道的展直长度约为76.8 mm.
解:∵ R=40mm,n=110
∴
针对训练
1.在半径为6的⊙O中,60°圆心角所对的弧长( )
A.π
B.2π
C.4π
D.6π
B
2.如图,是一个圆形人工湖,弦AB是湖上的一座桥.已知AB的长为10,圆周角∠C=30°,则弧AB的长为( )
A. π
B. π
C. π
D. π
B
在一块空旷的草地上有一根柱子,柱子上拴着一条长3 m 的绳子,绳子的一端拴着一只狗.
(1)这只狗的最大活动区域有多大?
解:由题意得,这只狗的最大活动区域为
二 与扇形面积相关的计算
(2)如果这只狗拴在夹角为n°的墙角 ,那么它的最大活动区域有多大?
狗活动的区域是一个什么图形呢?如何求它的面积?
n°
3m
圆的一条弧和经过这条弧的端点的两条半径所围成的图形叫做扇形.
半径
半径
O
B
A
圆心角
弧
O
B
A
扇形
如图,绿色部分是一个扇形,记作扇形OAB.
探究
问题1 半径为r的圆,面积是多少?
O
r
问题2 下图中各扇形面积分别是圆面积的几分之几,具体是多少呢
O
r
90°
圆心角占
周角的比例 扇形面积占
圆面积的比例 扇形的
面积
=
O
r
180°
O
r
45°
O
r
n°
=
=
=
扇形面积公式
半径为r的圆中,圆心角为n°的扇形的面积
①公式中n的意义:n表示1°圆心角的倍数,它是不带单位的;
②公式要理解记忆(即按照上面推导过程记忆).
归纳
思考
扇形的弧长公式与面积公式有联系吗?
A
B
O
O
例2 扇形AOB的半径为12 cm, ∠ AOB=120°,求 的长(结果精确到 0.1 cm)和扇形AOB的面积(结果精确到0.1 cm2).
解: 的长 25.1 ( cm).
S扇形 150.7 (cm2 ).
因此, 的长约为25.1 cm,扇形AOB的面积约为150.7 cm2.
例3 如图,水平放置的圆柱形排水管道的截面半径是0.6 m,其中水面高 0.3 m,求截面上有水部分的面积(结果保留小数点后两位).
O
解:如解图,连接OA,OB,作弦AB的垂直平分线,垂足为D,交AB于点C,连接AC.
∵OC=0.6 m,DC=0.3 m,
∴OD=OC-DC=0.3(m).
∴OD=DC.
又AD⊥DC,
∴AD是线段OC的垂直平分线.
∴AC=AO=OC.
O
A
B
C
D
从而∠AOD=60°,∠AOB=120°.
有水部分的面积
O
A
B
C
D
O
O
弓形的面积=扇形的面积±三角形的面积
S弓形=S扇形-S三角形
S弓形=S扇形+S三角形
弓形的面积公式
归纳
针对训练
1.某扇形的圆心角为72°,面积为5π,则此扇形的弧长为( )
A.π
B.2π
C.3π
D.4π
B
2.如图所示,已知扇形AOB 的半径为2,圆心角为90°,连接AB,则图中阴影部分的面积是( )
A. π-2
B. π-4
C. 4π-2
D.4π-4
A
3.如图,∠ACB是⊙O的圆周角,若⊙O的半径为10,∠ACB=45°,则扇形AOB的面积为( )
A.5π
B.12.5π
C.20π
D.25π
D
随堂练习
1.(2023浙江丽水)某仿古墙上原有一个矩形的门洞,现要将它改为一个圆弧形的门洞,圆弧所在的圆外接于矩形,如图.已知矩形的宽为2 m,高为2m,则改建后门洞的圆弧长是( )
C
A. m B. m
C. m D. m
2.(2023山东泰安)如图,四边形ABCD中,∠A=60°,AB∥CD,DE⊥AD交AB于点E,以点E为圆心,DE为半径,且DE=6的圆交CD于点F,则阴影部分的面积为( )
A. 6π-9
B. 12π-9
C. 6π-
D. 12π-
B
3.(2022黑龙江齐齐哈尔)如图,在△ABC中,AB=AC,以AB为直径作⊙O,AC与⊙O交于点D,BC与⊙O交于点E,过点C作CF∥AB,且 CF=CD,连接BF.
(1)求证:BF是⊙O的切线;
(1)证明:如图,连接BD,
∵AB是⊙O的直径,∴∠BDA=90°,∴∠BDC=90°,
∵AB=AC,∴∠ABC=∠ACB.
∵CF∥AB,
∴∠FCB=∠ABC,∠ABF+∠F=180°,∴∠FCB=∠ACB,
∵CF=CD,BC=BC,
∴△BCF≌△BCD.
∴∠F=∠BDC=90°,
又∵∠ABF+∠F=180°,
∴∠ABF=90°,且AB是⊙O的直径,
∴BF是⊙O的切线;
(2)若∠BAC=45°,AD=4,求图中阴影部分的面积
(2)解:如解图,连接OE,与BD交于点M,
∵∠BDA=90°,∠BAC=45°,AD=4,∴BD=AD=4,∴AB=
∴OB=
∴OE=OB=
∴∠OEB=∠ABC.
∵AB=AC,∠BAC=45°,
∴∠BOE=∠BAC=45°,
∴OE∥AC.
∴∠OMB=∠ADB=90°,
∴BM=OM=2.
∴S阴影=S扇形BOE-S△OBE=
扇形面积
弧长
计算公式:
弧长和
扇形面积
计算公式:
弓形面积
计算公式:
S弓形=S扇形-S三角形
S弓形=S扇形+S三角形
割补法
课堂小结
3.9 弧长及扇形面积
九年级下
北师版
1.经历探索弧长计算公式和扇形面积计算公式的过程.
2.会运用弧长计算公式和扇形面积的计算公式进行计算.
学习目标
重点
探究
A
?
如图,某传送带的一个转动轮的半径为10cm.
转动轮转n°,传送带上的物品 A 被传送多少厘米?
新课引入
问题1 半径为r的圆,周长是多少?面积是多少?
问题2 什么是弧长?
问题3 弧长和哪些量有关?
半径和圆心角
弧长是弧的长度
S=πr2
知识回顾
O
A
B
n°
r
c
(1) 圆心角是180°,占整个周角的 ,因此它所对的弧长是圆周长的______.
(2) 圆心角是90°,占整个周角的 ,因此它所对的弧长是圆周长的______.
O
R
180°
O
R
90°
问题4 下图中各圆心角所对的弧长分别是圆周长的几分之几
(3) 圆心角是45°,占整个周角的 ,因此它所对的弧长是圆周长的_______.
(4) 圆心角是n°,占整个周角的 ,因此它所对的弧长是圆周长的_______.
O
R
45°
O
R
n°
一 与弧长相关的计算
探究
新知学习
A
2πr
=20πcm
如图,某传送带的一个转动轮的半径为10cm.
(1)转动轮转一周,传送带上的物品 A 被传送多少厘米?
如图,某传送带的一个转动轮的半径为10cm.
(2)转动轮转1°,传送带上的物品 A 被传送多少厘米?
A
如图,某传送带的一个转动轮的半径为10cm.
(3)转动轮转n°,传送带上的物品 A 被传送多少厘米?
A
归纳
用弧长公式进行计算时,要注意公式中n的意义:n表示1°圆心角的倍数,它是不带单位的.
温馨提示
在半径为R的圆中,n°的圆心角所对的弧长的计算公式为
例1 制作弯形管道时,需要先按中心线计算“展直长度”再下料.试计算如图所示的管道的展直长度,即弧AB的长(结果精确到0.1mm).
因此,所求管道的展直长度约为76.8 mm.
解:∵ R=40mm,n=110
∴
针对训练
1.在半径为6的⊙O中,60°圆心角所对的弧长( )
A.π
B.2π
C.4π
D.6π
B
2.如图,是一个圆形人工湖,弦AB是湖上的一座桥.已知AB的长为10,圆周角∠C=30°,则弧AB的长为( )
A. π
B. π
C. π
D. π
B
在一块空旷的草地上有一根柱子,柱子上拴着一条长3 m 的绳子,绳子的一端拴着一只狗.
(1)这只狗的最大活动区域有多大?
解:由题意得,这只狗的最大活动区域为
二 与扇形面积相关的计算
(2)如果这只狗拴在夹角为n°的墙角 ,那么它的最大活动区域有多大?
狗活动的区域是一个什么图形呢?如何求它的面积?
n°
3m
圆的一条弧和经过这条弧的端点的两条半径所围成的图形叫做扇形.
半径
半径
O
B
A
圆心角
弧
O
B
A
扇形
如图,绿色部分是一个扇形,记作扇形OAB.
探究
问题1 半径为r的圆,面积是多少?
O
r
问题2 下图中各扇形面积分别是圆面积的几分之几,具体是多少呢
O
r
90°
圆心角占
周角的比例 扇形面积占
圆面积的比例 扇形的
面积
=
O
r
180°
O
r
45°
O
r
n°
=
=
=
扇形面积公式
半径为r的圆中,圆心角为n°的扇形的面积
①公式中n的意义:n表示1°圆心角的倍数,它是不带单位的;
②公式要理解记忆(即按照上面推导过程记忆).
归纳
思考
扇形的弧长公式与面积公式有联系吗?
A
B
O
O
例2 扇形AOB的半径为12 cm, ∠ AOB=120°,求 的长(结果精确到 0.1 cm)和扇形AOB的面积(结果精确到0.1 cm2).
解: 的长 25.1 ( cm).
S扇形 150.7 (cm2 ).
因此, 的长约为25.1 cm,扇形AOB的面积约为150.7 cm2.
例3 如图,水平放置的圆柱形排水管道的截面半径是0.6 m,其中水面高 0.3 m,求截面上有水部分的面积(结果保留小数点后两位).
O
解:如解图,连接OA,OB,作弦AB的垂直平分线,垂足为D,交AB于点C,连接AC.
∵OC=0.6 m,DC=0.3 m,
∴OD=OC-DC=0.3(m).
∴OD=DC.
又AD⊥DC,
∴AD是线段OC的垂直平分线.
∴AC=AO=OC.
O
A
B
C
D
从而∠AOD=60°,∠AOB=120°.
有水部分的面积
O
A
B
C
D
O
O
弓形的面积=扇形的面积±三角形的面积
S弓形=S扇形-S三角形
S弓形=S扇形+S三角形
弓形的面积公式
归纳
针对训练
1.某扇形的圆心角为72°,面积为5π,则此扇形的弧长为( )
A.π
B.2π
C.3π
D.4π
B
2.如图所示,已知扇形AOB 的半径为2,圆心角为90°,连接AB,则图中阴影部分的面积是( )
A. π-2
B. π-4
C. 4π-2
D.4π-4
A
3.如图,∠ACB是⊙O的圆周角,若⊙O的半径为10,∠ACB=45°,则扇形AOB的面积为( )
A.5π
B.12.5π
C.20π
D.25π
D
随堂练习
1.(2023浙江丽水)某仿古墙上原有一个矩形的门洞,现要将它改为一个圆弧形的门洞,圆弧所在的圆外接于矩形,如图.已知矩形的宽为2 m,高为2m,则改建后门洞的圆弧长是( )
C
A. m B. m
C. m D. m
2.(2023山东泰安)如图,四边形ABCD中,∠A=60°,AB∥CD,DE⊥AD交AB于点E,以点E为圆心,DE为半径,且DE=6的圆交CD于点F,则阴影部分的面积为( )
A. 6π-9
B. 12π-9
C. 6π-
D. 12π-
B
3.(2022黑龙江齐齐哈尔)如图,在△ABC中,AB=AC,以AB为直径作⊙O,AC与⊙O交于点D,BC与⊙O交于点E,过点C作CF∥AB,且 CF=CD,连接BF.
(1)求证:BF是⊙O的切线;
(1)证明:如图,连接BD,
∵AB是⊙O的直径,∴∠BDA=90°,∴∠BDC=90°,
∵AB=AC,∴∠ABC=∠ACB.
∵CF∥AB,
∴∠FCB=∠ABC,∠ABF+∠F=180°,∴∠FCB=∠ACB,
∵CF=CD,BC=BC,
∴△BCF≌△BCD.
∴∠F=∠BDC=90°,
又∵∠ABF+∠F=180°,
∴∠ABF=90°,且AB是⊙O的直径,
∴BF是⊙O的切线;
(2)若∠BAC=45°,AD=4,求图中阴影部分的面积
(2)解:如解图,连接OE,与BD交于点M,
∵∠BDA=90°,∠BAC=45°,AD=4,∴BD=AD=4,∴AB=
∴OB=
∴OE=OB=
∴∠OEB=∠ABC.
∵AB=AC,∠BAC=45°,
∴∠BOE=∠BAC=45°,
∴OE∥AC.
∴∠OMB=∠ADB=90°,
∴BM=OM=2.
∴S阴影=S扇形BOE-S△OBE=
扇形面积
弧长
计算公式:
弧长和
扇形面积
计算公式:
弓形面积
计算公式:
S弓形=S扇形-S三角形
S弓形=S扇形+S三角形
割补法
课堂小结
