2024年中考 数学专题提升04 分 式(含答案)
文档属性
| 名称 | 2024年中考 数学专题提升04 分 式(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 184.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-17 19:18:58 | ||
图片预览
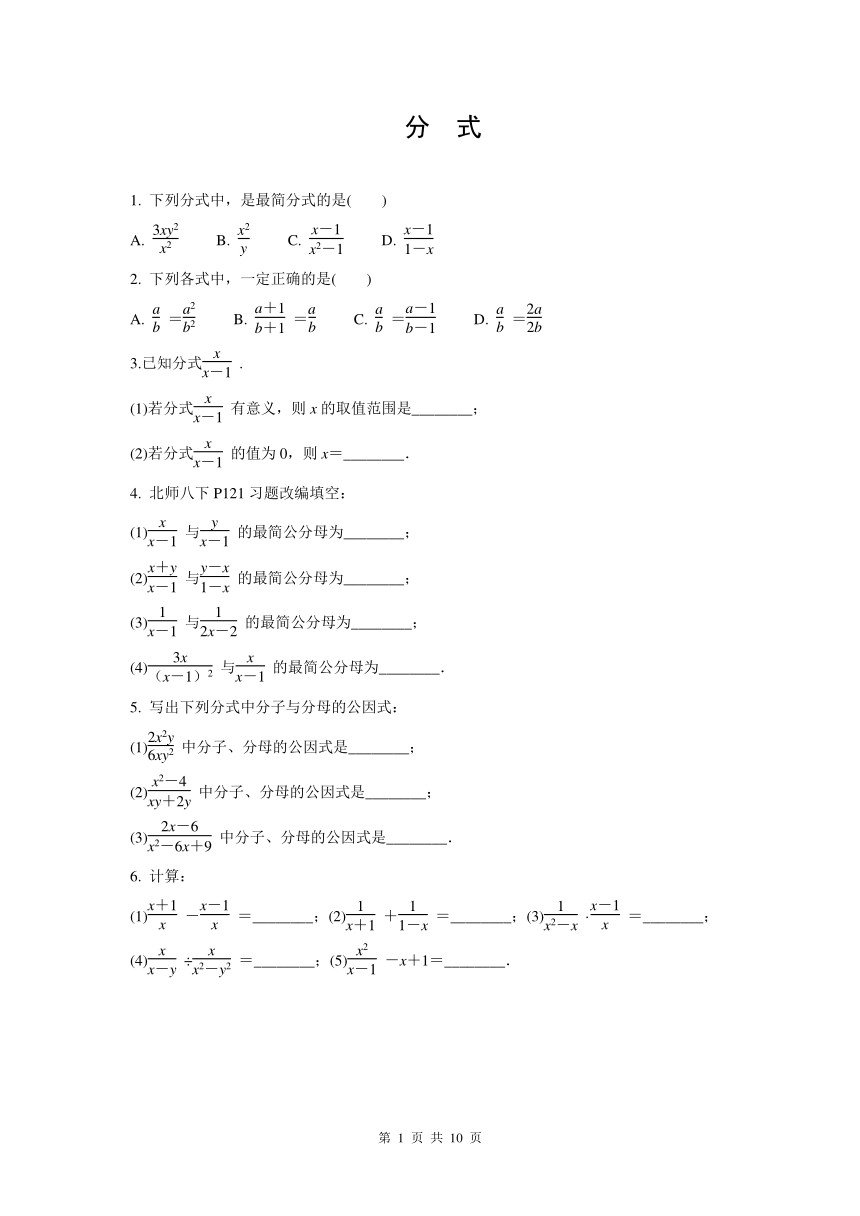




文档简介
分 式
1. 下列分式中,是最简分式的是( )
A. B. C. D.
2. 下列各式中,一定正确的是( )
A. = B. = C. = D. =
3.已知分式.
(1)若分式有意义,则x的取值范围是________;
(2)若分式的值为0,则x=________.
4. 北师八下P121习题改编填空:
(1)与的最简公分母为________;
(2)与的最简公分母为________;
(3)与的最简公分母为________;
(4)与的最简公分母为________.
5. 写出下列分式中分子与分母的公因式:
(1)中分子、分母的公因式是________;
(2)中分子、分母的公因式是________;
(3)中分子、分母的公因式是________.
6. 计算:
(1)-=________;(2)+=________;(3)·=________;
(4)÷=________;(5)-x+1=________.
知识逐点过
考点1 分式的相关概念及性质
相关概念 1. 概念:形如的式子(A,B都是整式,且B含有字母的式子,A叫做分子,B叫做分母);2. 最简分式:分子与分母没有①________的分式;3. 分式有意义的条件:②____________;4. 分式值为零的条件:③____________
基本性质 分式的分子与分母都乘(或除以)同一个不等于0的整式,分式的值④________.即= 通分(C≠0),= 约分(C≠0),其中A,B,C是整式
考点2 分式的化简及求值
1. 乘除运算
乘法 分式乘分式,用分子的积作为积的分子,分母的积作为积的分母, 即·=⑤______;
除法 分式除以分式,把除式的分子与分母颠倒位置后,与被除式相乘,即÷=·⑥______=⑦________
【温馨提示】分式乘除运算的关键是约分,即寻找分子、分母的公因式.确定公因式的方法:(1)分子、分母中能分解因式的先分解因式,(2)取分子、分母的相同因式的最低次幂的积(数字因式的最大公约数)作为公因式
2. 加减运算
同分母分式相加减:分母不变,把分子相加减:±=⑧______;异分母分式相加减:先通分,变为同分母的分式,再加减:±=±=⑨________
【温馨提示】分式加减运算的关键是通分,即寻找最简公分母.确定最简公分母的方法:(1)先观察各分母,能因式分解的先因式分解;(2)取各分母公因式(数字因式取最小公倍数)的最高次幂;(3)对于只在一个分母中含有的因式,则连同它的指数作为最简公分母的因式
3. 分式化简求值的解题步骤
步骤 (1)凡是遇见分子、分母是多项式,先因式分解,然后通分或约分;(2)有括号先计算括号里面的;(3)进行乘除计算;(4)进行加减运算;(5)代入求值
注意事项 (1)化简求值题一定要做到“先”化简,“再”求值;(2)通分时要记得给不含分母的项乘最简公分母;(3)化简结果应为最简分式或整式;(4)求值时必须保证所“代”数值使原分式的分母及运算过程中分式的分母都不为0
真题演练
命题点 分式的化简及求值
1.计算+的结果为( )
A. B. C. D.
2. 先化简,再求值:a+,其中a=5.
3. 先化简,再求值:·,其中a=.
4. 先化简,再求值:(-)÷,其中x=.
基础过关
1. 若分式有意义,则x的取值范围是( )
A. x≠-1 B. x≠0 C. x≠1 D. x≠2
2. 分式 值为0,则x的值是( )
A. 0 B. -1 C. 1 D. 0或1
3. 计算:=( )
A. a-5 B. a+5 C. 5 D. a
4. 计算-的结果等于( )
A. -1 B. x-1 C. D.
5. 化简+x-2的结果是( )
A. 1 B. C. D.
6. 化简:(1+)÷.
7. 先化简,再求值:÷(1-),其中x=-2.
先化简,再求值:(a-)÷,其中a=,b=1.
综合提升
9. 已知x2-x-1=0,计算(-)÷的值是( )
A. 1 B. -1 C. 2 D. -2
10. 已知+=,则-的值为( )
A. 1 B. 0 C. -1 D. -2
11. 先化简,再求值:÷(a+2+),其中a是使不等式≤1成立的正整数.
新考法推荐
12. (注重学习过程) 化简(+)·.下面是甲、乙两同学的部分运算过程:
第12题图
(1)甲同学解法的依据是__________,乙同学解法的依据是__________;(填序号)
①等式的基本性质;②分式的基本性质;③乘法分配律;④乘法交换律.
(2)请选择一种解法,写出完整的解答过程.
13. 下面是一道例题及其解答过程的一部分,其中M是单项式,请写出单项式M,并将该例题的解答过程补充完整.
第13题图
分 式(参考答案)
1. B 【解析】=,不是最简分式,A选项不符合题意;是最简分式,符合题意;==,不是最简分式,C选项不符合题意;==-1,不是最简分式,D选项不符合题意.
2. D
3. (1)x≠1;(2)0.
4. (1)x-1;(2)x-1(或1-x);
(3)2(x-1);(4)(x-1)2.
5. (1)2xy;(2)x+2;(3)x-3.
6. (1);(2);(3);(4)x+y;(5).
真题演练
1. C
2. 解:原式=a+(3分)
=a+a+1
=2a+1.(6分)
当a=5时,原式=2×5+1=11.(8分)
3. 解:原式=·
=
=2a.(3分)
当a=时,原式=2×=.(6分)
4. 解:原式=÷
=·
=.(4分)
当x=时,
原式===1+.(6分)
知识逐点过
①公因式 ②B≠0 ③A=0且B≠0 ④不变 ⑤ ⑥ ⑦ ⑧ ⑨
基础过关
1. A 【解析】∵分式有意义,∴x+1≠0,∴x≠-1.
2. A 【解析】∵分式的值为0,∴,解得x=0.
3. D 【解析】==a.
4. C 【解析】 原式=-==.
5. D 【解析】 原式=+==.
6. 解:原式=÷
=×
=.
7. 解: 原式=÷
=·
=-,
当x=-2时,
原式=-=-=-.
8. 解:原式=·
=·
=a-b,
当a=,b=1时,
原式=-1=-.
9. A 【解析】原式=·=·=,由x2-x-1=0,得到x2=x+1,则原式==1,故选A.
10. C 【解析】∵+==,∴ab=(a+b)(a-b).∵-====-1,∴-=-1.
11. 解:原式=÷
=·
=,
解不等式≤1,得a≤3,
该解集中的正整数有:1,2,3,
若使分式有意义,则a≠2,a≠±3,
∴a不能取2,3,∴a=1,
∴原式==-.
12. 解:(1)②,③;
(2)选择甲同学解法:
原式=[+]·
=·
=·
=2x.
选择乙同学解法:
原式=·+·
=·+·
=x-1+(x+1)
=2x.
(选择一种解法即可)
13. 解:由题意可得==,∴M=a,
则-
=-
=
=
=,
当a=100时,
原式==.
1. 下列分式中,是最简分式的是( )
A. B. C. D.
2. 下列各式中,一定正确的是( )
A. = B. = C. = D. =
3.已知分式.
(1)若分式有意义,则x的取值范围是________;
(2)若分式的值为0,则x=________.
4. 北师八下P121习题改编填空:
(1)与的最简公分母为________;
(2)与的最简公分母为________;
(3)与的最简公分母为________;
(4)与的最简公分母为________.
5. 写出下列分式中分子与分母的公因式:
(1)中分子、分母的公因式是________;
(2)中分子、分母的公因式是________;
(3)中分子、分母的公因式是________.
6. 计算:
(1)-=________;(2)+=________;(3)·=________;
(4)÷=________;(5)-x+1=________.
知识逐点过
考点1 分式的相关概念及性质
相关概念 1. 概念:形如的式子(A,B都是整式,且B含有字母的式子,A叫做分子,B叫做分母);2. 最简分式:分子与分母没有①________的分式;3. 分式有意义的条件:②____________;4. 分式值为零的条件:③____________
基本性质 分式的分子与分母都乘(或除以)同一个不等于0的整式,分式的值④________.即= 通分(C≠0),= 约分(C≠0),其中A,B,C是整式
考点2 分式的化简及求值
1. 乘除运算
乘法 分式乘分式,用分子的积作为积的分子,分母的积作为积的分母, 即·=⑤______;
除法 分式除以分式,把除式的分子与分母颠倒位置后,与被除式相乘,即÷=·⑥______=⑦________
【温馨提示】分式乘除运算的关键是约分,即寻找分子、分母的公因式.确定公因式的方法:(1)分子、分母中能分解因式的先分解因式,(2)取分子、分母的相同因式的最低次幂的积(数字因式的最大公约数)作为公因式
2. 加减运算
同分母分式相加减:分母不变,把分子相加减:±=⑧______;异分母分式相加减:先通分,变为同分母的分式,再加减:±=±=⑨________
【温馨提示】分式加减运算的关键是通分,即寻找最简公分母.确定最简公分母的方法:(1)先观察各分母,能因式分解的先因式分解;(2)取各分母公因式(数字因式取最小公倍数)的最高次幂;(3)对于只在一个分母中含有的因式,则连同它的指数作为最简公分母的因式
3. 分式化简求值的解题步骤
步骤 (1)凡是遇见分子、分母是多项式,先因式分解,然后通分或约分;(2)有括号先计算括号里面的;(3)进行乘除计算;(4)进行加减运算;(5)代入求值
注意事项 (1)化简求值题一定要做到“先”化简,“再”求值;(2)通分时要记得给不含分母的项乘最简公分母;(3)化简结果应为最简分式或整式;(4)求值时必须保证所“代”数值使原分式的分母及运算过程中分式的分母都不为0
真题演练
命题点 分式的化简及求值
1.计算+的结果为( )
A. B. C. D.
2. 先化简,再求值:a+,其中a=5.
3. 先化简,再求值:·,其中a=.
4. 先化简,再求值:(-)÷,其中x=.
基础过关
1. 若分式有意义,则x的取值范围是( )
A. x≠-1 B. x≠0 C. x≠1 D. x≠2
2. 分式 值为0,则x的值是( )
A. 0 B. -1 C. 1 D. 0或1
3. 计算:=( )
A. a-5 B. a+5 C. 5 D. a
4. 计算-的结果等于( )
A. -1 B. x-1 C. D.
5. 化简+x-2的结果是( )
A. 1 B. C. D.
6. 化简:(1+)÷.
7. 先化简,再求值:÷(1-),其中x=-2.
先化简,再求值:(a-)÷,其中a=,b=1.
综合提升
9. 已知x2-x-1=0,计算(-)÷的值是( )
A. 1 B. -1 C. 2 D. -2
10. 已知+=,则-的值为( )
A. 1 B. 0 C. -1 D. -2
11. 先化简,再求值:÷(a+2+),其中a是使不等式≤1成立的正整数.
新考法推荐
12. (注重学习过程) 化简(+)·.下面是甲、乙两同学的部分运算过程:
第12题图
(1)甲同学解法的依据是__________,乙同学解法的依据是__________;(填序号)
①等式的基本性质;②分式的基本性质;③乘法分配律;④乘法交换律.
(2)请选择一种解法,写出完整的解答过程.
13. 下面是一道例题及其解答过程的一部分,其中M是单项式,请写出单项式M,并将该例题的解答过程补充完整.
第13题图
分 式(参考答案)
1. B 【解析】=,不是最简分式,A选项不符合题意;是最简分式,符合题意;==,不是最简分式,C选项不符合题意;==-1,不是最简分式,D选项不符合题意.
2. D
3. (1)x≠1;(2)0.
4. (1)x-1;(2)x-1(或1-x);
(3)2(x-1);(4)(x-1)2.
5. (1)2xy;(2)x+2;(3)x-3.
6. (1);(2);(3);(4)x+y;(5).
真题演练
1. C
2. 解:原式=a+(3分)
=a+a+1
=2a+1.(6分)
当a=5时,原式=2×5+1=11.(8分)
3. 解:原式=·
=
=2a.(3分)
当a=时,原式=2×=.(6分)
4. 解:原式=÷
=·
=.(4分)
当x=时,
原式===1+.(6分)
知识逐点过
①公因式 ②B≠0 ③A=0且B≠0 ④不变 ⑤ ⑥ ⑦ ⑧ ⑨
基础过关
1. A 【解析】∵分式有意义,∴x+1≠0,∴x≠-1.
2. A 【解析】∵分式的值为0,∴,解得x=0.
3. D 【解析】==a.
4. C 【解析】 原式=-==.
5. D 【解析】 原式=+==.
6. 解:原式=÷
=×
=.
7. 解: 原式=÷
=·
=-,
当x=-2时,
原式=-=-=-.
8. 解:原式=·
=·
=a-b,
当a=,b=1时,
原式=-1=-.
9. A 【解析】原式=·=·=,由x2-x-1=0,得到x2=x+1,则原式==1,故选A.
10. C 【解析】∵+==,∴ab=(a+b)(a-b).∵-====-1,∴-=-1.
11. 解:原式=÷
=·
=,
解不等式≤1,得a≤3,
该解集中的正整数有:1,2,3,
若使分式有意义,则a≠2,a≠±3,
∴a不能取2,3,∴a=1,
∴原式==-.
12. 解:(1)②,③;
(2)选择甲同学解法:
原式=[+]·
=·
=·
=2x.
选择乙同学解法:
原式=·+·
=·+·
=x-1+(x+1)
=2x.
(选择一种解法即可)
13. 解:由题意可得==,∴M=a,
则-
=-
=
=
=,
当a=100时,
原式==.
同课章节目录
