3.1.3 概率的基本性质
图片预览







文档简介
课件21张PPT。3.1.3 概率的基本性质事件
的关系
和运算 概率的
几个基
本性质 思考:在掷骰子试验中,可以定义许多事件,例如:C1={出现1点};C2={出现2点};C3={出现3点};C4={出现4点};C5={出现5点};C6={出现6点};D1={出现的点数不大于1};D2={出现的点数大于3};D3={出现的点数小于5};E={出现的点数小于7};F={出现的点数大于6};G={出现的点数为偶数};H={出现的点数为奇数};类比集合与集合的关系、运算,你能发现事件之间的关系与运算吗?……(一)、事件的关系与运算对于事件A与事件B,如果事件A发生,则事件B一定发生,这时称事件B包含事件A(或称事件A包含于事件B).1.包含关系
注:(1)图形表示:(2)不可能事件记作?,任何事件都包含不可能事件。如: C1 ? ?记作:B?A(或A?B) D3={出现的点数小于5};例: C1={出现1点}; 如:D3 ? C1 或 C1 ? D3一般地,若B?A,且A?B ,那么称事件A与事
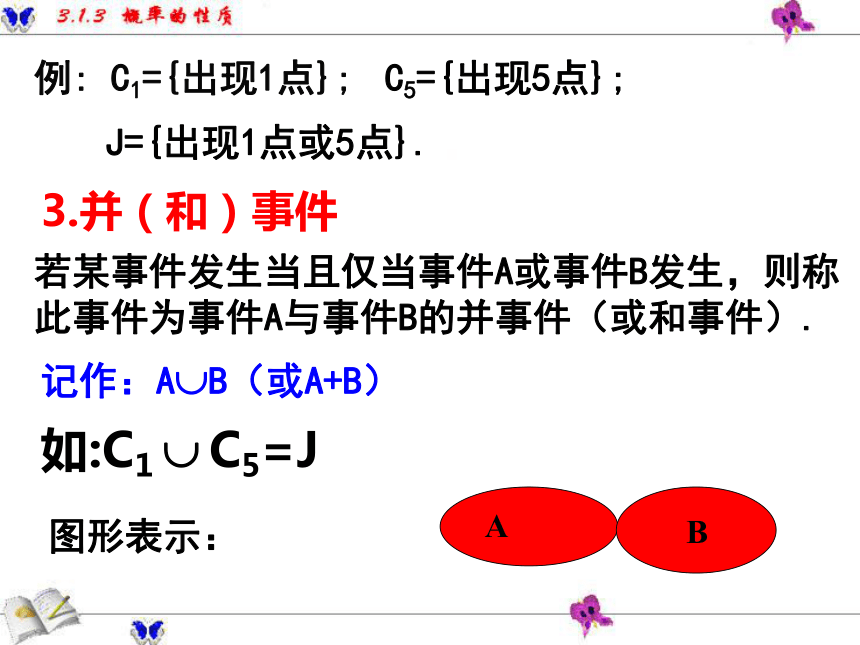
件B相等。(2)两个相等的事件总是同时发生或同时不发生。B(A)2.相等事件记作:A=B.注:(1)图形表示:例: C1={出现1点};D1={出现的点数不大于1};如: C1=D13.并(和)事件若某事件发生当且仅当事件A或事件B发生,则称此事件为事件A与事件B的并事件(或和事件).记作:A?B(或A+B)AB图形表示:例: C1={出现1点};C5={出现5点};J={出现1点或5点}.如:C1 ? C5=J4.交(积)事件若某事件发生当且仅当事件A发生且事件B发生,则称此事件为事件A与事件B的交事件(或积事件).记作:A?B(或AB)如: C3 ? D3= C4图形表示:例:C3={出现的点数大于3};D3={出现的点数小于5};C4={出现4点};5.互斥事件若A?B为不可能事件( A?B =?)那么称事件A与事件B互斥. (1)事件A与事件B在任何一次试验中不
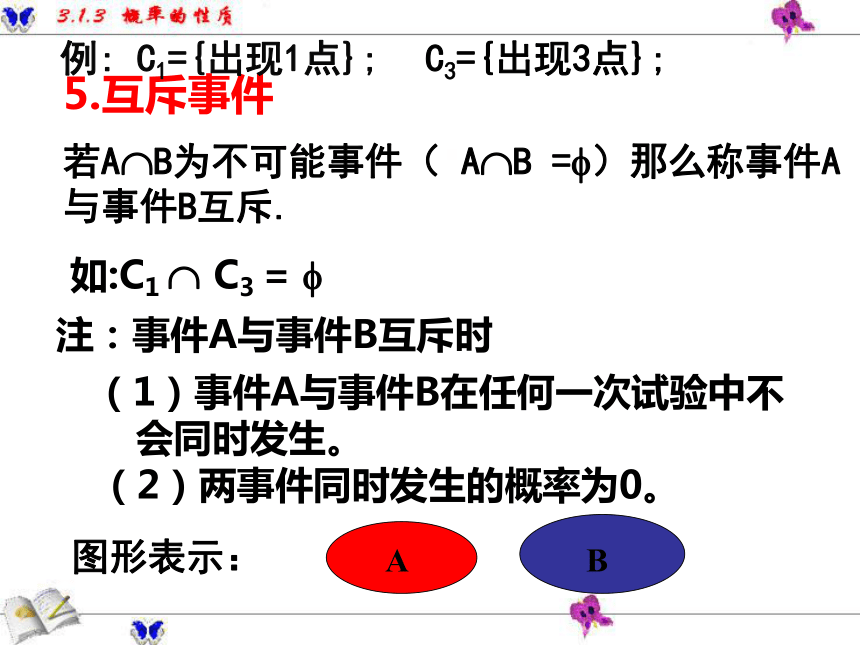
会同时发生。(2)两事件同时发生的概率为0。图形表示:例: C1={出现1点};C3={出现3点};如:C1 ? C3 = ?注:事件A与事件B互斥时(2)对立事件一定是互斥事件,但互斥 事件不一定是对立事件。6.对立事件若A?B为不可能事件, A?B为必然事件,那么事件A与事件B互为对立事件。注:(1)事件A与事件B在任何一次试验中有且
仅有一个发生。例: G={出现的点数为偶数};H={出现的点数为奇数};如:事件G与事件H互为对立事件探索:一个射手进行一次射击,试判断下列事件
哪些是互斥事件?哪些是对立事件?
事件A:命中环数大于7环;事件C:命中环数小于6环; 事件D:命中环数为6、7、8、9、10环. 事件B:命中环数为10环; 解:A与C互斥(不可能同时发生),B与C互斥,
C与D互斥,C与D是对立事件(至少一个发生) 1、某工厂为了节约用电,规定每天的用
电量指标为1000千瓦时,按照上个月的用电记录,30天中有12天的用电量超过指标,若第二个月仍没有具体的节电设施,试求该月第一天用电量超过指标概率近似值是多少?
解:0.4练习一2、一个人打靶时连续射击两次,事件“至少有一次中靶”的互斥事件是( )
(A)至少有一次中靶。(B)两次都中靶。
(C)只有一次中靶。 (D)两次都不中靶。
3、把红、蓝、黑、白4张纸牌随机分给甲、乙、丙、丁4个人,每人分得一张,事件“甲分得红牌”与事件“乙分得红牌”是( )
(A)对立事件 。 (B)互斥但不对立事件。
(C)不可能事件 。( D)以上都不是。
DB (二)、概率的几个基本性质1.概率P(A)的取值范围(1)0≤P(A)≤1.(2)必然事件的概率是1.(3)不可能事件的概率是0.思考:掷一枚骰子,事件C1={出现1点},事件
C3={出现3点}则事件C1 ? C3 发生的频率
与事件C1和事件C3发生的频率之间有什
么关系?结论:当事件A与事件B互斥时
2.概率的加法公式:如果事件A与事件B互斥,则
P(A ? B)= P(A) + P(B)若事件A,B为对立事件,则
P(B)=1-P(A)3.对立事件的概率公式(1)取到红色牌(事件C)的概率是多少?(2)取到黑色牌(事件D)的概率是多少??解(1)因为C= A∪B,且A与B不会同时发生,所以A与B是互
斥事件。根据概率的加法公式,得:
P(C)=P(A)+P(B)=1/2(2)C与D也是互斥事件,又由于 C∪D为必然事件,所以
C与D互为对立事件,所以
P(D)=1-P(C)=1/2例 某地区的年降水量在下列范围内的概率如下所示:1.求年降水量在[100,200)(㎜)范围内的概率;2.求年降水量在[150,300)(mm)范围内的概率。解:(1)记这个地区的年降水量在[100,150),[150,200),[200,250),[250,300)(mm)范围内分别为事件为A、B、C、D。这4个事件是彼此互斥的。根据互斥事件的概率加法公式,有(1)年降水量在[100,200)(mm)范围内的概率是P(A+B)=P(A)+P(B)=0.12+0.25=0.37(2)年降水量在[150,300)(mm)内的概率是P(B+C+D)=P(B)+P(C)+P(D)=0.25+0.16+0.14=0.55.
练习:学案60页举一反三3自我评价1.某射手射击一次射中10环、9环、8环、7环的概率分别是0.24、0.28、0.19、0.16,计算这名射手射击一次
(1)射中10环或9环的概率;
(2)至少射中7环的概率.
(3)射中环数不足8环的概率.2. 学案59页1、60页误区警示1、事件的关系与运算,区分互斥事件与对立事件
2、概率的基本性质
(1)对于任一事件A,有0≤P(A)≤1
(2)如果事件A与事件B互斥,则P(A ? B)= P(A) + P(B)
(3)若事件A,B为对立事件,则P(B)=1-P(A)谢谢指导!
的关系
和运算 概率的
几个基
本性质 思考:在掷骰子试验中,可以定义许多事件,例如:C1={出现1点};C2={出现2点};C3={出现3点};C4={出现4点};C5={出现5点};C6={出现6点};D1={出现的点数不大于1};D2={出现的点数大于3};D3={出现的点数小于5};E={出现的点数小于7};F={出现的点数大于6};G={出现的点数为偶数};H={出现的点数为奇数};类比集合与集合的关系、运算,你能发现事件之间的关系与运算吗?……(一)、事件的关系与运算对于事件A与事件B,如果事件A发生,则事件B一定发生,这时称事件B包含事件A(或称事件A包含于事件B).1.包含关系
注:(1)图形表示:(2)不可能事件记作?,任何事件都包含不可能事件。如: C1 ? ?记作:B?A(或A?B) D3={出现的点数小于5};例: C1={出现1点}; 如:D3 ? C1 或 C1 ? D3一般地,若B?A,且A?B ,那么称事件A与事
件B相等。(2)两个相等的事件总是同时发生或同时不发生。B(A)2.相等事件记作:A=B.注:(1)图形表示:例: C1={出现1点};D1={出现的点数不大于1};如: C1=D13.并(和)事件若某事件发生当且仅当事件A或事件B发生,则称此事件为事件A与事件B的并事件(或和事件).记作:A?B(或A+B)AB图形表示:例: C1={出现1点};C5={出现5点};J={出现1点或5点}.如:C1 ? C5=J4.交(积)事件若某事件发生当且仅当事件A发生且事件B发生,则称此事件为事件A与事件B的交事件(或积事件).记作:A?B(或AB)如: C3 ? D3= C4图形表示:例:C3={出现的点数大于3};D3={出现的点数小于5};C4={出现4点};5.互斥事件若A?B为不可能事件( A?B =?)那么称事件A与事件B互斥. (1)事件A与事件B在任何一次试验中不
会同时发生。(2)两事件同时发生的概率为0。图形表示:例: C1={出现1点};C3={出现3点};如:C1 ? C3 = ?注:事件A与事件B互斥时(2)对立事件一定是互斥事件,但互斥 事件不一定是对立事件。6.对立事件若A?B为不可能事件, A?B为必然事件,那么事件A与事件B互为对立事件。注:(1)事件A与事件B在任何一次试验中有且
仅有一个发生。例: G={出现的点数为偶数};H={出现的点数为奇数};如:事件G与事件H互为对立事件探索:一个射手进行一次射击,试判断下列事件
哪些是互斥事件?哪些是对立事件?
事件A:命中环数大于7环;事件C:命中环数小于6环; 事件D:命中环数为6、7、8、9、10环. 事件B:命中环数为10环; 解:A与C互斥(不可能同时发生),B与C互斥,
C与D互斥,C与D是对立事件(至少一个发生) 1、某工厂为了节约用电,规定每天的用
电量指标为1000千瓦时,按照上个月的用电记录,30天中有12天的用电量超过指标,若第二个月仍没有具体的节电设施,试求该月第一天用电量超过指标概率近似值是多少?
解:0.4练习一2、一个人打靶时连续射击两次,事件“至少有一次中靶”的互斥事件是( )
(A)至少有一次中靶。(B)两次都中靶。
(C)只有一次中靶。 (D)两次都不中靶。
3、把红、蓝、黑、白4张纸牌随机分给甲、乙、丙、丁4个人,每人分得一张,事件“甲分得红牌”与事件“乙分得红牌”是( )
(A)对立事件 。 (B)互斥但不对立事件。
(C)不可能事件 。( D)以上都不是。
DB (二)、概率的几个基本性质1.概率P(A)的取值范围(1)0≤P(A)≤1.(2)必然事件的概率是1.(3)不可能事件的概率是0.思考:掷一枚骰子,事件C1={出现1点},事件
C3={出现3点}则事件C1 ? C3 发生的频率
与事件C1和事件C3发生的频率之间有什
么关系?结论:当事件A与事件B互斥时
2.概率的加法公式:如果事件A与事件B互斥,则
P(A ? B)= P(A) + P(B)若事件A,B为对立事件,则
P(B)=1-P(A)3.对立事件的概率公式(1)取到红色牌(事件C)的概率是多少?(2)取到黑色牌(事件D)的概率是多少??解(1)因为C= A∪B,且A与B不会同时发生,所以A与B是互
斥事件。根据概率的加法公式,得:
P(C)=P(A)+P(B)=1/2(2)C与D也是互斥事件,又由于 C∪D为必然事件,所以
C与D互为对立事件,所以
P(D)=1-P(C)=1/2例 某地区的年降水量在下列范围内的概率如下所示:1.求年降水量在[100,200)(㎜)范围内的概率;2.求年降水量在[150,300)(mm)范围内的概率。解:(1)记这个地区的年降水量在[100,150),[150,200),[200,250),[250,300)(mm)范围内分别为事件为A、B、C、D。这4个事件是彼此互斥的。根据互斥事件的概率加法公式,有(1)年降水量在[100,200)(mm)范围内的概率是P(A+B)=P(A)+P(B)=0.12+0.25=0.37(2)年降水量在[150,300)(mm)内的概率是P(B+C+D)=P(B)+P(C)+P(D)=0.25+0.16+0.14=0.55.
练习:学案60页举一反三3自我评价1.某射手射击一次射中10环、9环、8环、7环的概率分别是0.24、0.28、0.19、0.16,计算这名射手射击一次
(1)射中10环或9环的概率;
(2)至少射中7环的概率.
(3)射中环数不足8环的概率.2. 学案59页1、60页误区警示1、事件的关系与运算,区分互斥事件与对立事件
2、概率的基本性质
(1)对于任一事件A,有0≤P(A)≤1
(2)如果事件A与事件B互斥,则P(A ? B)= P(A) + P(B)
(3)若事件A,B为对立事件,则P(B)=1-P(A)谢谢指导!
