2024年中考 数学专题提升10 一次函数的图象与性质(含答案)
文档属性
| 名称 | 2024年中考 数学专题提升10 一次函数的图象与性质(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 394.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-17 19:24:32 | ||
图片预览




文档简介
一次函数的图象与性质
1. 已知一次函数y=kx+b(k≠0),解答下列问题:
(1)若y是关于x的正比例函数,则b的值为________;
(2)当y值随x的增大而增大时,k的取值范围为________;
(3)当k<0时,若点A(x1,y1),B(x2,y2)在该函数图象上,且x1>x2,则y1________y2(填“>”“<”或“=”);
(4)若b=2k,且x每增加1,y就减少3,则k=________,b=________,此时函数经过第________象限;
(5)在(4)的条件下,该一次函数与x轴的交点坐标为________,与y轴的交点坐标为________;与坐标轴所围成的三角形的面积为________.
2. 已知一次函数y=kx+b(k≠0)的图象经过点(3,5),(-1,-3).
(1)该一次函数的解析式为________;
(2)将该函数的图象向上平移4个单位长度,得到的函数图象的解析式为________;
(3)将该函数的图象向左平移m(m>0)个单位长度后经过点(1,2),则m的值为________.
3. 已知一次函数y=kx+b(k<0)的图象与x轴相交于点(2,0).
(1)其大致图象可能是( )
(2)结合图象可知,关于x的方程kx+b=0的解为________,不等式kx+b>0的解集为________;
(3)已知一次函数y=kx+b(k<0)与一次函数y=3x-1的图象交于点(1,2).
①关于x的方程kx+b=3x-1的解为________,方程组的解为________;
②不等式kx+b<3x-1的解集为________.
知识逐点过
考点1 一次函数的图象与性质
一次函数 y=kx+b(k,b是常数,k≠0)(特别地,当b=0时,y=kx为正比例函数,图象为过原点的一条直线)
k决定图象的倾斜方向和增减性 k①__0
b决定图象与y轴的交点位置 b③______0 交点在正半轴上 b=0 交点为原点 b⑤______0 交点在负半轴上 b>0 交点在正半轴上 b⑩______0 交点为原点 b<0 交点在负半轴上
图象(草图) ④________ ⑨________
经过的象限 一、二、三 一、三 ⑥________ 一、二、四 ________ 二、三、四
与坐标轴的交点 与x轴的交点坐标为 ______(即令y=0),与y轴的交点坐标为 ______(即令x=0)
考点2 一次函数解析式的确定
常用方法 待定系数法
一般步骤 一设:设出一次函数解析式y=kx+b(k≠0);二列:找出函数图象上的两个点,代入y=kx+b,得到二元一次方程组;三解:解这个二元一次方程组,得到k,b的值;四还原:将所求待定系数k,b的值代入y=kx+b中即可
【温馨提示】对于正比例函数y=kx(k≠0),找出函数图象上的一点(非原点),代入解析式即可确定k的值
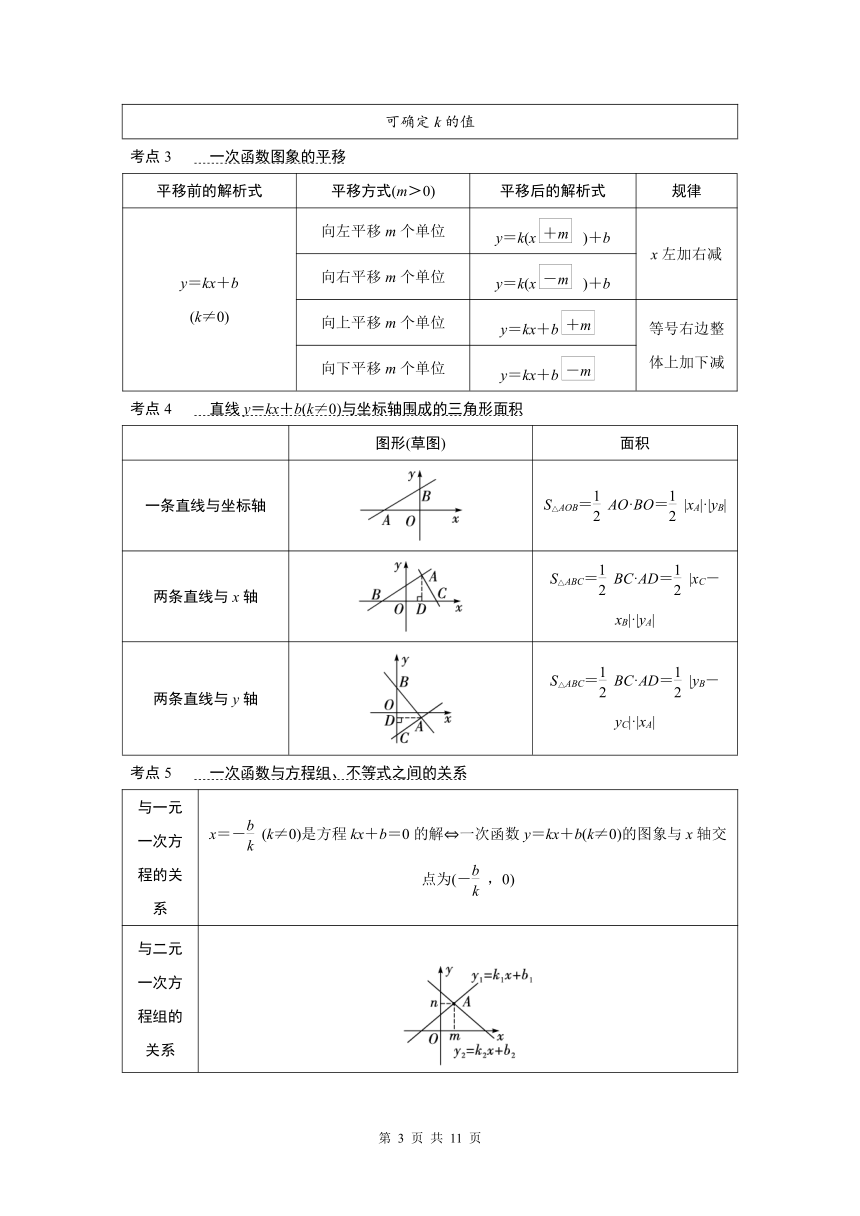
考点3 一次函数图象的平移
平移前的解析式 平移方式(m>0) 平移后的解析式 规律
y=kx+b(k≠0) 向左平移m个单位 y=k(x)+b x左加右减
向右平移m个单位 y=k(x)+b
向上平移m个单位 y=kx+b 等号右边整体上加下减
向下平移m个单位 y=kx+b
考点4 直线y=kx+b(k≠0)与坐标轴围成的三角形面积
图形(草图) 面积
一条直线与坐标轴 S△AOB=AO·BO=|xA|·|yB|
两条直线与x轴 S△ABC=BC·AD=|xC-xB|·|yA|
两条直线与y轴 S△ABC=BC·AD=|yB-yC|·|xA|
考点5 一次函数与方程组、不等式之间的关系
与一元一次方程的关系 x=-(k≠0)是方程kx+b=0的解 一次函数y=kx+b(k≠0)的图象与x轴交点为(-,0)
与二元一次方程组的关系 是二元一次方程组的解 一次函数y1=k1x+b1与y2=k2x+b2图象的交点为A(m,n)
与一元一次不等式的关系 1. 不等式kx+b>0的解集 函数y=kx+b的图象位于x轴上方部分(y>0)所对应的x的取值范围;2. 不等式kx+b<0的解集 函数y=kx+b的图象位于x轴下方部分(y<0)所对应的x的取值范围;3. 不等式kx+m>ax+b的解集就是函数y1=kx+m的图象在y2=ax+b图象上方部分所对应的x的取值范围,即x>xp;4. 不等式kx+m<ax+b的解集就是函数y1=kx+m的图象在y2=ax+b图象下方部分所对应的x的取值范围,即x<xp
真题演练
命题点1 一次函数的图象与性质
基础训练
1. 在同一平面直角坐标系中,函数y=ax和y=x+a(a为常数,a<0)的图象可能是( )
2. 已知一次函数y=x-k,若对于x<3范围内任意自变量x的值,其对应的函数值y都小于2k,则k的取值范围是________.
命题点2 一次函数解析式的确定
3. 已知一次函数y=kx+b的图象经过点(0,1)与点(2,5),求该一次函数的表达式.
基础过关
1. 下列各点在函数y=2x-1图象上的是( )
A. (-1,3) B. (0,1) C. (1,-1) D. (2,3)
2. 已知一次函数y=kx+b的图象如图所示,则k,b的取值范围是( )
A. k>0,b>0 B. k>0,b<0
C. k<0,b>0 D. k<0,b<0
第2题图
3. 关于一次函数y=x+1,下列说法正确的是( )
A. 图象经过第一、三、四象限 B. 图象与y轴交于点(0,1)
C. 函数值y随自变量x的增大而减小 D. 当x>-1时,y<0
4. 在直角坐标系中,已知点A(,m),点B(,n)是直线y=kx+b(k<0)上的两点,则m,n的大小关系是( )
A. mn C. m≥n D. m≤n
5. 在平面直角坐标系中,一次函数y=2x-3的图象是( )
ABCD
6. 如图,直线y=mx+n与y=px+q相交于点A(-2,1),则关于x的方程mx+n=px+q的解是( )
A. x=-2 B. x=1 C. x=- D. x=
第6题图
7. 如图,若直线y=kx+b与x轴交于点A(-4,0),与y轴正半轴交于点B,且△OAB的面积为4,则该直线的解析式为( )
A. y=x+2 B. y=2x+2 C. y=4x+4 D. y=x+4
第7题图
8. 一次函数y=kx-1的函数值y随x的增大而减小,当x=2时,y的值可以是( )
A. 2 B. 1 C. -1 D. -2
9. 一种弹簧秤最大能称不超过10 kg的物体,不挂物体时弹簧的长为12 cm,每挂重1 kg物体,弹簧伸长0.5 cm.在弹性限度内,挂重后弹簧的长度y(cm)与所挂物体的质量x(kg)之间的函数关系式为( )
A. y=12-0.5x B. y=12+0.5x C. y=10+0.5x D. y=0.5x
第9题图
10. 函数y=kx+3的图象经过点(2,5),则k=__________.
11.一个函数过点(1,3),且y随x增大而增大,请写出一个符合上述条件的函数解析式__________.
12. 若直线y=x向上平移3个单位长度后经过点(2,m),则m的值为__________.
13. 已知一次函数y=kx+b的图象经过点(1,3)和(-1,2),则k2-b2=__________.
综合提升
14. 已知二元一次方程组的解为,则在同一平面直角坐标系中,直线l1:y=x+5与直线l2:y=-x-1的交点坐标为( )
A. (4,1) B. (1,-4) C. (-1,-4) D. (-4,1)
15. 如图,直线y=-x+3分别与x轴,y轴交于点A,B,将△OAB绕着点A顺时针旋转90°
得到△CAD,则点B的对应点D的坐标是( )
A. (2,5) B. (3,5)
C. (5,2) D. (,2)
第15题图
16. 如图,在直角坐标系中,点A(2,m)在直线y=2x-上,过点A的直线交y轴于点B(0,3).
(1)求m的值和直线AB的函数表达式;
(2)若点P(t,y1)在线段AB上,点Q(t-1,y2)在直线y=2x-上,求y1-y2的最大值.
第16题图
一次函数的图象与性质
1. (1)0 【解析】∵正比例函数的图象是经过原点的一条直线,∴b=0.
(2)k>0 【解析】当k>0,一次函数的值y随x的增大而增大.
(3)< 【解析】当k<0,一次函数的值y随x的增大而减小,∴y1<y2.
(4)-3,-6,二、三、四 【解析】∵x每增加1,y就减少3,∴k=-3,b=2k=-6,此时函数图象经过第二、三、四象限.
(5)(-2,0),(0,-6),6 【解析】由(3)得y=-3x-6,当x=0时,解得y=-6;当y=0时,-3x-6=0,解得x=-2,∴该一次函数与x轴的交点坐标为(-2,0),与y轴的交点坐标为(0,-6),与坐标轴所围成的三角形的面积为×|-2|×|-6|=6.
2. (1)y=2x-1 【解析】∵一次函数y=kx+b的图象经过点(3,5),(-1,-3),∴,解得,∴该一次函数的解析式为y=2x-1.
(2)y=2x+3 【解析】将该函数图象向上平移4个单位长度,得到的函数图象的解析式为y=2x-1+4=2x+3.
(3) 【解析】将该函数图象向左平移m(m>0)个单位长度,得到的函数解析式为y=2(x+m)-1=2x+2m-1,∵平移后的函数图象经过点(1,2),∴2=2+2m-1,解得m=.
3. (1)A;(2)x=2,x<2;(3)①x=1,;②x>1.
知识逐点过
①> ②增大 ③> ④
⑤< ⑥一、三、四 ⑦< ⑧减小 ⑨ ⑩= 二、四 (-,0) (0,b)
真题演练
1. D
2. k≥1 【解析】∵一次函数y=x-k,∴y随x的增大而增大,∵对于x<3范围内任意自变量x的值,其对应的函数值y都小于2k,∴3-k≤2k,解得k≥1.
3. 解:将点(0,1),(2,5)代入y=kx+b中,
得,解得,(4分)
∴该一次函数的表达式为y=2x+1.(5分)
基础过关
1. D 【解析】∵当x=-1时,y=2×(-1)-1=-3,∴(-1,3)不在函数y=2x-1的图象上;∵当x=0时,y=2×0-1=-1,∴(0,1)不在函数y=2x-1的图象上;∵当x=1时,y=2×1-1=1,∴(1,-1)不在函数y=2x-1的图象上;∵当x=2时,y=2×2-1=3,∴(2,3)在函数y=2x-1的图象上.
2. B 【解析】∵一次函数图象过第一、三象限,∴k>0.又∵图象交y轴于负半轴,∴b<0.
3. B 【解析】一次函数y=x+1的图象经过第一、二、三象限,与y轴交于点(0,1),函数值y随自变量x的增大而增大,当x>-1时,y>0,故选项B符合题意.
4. A 【解析】∵y=kx+b中k<0,∴y随x的增大而减小,∵点A(,m),点B(,n)在直线y=kx+b上,且>,∴m5. D 【解析】一次函数y=2x-3中,当x=0时,y=-3,当y=0时,x=,∴一次函数y=2x-3的图象经过点(0,-3)和(,0),∴选项D符合题意.
6. A 【解析】 ∵两条直线的交点坐标为(-2,1),∴关于x的方程mx+n=px+q的解是x=-2.
7. A 【解析】 ∵A(-4,0),∴OA=4.∵S△OAB=×4OB=4,∴OB=2,∴B(0,2),把A(-4,0),B(0,2)代入y=kx+b,得,解得,∴该直线的解析式为y=x+2.
8. D 【解析】∵y随x的增大而减小,∴k<0.当x=2,y=2时,则2=2k-1,解得k=>0,A选项不符合题意;当x=2,y=1时,则1=2k-1,解得k=1>0,B选项不符合题意;当x=2,y=-1时,则-1=2k-1,解得k=0,C选项不符合题意;当x=2,y=-2时,则-2=2k-1,解得k=-<0,D选项符合题意.
9. B 【解析】∵在弹性限度内,每挂重1 kg物体,弹簧伸长0.5 cm,∴挂重后弹簧的长度y(cm)与所挂物体质量x(kg)满足一次函数关系,故设y与x之间的函数关系式为y=kx+b(k≠0).∵不挂物体时弹簧的长度为12 cm,∴当x=0时,y=12.∵每挂重1 kg物体,弹簧伸长0.5 cm,∴当x=1时,y=12.5.将(0,12)和(1,12.5)分别代入y=kx+b,得,解得,∴挂重后弹簧的长度y(cm)与所挂物体的质量x(kg)之间的函数关系式为y=12+0.5x.
10. 1 【解析】 将点(2,5)代入y=kx+3中,得5=2k+3,解得k=1.
11. y=3x(答案不唯一)
12. 5 【解析】直线y=x向上平移3个单位长度得平移后的直线解析式为y=x+3,当x=2时,m=2+3=5.
13. -6 【解析】∵一次函数y=kx+b的图象经过点(1,3)和(-1,2),则有,即,∴k2-b2=(k+b)(k-b)=3×(-2)=-6.
14. D 【解析】∵二元一次方程组的解为,∴直线l1:y=x+5与直线l2:y=-x-1的交点坐标为(-4,1).
15. C 【解析】∵直线y=-x+3分别与x轴,y轴交于点A,B,∴A(2,0),B(0,3),∴OA=2,OB=3.∵△ACD是△AOB绕点A顺时针旋转90°得到,∴AC=OA=2,CD=OB=3,∠OAC=90°,∠ACD=90°,∴点D的坐标为(5,2).
16. 解:(1)把点A(2,m)代入y=2x-,得m=,
∴A(2,),
设直线AB的函数表达式为y=kx+b(k≠0),
把点A(2,),B(0,3)代入,
得,解得,
∴直线AB的函数表达式为y=-x+3;
(2)∵点P(t,y1)在线段AB上,点Q(t-1,y2)在直线y=2x-上,
∴y1=-t+3(0≤t≤2),
y2=2(t-1)-=2t-,
∴y1-y2=-t+3-(2t-)=-t+,
∵-<0,
∴y1-y2的值随t的增大而减小,
∵0≤t≤2,
∴当t=0时,y1-y2有最大值,最大值为.
1. 已知一次函数y=kx+b(k≠0),解答下列问题:
(1)若y是关于x的正比例函数,则b的值为________;
(2)当y值随x的增大而增大时,k的取值范围为________;
(3)当k<0时,若点A(x1,y1),B(x2,y2)在该函数图象上,且x1>x2,则y1________y2(填“>”“<”或“=”);
(4)若b=2k,且x每增加1,y就减少3,则k=________,b=________,此时函数经过第________象限;
(5)在(4)的条件下,该一次函数与x轴的交点坐标为________,与y轴的交点坐标为________;与坐标轴所围成的三角形的面积为________.
2. 已知一次函数y=kx+b(k≠0)的图象经过点(3,5),(-1,-3).
(1)该一次函数的解析式为________;
(2)将该函数的图象向上平移4个单位长度,得到的函数图象的解析式为________;
(3)将该函数的图象向左平移m(m>0)个单位长度后经过点(1,2),则m的值为________.
3. 已知一次函数y=kx+b(k<0)的图象与x轴相交于点(2,0).
(1)其大致图象可能是( )
(2)结合图象可知,关于x的方程kx+b=0的解为________,不等式kx+b>0的解集为________;
(3)已知一次函数y=kx+b(k<0)与一次函数y=3x-1的图象交于点(1,2).
①关于x的方程kx+b=3x-1的解为________,方程组的解为________;
②不等式kx+b<3x-1的解集为________.
知识逐点过
考点1 一次函数的图象与性质
一次函数 y=kx+b(k,b是常数,k≠0)(特别地,当b=0时,y=kx为正比例函数,图象为过原点的一条直线)
k决定图象的倾斜方向和增减性 k①__0
b决定图象与y轴的交点位置 b③______0 交点在正半轴上 b=0 交点为原点 b⑤______0 交点在负半轴上 b>0 交点在正半轴上 b⑩______0 交点为原点 b<0 交点在负半轴上
图象(草图) ④________ ⑨________
经过的象限 一、二、三 一、三 ⑥________ 一、二、四 ________ 二、三、四
与坐标轴的交点 与x轴的交点坐标为 ______(即令y=0),与y轴的交点坐标为 ______(即令x=0)
考点2 一次函数解析式的确定
常用方法 待定系数法
一般步骤 一设:设出一次函数解析式y=kx+b(k≠0);二列:找出函数图象上的两个点,代入y=kx+b,得到二元一次方程组;三解:解这个二元一次方程组,得到k,b的值;四还原:将所求待定系数k,b的值代入y=kx+b中即可
【温馨提示】对于正比例函数y=kx(k≠0),找出函数图象上的一点(非原点),代入解析式即可确定k的值
考点3 一次函数图象的平移
平移前的解析式 平移方式(m>0) 平移后的解析式 规律
y=kx+b(k≠0) 向左平移m个单位 y=k(x)+b x左加右减
向右平移m个单位 y=k(x)+b
向上平移m个单位 y=kx+b 等号右边整体上加下减
向下平移m个单位 y=kx+b
考点4 直线y=kx+b(k≠0)与坐标轴围成的三角形面积
图形(草图) 面积
一条直线与坐标轴 S△AOB=AO·BO=|xA|·|yB|
两条直线与x轴 S△ABC=BC·AD=|xC-xB|·|yA|
两条直线与y轴 S△ABC=BC·AD=|yB-yC|·|xA|
考点5 一次函数与方程组、不等式之间的关系
与一元一次方程的关系 x=-(k≠0)是方程kx+b=0的解 一次函数y=kx+b(k≠0)的图象与x轴交点为(-,0)
与二元一次方程组的关系 是二元一次方程组的解 一次函数y1=k1x+b1与y2=k2x+b2图象的交点为A(m,n)
与一元一次不等式的关系 1. 不等式kx+b>0的解集 函数y=kx+b的图象位于x轴上方部分(y>0)所对应的x的取值范围;2. 不等式kx+b<0的解集 函数y=kx+b的图象位于x轴下方部分(y<0)所对应的x的取值范围;3. 不等式kx+m>ax+b的解集就是函数y1=kx+m的图象在y2=ax+b图象上方部分所对应的x的取值范围,即x>xp;4. 不等式kx+m<ax+b的解集就是函数y1=kx+m的图象在y2=ax+b图象下方部分所对应的x的取值范围,即x<xp
真题演练
命题点1 一次函数的图象与性质
基础训练
1. 在同一平面直角坐标系中,函数y=ax和y=x+a(a为常数,a<0)的图象可能是( )
2. 已知一次函数y=x-k,若对于x<3范围内任意自变量x的值,其对应的函数值y都小于2k,则k的取值范围是________.
命题点2 一次函数解析式的确定
3. 已知一次函数y=kx+b的图象经过点(0,1)与点(2,5),求该一次函数的表达式.
基础过关
1. 下列各点在函数y=2x-1图象上的是( )
A. (-1,3) B. (0,1) C. (1,-1) D. (2,3)
2. 已知一次函数y=kx+b的图象如图所示,则k,b的取值范围是( )
A. k>0,b>0 B. k>0,b<0
C. k<0,b>0 D. k<0,b<0
第2题图
3. 关于一次函数y=x+1,下列说法正确的是( )
A. 图象经过第一、三、四象限 B. 图象与y轴交于点(0,1)
C. 函数值y随自变量x的增大而减小 D. 当x>-1时,y<0
4. 在直角坐标系中,已知点A(,m),点B(,n)是直线y=kx+b(k<0)上的两点,则m,n的大小关系是( )
A. m
5. 在平面直角坐标系中,一次函数y=2x-3的图象是( )
ABCD
6. 如图,直线y=mx+n与y=px+q相交于点A(-2,1),则关于x的方程mx+n=px+q的解是( )
A. x=-2 B. x=1 C. x=- D. x=
第6题图
7. 如图,若直线y=kx+b与x轴交于点A(-4,0),与y轴正半轴交于点B,且△OAB的面积为4,则该直线的解析式为( )
A. y=x+2 B. y=2x+2 C. y=4x+4 D. y=x+4
第7题图
8. 一次函数y=kx-1的函数值y随x的增大而减小,当x=2时,y的值可以是( )
A. 2 B. 1 C. -1 D. -2
9. 一种弹簧秤最大能称不超过10 kg的物体,不挂物体时弹簧的长为12 cm,每挂重1 kg物体,弹簧伸长0.5 cm.在弹性限度内,挂重后弹簧的长度y(cm)与所挂物体的质量x(kg)之间的函数关系式为( )
A. y=12-0.5x B. y=12+0.5x C. y=10+0.5x D. y=0.5x
第9题图
10. 函数y=kx+3的图象经过点(2,5),则k=__________.
11.一个函数过点(1,3),且y随x增大而增大,请写出一个符合上述条件的函数解析式__________.
12. 若直线y=x向上平移3个单位长度后经过点(2,m),则m的值为__________.
13. 已知一次函数y=kx+b的图象经过点(1,3)和(-1,2),则k2-b2=__________.
综合提升
14. 已知二元一次方程组的解为,则在同一平面直角坐标系中,直线l1:y=x+5与直线l2:y=-x-1的交点坐标为( )
A. (4,1) B. (1,-4) C. (-1,-4) D. (-4,1)
15. 如图,直线y=-x+3分别与x轴,y轴交于点A,B,将△OAB绕着点A顺时针旋转90°
得到△CAD,则点B的对应点D的坐标是( )
A. (2,5) B. (3,5)
C. (5,2) D. (,2)
第15题图
16. 如图,在直角坐标系中,点A(2,m)在直线y=2x-上,过点A的直线交y轴于点B(0,3).
(1)求m的值和直线AB的函数表达式;
(2)若点P(t,y1)在线段AB上,点Q(t-1,y2)在直线y=2x-上,求y1-y2的最大值.
第16题图
一次函数的图象与性质
1. (1)0 【解析】∵正比例函数的图象是经过原点的一条直线,∴b=0.
(2)k>0 【解析】当k>0,一次函数的值y随x的增大而增大.
(3)< 【解析】当k<0,一次函数的值y随x的增大而减小,∴y1<y2.
(4)-3,-6,二、三、四 【解析】∵x每增加1,y就减少3,∴k=-3,b=2k=-6,此时函数图象经过第二、三、四象限.
(5)(-2,0),(0,-6),6 【解析】由(3)得y=-3x-6,当x=0时,解得y=-6;当y=0时,-3x-6=0,解得x=-2,∴该一次函数与x轴的交点坐标为(-2,0),与y轴的交点坐标为(0,-6),与坐标轴所围成的三角形的面积为×|-2|×|-6|=6.
2. (1)y=2x-1 【解析】∵一次函数y=kx+b的图象经过点(3,5),(-1,-3),∴,解得,∴该一次函数的解析式为y=2x-1.
(2)y=2x+3 【解析】将该函数图象向上平移4个单位长度,得到的函数图象的解析式为y=2x-1+4=2x+3.
(3) 【解析】将该函数图象向左平移m(m>0)个单位长度,得到的函数解析式为y=2(x+m)-1=2x+2m-1,∵平移后的函数图象经过点(1,2),∴2=2+2m-1,解得m=.
3. (1)A;(2)x=2,x<2;(3)①x=1,;②x>1.
知识逐点过
①> ②增大 ③> ④
⑤< ⑥一、三、四 ⑦< ⑧减小 ⑨ ⑩= 二、四 (-,0) (0,b)
真题演练
1. D
2. k≥1 【解析】∵一次函数y=x-k,∴y随x的增大而增大,∵对于x<3范围内任意自变量x的值,其对应的函数值y都小于2k,∴3-k≤2k,解得k≥1.
3. 解:将点(0,1),(2,5)代入y=kx+b中,
得,解得,(4分)
∴该一次函数的表达式为y=2x+1.(5分)
基础过关
1. D 【解析】∵当x=-1时,y=2×(-1)-1=-3,∴(-1,3)不在函数y=2x-1的图象上;∵当x=0时,y=2×0-1=-1,∴(0,1)不在函数y=2x-1的图象上;∵当x=1时,y=2×1-1=1,∴(1,-1)不在函数y=2x-1的图象上;∵当x=2时,y=2×2-1=3,∴(2,3)在函数y=2x-1的图象上.
2. B 【解析】∵一次函数图象过第一、三象限,∴k>0.又∵图象交y轴于负半轴,∴b<0.
3. B 【解析】一次函数y=x+1的图象经过第一、二、三象限,与y轴交于点(0,1),函数值y随自变量x的增大而增大,当x>-1时,y>0,故选项B符合题意.
4. A 【解析】∵y=kx+b中k<0,∴y随x的增大而减小,∵点A(,m),点B(,n)在直线y=kx+b上,且>,∴m
6. A 【解析】 ∵两条直线的交点坐标为(-2,1),∴关于x的方程mx+n=px+q的解是x=-2.
7. A 【解析】 ∵A(-4,0),∴OA=4.∵S△OAB=×4OB=4,∴OB=2,∴B(0,2),把A(-4,0),B(0,2)代入y=kx+b,得,解得,∴该直线的解析式为y=x+2.
8. D 【解析】∵y随x的增大而减小,∴k<0.当x=2,y=2时,则2=2k-1,解得k=>0,A选项不符合题意;当x=2,y=1时,则1=2k-1,解得k=1>0,B选项不符合题意;当x=2,y=-1时,则-1=2k-1,解得k=0,C选项不符合题意;当x=2,y=-2时,则-2=2k-1,解得k=-<0,D选项符合题意.
9. B 【解析】∵在弹性限度内,每挂重1 kg物体,弹簧伸长0.5 cm,∴挂重后弹簧的长度y(cm)与所挂物体质量x(kg)满足一次函数关系,故设y与x之间的函数关系式为y=kx+b(k≠0).∵不挂物体时弹簧的长度为12 cm,∴当x=0时,y=12.∵每挂重1 kg物体,弹簧伸长0.5 cm,∴当x=1时,y=12.5.将(0,12)和(1,12.5)分别代入y=kx+b,得,解得,∴挂重后弹簧的长度y(cm)与所挂物体的质量x(kg)之间的函数关系式为y=12+0.5x.
10. 1 【解析】 将点(2,5)代入y=kx+3中,得5=2k+3,解得k=1.
11. y=3x(答案不唯一)
12. 5 【解析】直线y=x向上平移3个单位长度得平移后的直线解析式为y=x+3,当x=2时,m=2+3=5.
13. -6 【解析】∵一次函数y=kx+b的图象经过点(1,3)和(-1,2),则有,即,∴k2-b2=(k+b)(k-b)=3×(-2)=-6.
14. D 【解析】∵二元一次方程组的解为,∴直线l1:y=x+5与直线l2:y=-x-1的交点坐标为(-4,1).
15. C 【解析】∵直线y=-x+3分别与x轴,y轴交于点A,B,∴A(2,0),B(0,3),∴OA=2,OB=3.∵△ACD是△AOB绕点A顺时针旋转90°得到,∴AC=OA=2,CD=OB=3,∠OAC=90°,∠ACD=90°,∴点D的坐标为(5,2).
16. 解:(1)把点A(2,m)代入y=2x-,得m=,
∴A(2,),
设直线AB的函数表达式为y=kx+b(k≠0),
把点A(2,),B(0,3)代入,
得,解得,
∴直线AB的函数表达式为y=-x+3;
(2)∵点P(t,y1)在线段AB上,点Q(t-1,y2)在直线y=2x-上,
∴y1=-t+3(0≤t≤2),
y2=2(t-1)-=2t-,
∴y1-y2=-t+3-(2t-)=-t+,
∵-<0,
∴y1-y2的值随t的增大而减小,
∵0≤t≤2,
∴当t=0时,y1-y2有最大值,最大值为.
同课章节目录
