2.1圆的对称性课件(共40张PPT)2023-2024学年度湘教版数学九年级下册
文档属性
| 名称 | 2.1圆的对称性课件(共40张PPT)2023-2024学年度湘教版数学九年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 16.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-18 14:12:28 | ||
图片预览








文档简介
(共40张PPT)
2.1 圆的对称性
九年级下
湘教版
1.了解圆及其相关概念:圆,圆心,半径,圆内的点,圆外的点,弦,直径,圆弧,劣弧,优弧,等圆,等弧;
2.初步了解点与圆的位置关系.
3.掌握圆的对称性;
学习目标
重点
难点
新课引入
在生活中,我们经常看到圆的形象.
请同学们在草稿纸上用圆规画圆,体验画圆的过程,想想圆是怎样形成的.
通过用绳子和圆规画圆的过程,你发现了什么?
由此你能得到什么结论?
点击视频播放
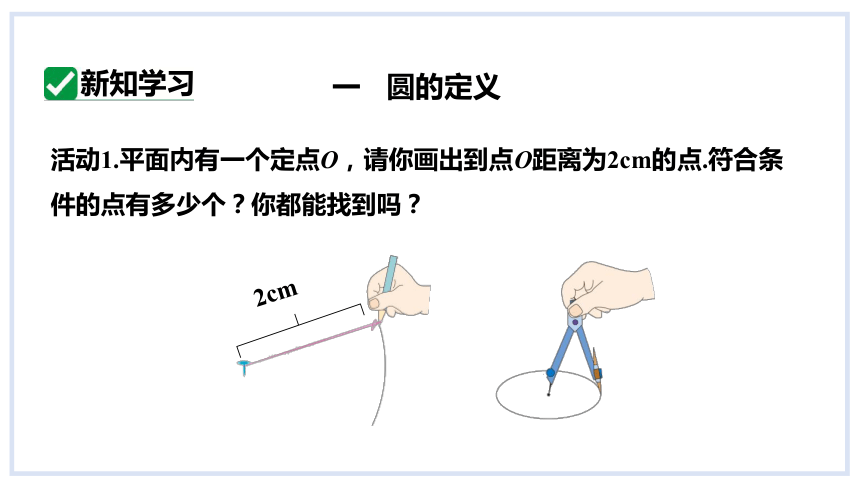
活动1.平面内有一个定点O,请你画出到点O距离为2cm的点.符合条件的点有多少个?你都能找到吗?
新知学习
一 圆的定义
2cm
圆是平面内到一定点的距离等于定长的所有点组成的图形.
这个定点叫作圆心,定长叫作半径.
思考
通过刚才的操作、观察,你能尝试说一说什么叫“圆”吗?
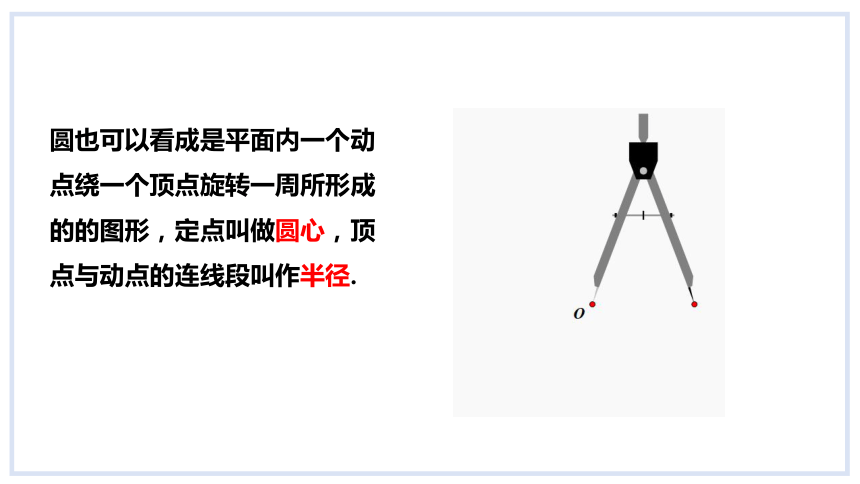
圆也可以看成是平面内一个动点绕一个顶点旋转一周所形成的的图形,定点叫做圆心,顶点与动点的连线段叫作半径.
温馨提示
1.确定一个圆需要“两个要素”,一是圆心:圆心定其位置,二是半径:半径定其大小.
2.圆是一条封闭的曲线,曲线是“圆周”,而不能认为是“圆面”.
3.“ 圆上的点”指圆周上的点.
4.到定点的距离等于定长的点都在同一个圆上
例1 下列关于圆的叙述正确的是( )
A.圆是由圆心唯一确定的
B.圆是一条封闭的曲线
C.到定点的距离小于或等于定长的所有点组成圆
D.圆内任意一点到圆心的距离都相等
B
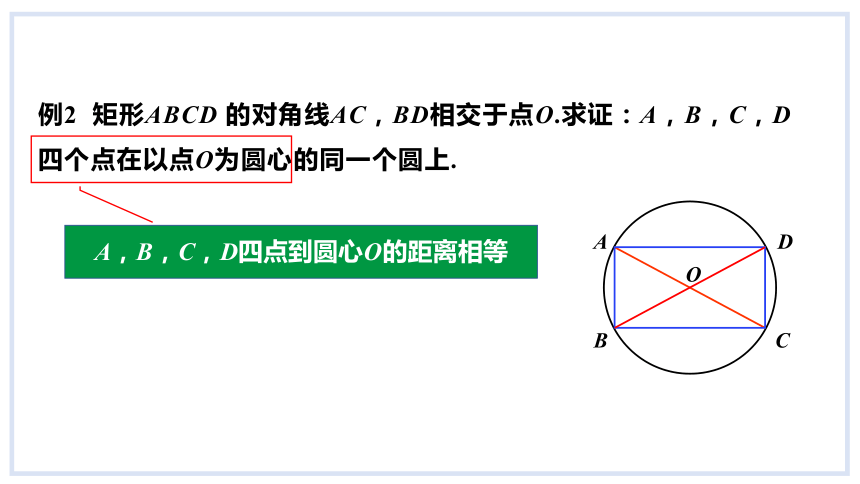
例2 矩形ABCD 的对角线AC,BD相交于点O.求证:A,B,C,D 四个点在以点O为圆心的同一个圆上.
A
B
C
D
O
A,B,C,D四点到圆心O的距离相等
A
B
C
D
O
证明:∵四边形ABCD为矩形,
∴OA=OC= AC,OB=OD= BD,AC=BD.
∴OA=OC=OB=OD.
∴A,B,C,D四个点在以点O为圆心,OA为半径的圆上.
用定义证明几个点在同一个圆上的方法:
只要证明这几个点到圆心的距离相等即可.
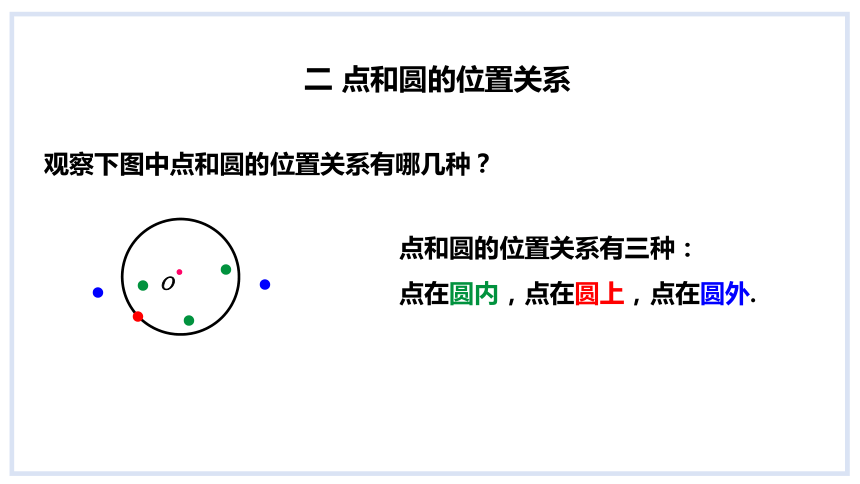
观察下图中点和圆的位置关系有哪几种?
.
o
.
.
.
.
.
.
点和圆的位置关系有三种:
点在圆内,点在圆上,点在圆外.
二 点和圆的位置关系
怎样确定点与圆的位置关系?
一般地, 设⊙O的半径为 r, 点 P 到圆心 O 的距离 OP = d ,则有:
(1) 点 P 在圆内 d < r;
(2) 点 P 在圆上 d = r;
(3) 点 P 在圆外 d > r.
我们把到圆心的距离小于半径的点叫作圆内的点;
到圆心的距离大于半径的点叫作圆外的点.
到圆心的距离等于半径的点叫作圆上的点
点与圆的位置关系有三种:
点在圆外 d>r
点在圆上 d=r
点在圆内 d温馨提示
左端可以推出右端,从右端也可以推出左端
数形结合:
位置关系
数量关系
例1 已知⊙O的面积为25π.
( 1)若PO=5.5,则点P在______;
(2)若PO=4,则点P在______;
(3)若PO=______,则点P在⊙O上.
⊙O外
⊙O内
5
例2 已知⊙O 的半径为 4 cm,B 为线段 OA 的中点,当线段
OA 满足下列条件时,分别指出点 B 与⊙O 的位置关系:
(1) OA= 6 cm; (2) OA= 8 cm; (3) OA= 10 cm.
点 B 在圆内
点 B 在圆上
点 B 在圆外
O
A
B
C
D
连接圆上任意两点的线段叫作弦,
经过圆心的弦叫作直径.
线段 AB, CD 是⊙O 的弦, 弦AB 经过圆心 O, 因此线段 AB 是 ⊙O 的直径.
三 与圆有关的概念
注意:1.弦和直径都是线段.
2.直径是弦,是经过圆心的特殊弦,是圆中最长的弦,但弦不一定是直径.
探究
圆中最长的弦是什么?为什么?
O
B
O
A
B
O
A
B
O
A
B
C
O
A
B
C
D
O
A
B
C
D
根据三角形的三边关系可判断:圆中最长的弦是直径.
AC=AO+OB>AB
CD=AO+OB>AB
CD=AO+OB>AB
圆上任意两点间的部分叫作圆弧, 简称弧,弧用符号“ ”表示.
⊙O 上两点A, B 间小于半圆的部分叫作劣弧, 记作 ;
⊙O 上两点A, B 间大于半圆的部分叫作优弧, 记作 .
1. 在一块硬纸板和一张薄的白纸上分别画一个圆,使它们的半径相等,把白纸放在硬纸板上面, 使两个圆的圆心重合,观察这两个圆是否重合.
探究
2. 用一根大头针穿过上述两个圆的圆心. 让硬纸板保持不动,让白纸绕圆心旋转任意角度. 观察旋转后白纸上的圆是否仍然与硬纸板上的圆重合. 这体现圆具有什么样的性质?
能够重合的两个圆叫做等圆.
注:半径相等的两个圆是等圆, 反过来,同圆或等圆的半径相等.
一个圆上两个弧重合或两个等圆上两个弧重合称之为等弧。
注: ①等弧是全等的,不仅是弧的长度相等.
②等弧只存在于同圆或等圆中.
等圆
半径相同,圆心不同.
同心圆
圆心相同,半径不同。
·
C
O
A
·
C
O1
A
·
C
O
A
3.同圆是等圆吗?
不是
“等弧”不等于“长度相等的弧”,等弧仅仅存在于同圆或等圆中.
D
C
A
B
想一想,长度相等的弧是等弧吗?
如图,AB和CD的拉直长度都是10 cm,平移并调整小圆的位置,这两条弧不可能完全重合,因为这两条弧弯曲程度不同.
(
(
等弧:在同圆或等圆中,能够互相重合的弧叫做等弧.
例1 以下命题:(1)半圆是弧,但弧不一定是半圆;(2)过圆上任意一点只能作一条弦,且这条弦是直径;(3)弦是直径;(4)直径是圆中最长的弦;(5)直径不是弦;(6)优弧大于劣弧;(7)以O为圆心可以画无数个圆. 正确的个数为( )
A.1 B.2 C.3 D.4
C
例2 如图, 在☉O 中,点 A , O , D 以及点 B , O , C 分别在
同一条直线上, 图中弦的条数为( )
A. 2 B. 3 C. 4 D.5
A
四 圆的对称性
(1)圆是轴对称图形吗?如果是,它的对称轴是什么?你能找到多少条对称轴?
(2)你是怎么得出结论的?
用折叠的方法
●O
思考
圆是轴对称图形,其对称轴是任意一条直径所在的直线,可以找到无数条对称轴.
在纸上任画一个⊙O, 并剪下来. 将⊙O 沿任意一条直径(例如直径CD) 对折, 你发现了什么?
讨论
直径CD两侧的两个半圆能完全重合
圆是轴对称图形, 任意一条直径所在的直线都是圆的对称轴.
重合,圆是中心对称图形
.
O
A
B
180°
问题1 将圆绕圆心旋转180°后,得到的图形与原图形重合吗?由此你得到什么结论呢?
探究
问题2 把圆绕圆心旋转任意一个角度呢?仍与原来的圆重合吗?
O
α
重合,圆是旋转对称图形,无论绕圆心旋转多少度,它都能与自身重合,对称中心即为其圆心.
·
1. 圆有无数条对称轴,但只有一个对称中心.
2. 因为直径是弦,弦是线段,而对称轴是直线,所以说“圆的对称轴是直径所在的直线”或说成“圆的对称轴是经过圆心的直线”.
温馨提示
为什么通常要把车轮设计成圆形? 请说说理由.
古代车轮的演变
议一议
圆形车轮转动到任何一个角度,圆心到地面的距离都不变使车轮在滚动时很平滑
例1 下列说法中正确的是( )
A. 圆的任意一条直径都是它的对称轴
B. 经过圆心的直线是圆的对称轴
C. 与圆相交的直线是圆的对称轴
D. 与半径垂直的直线是圆的对称轴
B
1.下列关于圆的说法,正确的是( )
A.在平面内圆是所有到定点距离等于定长的点的集合
B.同一平面内两个半径相等的圆必定关于某一条直线成轴对称
C.优弧大于劣弧
D.圆绕圆心旋转任意角度都与自身重合
随堂练习
ABD
2.下列说法中正确的有( )
(1)圆是轴对称图形;(2)圆是旋转对称图形;(3)圆不是中心对称图形;(4)圆是轴对称图形但不是旋转对称图形.
A.1个 B.2个
C.3个 D.4个
B
3.已知⊙O的半径为2、AB是⊙O的一条弦,则 AB的长不可能是( )
A. 2 B. 3
C.4 D.5
D
4. 已知☉O 的半径为 6 cm , P 为线段 OA 的中点,若点 P
在☉O 上,则 OA 的长( )
A. 等于 6 cm B. 等于 12 cm
C. 小于 6 cm D. 大于 12 cm
B
5.如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,E、F分别是AB、AC的中点.以点B为圆心,BC为半径画圆,判断点A、 C、E、F与⊙B的位置关系,并说明理由.
A
B
C
E
F
解:连接BF. C在⊙B上;在直角△ABC中,
AB=
则A在⊙B的外部;
BE= AB= ×5= <3=BC,则E在⊙B内部;
CP= AC= ×4=2,则在直角△BCF中,
BF= ,则F在⊙B的外部.
圆
定义
旋转定义:要画一个确定的圆,关键是确定圆心和半径
集合定义:同圆半径相等
弦:直径是圆中最长的弦
弧:劣弧、半圆、优弧.
有关概念
点在圆外 d > r.
点在圆上 d = r.
点在圆内 d < r.
点与圆的
位置关系
课堂小结
圆的对称性
圆是轴对称图形
圆是中心对称图形
2.1 圆的对称性
九年级下
湘教版
1.了解圆及其相关概念:圆,圆心,半径,圆内的点,圆外的点,弦,直径,圆弧,劣弧,优弧,等圆,等弧;
2.初步了解点与圆的位置关系.
3.掌握圆的对称性;
学习目标
重点
难点
新课引入
在生活中,我们经常看到圆的形象.
请同学们在草稿纸上用圆规画圆,体验画圆的过程,想想圆是怎样形成的.
通过用绳子和圆规画圆的过程,你发现了什么?
由此你能得到什么结论?
点击视频播放
活动1.平面内有一个定点O,请你画出到点O距离为2cm的点.符合条件的点有多少个?你都能找到吗?
新知学习
一 圆的定义
2cm
圆是平面内到一定点的距离等于定长的所有点组成的图形.
这个定点叫作圆心,定长叫作半径.
思考
通过刚才的操作、观察,你能尝试说一说什么叫“圆”吗?
圆也可以看成是平面内一个动点绕一个顶点旋转一周所形成的的图形,定点叫做圆心,顶点与动点的连线段叫作半径.
温馨提示
1.确定一个圆需要“两个要素”,一是圆心:圆心定其位置,二是半径:半径定其大小.
2.圆是一条封闭的曲线,曲线是“圆周”,而不能认为是“圆面”.
3.“ 圆上的点”指圆周上的点.
4.到定点的距离等于定长的点都在同一个圆上
例1 下列关于圆的叙述正确的是( )
A.圆是由圆心唯一确定的
B.圆是一条封闭的曲线
C.到定点的距离小于或等于定长的所有点组成圆
D.圆内任意一点到圆心的距离都相等
B
例2 矩形ABCD 的对角线AC,BD相交于点O.求证:A,B,C,D 四个点在以点O为圆心的同一个圆上.
A
B
C
D
O
A,B,C,D四点到圆心O的距离相等
A
B
C
D
O
证明:∵四边形ABCD为矩形,
∴OA=OC= AC,OB=OD= BD,AC=BD.
∴OA=OC=OB=OD.
∴A,B,C,D四个点在以点O为圆心,OA为半径的圆上.
用定义证明几个点在同一个圆上的方法:
只要证明这几个点到圆心的距离相等即可.
观察下图中点和圆的位置关系有哪几种?
.
o
.
.
.
.
.
.
点和圆的位置关系有三种:
点在圆内,点在圆上,点在圆外.
二 点和圆的位置关系
怎样确定点与圆的位置关系?
一般地, 设⊙O的半径为 r, 点 P 到圆心 O 的距离 OP = d ,则有:
(1) 点 P 在圆内 d < r;
(2) 点 P 在圆上 d = r;
(3) 点 P 在圆外 d > r.
我们把到圆心的距离小于半径的点叫作圆内的点;
到圆心的距离大于半径的点叫作圆外的点.
到圆心的距离等于半径的点叫作圆上的点
点与圆的位置关系有三种:
点在圆外 d>r
点在圆上 d=r
点在圆内 d
左端可以推出右端,从右端也可以推出左端
数形结合:
位置关系
数量关系
例1 已知⊙O的面积为25π.
( 1)若PO=5.5,则点P在______;
(2)若PO=4,则点P在______;
(3)若PO=______,则点P在⊙O上.
⊙O外
⊙O内
5
例2 已知⊙O 的半径为 4 cm,B 为线段 OA 的中点,当线段
OA 满足下列条件时,分别指出点 B 与⊙O 的位置关系:
(1) OA= 6 cm; (2) OA= 8 cm; (3) OA= 10 cm.
点 B 在圆内
点 B 在圆上
点 B 在圆外
O
A
B
C
D
连接圆上任意两点的线段叫作弦,
经过圆心的弦叫作直径.
线段 AB, CD 是⊙O 的弦, 弦AB 经过圆心 O, 因此线段 AB 是 ⊙O 的直径.
三 与圆有关的概念
注意:1.弦和直径都是线段.
2.直径是弦,是经过圆心的特殊弦,是圆中最长的弦,但弦不一定是直径.
探究
圆中最长的弦是什么?为什么?
O
B
O
A
B
O
A
B
O
A
B
C
O
A
B
C
D
O
A
B
C
D
根据三角形的三边关系可判断:圆中最长的弦是直径.
AC=AO+OB>AB
CD=AO+OB>AB
CD=AO+OB>AB
圆上任意两点间的部分叫作圆弧, 简称弧,弧用符号“ ”表示.
⊙O 上两点A, B 间小于半圆的部分叫作劣弧, 记作 ;
⊙O 上两点A, B 间大于半圆的部分叫作优弧, 记作 .
1. 在一块硬纸板和一张薄的白纸上分别画一个圆,使它们的半径相等,把白纸放在硬纸板上面, 使两个圆的圆心重合,观察这两个圆是否重合.
探究
2. 用一根大头针穿过上述两个圆的圆心. 让硬纸板保持不动,让白纸绕圆心旋转任意角度. 观察旋转后白纸上的圆是否仍然与硬纸板上的圆重合. 这体现圆具有什么样的性质?
能够重合的两个圆叫做等圆.
注:半径相等的两个圆是等圆, 反过来,同圆或等圆的半径相等.
一个圆上两个弧重合或两个等圆上两个弧重合称之为等弧。
注: ①等弧是全等的,不仅是弧的长度相等.
②等弧只存在于同圆或等圆中.
等圆
半径相同,圆心不同.
同心圆
圆心相同,半径不同。
·
C
O
A
·
C
O1
A
·
C
O
A
3.同圆是等圆吗?
不是
“等弧”不等于“长度相等的弧”,等弧仅仅存在于同圆或等圆中.
D
C
A
B
想一想,长度相等的弧是等弧吗?
如图,AB和CD的拉直长度都是10 cm,平移并调整小圆的位置,这两条弧不可能完全重合,因为这两条弧弯曲程度不同.
(
(
等弧:在同圆或等圆中,能够互相重合的弧叫做等弧.
例1 以下命题:(1)半圆是弧,但弧不一定是半圆;(2)过圆上任意一点只能作一条弦,且这条弦是直径;(3)弦是直径;(4)直径是圆中最长的弦;(5)直径不是弦;(6)优弧大于劣弧;(7)以O为圆心可以画无数个圆. 正确的个数为( )
A.1 B.2 C.3 D.4
C
例2 如图, 在☉O 中,点 A , O , D 以及点 B , O , C 分别在
同一条直线上, 图中弦的条数为( )
A. 2 B. 3 C. 4 D.5
A
四 圆的对称性
(1)圆是轴对称图形吗?如果是,它的对称轴是什么?你能找到多少条对称轴?
(2)你是怎么得出结论的?
用折叠的方法
●O
思考
圆是轴对称图形,其对称轴是任意一条直径所在的直线,可以找到无数条对称轴.
在纸上任画一个⊙O, 并剪下来. 将⊙O 沿任意一条直径(例如直径CD) 对折, 你发现了什么?
讨论
直径CD两侧的两个半圆能完全重合
圆是轴对称图形, 任意一条直径所在的直线都是圆的对称轴.
重合,圆是中心对称图形
.
O
A
B
180°
问题1 将圆绕圆心旋转180°后,得到的图形与原图形重合吗?由此你得到什么结论呢?
探究
问题2 把圆绕圆心旋转任意一个角度呢?仍与原来的圆重合吗?
O
α
重合,圆是旋转对称图形,无论绕圆心旋转多少度,它都能与自身重合,对称中心即为其圆心.
·
1. 圆有无数条对称轴,但只有一个对称中心.
2. 因为直径是弦,弦是线段,而对称轴是直线,所以说“圆的对称轴是直径所在的直线”或说成“圆的对称轴是经过圆心的直线”.
温馨提示
为什么通常要把车轮设计成圆形? 请说说理由.
古代车轮的演变
议一议
圆形车轮转动到任何一个角度,圆心到地面的距离都不变使车轮在滚动时很平滑
例1 下列说法中正确的是( )
A. 圆的任意一条直径都是它的对称轴
B. 经过圆心的直线是圆的对称轴
C. 与圆相交的直线是圆的对称轴
D. 与半径垂直的直线是圆的对称轴
B
1.下列关于圆的说法,正确的是( )
A.在平面内圆是所有到定点距离等于定长的点的集合
B.同一平面内两个半径相等的圆必定关于某一条直线成轴对称
C.优弧大于劣弧
D.圆绕圆心旋转任意角度都与自身重合
随堂练习
ABD
2.下列说法中正确的有( )
(1)圆是轴对称图形;(2)圆是旋转对称图形;(3)圆不是中心对称图形;(4)圆是轴对称图形但不是旋转对称图形.
A.1个 B.2个
C.3个 D.4个
B
3.已知⊙O的半径为2、AB是⊙O的一条弦,则 AB的长不可能是( )
A. 2 B. 3
C.4 D.5
D
4. 已知☉O 的半径为 6 cm , P 为线段 OA 的中点,若点 P
在☉O 上,则 OA 的长( )
A. 等于 6 cm B. 等于 12 cm
C. 小于 6 cm D. 大于 12 cm
B
5.如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,E、F分别是AB、AC的中点.以点B为圆心,BC为半径画圆,判断点A、 C、E、F与⊙B的位置关系,并说明理由.
A
B
C
E
F
解:连接BF. C在⊙B上;在直角△ABC中,
AB=
则A在⊙B的外部;
BE= AB= ×5= <3=BC,则E在⊙B内部;
CP= AC= ×4=2,则在直角△BCF中,
BF= ,则F在⊙B的外部.
圆
定义
旋转定义:要画一个确定的圆,关键是确定圆心和半径
集合定义:同圆半径相等
弦:直径是圆中最长的弦
弧:劣弧、半圆、优弧.
有关概念
点在圆外 d > r.
点在圆上 d = r.
点在圆内 d < r.
点与圆的
位置关系
课堂小结
圆的对称性
圆是轴对称图形
圆是中心对称图形
