2.4过不共线三点作圆课件(共25张PPT)2023-2024学年度湘教版数学九年级下册
文档属性
| 名称 | 2.4过不共线三点作圆课件(共25张PPT)2023-2024学年度湘教版数学九年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 462.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-18 14:30:24 | ||
图片预览






文档简介
(共25张PPT)
2.4 过不共线三点作圆
九年级下
湘教版
1.探索平面内确定一个圆的条件.
2.了解不在同一直线上的三个点确定一个圆,会用尺规过不在同一直线上的三个点作圆.
3.了解三角形的外接圆,三角形外心等概念.
学习目标
重点
难点
新课引入
问题1 过几点可以确定一条直线?
两点
那么过几点可以确定一个圆呢?
问题2 过几点可以确定一个三角形?
三点
一 过不共线三点作圆
探究
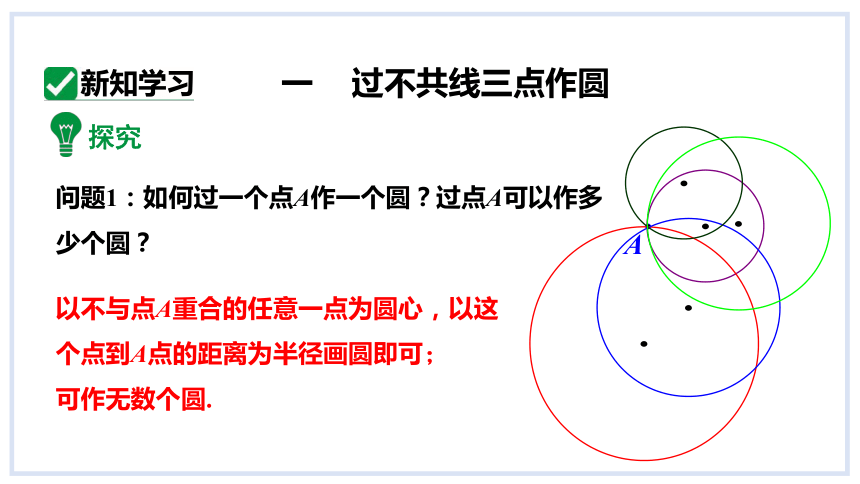
问题1:如何过一个点A作一个圆?过点A可以作多少个圆?
·
·
·
·
·
以不与点A重合的任意一点为圆心,以这个点到A点的距离为半径画圆即可;
可作无数个圆.
A
新知学习
问题2:如何过两点A、B作一个圆?可以作多少个圆?
·
·
·
·
A
B
作线段AB 的垂直平分线,以其上任意一点为圆心,以该点到点A(或B)的距离为半径画圆即可;
可作无数个圆.
分析:根据圆的性质,圆心到圆上的点的距离都等于半径,所以可得圆心在AB的垂直平分线上.
线段垂直平分线的尺规作图方法:
2.作直线MN,直线MN即为所求.
A
N
M
B
1.分别以点A和点B为圆心,以大于 AB的长为半径作弧,两弧相交于点M和点N;
问题3:如何过不在同一直线上的三点作圆?可以做多少个圆?
A
B
C
D
E
G
F
●o
经过B,C两点的圆的圆心在线段BC的垂直平分线上.
经过A,B,C三点的圆的圆心应该在这两条垂直平分线的交点O的位置.
经过A,B两点的圆的圆心在线段AB的垂直平分线上.
以点O为圆心,OA或OB或OC的距离为半径画圆,只能画一个圆.
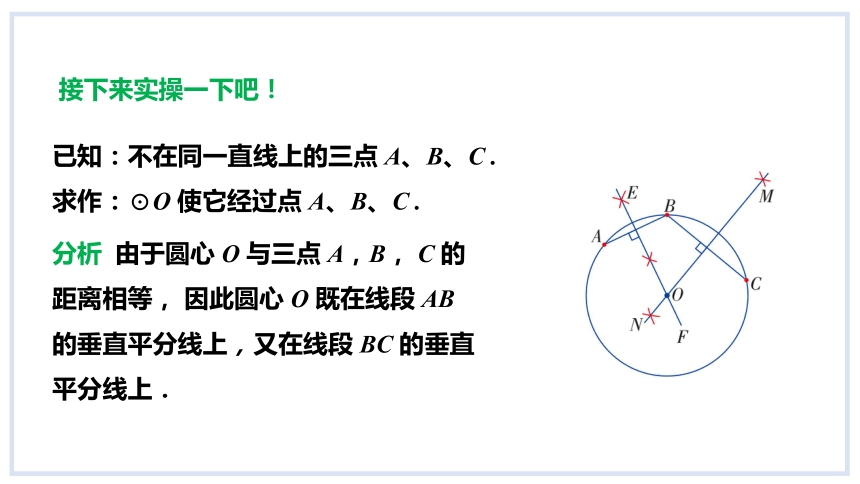
已知:不在同一直线上的三点 A、B、C .
求作:⊙O 使它经过点 A、B、C .
分析 由于圆心 O 与三点 A,B, C 的距离相等, 因此圆心 O 既在线段 AB 的垂直平分线上,又在线段 BC 的垂直平分线上.
接下来实操一下吧!
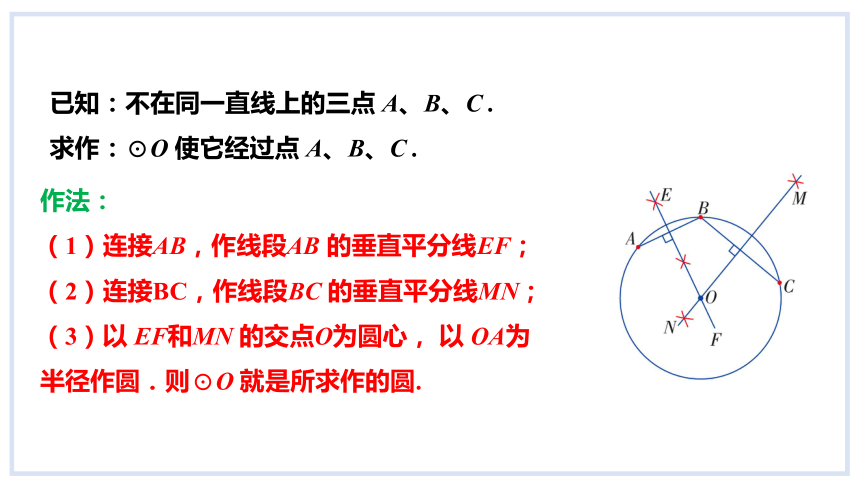
已知:不在同一直线上的三点 A、B、C .
求作:⊙O 使它经过点 A、B、C .
作法:
(1)连接AB,作线段AB 的垂直平分线EF;
(2)连接BC,作线段BC 的垂直平分线MN;
(3)以 EF和MN 的交点O为圆心, 以 OA为半径作圆.则⊙O 就是所求作的圆.
证明:假设过同一直线上的三点可以作圆.
则该圆的圆心到 A、B、C 三点的距离都相等,
即圆心是线段 AB、BC 垂直平分线的交点.
分别作 AB、BC 垂直平分线l1、l2.
显然 l1∥l2,
L1 与 l2 无交点,故产生矛盾.
所以假设不成立.
即过同一直线上的三点不能作圆.
问题4:过在同一直线上的三点 A,B,C 可以作一个圆吗?
归纳
先假设命题的结论不成立,由此经过推理得出矛盾 (常与公理、定理、定义或已知条件相矛盾),由矛盾判定假设不正确,从而得到原命题成立,这种方法叫做反证法.
1.假设命题的结论不成立;2.从这个假设出发,经过推理,得出矛盾;
3.由矛盾判定假设不正确,从而肯定命题的结论正确
反证法的定义
反证法的一般步骤
思考
经过四个点能否作圆?
1、
A
B
C
D
2、
A
B
C
D
所以经过四点不一定能作圆!
4、
A
B
C
A
B
C
D
3、
B
A
C
D
D
归纳
经过不在同一直线上的三点可以作一个圆而且只能作一个圆.
例1 已知:不在同一直线上的三点 A、B、C.
求作: ⊙O,使它经过点 A、B、C.
作法:1、连接 AB,作线段 AB 的垂直平分线 MN;
2、连接 AC,作线段 AC 的垂直平分线 EF,交 MN 于点O;
3、以 O 为圆心,OB 为半径作圆.
所以⊙O就是所求作的圆.
O
N
M
F
E
A
B
C
经过三角形的三个顶点能作一个圆吗?为什么?
由于△ABC 的顶点不在同一直线上,因此过这三个
顶点可以作一个圆,并且只可以作一个圆.
二 三角形的外接圆及外心
思考
1. 外接圆
经过三角形的三个顶点可以做一个圆,这个圆叫做三角形的外接圆.如:
⊙O 叫做△ABC 的________,
△ABC 叫做⊙O 的____________.
2. 三角形的外心
定义:
外接圆
内接三角形
三角形外接圆的圆心叫做三角形的外心.
作图:
三角形三边垂直平分线的交点.
到三角形三个顶点的距离相等.
性质:
A
B
C
O
●
例1 分别做锐角三角形,直角三角形,钝角三角形的外接圆.
锐角三角形的外心位于三角形内;
直角三角形的外心位于直角三角形斜边的中点;
钝角三角形的外心位于三角形外.
总结:
例2 任意画一个三角形,作这个三角形的外接圆.
如图所示,分别作△ABC 中AC , BC 边的垂直平分线, 其交点为O, 连OA , 则以点O 为圆心, AO长为半径的圆是△ABC 的外接圆.
随堂练习
1. △ABC 是锐角三角形,它的外心 O 在三角形的内部. 如果△ABC 是钝角三角形,外心 O 在三角形的什么位置? 如果△ABC 是直角三角形,外心 O 在△ABC 的什么位置? 分别画出它们的外接圆, 并给予判断.
2. 如图, △ABC 内接于☉O, ∠B =30°, AC = 3 cm,
则 ☉O 的半径长为______cm.
3
3. 如图,直角坐标系中一条圆弧经过网格点 A、B、C,其中,B点坐标为 (4,4),则该圆弧所在圆的圆心坐标为__________.
(2,0)
4.一个等腰三角形的底边长是6,腰长是一元二次方程(x-3)(x-5)=0的一根,则此三角形的外接圆的半径是( )
A.3.2 B. C.3.5 D.4
B
5.如图,在平面直角坐标系中,点A、B、C的坐标分别为(1,4),(5,4),(1,0),则以A、B、C为顶点的三角形外接圆的圆心坐标是( )
A.(3,2) B.(2,3)
C.(1,3) D.(3,1)
A
6. 如图是一块破残的圆形玻璃镜,现要复制一块同样大小的圆形玻璃,你能画出要复制的圆形玻璃镜图吗?
三角形
外接圆
作圆
过不共线三点
作圆
1.过一点可以作无数个圆;
2.过两点可以作无数个圆;
3.不在同一直线上的三个点确定一个圆
1.经过三角形的三个顶点的圆叫做三角形的外接圆;
2.外接圆的圆心叫三角形的外心
3.三角形的外心到三角形的三个顶点的距离相等.
课堂小结
2.4 过不共线三点作圆
九年级下
湘教版
1.探索平面内确定一个圆的条件.
2.了解不在同一直线上的三个点确定一个圆,会用尺规过不在同一直线上的三个点作圆.
3.了解三角形的外接圆,三角形外心等概念.
学习目标
重点
难点
新课引入
问题1 过几点可以确定一条直线?
两点
那么过几点可以确定一个圆呢?
问题2 过几点可以确定一个三角形?
三点
一 过不共线三点作圆
探究
问题1:如何过一个点A作一个圆?过点A可以作多少个圆?
·
·
·
·
·
以不与点A重合的任意一点为圆心,以这个点到A点的距离为半径画圆即可;
可作无数个圆.
A
新知学习
问题2:如何过两点A、B作一个圆?可以作多少个圆?
·
·
·
·
A
B
作线段AB 的垂直平分线,以其上任意一点为圆心,以该点到点A(或B)的距离为半径画圆即可;
可作无数个圆.
分析:根据圆的性质,圆心到圆上的点的距离都等于半径,所以可得圆心在AB的垂直平分线上.
线段垂直平分线的尺规作图方法:
2.作直线MN,直线MN即为所求.
A
N
M
B
1.分别以点A和点B为圆心,以大于 AB的长为半径作弧,两弧相交于点M和点N;
问题3:如何过不在同一直线上的三点作圆?可以做多少个圆?
A
B
C
D
E
G
F
●o
经过B,C两点的圆的圆心在线段BC的垂直平分线上.
经过A,B,C三点的圆的圆心应该在这两条垂直平分线的交点O的位置.
经过A,B两点的圆的圆心在线段AB的垂直平分线上.
以点O为圆心,OA或OB或OC的距离为半径画圆,只能画一个圆.
已知:不在同一直线上的三点 A、B、C .
求作:⊙O 使它经过点 A、B、C .
分析 由于圆心 O 与三点 A,B, C 的距离相等, 因此圆心 O 既在线段 AB 的垂直平分线上,又在线段 BC 的垂直平分线上.
接下来实操一下吧!
已知:不在同一直线上的三点 A、B、C .
求作:⊙O 使它经过点 A、B、C .
作法:
(1)连接AB,作线段AB 的垂直平分线EF;
(2)连接BC,作线段BC 的垂直平分线MN;
(3)以 EF和MN 的交点O为圆心, 以 OA为半径作圆.则⊙O 就是所求作的圆.
证明:假设过同一直线上的三点可以作圆.
则该圆的圆心到 A、B、C 三点的距离都相等,
即圆心是线段 AB、BC 垂直平分线的交点.
分别作 AB、BC 垂直平分线l1、l2.
显然 l1∥l2,
L1 与 l2 无交点,故产生矛盾.
所以假设不成立.
即过同一直线上的三点不能作圆.
问题4:过在同一直线上的三点 A,B,C 可以作一个圆吗?
归纳
先假设命题的结论不成立,由此经过推理得出矛盾 (常与公理、定理、定义或已知条件相矛盾),由矛盾判定假设不正确,从而得到原命题成立,这种方法叫做反证法.
1.假设命题的结论不成立;2.从这个假设出发,经过推理,得出矛盾;
3.由矛盾判定假设不正确,从而肯定命题的结论正确
反证法的定义
反证法的一般步骤
思考
经过四个点能否作圆?
1、
A
B
C
D
2、
A
B
C
D
所以经过四点不一定能作圆!
4、
A
B
C
A
B
C
D
3、
B
A
C
D
D
归纳
经过不在同一直线上的三点可以作一个圆而且只能作一个圆.
例1 已知:不在同一直线上的三点 A、B、C.
求作: ⊙O,使它经过点 A、B、C.
作法:1、连接 AB,作线段 AB 的垂直平分线 MN;
2、连接 AC,作线段 AC 的垂直平分线 EF,交 MN 于点O;
3、以 O 为圆心,OB 为半径作圆.
所以⊙O就是所求作的圆.
O
N
M
F
E
A
B
C
经过三角形的三个顶点能作一个圆吗?为什么?
由于△ABC 的顶点不在同一直线上,因此过这三个
顶点可以作一个圆,并且只可以作一个圆.
二 三角形的外接圆及外心
思考
1. 外接圆
经过三角形的三个顶点可以做一个圆,这个圆叫做三角形的外接圆.如:
⊙O 叫做△ABC 的________,
△ABC 叫做⊙O 的____________.
2. 三角形的外心
定义:
外接圆
内接三角形
三角形外接圆的圆心叫做三角形的外心.
作图:
三角形三边垂直平分线的交点.
到三角形三个顶点的距离相等.
性质:
A
B
C
O
●
例1 分别做锐角三角形,直角三角形,钝角三角形的外接圆.
锐角三角形的外心位于三角形内;
直角三角形的外心位于直角三角形斜边的中点;
钝角三角形的外心位于三角形外.
总结:
例2 任意画一个三角形,作这个三角形的外接圆.
如图所示,分别作△ABC 中AC , BC 边的垂直平分线, 其交点为O, 连OA , 则以点O 为圆心, AO长为半径的圆是△ABC 的外接圆.
随堂练习
1. △ABC 是锐角三角形,它的外心 O 在三角形的内部. 如果△ABC 是钝角三角形,外心 O 在三角形的什么位置? 如果△ABC 是直角三角形,外心 O 在△ABC 的什么位置? 分别画出它们的外接圆, 并给予判断.
2. 如图, △ABC 内接于☉O, ∠B =30°, AC = 3 cm,
则 ☉O 的半径长为______cm.
3
3. 如图,直角坐标系中一条圆弧经过网格点 A、B、C,其中,B点坐标为 (4,4),则该圆弧所在圆的圆心坐标为__________.
(2,0)
4.一个等腰三角形的底边长是6,腰长是一元二次方程(x-3)(x-5)=0的一根,则此三角形的外接圆的半径是( )
A.3.2 B. C.3.5 D.4
B
5.如图,在平面直角坐标系中,点A、B、C的坐标分别为(1,4),(5,4),(1,0),则以A、B、C为顶点的三角形外接圆的圆心坐标是( )
A.(3,2) B.(2,3)
C.(1,3) D.(3,1)
A
6. 如图是一块破残的圆形玻璃镜,现要复制一块同样大小的圆形玻璃,你能画出要复制的圆形玻璃镜图吗?
三角形
外接圆
作圆
过不共线三点
作圆
1.过一点可以作无数个圆;
2.过两点可以作无数个圆;
3.不在同一直线上的三个点确定一个圆
1.经过三角形的三个顶点的圆叫做三角形的外接圆;
2.外接圆的圆心叫三角形的外心
3.三角形的外心到三角形的三个顶点的距离相等.
课堂小结
