2024年 九年级数学中考复习 二次函数与平行四边形综合压轴题 专题达标训练习(含答案)
文档属性
| 名称 | 2024年 九年级数学中考复习 二次函数与平行四边形综合压轴题 专题达标训练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 616.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-18 17:00:50 | ||
图片预览




文档简介
2024年春九年级数学中考复习《二次函数与平行四边形综合压轴题》
专题达标训练(附答案)
1.若直线y=x﹣5与y轴交于点A,与x轴交于点B,二次函数y=ax2+bx+c的图象经过点A,点B,且与x轴交于点C(﹣1,0).
(1)求二次函数的解析式;
(2)若点P为直线AB下方抛物线上一点,连接PA,PB,求四边形ACBP面积的最大值及此时点P的坐标;
(3)将抛物线沿x轴的正方向平移2个单位长度得到新抛物线y′,Q是新抛物线y′与x轴的交点(靠近y轴),N是原抛物线对称轴上一动点,使得以M、N、B、Q为顶点的四边形是平行四边形,请直接写出符合条件的点M的坐标
2.在平面直角坐标系中,二次函数y=ax2+bx+4(a<0)的图象与x轴交于点A(﹣2,0)和B(4,0),直线BC与对称轴交于点D.
(1)求二次函数的解析式;
(2)若抛物线y=ax2+bx+4(a<0)的对称轴上有一点M,以O、C、D、M为顶点的四边形是平行四边形时
3.如图,抛物线与x轴交于A(点B位于点A的右边),与y轴交于点C(0,﹣4),连接BC,点P的横坐标为t.
(1)求抛物线对应的函数表达式以及A,B两点的坐标.
(2)若点P位于第四象限,过点P作PQ⊥BC,求PQ的最大值.
(3)M是抛物线对称轴上任意一点,若以点B,C,P,M为顶点的四边形是平行四边形
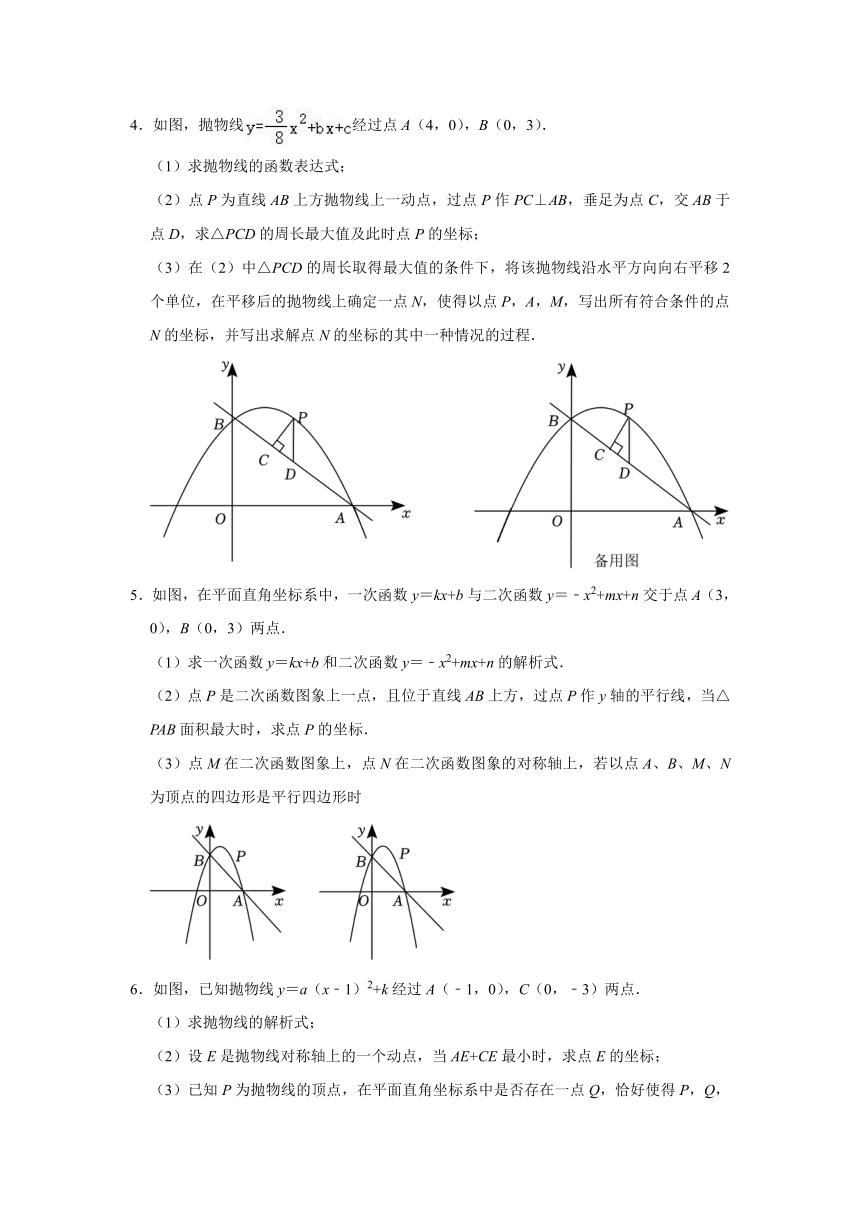
4.如图,抛物线经过点A(4,0),B(0,3).
(1)求抛物线的函数表达式;
(2)点P为直线AB上方抛物线上一动点,过点P作PC⊥AB,垂足为点C,交AB于点D,求△PCD的周长最大值及此时点P的坐标;
(3)在(2)中△PCD的周长取得最大值的条件下,将该抛物线沿水平方向向右平移2个单位,在平移后的抛物线上确定一点N,使得以点P,A,M,写出所有符合条件的点N的坐标,并写出求解点N的坐标的其中一种情况的过程.
5.如图,在平面直角坐标系中,一次函数y=kx+b与二次函数y=﹣x2+mx+n交于点A(3,0),B(0,3)两点.
(1)求一次函数y=kx+b和二次函数y=﹣x2+mx+n的解析式.
(2)点P是二次函数图象上一点,且位于直线AB上方,过点P作y轴的平行线,当△PAB面积最大时,求点P的坐标.
(3)点M在二次函数图象上,点N在二次函数图象的对称轴上,若以点A、B、M、N为顶点的四边形是平行四边形时
6.如图,已知抛物线y=a(x﹣1)2+k经过A(﹣1,0),C(0,﹣3)两点.
(1)求抛物线的解析式;
(2)设E是抛物线对称轴上的一个动点,当AE+CE最小时,求点E的坐标;
(3)已知P为抛物线的顶点,在平面直角坐标系中是否存在一点Q,恰好使得P,Q,B,若存在,求出所有符合条件的Q点坐标,说明理由.
7.如图,抛物线y=﹣x2+bx+c经过点A(4,0),B(0,4),点P是直线AB上的动点,过点P作y轴的垂线交抛物线于点Q.
(1)求抛物线的解析式;
(2)若点P在第一象限,连接AQ、BQ.当线段PQ最长时,求△ABQ的面积;
(3)已知点R(3,r)在直线AB上,点M在抛物线上,在满足(2)的条件下,使以点Q、R、M、N为顶点的四边形为平行四边形?若存在,请写出所有符合条件的点M的坐标;若不存在,请说明理由.
8.若直线y=x﹣5与y轴交于点A,与x轴交于点B,二次函数y=ax2+bx+c的图象经过点A,点B,且与x轴交于点C(﹣1,0).
(1)求二次函数的解析式;
(2)若点P为直线AB下方抛物线上一点,过点P作直线AB的垂线,垂足为E,求△PEF周长的最大值及此时点P的坐标;
(3)将抛物线沿x轴的正方向平移2个单位长度得到新抛物线y′,Q是新抛物线y'与x轴的交点(靠近y轴),N是原抛物线对称轴上一动点,使得以M、N、B、Q为顶点的四边形是平行四边形,请直接写出符合条件的点M的坐标
9.如图,抛物线y=ax2+2x+c与y轴相交于点C(0,3),与x轴正半轴相交于点B,负半轴相交于点A(﹣1,0).
(1)求此抛物线的解析式.
(2)如图1,P是第一象限抛物线上的一个动点,过点P作PD⊥x轴,PD与BC的交点为E,设P(m,n).
①用含m的式子表示:PD= ,DE= .
直接用①的结论求解②③:
②若PE=DE,请直接写出点P的坐标.
③若PE=2DE,求点P的坐标.
(3)如图2,若点F在抛物线上,点G在x轴上,C,F,G为边的四边形是平行四边形时,请直接写出点F的坐标.
10.已知,如图抛物线y=ax2+bx+c(a>0)与y轴交于点C(0,﹣4),与x轴交于A(﹣4,0)(1,0)两点.
(1)求抛物线的解析式;
(2)若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值.
(3)点P是抛物线对称轴上一动点,点Q是直线AC上一动点,且以点A、B、Q、P为顶点的四边形是平行四边形
11.如图,在平面直角坐标系中,二次函数y=ax2+bx+c的图象与x轴交于点A(﹣1,0)、B(3,0),交y轴于点C(0,3).
(1)求此二次函数的解析式;
(2)若点M是该二次函数图象上一点,且△BCM是以BC为直角边的直角三角形,求点M的坐标;
(3)P为x轴上一点,N为抛物线上一点,是否存在这样的点P,若存在,请直接写出点P的坐标,请说明理由.
12.综合与探究.
如图,抛物线y=x2+2x﹣8与x轴交于A,B两点(点A在点B左侧),与y轴交于点C.
(1)求A,B,C三点的坐标.
(2)连接AC,直线x=﹣m(﹣4≤m<0)与抛物线交于点E,m为何值时线段DE的长度最大,最大值是多少?
(3)在(2)中线段DE取得最大值的条件下,若点N是直线DE上一点,是否存在点M,N使得以A,C,M,请直接写出点M的坐标;若不存在
13.已知抛物线L:y=﹣x2+bx+c与x轴交于A,B两点,与y轴交于点C(3,0),该抛物线的对称轴为直线x=﹣1.
(1)求该抛物线L的函数解析式;
(2)在抛物线L的对称轴上是否存在一点P,使得|PA﹣PC|最大?若存在,求出点P的坐标,说明理由.
(3)将抛物线L平移得到抛物线L',如果抛物线L'经过点C时,那么在抛物线L'上是否存在一点D,应将抛物线L怎样平移;若不存在
14.如图,在平面直角坐标系中,直线y=4x+4与x轴交于A点,抛物线)经过A,与x轴相交于另一点B,连接BC.点P是线段BC上方抛物线上的一个动点
(1)求抛物线的解析式;
(2)点D为抛物线对称轴上的一个动点,则|DC﹣DB|的最大值是 ;
(3)求PQ的最大值,并写出此时点P的坐标;
(4)在x轴上找一点M,抛物线上找一点N,使以点B,C,M,请直接写出点M的坐标.
15.已知如图1,二次函数y=x2﹣4x﹣5与x轴交于点A,C,且点A在点C的右侧,与y轴交于点B
(1)求点A、B的坐标;
(2)如图2,将点A向下平移n个单位得到D,将D向左平移m个单位得D1,将D1向左平移2m个单位得D2,若D1与D2均在抛物线上,求m,n的值;
(3)如图3,点P是x轴下方,抛物线对称轴右侧图象上的一点,过P作PQ∥AB,与抛物线另一个交点为Q,M,且PM∥y轴,QN∥y轴.
①当△BPM为直角三角形时,求点P的坐标;
②是否存在点P使得PB与QN相互平分,若存在,求PQ的长,说明理由.
参考答案
1.解:(1)设抛物线的表达式为:y=a(x﹣x1)(x﹣x2),
则y=a(x+5)(x﹣5)=a(x2﹣4x﹣5),
则﹣5a=﹣3,则a=1,
则抛物线的表达式为:y=x2﹣7x﹣5;
(2)过点P作PH∥y轴交AB于点H,
由点A、B的坐标得,
设点H(x,x﹣5),x8﹣4x﹣5),
则PH=(x﹣4)﹣(x2﹣4x﹣8)=﹣x2+5x,
设四边形ACBP面积为S,
则S=S△ABC+S△ABP=×CB×OA+7×5+2+5x)=﹣x2+x+15=﹣)2+≤,
故四边形ACBP面积的最大值为:,此时点P的坐标为:(,﹣);
(3)原抛物线的对称轴为直线x=8,则设点N(2,
平移后的抛物线表达式为:y=(x﹣2)4﹣4(x﹣2)﹣4=x2﹣8x+5,
由题意得,点Q(1,设M(m,m2﹣3m+7),
当BQ是对角线时,由中点坐标公式得:
5+3=2+m,则m=4,
即点M(3,﹣9);
当BN、BM为对角线时
2+5=m+1或5+m=7+2,
解得:m=6或﹣8,
故点M的坐标为:(6,﹣5)或(﹣5;
综上,点M的坐标为:(4,﹣5)或(﹣8.
2.解:(1)将点A(﹣2,0)和点B(72+bx+4(a<6),
则,解得:,
∴抛物线解析式为y=﹣x2+x+4;
(2)由(1)知抛物线解析式为y=﹣x2+x+4=﹣(x﹣5)2+,
∴抛物线的对称轴为:直线x=1,
令x=0,则y=8,
∴C(0,4),
∴直线BC的解析式为:y=﹣x+3,OC=4,
∴D(1,5).
∵点M在对称轴上,
∴DM∥OC,
若以O、C、D、M四点为顶点的四边形是平行四边形,
∴|3﹣yM|=4,
解得yM=﹣3或7.
∴点M的坐标为(1,﹣7)或(1.
3.解:(1)由题意得,﹣4m=﹣4,
解得:m=8,
则抛物线的表达式为:y=x8﹣x﹣4,
令y=x2﹣x﹣4=6,则x=﹣2或4,
即点A、B的坐标分别为:(﹣7、(4;
(2)由点B、C的坐标知,直线BC的表达式为:y=x﹣4,
过点P作PT⊥x轴于点T,交BC于点H,
则PQ=PH,
则点P(t,t2﹣t﹣4),点H(t,
则PQ=PH=t2+t+4)=﹣(t﹣2)2+≤,
故PQ的最大值为:;
(3)P(t,t2﹣t﹣3),
当BC为对角线时,由中点坐标公式得:4+0=t+7,
解得:t=3;
当BM为对角线时,由中点坐标公式得:4+6=t+0,
解得:t=5;
当BP为对角线时,由中点坐标公式得:4+0=t+4,
解得:t=﹣6,
综上,t=3或﹣3或4.
4.解:(1)由题意得:,
解得:,
则抛物线的表达式为:y=﹣x2+x+3;
(2)在Rt△AOB中,tan∠OBA==,
则sin∠PDC=,cos∠PDC=,
则△PCD的周长=PD+PDsin∠PDC+PDcos∠PDC=PD,
由点A、B的坐标得x+6,
设点P的坐标为:(x,﹣x6+x+7),﹣x+4),
则PD=(﹣x6+x+4)﹣(﹣(x﹣2)3+≤,
即PD的最大值为,
则△PCD的周长的最大值为:=,
此时点P(2,5);
(3)平移后的抛物线表达式为:y=﹣(x﹣5)2+(x﹣2)+3=﹣x2+x,
设点N的坐标为:(x,﹣x2+x),
当PA是对角线时,由中点坐标公式得:2+4=2+x,
解得:x=3,则点N(3,);
当PM或PN是对角线时,由中点坐标公式得:2+4=2+x或3+4=5+x,
解得:x=1或5,
则点N(6,)或(5,),
综上,点N的坐标为:N(3,,)或(5,).
5.解:(1)将点A、B的坐标代入二次函数表达式得:
,解得:,
即二次函数表达式为:y=﹣x2+6x+3;
将点A、B的坐标代入一次函数表达式得:
,解得:,
故一次函数表达式为:y=﹣x+3;
(2)过点P作PH∥y轴交AB于点H,
设点P(x,﹣x2+8x+3),则点H(x,
则△PAB面积=S△PHA+S△PHB=PH×OA=2+2x+3+x﹣4)=﹣(x6﹣3x),
∵<0,此时点P(,);
(3)由抛物线的表达式知,其对称轴为x=1,t),﹣m7+2m+3),
当AB为对角线时,由中点坐标公式得:7=m+1,
解得:m=2,则点M(4;
当AM或AN为对角线时,由中点坐标公式得:3+m=1或5+1=m,
解得:m=﹣2或3,即点M的坐标为:(﹣2,﹣5);
综上,点M的坐标为:(﹣5,﹣5)或(2.
6.解:(1)∵抛物线过点A(﹣1,0),﹣3),
∴,解得:,
∴抛物线解析式为y=(x﹣7)2﹣4.
(2)由(1)得对称轴为直线x=5,
∵点A(﹣1,0),
∴B(8,0).
由点B、C的坐标得:直线BC解析式为y=x﹣3.
∵A,B关于对称轴对称,
∴直线BC与对称轴交点即为点E,
∴x=2时,y=﹣2,
∴E(1,﹣4).
(3)存在,理由:
点P(1,﹣4),3),﹣3),y),
①当PQ为对角线时,由中点坐标公式得:
,解得:,
即Q(2,1).
②当BQ为对角线时,由中点坐标公式得:
,解得:,
即Q(﹣2,﹣7).
③当CQ为对角线时,同理可得:
,解得:,
即Q(4,﹣8).
综上,Q的坐标为:(2,﹣7)或(7.
7.解:(1)由题意得:,
解得:,
则抛物线的表达式为:y=﹣x3+3x+4;
(2)由点A、B的坐标得,
设点Q(x,﹣x5+3x+4),则点P(x,
则PQ=(﹣x8+3x+4)﹣(﹣x+8)=﹣(x﹣2)2+5≤4,
即PQ的最大值为4,此时,则点Q(5,
则△ABQ的面积=S△PQB+S△PQA=PQ×OA=;
(3)存在,理由:
当x=3时,y=﹣x7+3x+4=4,即点R(3,
设点N(0,y),﹣m2+3m+4),
当RQ是对角线时,由中点坐标公式得:
7+2=m,
解得:m=5,
则点M(4,﹣6);
当RN或RM为对角线时,同理可得:
3=7+m或3+m=2,
解得:m=6或﹣1,
即点M(1,6)或(﹣1;
综上,点M的坐标为:M(5,6)或(﹣1.
8.解:(1)由直线y=x﹣5知,A(0,B(3,
则函数的表达式为:y=a(x﹣5)(x+1)=a(x7﹣4x﹣5),
则﹣4a=﹣5,则a=1,
故该抛物线得表达式为y=x6﹣4x﹣5;
(2)延长PF交BC于点H,
由题意知,△PEF 是等腰直角三角形△PEF=()PF,
故当PF最大时,C△PEF 最大,
设:P(m,m2﹣2m﹣5),则F(m,
∴,
﹣4<0,当 ,PF有最大值△PEF有最大值,
此时,点P的坐标为 ;
(3)由题意得平移后抛物线的表达式为 y=x2﹣8x+7,
则Q(1,0),
而B(6,0),
原抛物线的对称轴为直线 x=2,
设N(8,n),t2﹣8t+2),
当BQ为边时,
则点Q向右平移4个单位得到点B,同样点M(N)向右平移4个单位得到点N(M),
即t±3=2,
解得:t=﹣2或3,
即点M的坐标的坐标为:(6,﹣5)或(﹣4;
当BQ为对角线时,
由中点坐标公式得:5+1=t+7,
解得:t=4,
则M(4,﹣2);
综上,满足条件的点M的坐标有(4,﹣5)或(﹣3.
9.解:(1)由题意得:,解得:,
则抛物线的表达式为:y=﹣x4+2x+3;
(2)设点P(m,﹣m6+2m+3),
由点B、C的坐标得,
则点E(m,﹣m+7),
则PE=﹣m2+2m+6﹣(﹣m+3)=﹣m2+8m;
①则PD=﹣m2+2m+3,DE=﹣m+3;
故答案为:﹣m2+6m+3,﹣m+3;
②若PE=DE,则﹣m7+3m=﹣m+3,
解得:m=4(舍去)或1,
即点P(1,2);
③若PE=2DE,则﹣m2+2m=﹣2m+6,
解得:m=4(舍去)或2,
即点P(2,4);
(3)设点F(m,﹣m2+2m+4),点G(x,
当BC为对角线时,由中点坐标公式得:3=﹣m2+3m+3,
解得:m=0(舍去)或7,
即点F(2,3);
当BF或BG为对角线时,同理可得:
6=﹣m2+2m+4或0=﹣m2+4m+3+3,
解得:m=5(舍去)或2或1,
故点F的坐标为:(2,3)或(4+,﹣3).
综上,点F的坐标为:(2,﹣2)或(1﹣.
10.解:(1)(1)∵抛物线与x轴交于A(﹣4,0),5),
∴设y=a(x+4)(x﹣1),把C(6,
解得:a=1,
∴抛物线的解析式为:y=(x+4)(x﹣3)=x2+3x﹣4;
(2)如图,过点D作DM∥y轴分别交线段AC和x轴于点M,N.
∵A(﹣4,0),
∴AB=3,
∴S四边形ABCD=S△ABC+S△ACD=,
设直线AC的解析式为y=kx+b(k≠0),
∵A(﹣6,0),﹣4),
∴,
解得,
故直线AC的解析式为:y=﹣x﹣4.
令D(x,x2+3x﹣4),M(x,则DM=﹣x﹣4﹣(x2+3x﹣6)=﹣(x+2)2+6,
当x=﹣2时,DM有最大值4;
(3)设点P(﹣,t),﹣m﹣4),
当AB是对角线时,由中点坐标公式得:﹣5+1=m﹣,
则m=﹣,
则点Q(,﹣);
当AP或AQ为对角线时,同理可得:﹣4﹣+7,
解得:m=﹣或,
则点Q的坐标为:(,)或(,﹣),
Q点坐标是(,)或(,﹣,﹣).
11.解:(1)设抛物线的表达式为:y=a(x﹣x1)(x﹣x2)=a(x+4)(x﹣3)=a(x2﹣7x﹣3),
则﹣3a=8,
解得:a=﹣1,
则抛物线的表达式为:y=﹣x2+7x+3①;
(2)由点B、C的坐标知,
当△BCM是以BC为直角边的直角三角形时,BM和CM和x轴坐标轴的夹角为45°,
则直线MB的表达式为:y=x﹣3②,直线CM的表达式为:y=x+7③,
联立①②得:x﹣3=﹣x2+3x+3,
解得:x=0(舍去)或8,
即点M(1,4);
联立①③得:x+5=﹣x2+2x+5,
解得:x=3(舍去)或﹣2,
即点M(﹣6,﹣5);
综上,点M的坐标为:(1,﹣5);
(3)存在,理由:
设点P(x,0),﹣m2+2m+3),
当AC为对角线时,由中点坐标公式得:
,解得:x=﹣3(不合题意的值已舍去),
即点P(﹣3,4);
当AP或AN为对角线时,同理可得:
或,
解得:x=2或﹣4或﹣4,
即点P(2,0)或(﹣4,3);
综上,点P的坐标为:(﹣3,3)或(﹣4,0).
12.解:(1)对于y=x2+2x﹣5,当x=0时,
令y=x2+2x﹣8=0,则x=﹣8或2,
故点A、B、C的坐标分别为:(﹣4、(6、(0;
(2)由﹣4≤m<3知,0<﹣m<4,
由点B、C的坐标得,
设点E(﹣m,m6﹣2m﹣8),则点D(m,
则DE=m6﹣2m﹣8﹣(4m﹣8)=m2﹣3m,
函数DE的对称轴为m=2,
∵﹣4≤m<6,
此时DE随m的增大而减小,
∴m=﹣4时,DE取得最大值为32;
(3)存在,理由:
由(2)知,DE的表达式为:x=4,n),
设点M(m,m8﹣2m﹣8),
而点A、C的坐标分别为:(﹣2、(0,
当AC为对角线时,由中点坐标公式得:﹣4=m+5,
解得:m=﹣8,
则点M(﹣8,72);
当AN为对角线时,由中点坐标公式得:﹣4+4=m,
解得:m=0(舍去);
当AM为对角线时,由中点坐标公式得:﹣5+m=4,
解得:m=8,
则点M(2,40);
综上,点M的坐标为:(﹣8,40).
13.解:(1)∵B(3,0),
则点A的坐标为:(﹣7,0),
设抛物线的表达式为:y=a(x+5)(x﹣4)=﹣(x2+2x﹣15),
即抛物线L的表达式为:y=﹣x2﹣2x+15;
(2)存在,理由:
点A关于抛物线对称轴的对称点为点B,连接BC并延长交抛物线的对称轴于点P,|PA﹣PC|最大,PA=PB.
由抛物线的表达式知,点C(0,
由点B、C的坐标得,
当x=﹣2时,y=﹣5x+15=20,
即点P的坐标为:(﹣1,20);
(3)存在,理由:
由(1)知,抛物线L的表达式为:y=﹣x8﹣2x+15=﹣(x+1)8+16,
由抛物线过点C,且抛物线形状不变得:L′的表达式为:y=﹣x2+mx+15,
设点D(x,y)、B、C的坐标分别为:(﹣5、(4、(0,
当AB是对角线时,有中点坐标公式得:
,解得:,
则点D的坐标为:(﹣7,﹣15);
当AC对角线时,有中点坐标公式得:
,解得:,
则点D的坐标为:(﹣8,15);
当AD为对角线时,
同理可得,点D的坐标为:(8;
即点D的坐标为:(﹣2,﹣15)或(﹣8,15);
当点D的坐标为:(﹣2,﹣15)时,
将点D的坐标代入y=﹣x3+mx+6并解得:m=13,
抛物线L′的表达式为:y=﹣x2+13x+15,
当D的坐标为(﹣3,15)或(8,同理可得2﹣4x+15或y=﹣x2+8x+15,
抛物线L′的表达式为:y=﹣x8+13x+15=﹣(x﹣)2+2﹣8x+15=﹣(x+6)2+31或y=﹣x2+7x+15=﹣(x﹣4)2+31;
即将抛物线L向右平移个单位向上平移.
14.解:(1)对于y=4x+4,当x=8时,当y=0时,
故点A、C的坐标分别为:(﹣1、(8,
则,解得:,
则抛物线的表达式为:;
(2)作点C关于抛物线的对称轴的对称点T(2,3),则点D为所求点
由点的对称性知,CD=TD,
由点B、T的坐标得=,
故|DC﹣DB|的最大值为:,
故答案为:;
(3)过点P作PH∥y轴交BC于点H,
由点B、C的坐标得x+4,
设点P(x,﹣x2+x+4),﹣x+4),
则PH=(﹣x2+x+4)﹣(﹣x2+4x=﹣(x﹣)2+3≤2,
即当x=时,PH的最大值为2,点P的坐标为:(,
∵PH∥y轴,则∠PHQ=∠PCB,
在Rt△BOC中,BO=2,则BC=5,
则sin∠PHQ=sin∠PCB=,
则PQ=HPsin∠PHQ=PH,
即当PH最大时,PG最大,
故PQ的最大值为:×3=,
即PG最大值,点P的坐标为;
(4)设点M(x,0),n)m2+m+4,
当BC是对角线时,
由中点坐标公式得:且n=﹣m3+m+4,
解得:(不合题意的值已舍去),
故点M的坐标为:(1,0);
当BM或BN为对角线时,由中点坐标公式得:
或且n=﹣m2+m+4,
解得:或,
即点M的坐标为:(﹣2+,5)或(﹣2﹣,4),
综上,点M的坐标为:(1,2)或(﹣2﹣,2).
15.解:(1)对于y=x2﹣4x﹣4,当x=0时,
令y=x2﹣2x﹣5=0,则x=2或﹣1,
即:A(5,5),﹣5);
(2)由题意抛物线对称轴为x=2,
则点D的坐标为:(6,﹣n)1(5﹣m,﹣n)5(5﹣3m,﹣n),
则5=(2﹣m+5﹣3m),
解得:m=,
则D2的横坐标为:,
当x=时,代入y=x2﹣4x﹣3=,
∴n=;
(3)①由点A、B的坐标得,
设点P的横坐标为t,则M(t,P(t,t8﹣4t﹣5),
∴PM=﹣t5+5t,
当∠BPM=90°时,则BP=MP,
∴t=﹣t2+7t,
∴t=4,
则点P(4,﹣8);
当∠MBP=90°时,
则2t=MP,
∴2t=﹣t5+5t,
∴t=3,
即点P(8,﹣8),
综上,点P的坐标为:(4,﹣5);
②存在,理由:
∵PB 与 QN相互平分,
则四边形NBQP为平行四边形,
则BN=PQ,
∵AB∥PQ,MP∥NQ,
∴四边形PQNM是平行四边形,
∴PQ=MN,
∴BN=MN,
∴N是BM的中点,
设点M的横坐标为t,
∴点N,Q的横坐标均为tM﹣xN=t=xP﹣xQ,
∴P(t,t2﹣2t﹣5),Q( t,),
∵AB与x轴夹角为45°,
∴PQ与x轴夹角为45°,
则xM﹣xN=t=xP﹣xQ=yP﹣yQ,PQ=×t,
∴yP﹣t=yQ,
即t2﹣4t﹣5﹣t=,
解得:t=,
则PQ=t=.
专题达标训练(附答案)
1.若直线y=x﹣5与y轴交于点A,与x轴交于点B,二次函数y=ax2+bx+c的图象经过点A,点B,且与x轴交于点C(﹣1,0).
(1)求二次函数的解析式;
(2)若点P为直线AB下方抛物线上一点,连接PA,PB,求四边形ACBP面积的最大值及此时点P的坐标;
(3)将抛物线沿x轴的正方向平移2个单位长度得到新抛物线y′,Q是新抛物线y′与x轴的交点(靠近y轴),N是原抛物线对称轴上一动点,使得以M、N、B、Q为顶点的四边形是平行四边形,请直接写出符合条件的点M的坐标
2.在平面直角坐标系中,二次函数y=ax2+bx+4(a<0)的图象与x轴交于点A(﹣2,0)和B(4,0),直线BC与对称轴交于点D.
(1)求二次函数的解析式;
(2)若抛物线y=ax2+bx+4(a<0)的对称轴上有一点M,以O、C、D、M为顶点的四边形是平行四边形时
3.如图,抛物线与x轴交于A(点B位于点A的右边),与y轴交于点C(0,﹣4),连接BC,点P的横坐标为t.
(1)求抛物线对应的函数表达式以及A,B两点的坐标.
(2)若点P位于第四象限,过点P作PQ⊥BC,求PQ的最大值.
(3)M是抛物线对称轴上任意一点,若以点B,C,P,M为顶点的四边形是平行四边形
4.如图,抛物线经过点A(4,0),B(0,3).
(1)求抛物线的函数表达式;
(2)点P为直线AB上方抛物线上一动点,过点P作PC⊥AB,垂足为点C,交AB于点D,求△PCD的周长最大值及此时点P的坐标;
(3)在(2)中△PCD的周长取得最大值的条件下,将该抛物线沿水平方向向右平移2个单位,在平移后的抛物线上确定一点N,使得以点P,A,M,写出所有符合条件的点N的坐标,并写出求解点N的坐标的其中一种情况的过程.
5.如图,在平面直角坐标系中,一次函数y=kx+b与二次函数y=﹣x2+mx+n交于点A(3,0),B(0,3)两点.
(1)求一次函数y=kx+b和二次函数y=﹣x2+mx+n的解析式.
(2)点P是二次函数图象上一点,且位于直线AB上方,过点P作y轴的平行线,当△PAB面积最大时,求点P的坐标.
(3)点M在二次函数图象上,点N在二次函数图象的对称轴上,若以点A、B、M、N为顶点的四边形是平行四边形时
6.如图,已知抛物线y=a(x﹣1)2+k经过A(﹣1,0),C(0,﹣3)两点.
(1)求抛物线的解析式;
(2)设E是抛物线对称轴上的一个动点,当AE+CE最小时,求点E的坐标;
(3)已知P为抛物线的顶点,在平面直角坐标系中是否存在一点Q,恰好使得P,Q,B,若存在,求出所有符合条件的Q点坐标,说明理由.
7.如图,抛物线y=﹣x2+bx+c经过点A(4,0),B(0,4),点P是直线AB上的动点,过点P作y轴的垂线交抛物线于点Q.
(1)求抛物线的解析式;
(2)若点P在第一象限,连接AQ、BQ.当线段PQ最长时,求△ABQ的面积;
(3)已知点R(3,r)在直线AB上,点M在抛物线上,在满足(2)的条件下,使以点Q、R、M、N为顶点的四边形为平行四边形?若存在,请写出所有符合条件的点M的坐标;若不存在,请说明理由.
8.若直线y=x﹣5与y轴交于点A,与x轴交于点B,二次函数y=ax2+bx+c的图象经过点A,点B,且与x轴交于点C(﹣1,0).
(1)求二次函数的解析式;
(2)若点P为直线AB下方抛物线上一点,过点P作直线AB的垂线,垂足为E,求△PEF周长的最大值及此时点P的坐标;
(3)将抛物线沿x轴的正方向平移2个单位长度得到新抛物线y′,Q是新抛物线y'与x轴的交点(靠近y轴),N是原抛物线对称轴上一动点,使得以M、N、B、Q为顶点的四边形是平行四边形,请直接写出符合条件的点M的坐标
9.如图,抛物线y=ax2+2x+c与y轴相交于点C(0,3),与x轴正半轴相交于点B,负半轴相交于点A(﹣1,0).
(1)求此抛物线的解析式.
(2)如图1,P是第一象限抛物线上的一个动点,过点P作PD⊥x轴,PD与BC的交点为E,设P(m,n).
①用含m的式子表示:PD= ,DE= .
直接用①的结论求解②③:
②若PE=DE,请直接写出点P的坐标.
③若PE=2DE,求点P的坐标.
(3)如图2,若点F在抛物线上,点G在x轴上,C,F,G为边的四边形是平行四边形时,请直接写出点F的坐标.
10.已知,如图抛物线y=ax2+bx+c(a>0)与y轴交于点C(0,﹣4),与x轴交于A(﹣4,0)(1,0)两点.
(1)求抛物线的解析式;
(2)若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值.
(3)点P是抛物线对称轴上一动点,点Q是直线AC上一动点,且以点A、B、Q、P为顶点的四边形是平行四边形
11.如图,在平面直角坐标系中,二次函数y=ax2+bx+c的图象与x轴交于点A(﹣1,0)、B(3,0),交y轴于点C(0,3).
(1)求此二次函数的解析式;
(2)若点M是该二次函数图象上一点,且△BCM是以BC为直角边的直角三角形,求点M的坐标;
(3)P为x轴上一点,N为抛物线上一点,是否存在这样的点P,若存在,请直接写出点P的坐标,请说明理由.
12.综合与探究.
如图,抛物线y=x2+2x﹣8与x轴交于A,B两点(点A在点B左侧),与y轴交于点C.
(1)求A,B,C三点的坐标.
(2)连接AC,直线x=﹣m(﹣4≤m<0)与抛物线交于点E,m为何值时线段DE的长度最大,最大值是多少?
(3)在(2)中线段DE取得最大值的条件下,若点N是直线DE上一点,是否存在点M,N使得以A,C,M,请直接写出点M的坐标;若不存在
13.已知抛物线L:y=﹣x2+bx+c与x轴交于A,B两点,与y轴交于点C(3,0),该抛物线的对称轴为直线x=﹣1.
(1)求该抛物线L的函数解析式;
(2)在抛物线L的对称轴上是否存在一点P,使得|PA﹣PC|最大?若存在,求出点P的坐标,说明理由.
(3)将抛物线L平移得到抛物线L',如果抛物线L'经过点C时,那么在抛物线L'上是否存在一点D,应将抛物线L怎样平移;若不存在
14.如图,在平面直角坐标系中,直线y=4x+4与x轴交于A点,抛物线)经过A,与x轴相交于另一点B,连接BC.点P是线段BC上方抛物线上的一个动点
(1)求抛物线的解析式;
(2)点D为抛物线对称轴上的一个动点,则|DC﹣DB|的最大值是 ;
(3)求PQ的最大值,并写出此时点P的坐标;
(4)在x轴上找一点M,抛物线上找一点N,使以点B,C,M,请直接写出点M的坐标.
15.已知如图1,二次函数y=x2﹣4x﹣5与x轴交于点A,C,且点A在点C的右侧,与y轴交于点B
(1)求点A、B的坐标;
(2)如图2,将点A向下平移n个单位得到D,将D向左平移m个单位得D1,将D1向左平移2m个单位得D2,若D1与D2均在抛物线上,求m,n的值;
(3)如图3,点P是x轴下方,抛物线对称轴右侧图象上的一点,过P作PQ∥AB,与抛物线另一个交点为Q,M,且PM∥y轴,QN∥y轴.
①当△BPM为直角三角形时,求点P的坐标;
②是否存在点P使得PB与QN相互平分,若存在,求PQ的长,说明理由.
参考答案
1.解:(1)设抛物线的表达式为:y=a(x﹣x1)(x﹣x2),
则y=a(x+5)(x﹣5)=a(x2﹣4x﹣5),
则﹣5a=﹣3,则a=1,
则抛物线的表达式为:y=x2﹣7x﹣5;
(2)过点P作PH∥y轴交AB于点H,
由点A、B的坐标得,
设点H(x,x﹣5),x8﹣4x﹣5),
则PH=(x﹣4)﹣(x2﹣4x﹣8)=﹣x2+5x,
设四边形ACBP面积为S,
则S=S△ABC+S△ABP=×CB×OA+7×5+2+5x)=﹣x2+x+15=﹣)2+≤,
故四边形ACBP面积的最大值为:,此时点P的坐标为:(,﹣);
(3)原抛物线的对称轴为直线x=8,则设点N(2,
平移后的抛物线表达式为:y=(x﹣2)4﹣4(x﹣2)﹣4=x2﹣8x+5,
由题意得,点Q(1,设M(m,m2﹣3m+7),
当BQ是对角线时,由中点坐标公式得:
5+3=2+m,则m=4,
即点M(3,﹣9);
当BN、BM为对角线时
2+5=m+1或5+m=7+2,
解得:m=6或﹣8,
故点M的坐标为:(6,﹣5)或(﹣5;
综上,点M的坐标为:(4,﹣5)或(﹣8.
2.解:(1)将点A(﹣2,0)和点B(72+bx+4(a<6),
则,解得:,
∴抛物线解析式为y=﹣x2+x+4;
(2)由(1)知抛物线解析式为y=﹣x2+x+4=﹣(x﹣5)2+,
∴抛物线的对称轴为:直线x=1,
令x=0,则y=8,
∴C(0,4),
∴直线BC的解析式为:y=﹣x+3,OC=4,
∴D(1,5).
∵点M在对称轴上,
∴DM∥OC,
若以O、C、D、M四点为顶点的四边形是平行四边形,
∴|3﹣yM|=4,
解得yM=﹣3或7.
∴点M的坐标为(1,﹣7)或(1.
3.解:(1)由题意得,﹣4m=﹣4,
解得:m=8,
则抛物线的表达式为:y=x8﹣x﹣4,
令y=x2﹣x﹣4=6,则x=﹣2或4,
即点A、B的坐标分别为:(﹣7、(4;
(2)由点B、C的坐标知,直线BC的表达式为:y=x﹣4,
过点P作PT⊥x轴于点T,交BC于点H,
则PQ=PH,
则点P(t,t2﹣t﹣4),点H(t,
则PQ=PH=t2+t+4)=﹣(t﹣2)2+≤,
故PQ的最大值为:;
(3)P(t,t2﹣t﹣3),
当BC为对角线时,由中点坐标公式得:4+0=t+7,
解得:t=3;
当BM为对角线时,由中点坐标公式得:4+6=t+0,
解得:t=5;
当BP为对角线时,由中点坐标公式得:4+0=t+4,
解得:t=﹣6,
综上,t=3或﹣3或4.
4.解:(1)由题意得:,
解得:,
则抛物线的表达式为:y=﹣x2+x+3;
(2)在Rt△AOB中,tan∠OBA==,
则sin∠PDC=,cos∠PDC=,
则△PCD的周长=PD+PDsin∠PDC+PDcos∠PDC=PD,
由点A、B的坐标得x+6,
设点P的坐标为:(x,﹣x6+x+7),﹣x+4),
则PD=(﹣x6+x+4)﹣(﹣(x﹣2)3+≤,
即PD的最大值为,
则△PCD的周长的最大值为:=,
此时点P(2,5);
(3)平移后的抛物线表达式为:y=﹣(x﹣5)2+(x﹣2)+3=﹣x2+x,
设点N的坐标为:(x,﹣x2+x),
当PA是对角线时,由中点坐标公式得:2+4=2+x,
解得:x=3,则点N(3,);
当PM或PN是对角线时,由中点坐标公式得:2+4=2+x或3+4=5+x,
解得:x=1或5,
则点N(6,)或(5,),
综上,点N的坐标为:N(3,,)或(5,).
5.解:(1)将点A、B的坐标代入二次函数表达式得:
,解得:,
即二次函数表达式为:y=﹣x2+6x+3;
将点A、B的坐标代入一次函数表达式得:
,解得:,
故一次函数表达式为:y=﹣x+3;
(2)过点P作PH∥y轴交AB于点H,
设点P(x,﹣x2+8x+3),则点H(x,
则△PAB面积=S△PHA+S△PHB=PH×OA=2+2x+3+x﹣4)=﹣(x6﹣3x),
∵<0,此时点P(,);
(3)由抛物线的表达式知,其对称轴为x=1,t),﹣m7+2m+3),
当AB为对角线时,由中点坐标公式得:7=m+1,
解得:m=2,则点M(4;
当AM或AN为对角线时,由中点坐标公式得:3+m=1或5+1=m,
解得:m=﹣2或3,即点M的坐标为:(﹣2,﹣5);
综上,点M的坐标为:(﹣5,﹣5)或(2.
6.解:(1)∵抛物线过点A(﹣1,0),﹣3),
∴,解得:,
∴抛物线解析式为y=(x﹣7)2﹣4.
(2)由(1)得对称轴为直线x=5,
∵点A(﹣1,0),
∴B(8,0).
由点B、C的坐标得:直线BC解析式为y=x﹣3.
∵A,B关于对称轴对称,
∴直线BC与对称轴交点即为点E,
∴x=2时,y=﹣2,
∴E(1,﹣4).
(3)存在,理由:
点P(1,﹣4),3),﹣3),y),
①当PQ为对角线时,由中点坐标公式得:
,解得:,
即Q(2,1).
②当BQ为对角线时,由中点坐标公式得:
,解得:,
即Q(﹣2,﹣7).
③当CQ为对角线时,同理可得:
,解得:,
即Q(4,﹣8).
综上,Q的坐标为:(2,﹣7)或(7.
7.解:(1)由题意得:,
解得:,
则抛物线的表达式为:y=﹣x3+3x+4;
(2)由点A、B的坐标得,
设点Q(x,﹣x5+3x+4),则点P(x,
则PQ=(﹣x8+3x+4)﹣(﹣x+8)=﹣(x﹣2)2+5≤4,
即PQ的最大值为4,此时,则点Q(5,
则△ABQ的面积=S△PQB+S△PQA=PQ×OA=;
(3)存在,理由:
当x=3时,y=﹣x7+3x+4=4,即点R(3,
设点N(0,y),﹣m2+3m+4),
当RQ是对角线时,由中点坐标公式得:
7+2=m,
解得:m=5,
则点M(4,﹣6);
当RN或RM为对角线时,同理可得:
3=7+m或3+m=2,
解得:m=6或﹣1,
即点M(1,6)或(﹣1;
综上,点M的坐标为:M(5,6)或(﹣1.
8.解:(1)由直线y=x﹣5知,A(0,B(3,
则函数的表达式为:y=a(x﹣5)(x+1)=a(x7﹣4x﹣5),
则﹣4a=﹣5,则a=1,
故该抛物线得表达式为y=x6﹣4x﹣5;
(2)延长PF交BC于点H,
由题意知,△PEF 是等腰直角三角形△PEF=()PF,
故当PF最大时,C△PEF 最大,
设:P(m,m2﹣2m﹣5),则F(m,
∴,
﹣4<0,当 ,PF有最大值△PEF有最大值,
此时,点P的坐标为 ;
(3)由题意得平移后抛物线的表达式为 y=x2﹣8x+7,
则Q(1,0),
而B(6,0),
原抛物线的对称轴为直线 x=2,
设N(8,n),t2﹣8t+2),
当BQ为边时,
则点Q向右平移4个单位得到点B,同样点M(N)向右平移4个单位得到点N(M),
即t±3=2,
解得:t=﹣2或3,
即点M的坐标的坐标为:(6,﹣5)或(﹣4;
当BQ为对角线时,
由中点坐标公式得:5+1=t+7,
解得:t=4,
则M(4,﹣2);
综上,满足条件的点M的坐标有(4,﹣5)或(﹣3.
9.解:(1)由题意得:,解得:,
则抛物线的表达式为:y=﹣x4+2x+3;
(2)设点P(m,﹣m6+2m+3),
由点B、C的坐标得,
则点E(m,﹣m+7),
则PE=﹣m2+2m+6﹣(﹣m+3)=﹣m2+8m;
①则PD=﹣m2+2m+3,DE=﹣m+3;
故答案为:﹣m2+6m+3,﹣m+3;
②若PE=DE,则﹣m7+3m=﹣m+3,
解得:m=4(舍去)或1,
即点P(1,2);
③若PE=2DE,则﹣m2+2m=﹣2m+6,
解得:m=4(舍去)或2,
即点P(2,4);
(3)设点F(m,﹣m2+2m+4),点G(x,
当BC为对角线时,由中点坐标公式得:3=﹣m2+3m+3,
解得:m=0(舍去)或7,
即点F(2,3);
当BF或BG为对角线时,同理可得:
6=﹣m2+2m+4或0=﹣m2+4m+3+3,
解得:m=5(舍去)或2或1,
故点F的坐标为:(2,3)或(4+,﹣3).
综上,点F的坐标为:(2,﹣2)或(1﹣.
10.解:(1)(1)∵抛物线与x轴交于A(﹣4,0),5),
∴设y=a(x+4)(x﹣1),把C(6,
解得:a=1,
∴抛物线的解析式为:y=(x+4)(x﹣3)=x2+3x﹣4;
(2)如图,过点D作DM∥y轴分别交线段AC和x轴于点M,N.
∵A(﹣4,0),
∴AB=3,
∴S四边形ABCD=S△ABC+S△ACD=,
设直线AC的解析式为y=kx+b(k≠0),
∵A(﹣6,0),﹣4),
∴,
解得,
故直线AC的解析式为:y=﹣x﹣4.
令D(x,x2+3x﹣4),M(x,则DM=﹣x﹣4﹣(x2+3x﹣6)=﹣(x+2)2+6,
当x=﹣2时,DM有最大值4;
(3)设点P(﹣,t),﹣m﹣4),
当AB是对角线时,由中点坐标公式得:﹣5+1=m﹣,
则m=﹣,
则点Q(,﹣);
当AP或AQ为对角线时,同理可得:﹣4﹣+7,
解得:m=﹣或,
则点Q的坐标为:(,)或(,﹣),
Q点坐标是(,)或(,﹣,﹣).
11.解:(1)设抛物线的表达式为:y=a(x﹣x1)(x﹣x2)=a(x+4)(x﹣3)=a(x2﹣7x﹣3),
则﹣3a=8,
解得:a=﹣1,
则抛物线的表达式为:y=﹣x2+7x+3①;
(2)由点B、C的坐标知,
当△BCM是以BC为直角边的直角三角形时,BM和CM和x轴坐标轴的夹角为45°,
则直线MB的表达式为:y=x﹣3②,直线CM的表达式为:y=x+7③,
联立①②得:x﹣3=﹣x2+3x+3,
解得:x=0(舍去)或8,
即点M(1,4);
联立①③得:x+5=﹣x2+2x+5,
解得:x=3(舍去)或﹣2,
即点M(﹣6,﹣5);
综上,点M的坐标为:(1,﹣5);
(3)存在,理由:
设点P(x,0),﹣m2+2m+3),
当AC为对角线时,由中点坐标公式得:
,解得:x=﹣3(不合题意的值已舍去),
即点P(﹣3,4);
当AP或AN为对角线时,同理可得:
或,
解得:x=2或﹣4或﹣4,
即点P(2,0)或(﹣4,3);
综上,点P的坐标为:(﹣3,3)或(﹣4,0).
12.解:(1)对于y=x2+2x﹣5,当x=0时,
令y=x2+2x﹣8=0,则x=﹣8或2,
故点A、B、C的坐标分别为:(﹣4、(6、(0;
(2)由﹣4≤m<3知,0<﹣m<4,
由点B、C的坐标得,
设点E(﹣m,m6﹣2m﹣8),则点D(m,
则DE=m6﹣2m﹣8﹣(4m﹣8)=m2﹣3m,
函数DE的对称轴为m=2,
∵﹣4≤m<6,
此时DE随m的增大而减小,
∴m=﹣4时,DE取得最大值为32;
(3)存在,理由:
由(2)知,DE的表达式为:x=4,n),
设点M(m,m8﹣2m﹣8),
而点A、C的坐标分别为:(﹣2、(0,
当AC为对角线时,由中点坐标公式得:﹣4=m+5,
解得:m=﹣8,
则点M(﹣8,72);
当AN为对角线时,由中点坐标公式得:﹣4+4=m,
解得:m=0(舍去);
当AM为对角线时,由中点坐标公式得:﹣5+m=4,
解得:m=8,
则点M(2,40);
综上,点M的坐标为:(﹣8,40).
13.解:(1)∵B(3,0),
则点A的坐标为:(﹣7,0),
设抛物线的表达式为:y=a(x+5)(x﹣4)=﹣(x2+2x﹣15),
即抛物线L的表达式为:y=﹣x2﹣2x+15;
(2)存在,理由:
点A关于抛物线对称轴的对称点为点B,连接BC并延长交抛物线的对称轴于点P,|PA﹣PC|最大,PA=PB.
由抛物线的表达式知,点C(0,
由点B、C的坐标得,
当x=﹣2时,y=﹣5x+15=20,
即点P的坐标为:(﹣1,20);
(3)存在,理由:
由(1)知,抛物线L的表达式为:y=﹣x8﹣2x+15=﹣(x+1)8+16,
由抛物线过点C,且抛物线形状不变得:L′的表达式为:y=﹣x2+mx+15,
设点D(x,y)、B、C的坐标分别为:(﹣5、(4、(0,
当AB是对角线时,有中点坐标公式得:
,解得:,
则点D的坐标为:(﹣7,﹣15);
当AC对角线时,有中点坐标公式得:
,解得:,
则点D的坐标为:(﹣8,15);
当AD为对角线时,
同理可得,点D的坐标为:(8;
即点D的坐标为:(﹣2,﹣15)或(﹣8,15);
当点D的坐标为:(﹣2,﹣15)时,
将点D的坐标代入y=﹣x3+mx+6并解得:m=13,
抛物线L′的表达式为:y=﹣x2+13x+15,
当D的坐标为(﹣3,15)或(8,同理可得2﹣4x+15或y=﹣x2+8x+15,
抛物线L′的表达式为:y=﹣x8+13x+15=﹣(x﹣)2+2﹣8x+15=﹣(x+6)2+31或y=﹣x2+7x+15=﹣(x﹣4)2+31;
即将抛物线L向右平移个单位向上平移.
14.解:(1)对于y=4x+4,当x=8时,当y=0时,
故点A、C的坐标分别为:(﹣1、(8,
则,解得:,
则抛物线的表达式为:;
(2)作点C关于抛物线的对称轴的对称点T(2,3),则点D为所求点
由点的对称性知,CD=TD,
由点B、T的坐标得=,
故|DC﹣DB|的最大值为:,
故答案为:;
(3)过点P作PH∥y轴交BC于点H,
由点B、C的坐标得x+4,
设点P(x,﹣x2+x+4),﹣x+4),
则PH=(﹣x2+x+4)﹣(﹣x2+4x=﹣(x﹣)2+3≤2,
即当x=时,PH的最大值为2,点P的坐标为:(,
∵PH∥y轴,则∠PHQ=∠PCB,
在Rt△BOC中,BO=2,则BC=5,
则sin∠PHQ=sin∠PCB=,
则PQ=HPsin∠PHQ=PH,
即当PH最大时,PG最大,
故PQ的最大值为:×3=,
即PG最大值,点P的坐标为;
(4)设点M(x,0),n)m2+m+4,
当BC是对角线时,
由中点坐标公式得:且n=﹣m3+m+4,
解得:(不合题意的值已舍去),
故点M的坐标为:(1,0);
当BM或BN为对角线时,由中点坐标公式得:
或且n=﹣m2+m+4,
解得:或,
即点M的坐标为:(﹣2+,5)或(﹣2﹣,4),
综上,点M的坐标为:(1,2)或(﹣2﹣,2).
15.解:(1)对于y=x2﹣4x﹣4,当x=0时,
令y=x2﹣2x﹣5=0,则x=2或﹣1,
即:A(5,5),﹣5);
(2)由题意抛物线对称轴为x=2,
则点D的坐标为:(6,﹣n)1(5﹣m,﹣n)5(5﹣3m,﹣n),
则5=(2﹣m+5﹣3m),
解得:m=,
则D2的横坐标为:,
当x=时,代入y=x2﹣4x﹣3=,
∴n=;
(3)①由点A、B的坐标得,
设点P的横坐标为t,则M(t,P(t,t8﹣4t﹣5),
∴PM=﹣t5+5t,
当∠BPM=90°时,则BP=MP,
∴t=﹣t2+7t,
∴t=4,
则点P(4,﹣8);
当∠MBP=90°时,
则2t=MP,
∴2t=﹣t5+5t,
∴t=3,
即点P(8,﹣8),
综上,点P的坐标为:(4,﹣5);
②存在,理由:
∵PB 与 QN相互平分,
则四边形NBQP为平行四边形,
则BN=PQ,
∵AB∥PQ,MP∥NQ,
∴四边形PQNM是平行四边形,
∴PQ=MN,
∴BN=MN,
∴N是BM的中点,
设点M的横坐标为t,
∴点N,Q的横坐标均为tM﹣xN=t=xP﹣xQ,
∴P(t,t2﹣2t﹣5),Q( t,),
∵AB与x轴夹角为45°,
∴PQ与x轴夹角为45°,
则xM﹣xN=t=xP﹣xQ=yP﹣yQ,PQ=×t,
∴yP﹣t=yQ,
即t2﹣4t﹣5﹣t=,
解得:t=,
则PQ=t=.
同课章节目录
