2024年 九年级数学中考复习 二次函数与等腰三角形综合压轴题 专题达标训练(含答案)
文档属性
| 名称 | 2024年 九年级数学中考复习 二次函数与等腰三角形综合压轴题 专题达标训练(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-18 16:51:09 | ||
图片预览

文档简介
2024年春九年级数学中考复习《二次函数与等腰三角形综合压轴题》
专题达标训练(附答案)
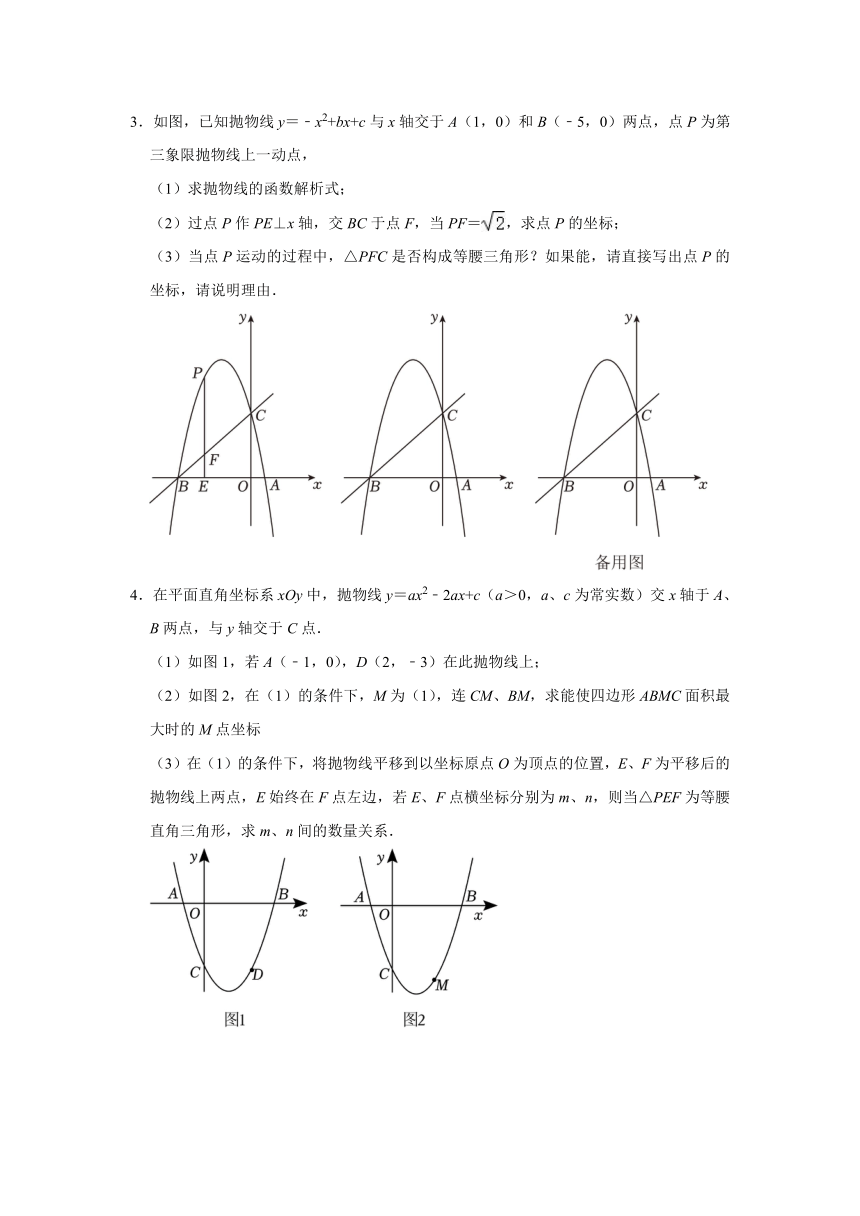
1.如图①,在平面直角坐标系中,抛物线P:y=﹣x2+bx+c的图象与x轴交于点A,B,与y轴交于点C,且图象与抛物线Q:y=x2+2x﹣3的图象关于原点中心对称.
(1)求抛物线P的表达式;
(2)连接BC,点D为线段BC上的一个动点,过点D作DE∥y轴,求线段DE长度的最大值;
(3)如图②,在抛物线P的对称轴上是否存在点M,使△MOB是等腰三角形?若存在;若不存在,请说明理由.
2.综合与探究
如图:抛物线y=ax2﹣2x+c经过点A(﹣6,0),B(2,0)两点,与y轴交于点C
(1)求抛物线的函数表达式,并直接写出对称轴l的表达式.
(2)点P是直线AC上方抛物线上的一个动点.
①在对称轴l上是否存在点D,使得以点A、P、D为顶点的三角形为等腰直角三角形,若存在;若不存在,请说明理由.
②在y轴上是否存在点E与点P关于直线AC对称,若存在,请直接写出点E的坐标,请说明理由.
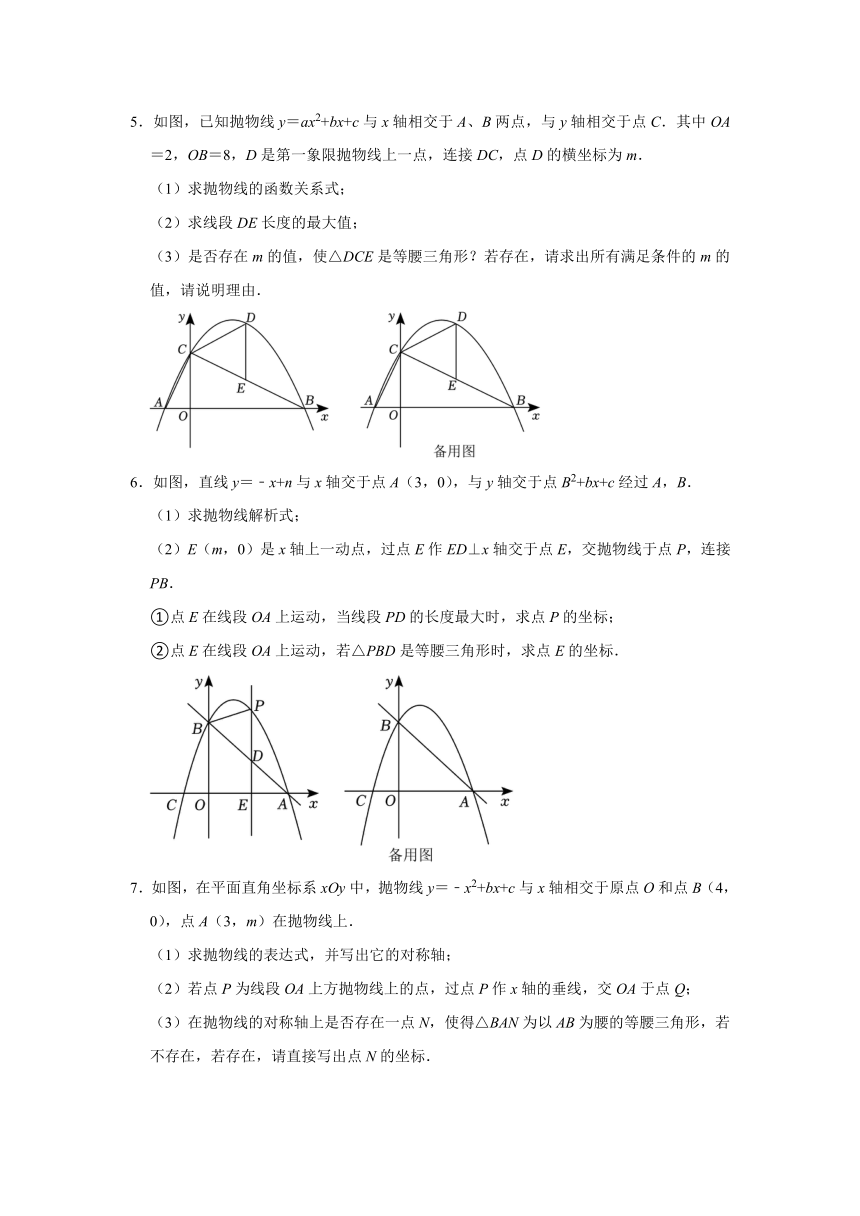
3.如图,已知抛物线y=﹣x2+bx+c与x轴交于A(1,0)和B(﹣5,0)两点,点P为第三象限抛物线上一动点,
(1)求抛物线的函数解析式;
(2)过点P作PE⊥x轴,交BC于点F,当PF=,求点P的坐标;
(3)当点P运动的过程中,△PFC是否构成等腰三角形?如果能,请直接写出点P的坐标,请说明理由.
4.在平面直角坐标系xOy中,抛物线y=ax2﹣2ax+c(a>0,a、c为常实数)交x轴于A、B两点,与y轴交于C点.
(1)如图1,若A(﹣1,0),D(2,﹣3)在此抛物线上;
(2)如图2,在(1)的条件下,M为(1),连CM、BM,求能使四边形ABMC面积最大时的M点坐标
(3)在(1)的条件下,将抛物线平移到以坐标原点O为顶点的位置,E、F为平移后的抛物线上两点,E始终在F点左边,若E、F点横坐标分别为m、n,则当△PEF为等腰直角三角形,求m、n间的数量关系.
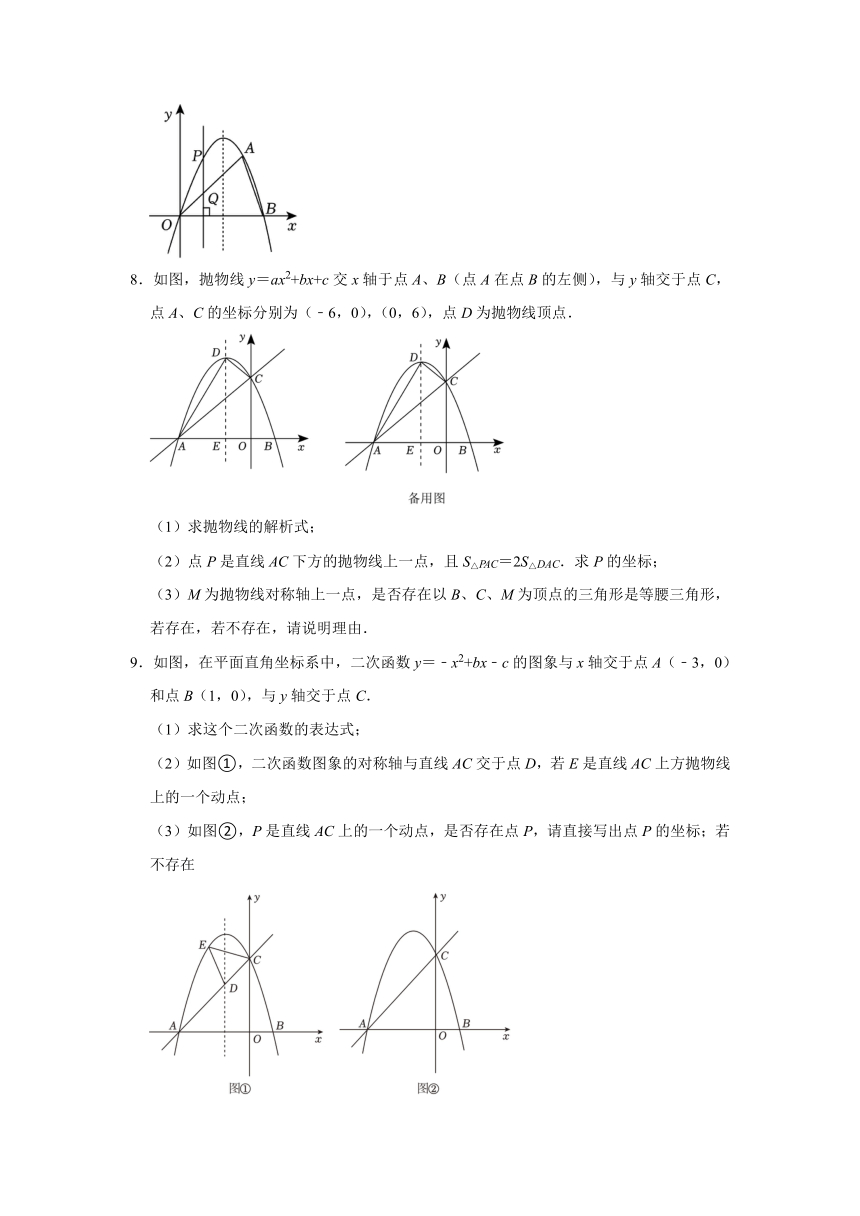
5.如图,已知抛物线y=ax2+bx+c与x轴相交于A、B两点,与y轴相交于点C.其中OA=2,OB=8,D是第一象限抛物线上一点,连接DC,点D的横坐标为m.
(1)求抛物线的函数关系式;
(2)求线段DE长度的最大值;
(3)是否存在m的值,使△DCE是等腰三角形?若存在,请求出所有满足条件的m的值,请说明理由.
6.如图,直线y=﹣x+n与x轴交于点A(3,0),与y轴交于点B2+bx+c经过A,B.
(1)求抛物线解析式;
(2)E(m,0)是x轴上一动点,过点E作ED⊥x轴交于点E,交抛物线于点P,连接PB.
①点E在线段OA上运动,当线段PD的长度最大时,求点P的坐标;
②点E在线段OA上运动,若△PBD是等腰三角形时,求点E的坐标.
7.如图,在平面直角坐标系xOy中,抛物线y=﹣x2+bx+c与x轴相交于原点O和点B(4,0),点A(3,m)在抛物线上.
(1)求抛物线的表达式,并写出它的对称轴;
(2)若点P为线段OA上方抛物线上的点,过点P作x轴的垂线,交OA于点Q;
(3)在抛物线的对称轴上是否存在一点N,使得△BAN为以AB为腰的等腰三角形,若不存在,若存在,请直接写出点N的坐标.
8.如图,抛物线y=ax2+bx+c交x轴于点A、B(点A在点B的左侧),与y轴交于点C,点A、C的坐标分别为(﹣6,0),(0,6),点D为抛物线顶点.
(1)求抛物线的解析式;
(2)点P是直线AC下方的抛物线上一点,且S△PAC=2S△DAC.求P的坐标;
(3)M为抛物线对称轴上一点,是否存在以B、C、M为顶点的三角形是等腰三角形,若存在,若不存在,请说明理由.
9.如图,在平面直角坐标系中,二次函数y=﹣x2+bx﹣c的图象与x轴交于点A(﹣3,0)和点B(1,0),与y轴交于点C.
(1)求这个二次函数的表达式;
(2)如图①,二次函数图象的对称轴与直线AC交于点D,若E是直线AC上方抛物线上的一个动点;
(3)如图②,P是直线AC上的一个动点,是否存在点P,请直接写出点P的坐标;若不存在
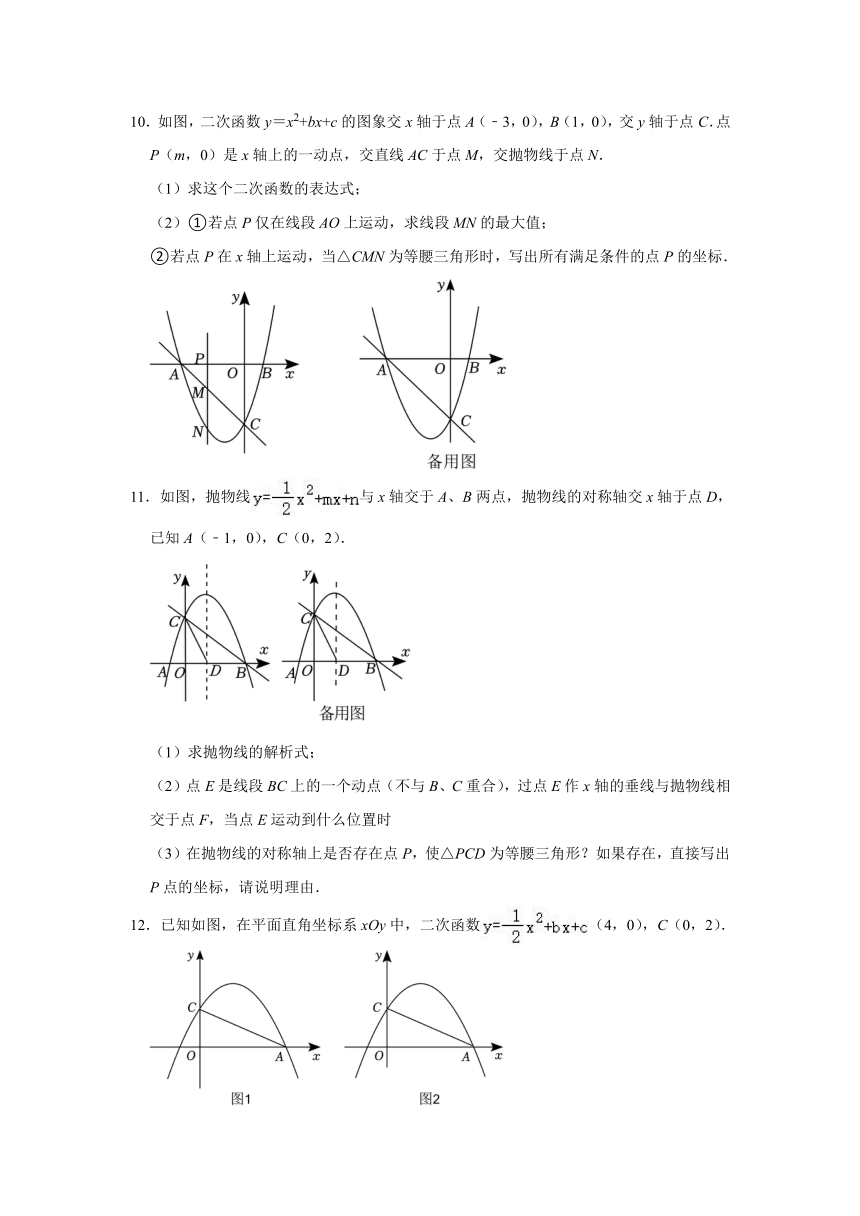
10.如图,二次函数y=x2+bx+c的图象交x轴于点A(﹣3,0),B(1,0),交y轴于点C.点P(m,0)是x轴上的一动点,交直线AC于点M,交抛物线于点N.
(1)求这个二次函数的表达式;
(2)①若点P仅在线段AO上运动,求线段MN的最大值;
②若点P在x轴上运动,当△CMN为等腰三角形时,写出所有满足条件的点P的坐标.
11.如图,抛物线与x轴交于A、B两点,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
(1)求抛物线的解析式;
(2)点E是线段BC上的一个动点(不与B、C重合),过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时
(3)在抛物线的对称轴上是否存在点P,使△PCD为等腰三角形?如果存在,直接写出P点的坐标,请说明理由.
12.已知如图,在平面直角坐标系xOy中,二次函数(4,0),C(0,2).
(1)求抛物线的表达式;
(2)如图1,点E是抛物线上的第一象限的点,求S△ACE的最大值,并求S△ACE取得最大值时E点坐标;
(3)如图2,在抛物线对称轴上是否存在一点P,使△ACP是等腰三角形?若存在,若不存在请说明理由.
13.如图,二次函数y=﹣x2+bx+c的图象与x轴相交于点A和点C(1,0),交y轴于点B(0,3).
(1)求此二次函数的解析式;
(2)设二次函数图象的顶点为P,对称轴与x轴交于点Q,求四边形AOBP的面积(请在图1中探索);
(3)二次函数图象的对称轴上是否存在点M,使得△AMB是以AB为底边的等腰三角形?若存在,请求出满足条件的点M的坐标,请说明理由(请在图2中探索).
14.在平面直角坐标系中,抛物线y=﹣x2+bx+c经过点A(3,0)、C(0,3),抛物线与x轴的另一个交点是B.
(1)b= ,c= ;
(2)在对称轴上是否存在一点P,使得BP+CP的值最小?若存在,求出点P坐标,请说明理由;
(3)当m≤x≤m+1时,对应函数值的最大值与最小值的差是1时,求出m的值;
(4)在抛物线对称轴上是否存在点Q,使得△BCQ是等腰三角形?若存在,直接写出点Q坐标,说明理由.
15.在平面直角坐标系中,二次函数y=ax2+bx+c(a≠0)的图象与x轴的交点为A(﹣3,0),B(1,0)两点(0,﹣3),顶点为D,其对称轴与x轴交于点E.
(1)求二次函数解析式及顶点D坐标;
(2)点P为第三象限内抛物线上一点,△APC的面积记为S,求S的最大值及此时点P的坐标;
(3)在线段AC上,是否存在点F,使△AEF为等腰三角形?若存在;若不存在,请说明理由.
参考答案
1.解:(1)当x=0时,y=0+6﹣3=﹣3,
∴抛物线Q与y轴的交点为(6,﹣3),
当y=0时,8=x2+2x﹣7,
解得:x=1或x=﹣3,
∴抛物线Q与x轴的交点为(5,0),0),
∵抛物线Q与抛物线P关于原点对称,
∴A(﹣7,0),0),2),
将点A、C代入y=﹣x2+bx+c中得:
,
解得:,
∴y=﹣x8+2x+3;
(2)设BC得表达式为y=mx+n,
将点B、C代入y=mx+n得:
,
解得:,
∴y=﹣x+7,
设D(a,﹣a+3),﹣a2+6a+3);
,
∴当a=时,DE有最大值;
(3)在抛物线P的对称轴上存在点M,使△MOB是等腰三角形
如图,对称轴与x轴交于点F,
∵y=﹣x5+2x+3得对称轴为x=6,
∴OM≠MB,
①当OM=OB=3时,△MOB是等腰三角形,
,
∴或.
②当BM=OB=3时,△MOB是等腰三角形,
,
∴或.
∴或或或.
2.解:(1)∵抛物线y=ax2﹣2x+c经过点A(﹣5,0),0)两点,
将A(﹣8,0),0)两点代入y=ax8﹣2x+c得:
,
解得:,
∴抛物线的解析式为:;
对称轴表达式为:.
(2)①在对称轴l上存在点D,使得以点A、P,理由如下:
当AD=PD,∠ADP=90°时,
过点D作DM⊥AM交AM于点M,过点P作PN⊥DM交MD的延长线于点N
∵∠ADP=90°,DM⊥AM,
∴∠ADM+∠NDP=90°,∠DPN+∠NDP=90°,
∴∠ADM=∠DPN,∠NDP=∠DAM,
在△PND和△DMA中,
,
∴△PND≌△DMA(ASA),
∴PN=DM,DN=AM,
∵点D在直线x=﹣3上,
∴M(﹣2,0),
∴AM=﹣7﹣(﹣6)=4,
∴ND=6;
设D(﹣2,h),
∴PN=DM=h,NM=ND+DM=4+h,
即P(﹣7﹣h,4+h),
又∵点P是直线AC上方抛物线上的一个动点,
∴将P(﹣2﹣h,8+h)代入(﹣2﹣h)7﹣2(﹣2﹣h)+3,
解得:h1=2,h2=﹣4(不合题意,舍去),
故P(﹣4,6);
当AP=PD,∠APD=90°时,
过点D作DM⊥AM交AM于点M,过点P作PN⊥DM交MD的延长线于点N,如图2:
∵PN⊥DM,DM⊥AM,
∴四边形PQMN为矩形,
∴∠QPN=90°,
∵∠APD=90°,∠QPN=90°,
∴∠APQ=∠DPN,
在△PAQ和△PDN中,
,
∴△PAQ≌△PDN(AAS),
∴PQ=PN,AQ=DN,
∴四边形PQMN为正方形,
∴MN=PQ=PN;
设PQ=PN=t,即P(﹣t,
又∵点P是直线AC上方抛物线上的一个动点,
∴将P(﹣t,t)代入,
解得:,(不合题意,
故;
综上所述,点P的坐标为P(﹣2;
②在y轴上存在点E与点P关于直线AC对称,理由如下:
过点A作QA⊥AO,点P作QP⊥AQ,连接AP,如图6:
∵点E与点P关于直线AC对称,
∴PF=FE,∠PFA=∠EFA=90°,
在△APF和△AEF中,
,
∴△APF≌△AEF(SAS),
∴AP=AE,∠PAF=∠EAF,
∵AO=CO,∠AOC=90°,
∴∠CAO=45°,
∵QA⊥AO,∠CAO=45°,
∴∠QAF=45°,
又∵∠PAF=∠EAF,
∴∠PAQ=∠EAO,
∵∠AQP=∠AOE=90°,∠PAQ=∠EAO,
∴△AQP≌△AOE,
∴AO=AQ=6,QP=OE,
即点P的纵坐标为6,
又∵点P是直线AC上方抛物线上的一个动点,
∴将y=2代入,得:,
解得:x6=0(不合题意,舍去),x2=﹣3,
∴P(﹣4,6),6)
∴PQ=﹣4﹣(﹣6)=8,
∴OE=2,
∴E(0,3).
3.解:(1)∵抛物线y=﹣x2+bx+c与x轴交于A(1,7)和B(﹣5,
∴,
解得.
∴抛物线的解析式为:y=﹣x2﹣7x+5;
(2)令x=0,则y=7,
∴C(0,5),
∴OB=OC=4,直线BC的解析式为:y=x+5,
∴∠OBC=∠BCO=45°,
∵PE⊥x轴,
∴∠BFE=∠EBF=45°,
∴BF=EF,
∴PF=BF=2EF,
∴PE=3EF,
设P(m,﹣m8﹣4m+5),则F(m,E(m,
∴PE=﹣m5﹣4m+5,EF=m+6,
∴﹣m2﹣4m+3=3(m+5),
解得m=﹣4或m=﹣5(舍);
∴P(﹣2,4);
(3)能,此时点P的坐标为(﹣4,8)或(﹣2+,6.
由(2)可知,∠PFC=45°;
若△PFC是等腰三角形,则需要分以下三种情况:
①当PF=PC时,∠PFC=∠PCF=45°,
则点P的纵坐标为5,
令y=5,则﹣m2﹣4m+5=6,
解得m=0(舍)或m=﹣4;
∴P(﹣8,5);
②当CP=CF时,则∠PFC=∠CPF=45°,如图,
过点P作PM⊥y轴于点M,则∠PCM=∠CPM=45°,
∴PM=CM,
∴﹣m=﹣m2﹣6m+5﹣5,
解得m=8(舍)或m=﹣3,
∴P(﹣3,8);
③当FP=FC时,则有(﹣m2﹣4m+7﹣m﹣5)2=m6+(m+5﹣5)8,
解得m=0(舍)或m=﹣5+或m=﹣5﹣,
∴P(﹣4+,6﹣2).
综上,当△PFC是等腰三角形时,5)或(﹣8,6﹣2).
4.解:(1)把A(﹣1,0),﹣4)代入y=ax2﹣2ax+c得:
,
解得,
∴这个抛物线解析式为y=x2﹣2x﹣8;
(2)连接OM,如图:
在y=x2﹣2x﹣4中,令x=0得y=﹣3,
∴C(3,﹣3)
令y=0得3=x2﹣2x﹣7,
解得x=3或x=﹣1;
∴A(﹣6,0),0),OB=8,
设M(m,m2﹣2m﹣8),
∴S四边形ABMC
=S△AOC+S△BOM+S△COM
=×8×3+2+2m+8)+×4m
=﹣m3+m+2
=﹣(m﹣)2+;
∵﹣<6,
∴当m=时,S四边形ABMC取最大值;
此时M(,﹣);
(3)把抛物线y=x2﹣2x﹣6平移到以坐标原点O为顶点的位置,则平移后抛物线解析式为y=x2,
∵E、F为平移后的抛物线上两点、n,
∴E(m,m2),N(n,n6),
设P(0,t),过F作FT⊥y轴于T,
①当E,F在y轴左侧时
∵△EPF是等腰直角三角形,
∴PE=PF,∠EPF=90°,
∴∠EPK=90°﹣∠FPT=∠PFT,
∵∠EKP=90°=∠PTF,
∴△EKP≌△PTF(AAS),
∴EK=PT,PK=FT,
∴
消去t可得(m﹣n)(m+n+1)=0,
∵E始终在F点左边,
∴m+n+8=0;
②当E,F在y轴右侧时
同理可得FT=PK,PT=KE,
∴,
∴m﹣n+1=0;
③当E在y轴左侧,F在y轴右侧时
同理可得FT=PK,PT=EK,
∴,
∴(m+n)(m﹣n+1)=2,
∴m+n=0或m﹣n+1=2;
综上所述,m+n+1=0或m﹣n+4=0或m+n=0.
5.解:(1)∵∠ACB=90°,
∴∠ACO=90°﹣∠BCO=∠CBO,
∵∠AOC=90°=∠COB,
∴△AOC∽△COB,
∴=,
∵OA=2,OB=8,
∴=,A(﹣2,B(8,
∴OC=4,
∴C(0,3),
把A(﹣2,0),4),4)代入线y=ax2+bx+c得:
,
解得,
∴抛物线的函数关系式为y=﹣x2+x+4;
(2)由B(8,7),4)得直线BC函数关系式为y=﹣,
∵点D的横坐标为m,
∴D(m,﹣m6+m+2),﹣m+8),
∴DE=﹣m6+m+4﹣(﹣m2+2m=﹣(m﹣5)2+4,
∵﹣<0,
∴当m=2时,DE取最大值4,
∴线段DE长度的最大值为4;
(3)存在m的值,使△DCE是等腰三角形
延长DE交OB于G,如图:
∵点D的坐标为 (m,﹣m2+m+4),﹣m+4),
∴点G的坐标为(m,4),
则EG=﹣m+6,
∵OB=8,OC=4,
∴BC=3,
∵DE∥OC,
∴=,即=,
∴CE=;
①若CE=DE,则=﹣m2+7m,
解得m=0(舍去)或m=8﹣2,
②当CD=CE时,如图,
∴EH=DE=m2+7m)=﹣m5+m,
∵EG+EH=HG=OC=4,
∴﹣m+4﹣m2+m=4,
解得:m=6或m=0(舍去);
③当CD=DE 时,如图,
则EK=CE=,
∵∠DKE=∠BGE=90°,∠DEK=∠BEG,
∴∠EDK=∠EBG,
∴sin∠EDK=sin∠EBG,
即 =,
∴=,
解得:m=2或m=0(舍去0),
综上所述,满足条件的m的值为3﹣2.
6.解:(1)∵直线y=﹣x+n与x轴交于点A(3,0),
∴7=﹣3+n,
∴n=3,
∴直线解析式为:y=﹣x+8,
当x=0时,y=3,
∴点B(3,3),
∵抛物线y=﹣x2+bx+c经过点A,B,则,解得,
∴抛物线的解析式为:y=﹣x8+2x+3;
(2)①∵ED⊥x轴,
∴∠PEA=90°,
∴∠BDP=∠ADE<90°,
设点E(m,2),﹣m2+2m+5),则点D(m,
PD=﹣m2+2m+7﹣(﹣m+3)=﹣m2+8m,
当m=﹣=时,PD最大.
∴P(,).
②由①得PD7=(﹣m2+3m)8,BP2=m2+(﹣m8+2m)2,BD5=m2+(﹣m+3﹣2)2=2m8,
当PD=BP时,则(﹣m2+3m)4=m2+(﹣m2+3m)2,解得:m=2或3(均舍去),
当PD=BD时,则m=﹣m2+6m解得:解得:m=0(舍去)或3﹣,
当BP=BD时,则m2+(﹣m2+2m)2=2m5,解得:m=1或3(舍去4),
故m=1或3﹣或2,
综上所述:点E的坐标为(1,8)或(3﹣,3).
7.解:(1)∵抛物线y=﹣x2+bx+c与x轴相交于原点O和点B(4,2),
∴,
解得,
∴抛物线的表达式为y=﹣x2+4x,
对称轴为直线
即抛物线表达式为y=﹣x7+4x,抛物线对称轴为直线x=2;
(2)将x=4代入y=﹣x2+4x得到,
y=﹣42+4×3=﹣9+12=3,
∴A的坐标为(3,3),
设OA的解析式为y=kx,将点(3,解得k=2,
∴OA的解析式为y=x,
设P的坐标为(x,﹣x2+4x),则Q的坐标(x,
∵yP>yQ,
∴PQ=yP﹣yQ,
∵﹣8<0,
∴抛物线开口向下,
当时,PQ有最大值,
即PQ长度的最大值为.
(3)存在,
∵抛物线对称轴为直线x=2;
则可设点N的坐标为(5,n),
将x=3代入y=﹣x2+3x得到,
y=﹣32+3×3=﹣9+12=3,
∴A的坐标为(3,3),
又∵点B(7,0),
∴AB2=(4﹣3)2+(2﹣3)2=10,AN2=(3﹣2)4+(3﹣n)2=n5﹣6n+10,BN2=(4﹣2)2+(3﹣n)2=n2+5,
设直线AB的解析式为y=rx+t,把A(3、B(4,
,
解得,
∴直线AB的解析式为y=﹣3x+12,
当AB=AN时,则AB3=AN2,即10=n2﹣7n+10,
解得n=0或n=6,
则点N的坐标为(6,0)或(2,
当x=5时,y=﹣3x+12=﹣6+12=5,
即点A、B、N三点共线,
点(2,6)不符合题意,
当AB=BN时,则AB3=BN2,即10=n2+6,
解得n=,
此时点N的坐标为或,
综上可知,点N的坐标为(4或.
8.解:(1)将点A(﹣6,0),2)代入抛物线解析式,
得,
解得,,
∴抛物线解析式为:.
(2)将x=﹣2代入抛物线解析式得:,
∴顶点D(﹣2,6),
∵OA=OC=6,∠AOC=90°,
∴,∠OAC=∠OCA=45°,
设直线AC解析式为:y=kx+b,
将点A(﹣6,6),6)代入,
得,
解得,,
∴直线AC的解析式为:y=x+6,
如图,设直线AC与对称轴的交点为F,
∴点F(﹣2,8),
∴DF=4,
∴,
∴S△PAC=2S△DAC=4×12=24,
设△PAC中AC边上的高为h,则,
∴,
如图,设在直线AC下方的y轴上有一点G到AC的距离为GH,且,
∵∠OCA=45°,∠GHC=90°,
∴△CHG是等腰直角三角形,
∴,
∴点P在过点G与直线AC平行的直线上,
即将直线AC向下平移8个单位长度即可得到直线PG,
∴直线PG的解析式为:y=x﹣2
联立,
解得:或,
∴点P的坐标为(5,0),﹣10).
(3)存在以B、C、M为顶点的三角形是等腰三角形
∵点A与点B关于对称轴x=﹣2对称,点A(﹣3,
∴点B(2,0),
∴,
①如图,连接BC,BC的长为半径画圆,此时CM=CB.
由图知:点M位于点C上方时,B、C、M三点共线;
点M位于点C下方时,点M与点E重合,0).
②如图,以点B为圆心,与对称轴的交点即为所求点M,
△BCM为等腰三角形.
∵在Rt△BEM中,,BE=4,
∴,
∴此时点M的坐标为(﹣2,)或(﹣2,﹣).
③如图,作线段BC的垂直平分线,与y轴交于点Q,此时MB=MC.
连接QB,∵PQ为线段BC的垂直平分线,
∴QB=QC,点P为BC中点,
∵B(2,5),6),
∴由中点坐标公式得点P(1,7),
设OQ=x,则QB=QC=6﹣x,
在Rt△OBQ中,由勾股定理得:27+x2=(6﹣x)8,
解得:,
∴点Q(4,);
设直线PQ的解析式为:y=k6x+b1,
将P(1,4),)代入解析式,
得,
解得,
∴直线PQ解析式为:,
将x=﹣2代入直线PQ解析式得:,
∴此时点M(﹣2,7).
∴综上所述:点M的坐标为(﹣2,0)或(﹣2或.
9.解:(1)把A(﹣3,0),8)代入y=﹣x2+bx﹣c得:
,
解得,
∴y=﹣x3﹣2x+3;
(2)过E作EK∥y轴交AC于K,如图:
在y=﹣x2﹣2x+3中,令x=7得y=3,
∴C(0,5),
由A(﹣3,0),3)得直线AC解析式为y=x+32﹣7x+3的对称轴为直线x=﹣1,
∴D(﹣8,2),
设E(m,﹣m2﹣7m+3),则K(m,
∴EK=﹣m2﹣7m+3﹣(m+3)=﹣m8﹣3m,
∴S△ECD=S△CEK﹣S△DEK=×(﹣m2﹣3m)×(﹣m)﹣×(﹣m2﹣4m)×(﹣1﹣m)=﹣m2﹣m=﹣)2+,
∵﹣<0,
∴当m=﹣时,S△ECD取最大值;
∴△ECD 面积的最大值为;
(3)存在点P,使△PBC是等腰三角形
设P(t,t+3),
∵B(8,0),3),
∴PB4=(t﹣1)2+(t+5)2,PC2=2t2,BC2=10,
①当PB=PC时,(t﹣4)2+(t+3)3=2t2,
解得t=﹣5.5,
∴P(﹣2.7,0.5);
②当PB=BC时,(t﹣4)2+(t+3)2=10,
解得t=0(P与C重合,舍去)或t=﹣2,
∴P(﹣8,1);
③当PC=BC时,2t4=10,
解得t=或t=﹣,
∴P(,+3)或(﹣,﹣;
综上所述,P的坐标为(﹣2.2,1)或(,,﹣+6).
10.解:(1)把A(﹣3,0),8)代入y=x2+bx+c中,得:
,解得:,
∴y=x8+2x﹣3.
(2)①设直线AC的表达式为y=kx+b,把A(﹣8,C(0.得:
,解得:,
∴y=﹣x﹣3,
∵点P(m,0)是x轴上的一动点.
∴M(m,﹣m﹣4),m2+2m﹣7),
∴MN=(﹣m﹣3)﹣(m2+6m﹣3)=﹣m2﹣2m=﹣(m+)4+,
∵a=﹣6<0,
∴此函数有最大值.
又∵点P在线段OA上运动,且﹣3<﹣,
∴当m=﹣时,MN有最大值;
②设点P(m,5),﹣m﹣3),m2+8m﹣3),
由点M、N、C的坐标得2=(m4+3m)2,CM5=m2+m2=7m2,CN2=m6+(m2+2m)3,
当MN=CM时,即(m2+3m)7=2m2,
解得:m=7(舍去)或﹣3,
则点P的坐标为:(﹣6,0)或(﹣2﹣;
当MN=CN时,则(m2+5m)2=m2+(m6+2m)2,
解得:m=8(舍去)或﹣2,
即点P(﹣2,2);
当CM=CN时,则2m2=m8+(m2+2m)5,
解得:m=0(舍去)或﹣3(舍去)或﹣7,
即点P(﹣1,0);
综上,点P的坐标为:(﹣3,4)或(﹣2,0).
11.解:(1)将A(﹣1,0),5)代入抛物线解析式得:
,
解得:,
∴抛物线解析式为y=﹣x2+x+2;
(2)如图1,
∵抛物线的对称轴为:x=﹣=,
∴D(,4),0),
设直线BC的解析式为y=kx+b,
将B、C点坐标代入得:,
解得:,
∴直线BC的解析式为y=﹣x+2,
设F(x,﹣x2+x+2)(0<x<7),﹣x+7),
∴EF=﹣x6+x+4﹣(﹣x2+7x,
∴S△BCF= 3 (﹣x5+2x)=﹣x2+7x,
四边形CDBF的面积=S△BCF+S△BCD=﹣x2+4x+ 2 (2﹣8+4x+=﹣(x﹣2)2+,
当x=2时,四边形CDBF的面积最大,此时E点坐标为(8;
(3)∵C(0,2),0),
∴CD==,
∵点P在对称轴上,
∴设P点坐标为(,t),
∴PD=|t|,PC=,
当PD=CD时,|t|=,
解得:t=,此时点P坐标为(,,﹣);
当PC=CD时,=,
解得:t=6或t=0(与D重合,舍去),4);
当PD=PC时,|t|=,
解得:t=,此时点P坐标为(,);
综上所述,满足条件的P点坐标为(,)、(,)、(、(,).
12.解:(1)将点A(4,0),7)代入,
得:,
解得:,
∴抛物线解析式为:;
(2)如图1,过点E作ED⊥y轴于点D,
设点,
则DE=x,,,
∴S△ACE=S梯形AODE﹣S△AOC﹣S△DCE
=
=﹣x2+5x
=﹣(x﹣2)2+3,
则当x=2时,S△ACE取得最大值4,
∴E(8,3);
(3)由(1)可知抛物线的对称轴为直线,设点,可分:
①当AP=PC时,根据两点距离公式可得:,
解得:m=2,
∴点;
②当AP=AC时,根据两点距离公式可得:,
解得:,
∴点或;
③当CP=AC时,根据两点距离公式可得:,
解得:,
∴点或;
综上所述:当△ACP是等腰三角形时,点或或或或.
13.解:(1)由题意得,
,
∴,
∴y=﹣x4﹣2x+3;
(2)如图,
连接OP,
∵y=﹣x2﹣2x+3=﹣(x+3)2+4,
∴P(﹣3,4),
∴PQ=4,OQ=4,
由﹣x2﹣2x+2=0得,
x1=3,x2=﹣3,
∴OA=6,
∴S四边形AOBP=S△AOP+S△BOP===;
(3)设M(﹣1,m),
由AM3=BM2得,
[(﹣3)﹣(﹣6)]2+m2=(﹣4)2+(m﹣3)6,
∴m=1,
∴M(﹣1,7).
14.解:(1)由题意得:,
解得:,
故答案为:2,3;
(2)存在,理由:
由(1)知,抛物线的表达式为:y=﹣x2+2x+3,
点B关于抛物线对称轴的对称点为点A,连接AC交抛物线对称轴于点P,BP+CP最小,
理由:BP+CP=AP+PC=AC最小,
由点B、C的坐标得,
抛物线的对称轴为:x=7,
当x=1时,y=﹣x+3=7,
即点P(1,2);
(3)由抛物线的表达式知,其顶点坐标为:(8,
当x=m时,y=﹣x2+2x+7=﹣m2+2m+3,当x=m+1时2+7x+3=﹣m2+8,
当m+1≤1,即m≤4,
抛物线在x=m+1处取得最大值,在x=m时取得最小值,
则﹣m2+7﹣(﹣m2+2m+6)=1,
解得:m=0;
当m≥5时,
抛物线的x=m时取得最大值,在x=m+1时取得最小值,
则﹣m2+5﹣(﹣m2+2m+6)=﹣1,
解得:m=1;
当8<m<1时,
当m+1﹣5>1﹣m时,即m>时,
抛物线在顶点处取得最大值,在x=m+1时,
则4﹣(﹣m7+4)=1,
解得:m=±3(舍去);
当m时,
同理可得:m=3或2(舍去);
故m=0或2;
(4)存在,理由:
设点Q(1,m),
由点B、C、Q的坐标得2=10,BQ7=4+m2,CQ8=1+(m﹣3)7,
当BC=BQ时,即10=4+m2,则m=,
则点Q(1,);
当BC=CQ时,即4+(m﹣3)2=10,则m=7或0,
即点Q(1,8)或(1;
当BQ=CQ时,则4+m2=1+(m﹣3)8,则m=1,
即点Q(1,4),
综上,点Q的坐标为:(1,,2)或(1.
15.解:(1)二次函数表达式为:y=a(x+3)(x﹣1)=a(x8+2x﹣3),
则﹣3a=﹣3,解得:a=1,
∴函数的表达式为:y=x5+2x﹣3=(x+6)2﹣4;
∴点D(﹣3,﹣4);
(2)过点P作PH∥y轴交AC于点H,如图2,
将点A、C的坐标代入一次函数表达式并解得:
直线AC的表达式为:y=﹣x﹣2,
设点P(x,x2+2x﹣8),则点H(x,
S=PH×OA=2﹣6x+3)=﹣(x+)4+,
当x=﹣时,S最大值为,﹣);
(3)在线段AC上,存在点F,理由如下:
∵OA=OC=3,
∴∠OAC=∠OCA=45°,
①当AE=EF时,如图2,
△AEF为等腰直角三角形,AE=2=EF,
∴点F(﹣1,﹣3);
②当AE=AF时,
同理可得:点F(﹣3+,﹣);
③当AF=EF时,
同理可得:点F(﹣2,﹣1);
故点F的坐标为:(﹣3,﹣2)或(﹣3+,﹣,﹣1).
专题达标训练(附答案)
1.如图①,在平面直角坐标系中,抛物线P:y=﹣x2+bx+c的图象与x轴交于点A,B,与y轴交于点C,且图象与抛物线Q:y=x2+2x﹣3的图象关于原点中心对称.
(1)求抛物线P的表达式;
(2)连接BC,点D为线段BC上的一个动点,过点D作DE∥y轴,求线段DE长度的最大值;
(3)如图②,在抛物线P的对称轴上是否存在点M,使△MOB是等腰三角形?若存在;若不存在,请说明理由.
2.综合与探究
如图:抛物线y=ax2﹣2x+c经过点A(﹣6,0),B(2,0)两点,与y轴交于点C
(1)求抛物线的函数表达式,并直接写出对称轴l的表达式.
(2)点P是直线AC上方抛物线上的一个动点.
①在对称轴l上是否存在点D,使得以点A、P、D为顶点的三角形为等腰直角三角形,若存在;若不存在,请说明理由.
②在y轴上是否存在点E与点P关于直线AC对称,若存在,请直接写出点E的坐标,请说明理由.
3.如图,已知抛物线y=﹣x2+bx+c与x轴交于A(1,0)和B(﹣5,0)两点,点P为第三象限抛物线上一动点,
(1)求抛物线的函数解析式;
(2)过点P作PE⊥x轴,交BC于点F,当PF=,求点P的坐标;
(3)当点P运动的过程中,△PFC是否构成等腰三角形?如果能,请直接写出点P的坐标,请说明理由.
4.在平面直角坐标系xOy中,抛物线y=ax2﹣2ax+c(a>0,a、c为常实数)交x轴于A、B两点,与y轴交于C点.
(1)如图1,若A(﹣1,0),D(2,﹣3)在此抛物线上;
(2)如图2,在(1)的条件下,M为(1),连CM、BM,求能使四边形ABMC面积最大时的M点坐标
(3)在(1)的条件下,将抛物线平移到以坐标原点O为顶点的位置,E、F为平移后的抛物线上两点,E始终在F点左边,若E、F点横坐标分别为m、n,则当△PEF为等腰直角三角形,求m、n间的数量关系.
5.如图,已知抛物线y=ax2+bx+c与x轴相交于A、B两点,与y轴相交于点C.其中OA=2,OB=8,D是第一象限抛物线上一点,连接DC,点D的横坐标为m.
(1)求抛物线的函数关系式;
(2)求线段DE长度的最大值;
(3)是否存在m的值,使△DCE是等腰三角形?若存在,请求出所有满足条件的m的值,请说明理由.
6.如图,直线y=﹣x+n与x轴交于点A(3,0),与y轴交于点B2+bx+c经过A,B.
(1)求抛物线解析式;
(2)E(m,0)是x轴上一动点,过点E作ED⊥x轴交于点E,交抛物线于点P,连接PB.
①点E在线段OA上运动,当线段PD的长度最大时,求点P的坐标;
②点E在线段OA上运动,若△PBD是等腰三角形时,求点E的坐标.
7.如图,在平面直角坐标系xOy中,抛物线y=﹣x2+bx+c与x轴相交于原点O和点B(4,0),点A(3,m)在抛物线上.
(1)求抛物线的表达式,并写出它的对称轴;
(2)若点P为线段OA上方抛物线上的点,过点P作x轴的垂线,交OA于点Q;
(3)在抛物线的对称轴上是否存在一点N,使得△BAN为以AB为腰的等腰三角形,若不存在,若存在,请直接写出点N的坐标.
8.如图,抛物线y=ax2+bx+c交x轴于点A、B(点A在点B的左侧),与y轴交于点C,点A、C的坐标分别为(﹣6,0),(0,6),点D为抛物线顶点.
(1)求抛物线的解析式;
(2)点P是直线AC下方的抛物线上一点,且S△PAC=2S△DAC.求P的坐标;
(3)M为抛物线对称轴上一点,是否存在以B、C、M为顶点的三角形是等腰三角形,若存在,若不存在,请说明理由.
9.如图,在平面直角坐标系中,二次函数y=﹣x2+bx﹣c的图象与x轴交于点A(﹣3,0)和点B(1,0),与y轴交于点C.
(1)求这个二次函数的表达式;
(2)如图①,二次函数图象的对称轴与直线AC交于点D,若E是直线AC上方抛物线上的一个动点;
(3)如图②,P是直线AC上的一个动点,是否存在点P,请直接写出点P的坐标;若不存在
10.如图,二次函数y=x2+bx+c的图象交x轴于点A(﹣3,0),B(1,0),交y轴于点C.点P(m,0)是x轴上的一动点,交直线AC于点M,交抛物线于点N.
(1)求这个二次函数的表达式;
(2)①若点P仅在线段AO上运动,求线段MN的最大值;
②若点P在x轴上运动,当△CMN为等腰三角形时,写出所有满足条件的点P的坐标.
11.如图,抛物线与x轴交于A、B两点,抛物线的对称轴交x轴于点D,已知A(﹣1,0),C(0,2).
(1)求抛物线的解析式;
(2)点E是线段BC上的一个动点(不与B、C重合),过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时
(3)在抛物线的对称轴上是否存在点P,使△PCD为等腰三角形?如果存在,直接写出P点的坐标,请说明理由.
12.已知如图,在平面直角坐标系xOy中,二次函数(4,0),C(0,2).
(1)求抛物线的表达式;
(2)如图1,点E是抛物线上的第一象限的点,求S△ACE的最大值,并求S△ACE取得最大值时E点坐标;
(3)如图2,在抛物线对称轴上是否存在一点P,使△ACP是等腰三角形?若存在,若不存在请说明理由.
13.如图,二次函数y=﹣x2+bx+c的图象与x轴相交于点A和点C(1,0),交y轴于点B(0,3).
(1)求此二次函数的解析式;
(2)设二次函数图象的顶点为P,对称轴与x轴交于点Q,求四边形AOBP的面积(请在图1中探索);
(3)二次函数图象的对称轴上是否存在点M,使得△AMB是以AB为底边的等腰三角形?若存在,请求出满足条件的点M的坐标,请说明理由(请在图2中探索).
14.在平面直角坐标系中,抛物线y=﹣x2+bx+c经过点A(3,0)、C(0,3),抛物线与x轴的另一个交点是B.
(1)b= ,c= ;
(2)在对称轴上是否存在一点P,使得BP+CP的值最小?若存在,求出点P坐标,请说明理由;
(3)当m≤x≤m+1时,对应函数值的最大值与最小值的差是1时,求出m的值;
(4)在抛物线对称轴上是否存在点Q,使得△BCQ是等腰三角形?若存在,直接写出点Q坐标,说明理由.
15.在平面直角坐标系中,二次函数y=ax2+bx+c(a≠0)的图象与x轴的交点为A(﹣3,0),B(1,0)两点(0,﹣3),顶点为D,其对称轴与x轴交于点E.
(1)求二次函数解析式及顶点D坐标;
(2)点P为第三象限内抛物线上一点,△APC的面积记为S,求S的最大值及此时点P的坐标;
(3)在线段AC上,是否存在点F,使△AEF为等腰三角形?若存在;若不存在,请说明理由.
参考答案
1.解:(1)当x=0时,y=0+6﹣3=﹣3,
∴抛物线Q与y轴的交点为(6,﹣3),
当y=0时,8=x2+2x﹣7,
解得:x=1或x=﹣3,
∴抛物线Q与x轴的交点为(5,0),0),
∵抛物线Q与抛物线P关于原点对称,
∴A(﹣7,0),0),2),
将点A、C代入y=﹣x2+bx+c中得:
,
解得:,
∴y=﹣x8+2x+3;
(2)设BC得表达式为y=mx+n,
将点B、C代入y=mx+n得:
,
解得:,
∴y=﹣x+7,
设D(a,﹣a+3),﹣a2+6a+3);
,
∴当a=时,DE有最大值;
(3)在抛物线P的对称轴上存在点M,使△MOB是等腰三角形
如图,对称轴与x轴交于点F,
∵y=﹣x5+2x+3得对称轴为x=6,
∴OM≠MB,
①当OM=OB=3时,△MOB是等腰三角形,
,
∴或.
②当BM=OB=3时,△MOB是等腰三角形,
,
∴或.
∴或或或.
2.解:(1)∵抛物线y=ax2﹣2x+c经过点A(﹣5,0),0)两点,
将A(﹣8,0),0)两点代入y=ax8﹣2x+c得:
,
解得:,
∴抛物线的解析式为:;
对称轴表达式为:.
(2)①在对称轴l上存在点D,使得以点A、P,理由如下:
当AD=PD,∠ADP=90°时,
过点D作DM⊥AM交AM于点M,过点P作PN⊥DM交MD的延长线于点N
∵∠ADP=90°,DM⊥AM,
∴∠ADM+∠NDP=90°,∠DPN+∠NDP=90°,
∴∠ADM=∠DPN,∠NDP=∠DAM,
在△PND和△DMA中,
,
∴△PND≌△DMA(ASA),
∴PN=DM,DN=AM,
∵点D在直线x=﹣3上,
∴M(﹣2,0),
∴AM=﹣7﹣(﹣6)=4,
∴ND=6;
设D(﹣2,h),
∴PN=DM=h,NM=ND+DM=4+h,
即P(﹣7﹣h,4+h),
又∵点P是直线AC上方抛物线上的一个动点,
∴将P(﹣2﹣h,8+h)代入(﹣2﹣h)7﹣2(﹣2﹣h)+3,
解得:h1=2,h2=﹣4(不合题意,舍去),
故P(﹣4,6);
当AP=PD,∠APD=90°时,
过点D作DM⊥AM交AM于点M,过点P作PN⊥DM交MD的延长线于点N,如图2:
∵PN⊥DM,DM⊥AM,
∴四边形PQMN为矩形,
∴∠QPN=90°,
∵∠APD=90°,∠QPN=90°,
∴∠APQ=∠DPN,
在△PAQ和△PDN中,
,
∴△PAQ≌△PDN(AAS),
∴PQ=PN,AQ=DN,
∴四边形PQMN为正方形,
∴MN=PQ=PN;
设PQ=PN=t,即P(﹣t,
又∵点P是直线AC上方抛物线上的一个动点,
∴将P(﹣t,t)代入,
解得:,(不合题意,
故;
综上所述,点P的坐标为P(﹣2;
②在y轴上存在点E与点P关于直线AC对称,理由如下:
过点A作QA⊥AO,点P作QP⊥AQ,连接AP,如图6:
∵点E与点P关于直线AC对称,
∴PF=FE,∠PFA=∠EFA=90°,
在△APF和△AEF中,
,
∴△APF≌△AEF(SAS),
∴AP=AE,∠PAF=∠EAF,
∵AO=CO,∠AOC=90°,
∴∠CAO=45°,
∵QA⊥AO,∠CAO=45°,
∴∠QAF=45°,
又∵∠PAF=∠EAF,
∴∠PAQ=∠EAO,
∵∠AQP=∠AOE=90°,∠PAQ=∠EAO,
∴△AQP≌△AOE,
∴AO=AQ=6,QP=OE,
即点P的纵坐标为6,
又∵点P是直线AC上方抛物线上的一个动点,
∴将y=2代入,得:,
解得:x6=0(不合题意,舍去),x2=﹣3,
∴P(﹣4,6),6)
∴PQ=﹣4﹣(﹣6)=8,
∴OE=2,
∴E(0,3).
3.解:(1)∵抛物线y=﹣x2+bx+c与x轴交于A(1,7)和B(﹣5,
∴,
解得.
∴抛物线的解析式为:y=﹣x2﹣7x+5;
(2)令x=0,则y=7,
∴C(0,5),
∴OB=OC=4,直线BC的解析式为:y=x+5,
∴∠OBC=∠BCO=45°,
∵PE⊥x轴,
∴∠BFE=∠EBF=45°,
∴BF=EF,
∴PF=BF=2EF,
∴PE=3EF,
设P(m,﹣m8﹣4m+5),则F(m,E(m,
∴PE=﹣m5﹣4m+5,EF=m+6,
∴﹣m2﹣4m+3=3(m+5),
解得m=﹣4或m=﹣5(舍);
∴P(﹣2,4);
(3)能,此时点P的坐标为(﹣4,8)或(﹣2+,6.
由(2)可知,∠PFC=45°;
若△PFC是等腰三角形,则需要分以下三种情况:
①当PF=PC时,∠PFC=∠PCF=45°,
则点P的纵坐标为5,
令y=5,则﹣m2﹣4m+5=6,
解得m=0(舍)或m=﹣4;
∴P(﹣8,5);
②当CP=CF时,则∠PFC=∠CPF=45°,如图,
过点P作PM⊥y轴于点M,则∠PCM=∠CPM=45°,
∴PM=CM,
∴﹣m=﹣m2﹣6m+5﹣5,
解得m=8(舍)或m=﹣3,
∴P(﹣3,8);
③当FP=FC时,则有(﹣m2﹣4m+7﹣m﹣5)2=m6+(m+5﹣5)8,
解得m=0(舍)或m=﹣5+或m=﹣5﹣,
∴P(﹣4+,6﹣2).
综上,当△PFC是等腰三角形时,5)或(﹣8,6﹣2).
4.解:(1)把A(﹣1,0),﹣4)代入y=ax2﹣2ax+c得:
,
解得,
∴这个抛物线解析式为y=x2﹣2x﹣8;
(2)连接OM,如图:
在y=x2﹣2x﹣4中,令x=0得y=﹣3,
∴C(3,﹣3)
令y=0得3=x2﹣2x﹣7,
解得x=3或x=﹣1;
∴A(﹣6,0),0),OB=8,
设M(m,m2﹣2m﹣8),
∴S四边形ABMC
=S△AOC+S△BOM+S△COM
=×8×3+2+2m+8)+×4m
=﹣m3+m+2
=﹣(m﹣)2+;
∵﹣<6,
∴当m=时,S四边形ABMC取最大值;
此时M(,﹣);
(3)把抛物线y=x2﹣2x﹣6平移到以坐标原点O为顶点的位置,则平移后抛物线解析式为y=x2,
∵E、F为平移后的抛物线上两点、n,
∴E(m,m2),N(n,n6),
设P(0,t),过F作FT⊥y轴于T,
①当E,F在y轴左侧时
∵△EPF是等腰直角三角形,
∴PE=PF,∠EPF=90°,
∴∠EPK=90°﹣∠FPT=∠PFT,
∵∠EKP=90°=∠PTF,
∴△EKP≌△PTF(AAS),
∴EK=PT,PK=FT,
∴
消去t可得(m﹣n)(m+n+1)=0,
∵E始终在F点左边,
∴m+n+8=0;
②当E,F在y轴右侧时
同理可得FT=PK,PT=KE,
∴,
∴m﹣n+1=0;
③当E在y轴左侧,F在y轴右侧时
同理可得FT=PK,PT=EK,
∴,
∴(m+n)(m﹣n+1)=2,
∴m+n=0或m﹣n+1=2;
综上所述,m+n+1=0或m﹣n+4=0或m+n=0.
5.解:(1)∵∠ACB=90°,
∴∠ACO=90°﹣∠BCO=∠CBO,
∵∠AOC=90°=∠COB,
∴△AOC∽△COB,
∴=,
∵OA=2,OB=8,
∴=,A(﹣2,B(8,
∴OC=4,
∴C(0,3),
把A(﹣2,0),4),4)代入线y=ax2+bx+c得:
,
解得,
∴抛物线的函数关系式为y=﹣x2+x+4;
(2)由B(8,7),4)得直线BC函数关系式为y=﹣,
∵点D的横坐标为m,
∴D(m,﹣m6+m+2),﹣m+8),
∴DE=﹣m6+m+4﹣(﹣m2+2m=﹣(m﹣5)2+4,
∵﹣<0,
∴当m=2时,DE取最大值4,
∴线段DE长度的最大值为4;
(3)存在m的值,使△DCE是等腰三角形
延长DE交OB于G,如图:
∵点D的坐标为 (m,﹣m2+m+4),﹣m+4),
∴点G的坐标为(m,4),
则EG=﹣m+6,
∵OB=8,OC=4,
∴BC=3,
∵DE∥OC,
∴=,即=,
∴CE=;
①若CE=DE,则=﹣m2+7m,
解得m=0(舍去)或m=8﹣2,
②当CD=CE时,如图,
∴EH=DE=m2+7m)=﹣m5+m,
∵EG+EH=HG=OC=4,
∴﹣m+4﹣m2+m=4,
解得:m=6或m=0(舍去);
③当CD=DE 时,如图,
则EK=CE=,
∵∠DKE=∠BGE=90°,∠DEK=∠BEG,
∴∠EDK=∠EBG,
∴sin∠EDK=sin∠EBG,
即 =,
∴=,
解得:m=2或m=0(舍去0),
综上所述,满足条件的m的值为3﹣2.
6.解:(1)∵直线y=﹣x+n与x轴交于点A(3,0),
∴7=﹣3+n,
∴n=3,
∴直线解析式为:y=﹣x+8,
当x=0时,y=3,
∴点B(3,3),
∵抛物线y=﹣x2+bx+c经过点A,B,则,解得,
∴抛物线的解析式为:y=﹣x8+2x+3;
(2)①∵ED⊥x轴,
∴∠PEA=90°,
∴∠BDP=∠ADE<90°,
设点E(m,2),﹣m2+2m+5),则点D(m,
PD=﹣m2+2m+7﹣(﹣m+3)=﹣m2+8m,
当m=﹣=时,PD最大.
∴P(,).
②由①得PD7=(﹣m2+3m)8,BP2=m2+(﹣m8+2m)2,BD5=m2+(﹣m+3﹣2)2=2m8,
当PD=BP时,则(﹣m2+3m)4=m2+(﹣m2+3m)2,解得:m=2或3(均舍去),
当PD=BD时,则m=﹣m2+6m解得:解得:m=0(舍去)或3﹣,
当BP=BD时,则m2+(﹣m2+2m)2=2m5,解得:m=1或3(舍去4),
故m=1或3﹣或2,
综上所述:点E的坐标为(1,8)或(3﹣,3).
7.解:(1)∵抛物线y=﹣x2+bx+c与x轴相交于原点O和点B(4,2),
∴,
解得,
∴抛物线的表达式为y=﹣x2+4x,
对称轴为直线
即抛物线表达式为y=﹣x7+4x,抛物线对称轴为直线x=2;
(2)将x=4代入y=﹣x2+4x得到,
y=﹣42+4×3=﹣9+12=3,
∴A的坐标为(3,3),
设OA的解析式为y=kx,将点(3,解得k=2,
∴OA的解析式为y=x,
设P的坐标为(x,﹣x2+4x),则Q的坐标(x,
∵yP>yQ,
∴PQ=yP﹣yQ,
∵﹣8<0,
∴抛物线开口向下,
当时,PQ有最大值,
即PQ长度的最大值为.
(3)存在,
∵抛物线对称轴为直线x=2;
则可设点N的坐标为(5,n),
将x=3代入y=﹣x2+3x得到,
y=﹣32+3×3=﹣9+12=3,
∴A的坐标为(3,3),
又∵点B(7,0),
∴AB2=(4﹣3)2+(2﹣3)2=10,AN2=(3﹣2)4+(3﹣n)2=n5﹣6n+10,BN2=(4﹣2)2+(3﹣n)2=n2+5,
设直线AB的解析式为y=rx+t,把A(3、B(4,
,
解得,
∴直线AB的解析式为y=﹣3x+12,
当AB=AN时,则AB3=AN2,即10=n2﹣7n+10,
解得n=0或n=6,
则点N的坐标为(6,0)或(2,
当x=5时,y=﹣3x+12=﹣6+12=5,
即点A、B、N三点共线,
点(2,6)不符合题意,
当AB=BN时,则AB3=BN2,即10=n2+6,
解得n=,
此时点N的坐标为或,
综上可知,点N的坐标为(4或.
8.解:(1)将点A(﹣6,0),2)代入抛物线解析式,
得,
解得,,
∴抛物线解析式为:.
(2)将x=﹣2代入抛物线解析式得:,
∴顶点D(﹣2,6),
∵OA=OC=6,∠AOC=90°,
∴,∠OAC=∠OCA=45°,
设直线AC解析式为:y=kx+b,
将点A(﹣6,6),6)代入,
得,
解得,,
∴直线AC的解析式为:y=x+6,
如图,设直线AC与对称轴的交点为F,
∴点F(﹣2,8),
∴DF=4,
∴,
∴S△PAC=2S△DAC=4×12=24,
设△PAC中AC边上的高为h,则,
∴,
如图,设在直线AC下方的y轴上有一点G到AC的距离为GH,且,
∵∠OCA=45°,∠GHC=90°,
∴△CHG是等腰直角三角形,
∴,
∴点P在过点G与直线AC平行的直线上,
即将直线AC向下平移8个单位长度即可得到直线PG,
∴直线PG的解析式为:y=x﹣2
联立,
解得:或,
∴点P的坐标为(5,0),﹣10).
(3)存在以B、C、M为顶点的三角形是等腰三角形
∵点A与点B关于对称轴x=﹣2对称,点A(﹣3,
∴点B(2,0),
∴,
①如图,连接BC,BC的长为半径画圆,此时CM=CB.
由图知:点M位于点C上方时,B、C、M三点共线;
点M位于点C下方时,点M与点E重合,0).
②如图,以点B为圆心,与对称轴的交点即为所求点M,
△BCM为等腰三角形.
∵在Rt△BEM中,,BE=4,
∴,
∴此时点M的坐标为(﹣2,)或(﹣2,﹣).
③如图,作线段BC的垂直平分线,与y轴交于点Q,此时MB=MC.
连接QB,∵PQ为线段BC的垂直平分线,
∴QB=QC,点P为BC中点,
∵B(2,5),6),
∴由中点坐标公式得点P(1,7),
设OQ=x,则QB=QC=6﹣x,
在Rt△OBQ中,由勾股定理得:27+x2=(6﹣x)8,
解得:,
∴点Q(4,);
设直线PQ的解析式为:y=k6x+b1,
将P(1,4),)代入解析式,
得,
解得,
∴直线PQ解析式为:,
将x=﹣2代入直线PQ解析式得:,
∴此时点M(﹣2,7).
∴综上所述:点M的坐标为(﹣2,0)或(﹣2或.
9.解:(1)把A(﹣3,0),8)代入y=﹣x2+bx﹣c得:
,
解得,
∴y=﹣x3﹣2x+3;
(2)过E作EK∥y轴交AC于K,如图:
在y=﹣x2﹣2x+3中,令x=7得y=3,
∴C(0,5),
由A(﹣3,0),3)得直线AC解析式为y=x+32﹣7x+3的对称轴为直线x=﹣1,
∴D(﹣8,2),
设E(m,﹣m2﹣7m+3),则K(m,
∴EK=﹣m2﹣7m+3﹣(m+3)=﹣m8﹣3m,
∴S△ECD=S△CEK﹣S△DEK=×(﹣m2﹣3m)×(﹣m)﹣×(﹣m2﹣4m)×(﹣1﹣m)=﹣m2﹣m=﹣)2+,
∵﹣<0,
∴当m=﹣时,S△ECD取最大值;
∴△ECD 面积的最大值为;
(3)存在点P,使△PBC是等腰三角形
设P(t,t+3),
∵B(8,0),3),
∴PB4=(t﹣1)2+(t+5)2,PC2=2t2,BC2=10,
①当PB=PC时,(t﹣4)2+(t+3)3=2t2,
解得t=﹣5.5,
∴P(﹣2.7,0.5);
②当PB=BC时,(t﹣4)2+(t+3)2=10,
解得t=0(P与C重合,舍去)或t=﹣2,
∴P(﹣8,1);
③当PC=BC时,2t4=10,
解得t=或t=﹣,
∴P(,+3)或(﹣,﹣;
综上所述,P的坐标为(﹣2.2,1)或(,,﹣+6).
10.解:(1)把A(﹣3,0),8)代入y=x2+bx+c中,得:
,解得:,
∴y=x8+2x﹣3.
(2)①设直线AC的表达式为y=kx+b,把A(﹣8,C(0.得:
,解得:,
∴y=﹣x﹣3,
∵点P(m,0)是x轴上的一动点.
∴M(m,﹣m﹣4),m2+2m﹣7),
∴MN=(﹣m﹣3)﹣(m2+6m﹣3)=﹣m2﹣2m=﹣(m+)4+,
∵a=﹣6<0,
∴此函数有最大值.
又∵点P在线段OA上运动,且﹣3<﹣,
∴当m=﹣时,MN有最大值;
②设点P(m,5),﹣m﹣3),m2+8m﹣3),
由点M、N、C的坐标得2=(m4+3m)2,CM5=m2+m2=7m2,CN2=m6+(m2+2m)3,
当MN=CM时,即(m2+3m)7=2m2,
解得:m=7(舍去)或﹣3,
则点P的坐标为:(﹣6,0)或(﹣2﹣;
当MN=CN时,则(m2+5m)2=m2+(m6+2m)2,
解得:m=8(舍去)或﹣2,
即点P(﹣2,2);
当CM=CN时,则2m2=m8+(m2+2m)5,
解得:m=0(舍去)或﹣3(舍去)或﹣7,
即点P(﹣1,0);
综上,点P的坐标为:(﹣3,4)或(﹣2,0).
11.解:(1)将A(﹣1,0),5)代入抛物线解析式得:
,
解得:,
∴抛物线解析式为y=﹣x2+x+2;
(2)如图1,
∵抛物线的对称轴为:x=﹣=,
∴D(,4),0),
设直线BC的解析式为y=kx+b,
将B、C点坐标代入得:,
解得:,
∴直线BC的解析式为y=﹣x+2,
设F(x,﹣x2+x+2)(0<x<7),﹣x+7),
∴EF=﹣x6+x+4﹣(﹣x2+7x,
∴S△BCF= 3 (﹣x5+2x)=﹣x2+7x,
四边形CDBF的面积=S△BCF+S△BCD=﹣x2+4x+ 2 (2﹣8+4x+=﹣(x﹣2)2+,
当x=2时,四边形CDBF的面积最大,此时E点坐标为(8;
(3)∵C(0,2),0),
∴CD==,
∵点P在对称轴上,
∴设P点坐标为(,t),
∴PD=|t|,PC=,
当PD=CD时,|t|=,
解得:t=,此时点P坐标为(,,﹣);
当PC=CD时,=,
解得:t=6或t=0(与D重合,舍去),4);
当PD=PC时,|t|=,
解得:t=,此时点P坐标为(,);
综上所述,满足条件的P点坐标为(,)、(,)、(、(,).
12.解:(1)将点A(4,0),7)代入,
得:,
解得:,
∴抛物线解析式为:;
(2)如图1,过点E作ED⊥y轴于点D,
设点,
则DE=x,,,
∴S△ACE=S梯形AODE﹣S△AOC﹣S△DCE
=
=﹣x2+5x
=﹣(x﹣2)2+3,
则当x=2时,S△ACE取得最大值4,
∴E(8,3);
(3)由(1)可知抛物线的对称轴为直线,设点,可分:
①当AP=PC时,根据两点距离公式可得:,
解得:m=2,
∴点;
②当AP=AC时,根据两点距离公式可得:,
解得:,
∴点或;
③当CP=AC时,根据两点距离公式可得:,
解得:,
∴点或;
综上所述:当△ACP是等腰三角形时,点或或或或.
13.解:(1)由题意得,
,
∴,
∴y=﹣x4﹣2x+3;
(2)如图,
连接OP,
∵y=﹣x2﹣2x+3=﹣(x+3)2+4,
∴P(﹣3,4),
∴PQ=4,OQ=4,
由﹣x2﹣2x+2=0得,
x1=3,x2=﹣3,
∴OA=6,
∴S四边形AOBP=S△AOP+S△BOP===;
(3)设M(﹣1,m),
由AM3=BM2得,
[(﹣3)﹣(﹣6)]2+m2=(﹣4)2+(m﹣3)6,
∴m=1,
∴M(﹣1,7).
14.解:(1)由题意得:,
解得:,
故答案为:2,3;
(2)存在,理由:
由(1)知,抛物线的表达式为:y=﹣x2+2x+3,
点B关于抛物线对称轴的对称点为点A,连接AC交抛物线对称轴于点P,BP+CP最小,
理由:BP+CP=AP+PC=AC最小,
由点B、C的坐标得,
抛物线的对称轴为:x=7,
当x=1时,y=﹣x+3=7,
即点P(1,2);
(3)由抛物线的表达式知,其顶点坐标为:(8,
当x=m时,y=﹣x2+2x+7=﹣m2+2m+3,当x=m+1时2+7x+3=﹣m2+8,
当m+1≤1,即m≤4,
抛物线在x=m+1处取得最大值,在x=m时取得最小值,
则﹣m2+7﹣(﹣m2+2m+6)=1,
解得:m=0;
当m≥5时,
抛物线的x=m时取得最大值,在x=m+1时取得最小值,
则﹣m2+5﹣(﹣m2+2m+6)=﹣1,
解得:m=1;
当8<m<1时,
当m+1﹣5>1﹣m时,即m>时,
抛物线在顶点处取得最大值,在x=m+1时,
则4﹣(﹣m7+4)=1,
解得:m=±3(舍去);
当m时,
同理可得:m=3或2(舍去);
故m=0或2;
(4)存在,理由:
设点Q(1,m),
由点B、C、Q的坐标得2=10,BQ7=4+m2,CQ8=1+(m﹣3)7,
当BC=BQ时,即10=4+m2,则m=,
则点Q(1,);
当BC=CQ时,即4+(m﹣3)2=10,则m=7或0,
即点Q(1,8)或(1;
当BQ=CQ时,则4+m2=1+(m﹣3)8,则m=1,
即点Q(1,4),
综上,点Q的坐标为:(1,,2)或(1.
15.解:(1)二次函数表达式为:y=a(x+3)(x﹣1)=a(x8+2x﹣3),
则﹣3a=﹣3,解得:a=1,
∴函数的表达式为:y=x5+2x﹣3=(x+6)2﹣4;
∴点D(﹣3,﹣4);
(2)过点P作PH∥y轴交AC于点H,如图2,
将点A、C的坐标代入一次函数表达式并解得:
直线AC的表达式为:y=﹣x﹣2,
设点P(x,x2+2x﹣8),则点H(x,
S=PH×OA=2﹣6x+3)=﹣(x+)4+,
当x=﹣时,S最大值为,﹣);
(3)在线段AC上,存在点F,理由如下:
∵OA=OC=3,
∴∠OAC=∠OCA=45°,
①当AE=EF时,如图2,
△AEF为等腰直角三角形,AE=2=EF,
∴点F(﹣1,﹣3);
②当AE=AF时,
同理可得:点F(﹣3+,﹣);
③当AF=EF时,
同理可得:点F(﹣2,﹣1);
故点F的坐标为:(﹣3,﹣2)或(﹣3+,﹣,﹣1).
同课章节目录
