冀教版数学八年级下册19.2 平面直角坐标系 第2课时课件(共15张PPT)
文档属性
| 名称 | 冀教版数学八年级下册19.2 平面直角坐标系 第2课时课件(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 201.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-18 20:42:11 | ||
图片预览




文档简介
(共15张PPT)
第2课时
第十九章 平面直角坐标系
19.2 平面直角坐标系
1.掌握平面直角坐标系各象限、坐标轴上点的坐标特征;
2.掌握点关于坐标轴及原点的对称点的坐标特征.
合作探究
当堂检测
学习目标
课堂总结
自主学习
合作探究
当堂检测
学习目标
课堂总结
自主学习
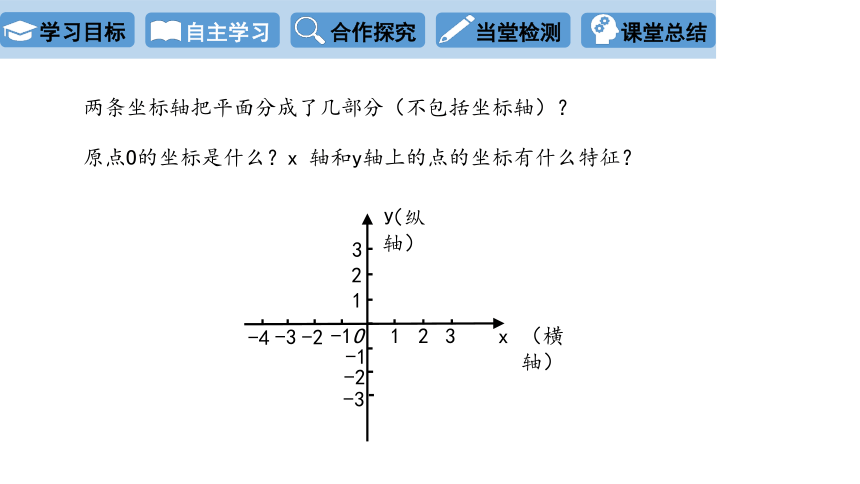
两条坐标轴把平面分成了几部分(不包括坐标轴)?
原点O的坐标是什么?x 轴和y轴上的点的坐标有什么特征?
y
O
x
1
2
3
1
2
3
-1
-2
-3
-4
-1
-2
-3
(纵轴)
(横轴)
合作探究
当堂检测
学习目标
课堂总结
自主学习
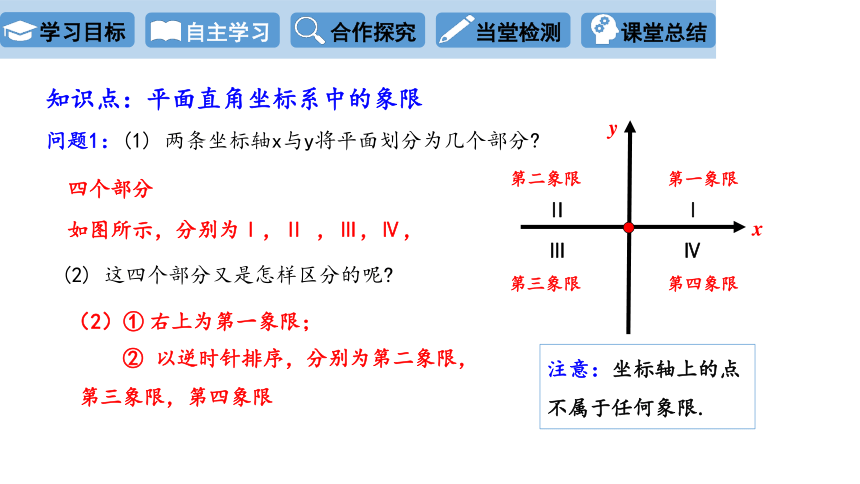
知识点:平面直角坐标系中的象限
问题1:(1) 两条坐标轴x与y将平面划分为几个部分
y
四个部分
第一象限
第二象限
第三象限
第四象限
x
如图所示,分别为Ⅰ,Ⅱ ,Ⅲ,Ⅳ,
Ⅰ
Ⅱ
Ⅲ
Ⅳ
(2) 这四个部分又是怎样区分的呢
(2)① 右上为第一象限;
注意:坐标轴上的点不属于任何象限.
② 以逆时针排序,分别为第二象限,第三象限,第四象限
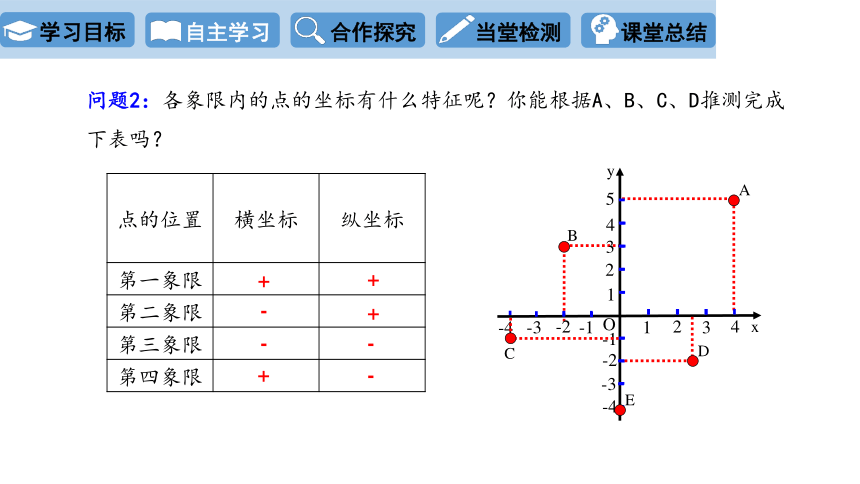
问题2:各象限内的点的坐标有什么特征呢?你能根据A、B、C、D推测完成下表吗?
点的位置 横坐标 纵坐标
第一象限
第二象限
第三象限
第四象限
+
+
+
-
-
-
+
-
A
y
O
x
-1
-2
-3
-1
-2
-3
-4
1
2
3
4
1
2
3
4
5
-4
B
C
D
E
合作探究
当堂检测
学习目标
课堂总结
自主学习
探究:直角坐标系中对称点的坐标的特征
合作探究
当堂检测
学习目标
课堂总结
自主学习
如图,分别写出点A(1,3)关于x轴的对称点坐标,关于y轴的对称点坐标,关于原点的对称点坐标.
-4 -3 -2 -1O 1 2 3 4 x
y
4321
-1
-2
-3
-4
问题1:这些对称点的坐标特征分别是什么?
A(1,3)
A'(1,-3)
A''(-1,3)
A'''
(-1,-3)
关于y轴对称的两点,横坐标互为相反数,纵坐标相等;
关于x轴对称的两点,横坐标相等,纵坐标互为相反数;
关于原点对称的两点,横坐标和纵坐标都互为相反数.
练一练:
1. 点(4,3)与点(4,-3)的关系是( )
A.关于原点对称
B.关于x轴对称
C.关于y轴对称
D.不能构成对称关系
分析:两个点横坐标相等,纵坐标互为相反数,故关于x轴对称.
B
合作探究
当堂检测
学习目标
课堂总结
自主学习
问题2:如图,直线l∥x轴,m∥y轴,观察l,m上点的坐标有怎样的特征?
合作探究
当堂检测
学习目标
课堂总结
自主学习
O
1
-1
1
-1
x
y
l
m
平行于y轴的直线上的各点的横坐标相同,纵坐标不同.
平行于x轴的直线上的各点的纵坐标相同,
横坐标不同.
合作探究
当堂检测
学习目标
课堂总结
自主学习
O
1
2
3
4
-3
-2
-1
3
1
4
2
-2
-4
-1
-3
y
A
B
C
D
问题3:两坐标轴夹角的平分线上的点的坐标有何特点?
x
一、三象限的角平分线上的点的横纵坐标相等, 二、四象限的角平分线上的点的横纵坐标互为相反数.
1.在平面直角坐标系中,若点A(a,-b)在第一象限内,则点B(a,b)所在的象限是( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
合作探究
当堂检测
学习目标
课堂总结
自主学习
D
解析:∵点A再第一象限,
∴a>0,b<0,
∴点B在第四象限
2.点(m,-1)和点(2,n)关于x轴对称,则mn等于( )
A.- 2 B.2
C.1 D.- 1
合作探究
当堂检测
学习目标
课堂总结
自主学习
解析:两点关于x轴对称,
∴mn=2
∴ m = 2, n = 1 ,
∴两点横坐标相等,纵坐标相反,
B
3.已知点P(a-2,2a+8),分别根据下列条件求出点P的坐标.
(1)点P在x轴上;
(2)点P在y轴上;
解:(1)∵点P(a-2,2a+8)在x轴上,
合作探究
当堂检测
学习目标
课堂总结
自主学习
∴2a+8=0,解得a=-4,
故a-2=-4-2=-6,则P(-6,0);
(2)∵点P(a-2,2a+8)在y轴上,
∴a-2=0,解得a=2,
故2a+8=2×2+8=12,则P(0,12);
3.已知点P(a-2,2a+8),分别根据下列条件求出点P的坐标.
(3)点Q的坐标为(1,5),直线PQ∥y轴;
合作探究
当堂检测
学习目标
课堂总结
自主学习
(3)∵点Q的坐标为(1,5),直线PQ∥y轴,
∴a-2=1,解得a=3,
故2a+8=14,则P(1,14);
3.已知点P(a-2,2a+8),分别根据下列条件求出点P的坐标.
(4)点P到x轴、y轴的距离相等.
合作探究
当堂检测
学习目标
课堂总结
自主学习
(4)∵点P到x轴、y轴的距离相等,
∴a-2=2a+8或a-2+2a+8=0,
解得a=-10或a=-2,
故当a=-10时,则a-2=-12,2a+8=-12
则P(-12,-12);
故当a=-2时,则a-2=-4,2a+8=4,
则P(-4,4).
综上所述,P(-12,-12)或(-4,4).
合作探究
当堂检测
学习目标
课堂总结
自主学习
点的位置与点的坐标的关系
象限的概念
关于x轴、y轴、原点对称点的坐标的特点
点的位置与坐标的关系
第2课时
第十九章 平面直角坐标系
19.2 平面直角坐标系
1.掌握平面直角坐标系各象限、坐标轴上点的坐标特征;
2.掌握点关于坐标轴及原点的对称点的坐标特征.
合作探究
当堂检测
学习目标
课堂总结
自主学习
合作探究
当堂检测
学习目标
课堂总结
自主学习
两条坐标轴把平面分成了几部分(不包括坐标轴)?
原点O的坐标是什么?x 轴和y轴上的点的坐标有什么特征?
y
O
x
1
2
3
1
2
3
-1
-2
-3
-4
-1
-2
-3
(纵轴)
(横轴)
合作探究
当堂检测
学习目标
课堂总结
自主学习
知识点:平面直角坐标系中的象限
问题1:(1) 两条坐标轴x与y将平面划分为几个部分
y
四个部分
第一象限
第二象限
第三象限
第四象限
x
如图所示,分别为Ⅰ,Ⅱ ,Ⅲ,Ⅳ,
Ⅰ
Ⅱ
Ⅲ
Ⅳ
(2) 这四个部分又是怎样区分的呢
(2)① 右上为第一象限;
注意:坐标轴上的点不属于任何象限.
② 以逆时针排序,分别为第二象限,第三象限,第四象限
问题2:各象限内的点的坐标有什么特征呢?你能根据A、B、C、D推测完成下表吗?
点的位置 横坐标 纵坐标
第一象限
第二象限
第三象限
第四象限
+
+
+
-
-
-
+
-
A
y
O
x
-1
-2
-3
-1
-2
-3
-4
1
2
3
4
1
2
3
4
5
-4
B
C
D
E
合作探究
当堂检测
学习目标
课堂总结
自主学习
探究:直角坐标系中对称点的坐标的特征
合作探究
当堂检测
学习目标
课堂总结
自主学习
如图,分别写出点A(1,3)关于x轴的对称点坐标,关于y轴的对称点坐标,关于原点的对称点坐标.
-4 -3 -2 -1O 1 2 3 4 x
y
4321
-1
-2
-3
-4
问题1:这些对称点的坐标特征分别是什么?
A(1,3)
A'(1,-3)
A''(-1,3)
A'''
(-1,-3)
关于y轴对称的两点,横坐标互为相反数,纵坐标相等;
关于x轴对称的两点,横坐标相等,纵坐标互为相反数;
关于原点对称的两点,横坐标和纵坐标都互为相反数.
练一练:
1. 点(4,3)与点(4,-3)的关系是( )
A.关于原点对称
B.关于x轴对称
C.关于y轴对称
D.不能构成对称关系
分析:两个点横坐标相等,纵坐标互为相反数,故关于x轴对称.
B
合作探究
当堂检测
学习目标
课堂总结
自主学习
问题2:如图,直线l∥x轴,m∥y轴,观察l,m上点的坐标有怎样的特征?
合作探究
当堂检测
学习目标
课堂总结
自主学习
O
1
-1
1
-1
x
y
l
m
平行于y轴的直线上的各点的横坐标相同,纵坐标不同.
平行于x轴的直线上的各点的纵坐标相同,
横坐标不同.
合作探究
当堂检测
学习目标
课堂总结
自主学习
O
1
2
3
4
-3
-2
-1
3
1
4
2
-2
-4
-1
-3
y
A
B
C
D
问题3:两坐标轴夹角的平分线上的点的坐标有何特点?
x
一、三象限的角平分线上的点的横纵坐标相等, 二、四象限的角平分线上的点的横纵坐标互为相反数.
1.在平面直角坐标系中,若点A(a,-b)在第一象限内,则点B(a,b)所在的象限是( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
合作探究
当堂检测
学习目标
课堂总结
自主学习
D
解析:∵点A再第一象限,
∴a>0,b<0,
∴点B在第四象限
2.点(m,-1)和点(2,n)关于x轴对称,则mn等于( )
A.- 2 B.2
C.1 D.- 1
合作探究
当堂检测
学习目标
课堂总结
自主学习
解析:两点关于x轴对称,
∴mn=2
∴ m = 2, n = 1 ,
∴两点横坐标相等,纵坐标相反,
B
3.已知点P(a-2,2a+8),分别根据下列条件求出点P的坐标.
(1)点P在x轴上;
(2)点P在y轴上;
解:(1)∵点P(a-2,2a+8)在x轴上,
合作探究
当堂检测
学习目标
课堂总结
自主学习
∴2a+8=0,解得a=-4,
故a-2=-4-2=-6,则P(-6,0);
(2)∵点P(a-2,2a+8)在y轴上,
∴a-2=0,解得a=2,
故2a+8=2×2+8=12,则P(0,12);
3.已知点P(a-2,2a+8),分别根据下列条件求出点P的坐标.
(3)点Q的坐标为(1,5),直线PQ∥y轴;
合作探究
当堂检测
学习目标
课堂总结
自主学习
(3)∵点Q的坐标为(1,5),直线PQ∥y轴,
∴a-2=1,解得a=3,
故2a+8=14,则P(1,14);
3.已知点P(a-2,2a+8),分别根据下列条件求出点P的坐标.
(4)点P到x轴、y轴的距离相等.
合作探究
当堂检测
学习目标
课堂总结
自主学习
(4)∵点P到x轴、y轴的距离相等,
∴a-2=2a+8或a-2+2a+8=0,
解得a=-10或a=-2,
故当a=-10时,则a-2=-12,2a+8=-12
则P(-12,-12);
故当a=-2时,则a-2=-4,2a+8=4,
则P(-4,4).
综上所述,P(-12,-12)或(-4,4).
合作探究
当堂检测
学习目标
课堂总结
自主学习
点的位置与点的坐标的关系
象限的概念
关于x轴、y轴、原点对称点的坐标的特点
点的位置与坐标的关系
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
