冀教版数学七年级下册10.4 一元一次不等式的应用 课件(共18张PPT)
文档属性
| 名称 | 冀教版数学七年级下册10.4 一元一次不等式的应用 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 158.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-18 20:56:41 | ||
图片预览






文档简介
(共18张PPT)
第十章 一元一次不等式和一元一次不等式组
10.4 一元一次不等式的应用
学习导航
学习目标
新课导入
合作探究
当堂检测
课堂总结
一、学习目标
1.会从实际问题中抽象出数学模型;
2.会列一元一次不等式,解决相关数学问题和实际问题.
二、新课导入
回顾与思考
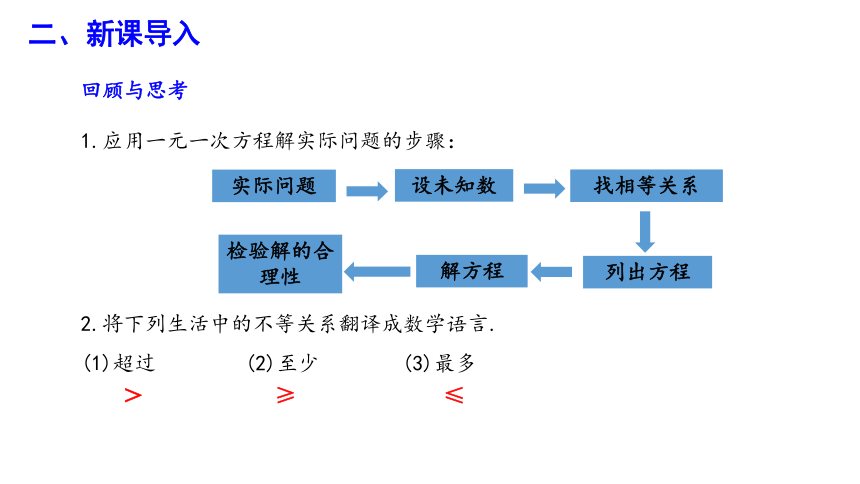
1.应用一元一次方程解实际问题的步骤:
实际问题
找相等关系
设未知数
列出方程
检验解的合理性
解方程
2.将下列生活中的不等关系翻译成数学语言.
(1)超过
(2)至少
(3)最多
≥
≤
>
三、合作探究
探究一 利用一元一次不等式解决简单的实际问题
去年某市空气质量良好(二级以上)的天数与全年天数(365)之比
达到60%,如果明年(365天)这样的比值要超过70%,那么明年空气质量良
好的天数要比去年至少增加多少?
问题1 此实际问题中的不等关系是什么?
明年空气质量良好的天数÷明年天数>70%.
三、合作探究
问题2 设x表示明年增加的空气质量良好的天数,则明年空气质量是良好的
天数是多少?
x+365×60%.
问题3 你能列出不等式并解出来吗?
(x+365×60%)÷365>70%,
x>36.5.
x+219>255.5,
问题4 你能给出一个合理化的答案吗?
明年要比去年空气质量良好的天数至少增加37,才能使这一年空气质量良好
的天数超过全年天数的70%.
练一练
三、合作探究
1.某童装店按每套90元的价格购进40套童装,应缴纳的税费为销售额的10%. 如果要获得不低于900元的纯利润,每套童装的售价至少是多少元?
解:
则 40x-90×40-40x·10%≥900.
解得 x ≥ 125.
答:每套童装的售价至少是125元.
分析:本题数量关系:销售额-成本-税费≥纯利润(900元).
设每套童装的售价是 x 元.
三、合作探究
探究二 利用一元一次不等式解决方案选择问题
甲、乙两商场以同样的价格出售同样的商品,并且又各自推出不同的优惠
方案:在甲商场累计购买100元后,超出100元的部分按90%收费;在乙商场
累计购买超过50元后,超过50元的部分按95%收费.顾客到哪家商场购物花
费少
问题1 你是如何理解题意的呢?
三、合作探究
问题2 如果购物款为x元,你能分别表示出在两家商场花费的钱数吗
购物款 甲商场 乙商场
0<x≤50
50<x≤100
x>100
50+0.95(x-50)
100+0.9(x-100)
x
x
x
50+0.95(x-50)
方案:在甲商场累计购买100元后,超出100元的部分按90%收费;在乙商场
累计购买超过50元后,超过50元的部分按95%收费.
三、合作探究
问题3 你能看出在哪个商场花费少吗?
购物款 甲商场 乙商场 比较
0<x≤50 x x
50<x≤100 x 50+0.95(x-50)
x>100 100+0.9(x-100) 50+0.95(x-50)
一样
乙少
不确定
x-[50+0.95(x-50)]=0.5x-5
因为50<x≤100,所以0.5x-5>0,即甲花费多
三、合作探究
问题4 如果累计购物超过100元,在哪家商场花费少呢?
提示:什么情况下,到甲商场购物花费少?什么情况下,到乙商场购物花费少?
什么情况下,两商场花费一样?
若在甲商场花费少,则
100+0.9(x-100)<50+0.95(x-50);
解得x>150;
若在乙商场花费少,则
100+0.9(x-100)>50+0.95(x-50);
解得x<150;
两商场花费一样
100+0.9(x-100)=50+0.95(x-50);
解得x=150.
三、合作探究
问题5 你能综合上面分析给出一个合理化的消费方案吗?
购物不超过50元和刚好是150元时, 在两家商场购物没有区别;
超过50元而不到150元时在乙商场购物花费少;超过150元后,
在甲商场购物花费少.
归纳总结:最优方案的选择,主要是通过比较两种方案间的大小关系,
从而确定出最优方案的范围或条件.
练一练
三、合作探究
3.某校组织七年级师生共480人春游,现有25座和45座(均含司机座位)两种汽车可供租用.已知25座客车的租金为205元/辆,45座客车的租金为370元/辆.
(1)若单独租用一种客车,请你通过计算说明租用哪种汽车更划算?
解:单独租用25座客车:
480÷(25-1)=20
20×205=4100(元)
单独租用45座客车:
480÷(45-1)≈10.9 取11
11×370=4070(元)
答:单独租用45座客车更划算.
三、合作探究
3.某校组织七年级师生共480人春游,现有25座和45座(均含司机座位)两种汽车可供租用.已知25座客车的租金为205元/辆,45座客车的租金为370元/辆.
(2)该校决定这次春游同时租用这两种车辆.若45座客车比25座客车少租3辆,则45座客车最少需租用多少辆?这样的租车方式比单独租用一种车辆合算吗?说明你的理由.
解:租用45座客车x辆:
(45-1)x+(25-1)(x+3)≥480
44x+24x+72≥480
x≥6 则租用45座客车6辆,25座车租用9辆
6×370+9×205=4065(元)
答:这种租车方式比单独租一种客车更划算.
<4070(元)
四、当堂检测
1.小明家的客厅长5 m,宽4 m.现在想购买边长为60cm的正方形地砖把地
面铺满,至少需要购买多少块这样的地板砖?
解:设需要购买x块地板砖,则有
答:小明家至少要购买56块这样的地板砖.
由于地板砖的数目必须是整数,所以x的最小值为56.
解得x ≥ 55.6.
5×4≤0.6×0.6x.
四、当堂检测
2.一次环保知识竞赛共有25道题,规定答对一道题得4分,答错或不答一道
题扣1分.在这次竞赛中,小明被评为优秀(85分或85分以上),小明至少答
对了几道题?
分析: 本题涉及的数量关系是:总得分≥85.
解:设小明答对了 x 道题,则他答错和不答的共有 (25-x)道题.
根据题意,得 4x-1×(25-x)≥85.
解这个不等式,得 x ≥ 22.
所以,小明至少答对了22道题.
四、当堂检测
3.某市打市内电话的收费标准是:每次3 min以内(含3 min)0.22元,以后
每分钟0.11元(不足1 min部分按1 min计).小琴一天在家里给同学打了一
次市内电话,所用电话费低于0.55元.她最多打了几分钟的电话?
解:设小琴最多打了x分钟的电话,则有
答:小琴最多打了5min的电话.
由于电话计时按照分钟计时,x应是整数,所以x的最大值为5.
解得 x <6
0.22+ (x-3) ×0.11<0.55
五、课堂总结
一元一次不等式的应用
实际问题
根据题意列不等式
解一元一次不等式
根据实际问题找出符合条件的解集或整数解
得出解决问题的答案
第十章 一元一次不等式和一元一次不等式组
10.4 一元一次不等式的应用
学习导航
学习目标
新课导入
合作探究
当堂检测
课堂总结
一、学习目标
1.会从实际问题中抽象出数学模型;
2.会列一元一次不等式,解决相关数学问题和实际问题.
二、新课导入
回顾与思考
1.应用一元一次方程解实际问题的步骤:
实际问题
找相等关系
设未知数
列出方程
检验解的合理性
解方程
2.将下列生活中的不等关系翻译成数学语言.
(1)超过
(2)至少
(3)最多
≥
≤
>
三、合作探究
探究一 利用一元一次不等式解决简单的实际问题
去年某市空气质量良好(二级以上)的天数与全年天数(365)之比
达到60%,如果明年(365天)这样的比值要超过70%,那么明年空气质量良
好的天数要比去年至少增加多少?
问题1 此实际问题中的不等关系是什么?
明年空气质量良好的天数÷明年天数>70%.
三、合作探究
问题2 设x表示明年增加的空气质量良好的天数,则明年空气质量是良好的
天数是多少?
x+365×60%.
问题3 你能列出不等式并解出来吗?
(x+365×60%)÷365>70%,
x>36.5.
x+219>255.5,
问题4 你能给出一个合理化的答案吗?
明年要比去年空气质量良好的天数至少增加37,才能使这一年空气质量良好
的天数超过全年天数的70%.
练一练
三、合作探究
1.某童装店按每套90元的价格购进40套童装,应缴纳的税费为销售额的10%. 如果要获得不低于900元的纯利润,每套童装的售价至少是多少元?
解:
则 40x-90×40-40x·10%≥900.
解得 x ≥ 125.
答:每套童装的售价至少是125元.
分析:本题数量关系:销售额-成本-税费≥纯利润(900元).
设每套童装的售价是 x 元.
三、合作探究
探究二 利用一元一次不等式解决方案选择问题
甲、乙两商场以同样的价格出售同样的商品,并且又各自推出不同的优惠
方案:在甲商场累计购买100元后,超出100元的部分按90%收费;在乙商场
累计购买超过50元后,超过50元的部分按95%收费.顾客到哪家商场购物花
费少
问题1 你是如何理解题意的呢?
三、合作探究
问题2 如果购物款为x元,你能分别表示出在两家商场花费的钱数吗
购物款 甲商场 乙商场
0<x≤50
50<x≤100
x>100
50+0.95(x-50)
100+0.9(x-100)
x
x
x
50+0.95(x-50)
方案:在甲商场累计购买100元后,超出100元的部分按90%收费;在乙商场
累计购买超过50元后,超过50元的部分按95%收费.
三、合作探究
问题3 你能看出在哪个商场花费少吗?
购物款 甲商场 乙商场 比较
0<x≤50 x x
50<x≤100 x 50+0.95(x-50)
x>100 100+0.9(x-100) 50+0.95(x-50)
一样
乙少
不确定
x-[50+0.95(x-50)]=0.5x-5
因为50<x≤100,所以0.5x-5>0,即甲花费多
三、合作探究
问题4 如果累计购物超过100元,在哪家商场花费少呢?
提示:什么情况下,到甲商场购物花费少?什么情况下,到乙商场购物花费少?
什么情况下,两商场花费一样?
若在甲商场花费少,则
100+0.9(x-100)<50+0.95(x-50);
解得x>150;
若在乙商场花费少,则
100+0.9(x-100)>50+0.95(x-50);
解得x<150;
两商场花费一样
100+0.9(x-100)=50+0.95(x-50);
解得x=150.
三、合作探究
问题5 你能综合上面分析给出一个合理化的消费方案吗?
购物不超过50元和刚好是150元时, 在两家商场购物没有区别;
超过50元而不到150元时在乙商场购物花费少;超过150元后,
在甲商场购物花费少.
归纳总结:最优方案的选择,主要是通过比较两种方案间的大小关系,
从而确定出最优方案的范围或条件.
练一练
三、合作探究
3.某校组织七年级师生共480人春游,现有25座和45座(均含司机座位)两种汽车可供租用.已知25座客车的租金为205元/辆,45座客车的租金为370元/辆.
(1)若单独租用一种客车,请你通过计算说明租用哪种汽车更划算?
解:单独租用25座客车:
480÷(25-1)=20
20×205=4100(元)
单独租用45座客车:
480÷(45-1)≈10.9 取11
11×370=4070(元)
答:单独租用45座客车更划算.
三、合作探究
3.某校组织七年级师生共480人春游,现有25座和45座(均含司机座位)两种汽车可供租用.已知25座客车的租金为205元/辆,45座客车的租金为370元/辆.
(2)该校决定这次春游同时租用这两种车辆.若45座客车比25座客车少租3辆,则45座客车最少需租用多少辆?这样的租车方式比单独租用一种车辆合算吗?说明你的理由.
解:租用45座客车x辆:
(45-1)x+(25-1)(x+3)≥480
44x+24x+72≥480
x≥6 则租用45座客车6辆,25座车租用9辆
6×370+9×205=4065(元)
答:这种租车方式比单独租一种客车更划算.
<4070(元)
四、当堂检测
1.小明家的客厅长5 m,宽4 m.现在想购买边长为60cm的正方形地砖把地
面铺满,至少需要购买多少块这样的地板砖?
解:设需要购买x块地板砖,则有
答:小明家至少要购买56块这样的地板砖.
由于地板砖的数目必须是整数,所以x的最小值为56.
解得x ≥ 55.6.
5×4≤0.6×0.6x.
四、当堂检测
2.一次环保知识竞赛共有25道题,规定答对一道题得4分,答错或不答一道
题扣1分.在这次竞赛中,小明被评为优秀(85分或85分以上),小明至少答
对了几道题?
分析: 本题涉及的数量关系是:总得分≥85.
解:设小明答对了 x 道题,则他答错和不答的共有 (25-x)道题.
根据题意,得 4x-1×(25-x)≥85.
解这个不等式,得 x ≥ 22.
所以,小明至少答对了22道题.
四、当堂检测
3.某市打市内电话的收费标准是:每次3 min以内(含3 min)0.22元,以后
每分钟0.11元(不足1 min部分按1 min计).小琴一天在家里给同学打了一
次市内电话,所用电话费低于0.55元.她最多打了几分钟的电话?
解:设小琴最多打了x分钟的电话,则有
答:小琴最多打了5min的电话.
由于电话计时按照分钟计时,x应是整数,所以x的最大值为5.
解得 x <6
0.22+ (x-3) ×0.11<0.55
五、课堂总结
一元一次不等式的应用
实际问题
根据题意列不等式
解一元一次不等式
根据实际问题找出符合条件的解集或整数解
得出解决问题的答案
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
