10.3 解一元一次不等式 (第1课时) 课件 22张PPT 冀教版数学七年级下册
文档属性
| 名称 | 10.3 解一元一次不等式 (第1课时) 课件 22张PPT 冀教版数学七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 622.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-18 00:00:00 | ||
图片预览







文档简介
(共22张PPT)
10.3 解一元一次不等式
第1课时
第十章 一元一次不等式和一元一次不等式组
学习导航
学习目标
新课导入
自主学习
合作探究
当堂检测
课堂总结
一、学习目标
1.知道不等式的解、不等式的解集、解不等式等、一元一次不等式概念;
2.会解简单的不等式,并能用数轴正确表示不等式的解集.
二、新课导入
上节课学习的不等式的基本性质有哪些?
根据不等式的基本性质,怎么解一元一次不等式呢?
不等式的性质1:如果 a > b,那么 a ± c > b ± c,
不等式的性质2:如果a>b,c>0,那么 ac>bc,
不等式的性质3:如果a > b,c < 0,那么 ac < bc.
问题1:下面给出的数中,能使不等式x>50成立吗?
知识点一: 不等式的解与解集
20, 40, 50, 100.
解:当x=20,20<50,不成立;
当x=100,100>50,成立.
当x=50,50=50,不成立;
当x=40,40<50,不成立;
归纳总结:
对于含有未知数的不等式,能使不等式成立的未知数的值,叫做不等式的解.
三、自主学习
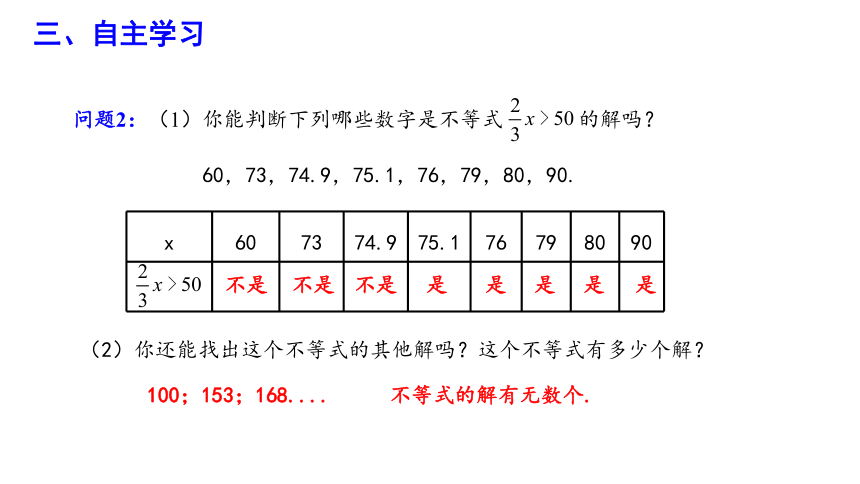
问题2:(1)你能判断下列哪些数字是不等式 的解吗?
三、自主学习
60,73,74.9,75.1,76,79,80,90.
x 60 73 74.9 75.1 76 79 80 90
不是
是
是
不是
不是
是
是
是
100;153;168....
(2)你还能找出这个不等式的其他解吗?这个不等式有多少个解?
不等式的解有无数个.
问题2:(3)你发现了哪些数是这个不等式的解?你从表格中发现了什么规律?
一般的,一个含有未知数的不等式的所有的解组成这个不等式的解集.
三、自主学习
只要x的值大于75就是这个不等式的解.
求不等式的解集的过程叫做解不等式.
x 60 73 74.9 75.1 76 79 80 90
不是
是
是
不是
不是
是
是
是
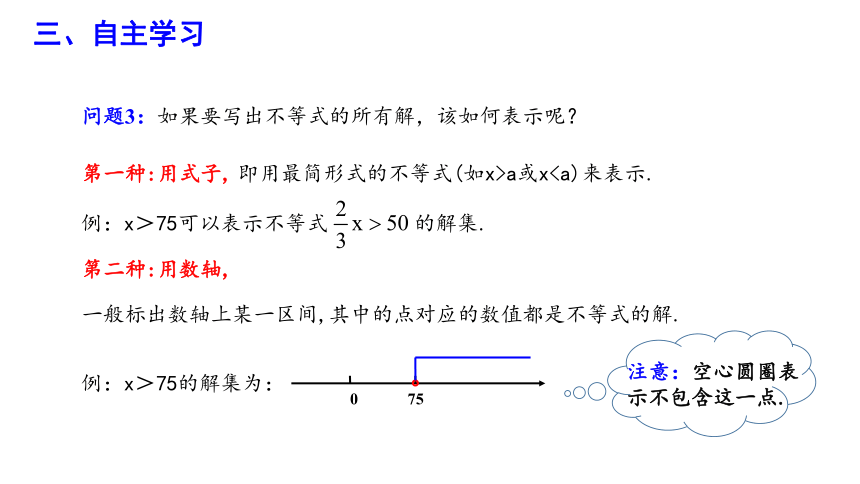
问题3:如果要写出不等式的所有解,该如何表示呢?
0
75
例:x>75的解集为:
三、自主学习
第一种:用式子,
即用最简形式的不等式(如x>a或x例:x>75可以表示不等式 的解集.
第二种:用数轴,
一般标出数轴上某一区间,其中的点对应的数值都是不等式的解.
注意:空心圆圈表示不包含这一点.
不等式的解 不等式的解集
区别 定义
特点
形式
联系
满足一个不等式的未知数
的某个值
满足一个不等式的未知数的所有值
个体
全体
x = 0.9 是 7 + 5x< 12的一个解
x < 1 是 7 + 5x < 12 的 解集
某个解一定是解集中的一员
解集一定包括了某个解
问题4:不等式的解和解集有什么区别与联系呢?
三、自主学习
问题:什么是一元一次方程?
三、自主学习
只含一个未知数、未知数的次数都是1且两边都是整式的等式.
思考:根据一元一次方程的定义,你能猜出一元一次不等式的定义吗?
含有 ,并且 的不等式叫做一元一次不等式.
一个未知数
未知数的次数都是1
知识点二: 一元一次不等式
三、自主学习
像x>3,y≤0,7 + 5x ≤12 这样的式子都是一元一次不等式.
一元一次不等式的概念
我们把含有一个未知数,并且未知数的次数都是1的不等式叫做一元一次不等式.
三、自主学习
1.下列不等式中,哪些是一元一次不等式
(1) 3x+2>x–1 (2)5x+3<0
(3) (4) x2-x–<2x
√
√
×
×
未知数次数不是1
未知数次数超过了1
练一练
四、合作探究
探究一 用数轴表示不等式的解集
0
1
2
3
4
5
6
-1
0
1
2
3
4
5
6
-1
0
1
2
3
4
5
6
-1
0
1
2
3
4
5
6
-1
x>2
x<2
x .
x .
>3
<3
观察解集在数轴上表示方式并填空.
大于向 画;
小于向 画.
小结:
右
左
四、合作探究
0
1
2
3
4
5
6
-1
0
1
2
3
4
5
6
-1
x>2
x≥2
0
1
2
3
4
5
6
-1
0
1
2
3
4
5
6
-1
x .
x .
≥3
≤3
>、<画 圆;
≥、≤画 圆.
小结:
x≥2包括2,所以把表示2的点画成实心点.
空心
实心
四、合作探究
练一练
1.利用数轴来表示下列不等式的解集.
(1) x≥- 3; (2) x < .
解:
-2
-3
(1)
-1
0
0
1
(2)
2
四、合作探究
问题提出:试着求出不等式7 + 5x ≤12的解集,并用数轴表示.
问题探究:首先可以先将不等式转化成mx≤n的形式,
利用不等式的性质1.两边同时减去 ,得 .
7
5x≤5
这一步骤相当于把不等式左边的7移到不等式右边,类似于解方程中的移项.
下一步就能由5x≤5得到x≤1.
再利用 .两边同时除以 ,得出解集.
不等式的性质2
5
探究二 解一元一次不等式
四、合作探究
探究二 解一元一次不等式
问题提出:试着求出不等式7 + 5x ≤12的解集,并用数轴表示.
问题解决:
7+5x≤12
5x≤5
x≤1
用数轴表示:
2
1
0
四、合作探究
练一练
2.解下列不等式,并把它们解集在数轴上表示出来:
2x+2<6
2x<4
x<2
解集在数轴上表示:
解:
(1) 2x+2<6
(2) -3x>
0
1
2
解集在数轴上表示:
解:
-2
-1
0
-3x>
x<
五、当堂检测
1.解下列不等式,并把它们解集在数轴上表示出来:
x+5>-x
2x>-5
解集在数轴上表示:
解:
(1) x+5>-x
(2) <1
解集在数轴上表示:
解:
<1
1-x<4
x>
x>-3
-3
-2
-1
0
-3
-2
-1
0
五、当堂检测
2.写出下列数轴上所有表示的不等式的解集:
0
1
2
-1
-3
0
2
-4
(1)
(2)
-1
-2
1
3
解:x<1.5
解:x≥-3
1.5
五、当堂检测
3.已知关于x的不等式x<a+1的解集与不等式 <-1的解集完全相同,求a的值.
x<-2
两个不等式的解集相同
所以 a+1=-2
a=-3
解: <-1
六、课堂总结
解一元一次不等式
不等式的解与解集
在数轴上
表示不等式
能使含未知数的不等式成立的未知数的值叫___________.
一个含未知数的不等式的所有解组成这个不等式的_____.
求解不等式解集的过程,叫做____________.
方向:大于向____,小于向____
边界:________包含边界,
________不包含边界.
一元一次
不等式
含有 未知数.
未知数的次数为_____.
不等式的解
解集
解不等式
右
左
实心点
空心圆圈
一个
一次
10.3 解一元一次不等式
第1课时
第十章 一元一次不等式和一元一次不等式组
学习导航
学习目标
新课导入
自主学习
合作探究
当堂检测
课堂总结
一、学习目标
1.知道不等式的解、不等式的解集、解不等式等、一元一次不等式概念;
2.会解简单的不等式,并能用数轴正确表示不等式的解集.
二、新课导入
上节课学习的不等式的基本性质有哪些?
根据不等式的基本性质,怎么解一元一次不等式呢?
不等式的性质1:如果 a > b,那么 a ± c > b ± c,
不等式的性质2:如果a>b,c>0,那么 ac>bc,
不等式的性质3:如果a > b,c < 0,那么 ac < bc.
问题1:下面给出的数中,能使不等式x>50成立吗?
知识点一: 不等式的解与解集
20, 40, 50, 100.
解:当x=20,20<50,不成立;
当x=100,100>50,成立.
当x=50,50=50,不成立;
当x=40,40<50,不成立;
归纳总结:
对于含有未知数的不等式,能使不等式成立的未知数的值,叫做不等式的解.
三、自主学习
问题2:(1)你能判断下列哪些数字是不等式 的解吗?
三、自主学习
60,73,74.9,75.1,76,79,80,90.
x 60 73 74.9 75.1 76 79 80 90
不是
是
是
不是
不是
是
是
是
100;153;168....
(2)你还能找出这个不等式的其他解吗?这个不等式有多少个解?
不等式的解有无数个.
问题2:(3)你发现了哪些数是这个不等式的解?你从表格中发现了什么规律?
一般的,一个含有未知数的不等式的所有的解组成这个不等式的解集.
三、自主学习
只要x的值大于75就是这个不等式的解.
求不等式的解集的过程叫做解不等式.
x 60 73 74.9 75.1 76 79 80 90
不是
是
是
不是
不是
是
是
是
问题3:如果要写出不等式的所有解,该如何表示呢?
0
75
例:x>75的解集为:
三、自主学习
第一种:用式子,
即用最简形式的不等式(如x>a或x
第二种:用数轴,
一般标出数轴上某一区间,其中的点对应的数值都是不等式的解.
注意:空心圆圈表示不包含这一点.
不等式的解 不等式的解集
区别 定义
特点
形式
联系
满足一个不等式的未知数
的某个值
满足一个不等式的未知数的所有值
个体
全体
x = 0.9 是 7 + 5x< 12的一个解
x < 1 是 7 + 5x < 12 的 解集
某个解一定是解集中的一员
解集一定包括了某个解
问题4:不等式的解和解集有什么区别与联系呢?
三、自主学习
问题:什么是一元一次方程?
三、自主学习
只含一个未知数、未知数的次数都是1且两边都是整式的等式.
思考:根据一元一次方程的定义,你能猜出一元一次不等式的定义吗?
含有 ,并且 的不等式叫做一元一次不等式.
一个未知数
未知数的次数都是1
知识点二: 一元一次不等式
三、自主学习
像x>3,y≤0,7 + 5x ≤12 这样的式子都是一元一次不等式.
一元一次不等式的概念
我们把含有一个未知数,并且未知数的次数都是1的不等式叫做一元一次不等式.
三、自主学习
1.下列不等式中,哪些是一元一次不等式
(1) 3x+2>x–1 (2)5x+3<0
(3) (4) x2-x–<2x
√
√
×
×
未知数次数不是1
未知数次数超过了1
练一练
四、合作探究
探究一 用数轴表示不等式的解集
0
1
2
3
4
5
6
-1
0
1
2
3
4
5
6
-1
0
1
2
3
4
5
6
-1
0
1
2
3
4
5
6
-1
x>2
x<2
x .
x .
>3
<3
观察解集在数轴上表示方式并填空.
大于向 画;
小于向 画.
小结:
右
左
四、合作探究
0
1
2
3
4
5
6
-1
0
1
2
3
4
5
6
-1
x>2
x≥2
0
1
2
3
4
5
6
-1
0
1
2
3
4
5
6
-1
x .
x .
≥3
≤3
>、<画 圆;
≥、≤画 圆.
小结:
x≥2包括2,所以把表示2的点画成实心点.
空心
实心
四、合作探究
练一练
1.利用数轴来表示下列不等式的解集.
(1) x≥- 3; (2) x < .
解:
-2
-3
(1)
-1
0
0
1
(2)
2
四、合作探究
问题提出:试着求出不等式7 + 5x ≤12的解集,并用数轴表示.
问题探究:首先可以先将不等式转化成mx≤n的形式,
利用不等式的性质1.两边同时减去 ,得 .
7
5x≤5
这一步骤相当于把不等式左边的7移到不等式右边,类似于解方程中的移项.
下一步就能由5x≤5得到x≤1.
再利用 .两边同时除以 ,得出解集.
不等式的性质2
5
探究二 解一元一次不等式
四、合作探究
探究二 解一元一次不等式
问题提出:试着求出不等式7 + 5x ≤12的解集,并用数轴表示.
问题解决:
7+5x≤12
5x≤5
x≤1
用数轴表示:
2
1
0
四、合作探究
练一练
2.解下列不等式,并把它们解集在数轴上表示出来:
2x+2<6
2x<4
x<2
解集在数轴上表示:
解:
(1) 2x+2<6
(2) -3x>
0
1
2
解集在数轴上表示:
解:
-2
-1
0
-3x>
x<
五、当堂检测
1.解下列不等式,并把它们解集在数轴上表示出来:
x+5>-x
2x>-5
解集在数轴上表示:
解:
(1) x+5>-x
(2) <1
解集在数轴上表示:
解:
<1
1-x<4
x>
x>-3
-3
-2
-1
0
-3
-2
-1
0
五、当堂检测
2.写出下列数轴上所有表示的不等式的解集:
0
1
2
-1
-3
0
2
-4
(1)
(2)
-1
-2
1
3
解:x<1.5
解:x≥-3
1.5
五、当堂检测
3.已知关于x的不等式x<a+1的解集与不等式 <-1的解集完全相同,求a的值.
x<-2
两个不等式的解集相同
所以 a+1=-2
a=-3
解: <-1
六、课堂总结
解一元一次不等式
不等式的解与解集
在数轴上
表示不等式
能使含未知数的不等式成立的未知数的值叫___________.
一个含未知数的不等式的所有解组成这个不等式的_____.
求解不等式解集的过程,叫做____________.
方向:大于向____,小于向____
边界:________包含边界,
________不包含边界.
一元一次
不等式
含有 未知数.
未知数的次数为_____.
不等式的解
解集
解不等式
右
左
实心点
空心圆圈
一个
一次
同课章节目录
- 第六章 二元一次方程组
- 6.1 二元一次方程组
- 6.2 二元一次方程组的解法
- 6.3 二元一次方程组的应用
- 6.4 简单的三元一次方程组
- 第七章 相交线与平行线
- 7.1 命题
- 7.2 相交线
- 7.3 平行线
- 7.4 平行线的判定
- 7.5 平行线的性质
- 7.6 图形的平移
- 第八章 整式乘法
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 8.4 整式的乘法
- 8.5 乘法公式
- 第九章 三角形
- 9.1 三角形的边
- 9.2 三角形的内角
- 9.3 三角形的角平分线、中线和高
- 第十章 一元一次不等式和一元一次不等式组
- 10.1 不等式
- 10.2 不等式的基本性质
- 10.3 解一元一次不等式
- 10.4 一元一次不等式的应用
- 10.5 一元一次不等式组
- 第十一章 因式分解
- 11.1 因式分解
- 11.2 提公因式法
- 11.3 公式法
