6.1.2 平行四边形对角线的性质 课件(共19张PPT)
文档属性
| 名称 | 6.1.2 平行四边形对角线的性质 课件(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 714.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 08:36:00 | ||
图片预览





文档简介
(共19张PPT)
第6章 平行四边形
6.1 平行四边形的性质
第2课时 平行四边形对角线的性质
1.掌握平行四边形对角线互相平分的性质,学会应用平行四边形的性质.
2.学生通过观察分析,得出平行四边形对角线的性质
1.平行四边形性质的应用
2.发展合情推理及逻辑推理能力
教学目标
重难点
导入新课
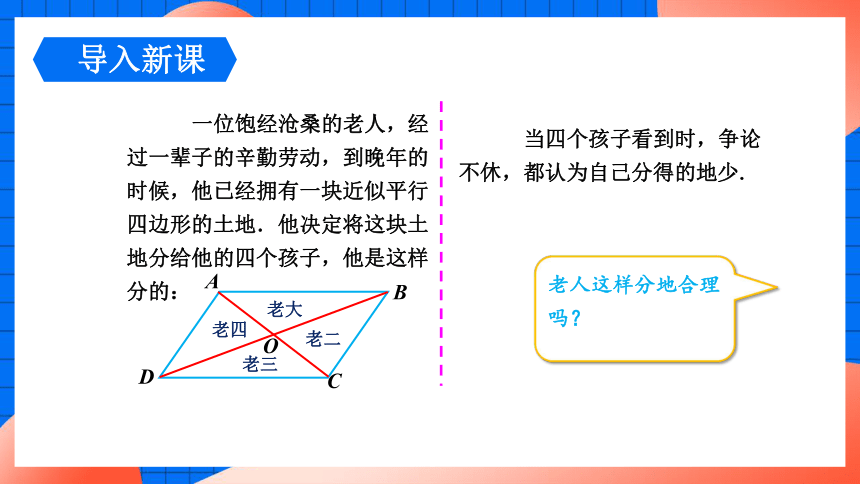
一位饱经沧桑的老人,经过一辈子的辛勤劳动,到晚年的时候,他已经拥有一块近似平行四边形的土地.他决定将这块土地分给他的四个孩子,他是这样分的:
当四个孩子看到时,争论不休,都认为自己分得的地少.
A
B
C
D
O
老大
老二
老三
老四
老人这样分地合理吗?
复习导入
1.对边相等
2.对角相等
A
B
D
C
O
上节课我们学行四边形的两个性质:
复习导入
●
A
D
O
C
B
D
B
O
C
A
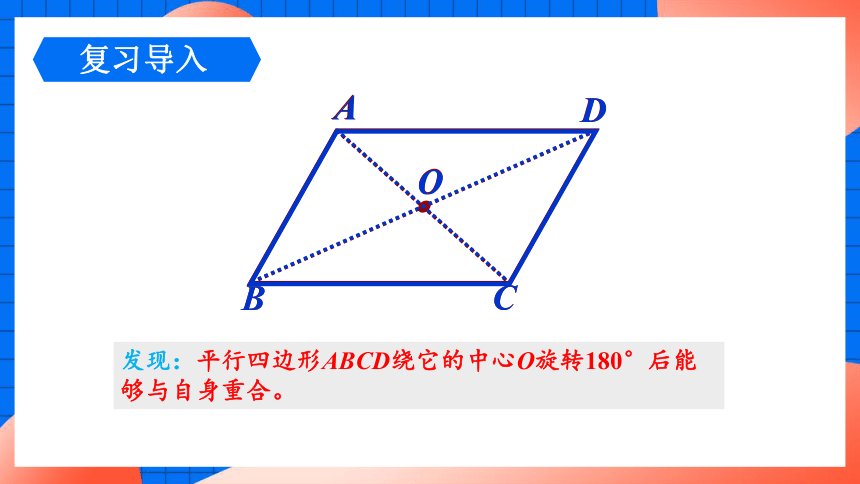
发现:平行四边形ABCD绕它的中心O旋转180°后能够与自身重合。
你能证明它吗
(1)平行四边形是中心对称图形,两条对角线的交点是对称中心;
(2)平行四边形的对角线互相平分.
归纳新知
探究新知
已知:如图,□ABCD 的对角线 AC,BD 相交于点 O. 求证:OA = OC,OB = OD.
证明:
∵ 四边形 ABCD 是平行四边形,
∴ AD = BC,AD∥BC.
∴ ∠1=∠2,∠3=∠4.
∴△AOD≌△COB(ASA).
∴ OA=OC,OB=OD.
A
C
D
B
O
3
2
4
1
归纳新知
A
C
D
B
O
平行四边形的对角线互相平分.
平行四边形的性质
几何语言:
∵□ABCD 的对角线 AC,BD 相交于点 O,
∴ OA = OC,OB = OD.
探究新知
A
C
D
B
O
●
四块地谁大谁小呢?
其实四块地一样大.
典型例题
例1 已知:如图, ABCD的对角线AC与BD相交于点O,过点O的直线与AD,BC分别相交于点E,F.
求证:OE=OF.
典型例题
证明:∵四边形ABCD是平行四边形,
∴DO=BO(平行四边形的对角线互相平分),
AD∥BC(平行四边形的定义).
∴∠ODE=∠OBF,
∵ ∠DOE=∠BOF.
∴△DOE≌△BOF.
∴OE=OF.
典型例题
【方法指导】平行四边形的对边相等,可得到AB+AD=30 cm,由平行四边形的对角线互相平分可得到OB=OD,△AOB的周长比△DOA的周长长5 cm,
例2.已知 ABCD的周长为60 cm,对角线AC,BD相交于点O,△AOB的周长比△DOA的周长长5 cm,求这个平行四边形各边的长.
D
C
B
A
O
实际上就是AB-AD=5 cm,根据AB+AD=30 cm,AB-AD=5 cm,求出 ABCD的各边长.
典型例题
解:∵四边形ABCD是平行四边形,
∴OB=OD,AB=CD,AD=BC.
∵△AOB的周长比△DOA的周长长5 cm,
∴AB-AD=5 cm.
又∵ ABCD的周长为60 cm,
∴AB+AD=30 cm,
∴AB=17.5 cm,AD=12.5 cm,
则AB=CD=17.5 cm,AD=BC=12.5 cm.
D
C
B
A
O
随堂练习
1. 如图,□ ABCD 的对角线 AC、BD 相交于点 O,且 AC + BD = 16,CD = 6,则△ABO 的周长是( )
A. 10 B. 14
C. 20 D. 22
B
B
C
D
A
O
2. 下列性质中,平行四边形不一定具备的是( )
A. 对边相等 B. 对角相等
C. 对角线互相平分 D. 是轴对称图形
D
随堂练习
3.平行四边形两条对角线的长分别为10,16,则它的边长x的取值范围是_________.
4. ABCD的对角线AC、BD相交于点O,且AC+BD=40,AB=13,则△OCD的周长为____.
3<x<13
33
随堂练习
5.如图,在 ABCD中,对角线AC、BD相交于O,AC=6,BD=8,AB=5,
(1)求 ABCD的周长;
(2)求 ABCD的面积.
解:(1)由平行四边形的性质得:
OC=OA= AC=3,OB=OD= BD=4.
在△AOB中,OA2+OB2=32+42=52=AB2.
随堂练习
∴△AOB是直角三角形,∠AOB=90°.
∴AC⊥BD.
(2)由(1)知:AC⊥BD
∴
课后作业
完成教材习题6.2
这节课你学到了什么?谈谈你的收获,
小结与反思
第6章 平行四边形
6.1 平行四边形的性质
第2课时 平行四边形对角线的性质
1.掌握平行四边形对角线互相平分的性质,学会应用平行四边形的性质.
2.学生通过观察分析,得出平行四边形对角线的性质
1.平行四边形性质的应用
2.发展合情推理及逻辑推理能力
教学目标
重难点
导入新课
一位饱经沧桑的老人,经过一辈子的辛勤劳动,到晚年的时候,他已经拥有一块近似平行四边形的土地.他决定将这块土地分给他的四个孩子,他是这样分的:
当四个孩子看到时,争论不休,都认为自己分得的地少.
A
B
C
D
O
老大
老二
老三
老四
老人这样分地合理吗?
复习导入
1.对边相等
2.对角相等
A
B
D
C
O
上节课我们学行四边形的两个性质:
复习导入
●
A
D
O
C
B
D
B
O
C
A
发现:平行四边形ABCD绕它的中心O旋转180°后能够与自身重合。
你能证明它吗
(1)平行四边形是中心对称图形,两条对角线的交点是对称中心;
(2)平行四边形的对角线互相平分.
归纳新知
探究新知
已知:如图,□ABCD 的对角线 AC,BD 相交于点 O. 求证:OA = OC,OB = OD.
证明:
∵ 四边形 ABCD 是平行四边形,
∴ AD = BC,AD∥BC.
∴ ∠1=∠2,∠3=∠4.
∴△AOD≌△COB(ASA).
∴ OA=OC,OB=OD.
A
C
D
B
O
3
2
4
1
归纳新知
A
C
D
B
O
平行四边形的对角线互相平分.
平行四边形的性质
几何语言:
∵□ABCD 的对角线 AC,BD 相交于点 O,
∴ OA = OC,OB = OD.
探究新知
A
C
D
B
O
●
四块地谁大谁小呢?
其实四块地一样大.
典型例题
例1 已知:如图, ABCD的对角线AC与BD相交于点O,过点O的直线与AD,BC分别相交于点E,F.
求证:OE=OF.
典型例题
证明:∵四边形ABCD是平行四边形,
∴DO=BO(平行四边形的对角线互相平分),
AD∥BC(平行四边形的定义).
∴∠ODE=∠OBF,
∵ ∠DOE=∠BOF.
∴△DOE≌△BOF.
∴OE=OF.
典型例题
【方法指导】平行四边形的对边相等,可得到AB+AD=30 cm,由平行四边形的对角线互相平分可得到OB=OD,△AOB的周长比△DOA的周长长5 cm,
例2.已知 ABCD的周长为60 cm,对角线AC,BD相交于点O,△AOB的周长比△DOA的周长长5 cm,求这个平行四边形各边的长.
D
C
B
A
O
实际上就是AB-AD=5 cm,根据AB+AD=30 cm,AB-AD=5 cm,求出 ABCD的各边长.
典型例题
解:∵四边形ABCD是平行四边形,
∴OB=OD,AB=CD,AD=BC.
∵△AOB的周长比△DOA的周长长5 cm,
∴AB-AD=5 cm.
又∵ ABCD的周长为60 cm,
∴AB+AD=30 cm,
∴AB=17.5 cm,AD=12.5 cm,
则AB=CD=17.5 cm,AD=BC=12.5 cm.
D
C
B
A
O
随堂练习
1. 如图,□ ABCD 的对角线 AC、BD 相交于点 O,且 AC + BD = 16,CD = 6,则△ABO 的周长是( )
A. 10 B. 14
C. 20 D. 22
B
B
C
D
A
O
2. 下列性质中,平行四边形不一定具备的是( )
A. 对边相等 B. 对角相等
C. 对角线互相平分 D. 是轴对称图形
D
随堂练习
3.平行四边形两条对角线的长分别为10,16,则它的边长x的取值范围是_________.
4. ABCD的对角线AC、BD相交于点O,且AC+BD=40,AB=13,则△OCD的周长为____.
3<x<13
33
随堂练习
5.如图,在 ABCD中,对角线AC、BD相交于O,AC=6,BD=8,AB=5,
(1)求 ABCD的周长;
(2)求 ABCD的面积.
解:(1)由平行四边形的性质得:
OC=OA= AC=3,OB=OD= BD=4.
在△AOB中,OA2+OB2=32+42=52=AB2.
随堂练习
∴△AOB是直角三角形,∠AOB=90°.
∴AC⊥BD.
(2)由(1)知:AC⊥BD
∴
课后作业
完成教材习题6.2
这节课你学到了什么?谈谈你的收获,
小结与反思
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
