7.1.1三角形的边
图片预览



文档简介
课件28张PPT。第七章 三角形三角形的边引入 欣赏图片引 入ABC三角形想一想:什么叫三角形?新授 ABC三角形的定义:由不在同一直线上的
三条线段首位顺次相接所组成的图形
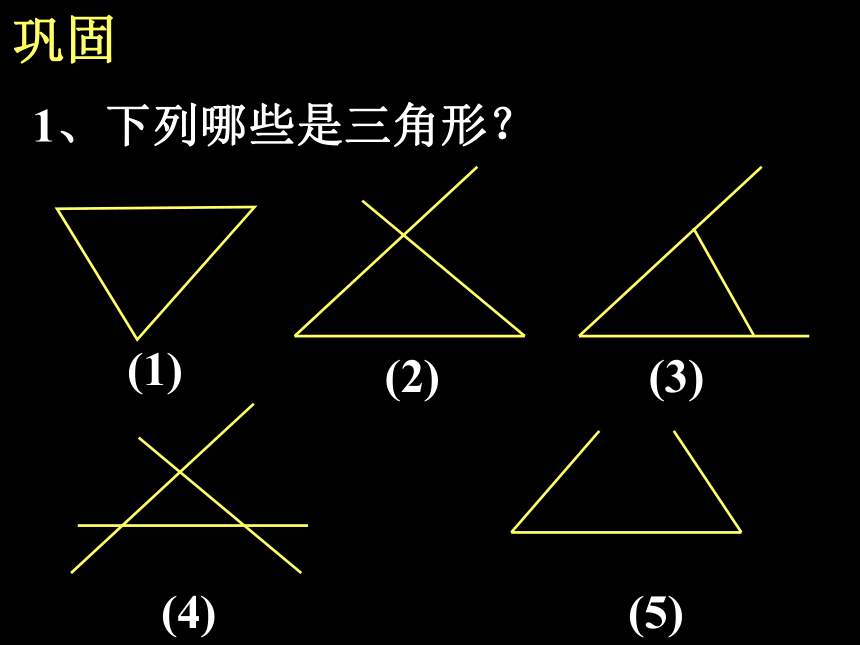
叫三角形 巩固1、下列哪些是三角形?(1)(2)(3)(4)(5)新授认识三角形ABC2、线段AB、BC、CD
分别是三角形的边。1、点A、B、C
分别是三角形的顶点。3、∠A、 ∠B、 ∠C
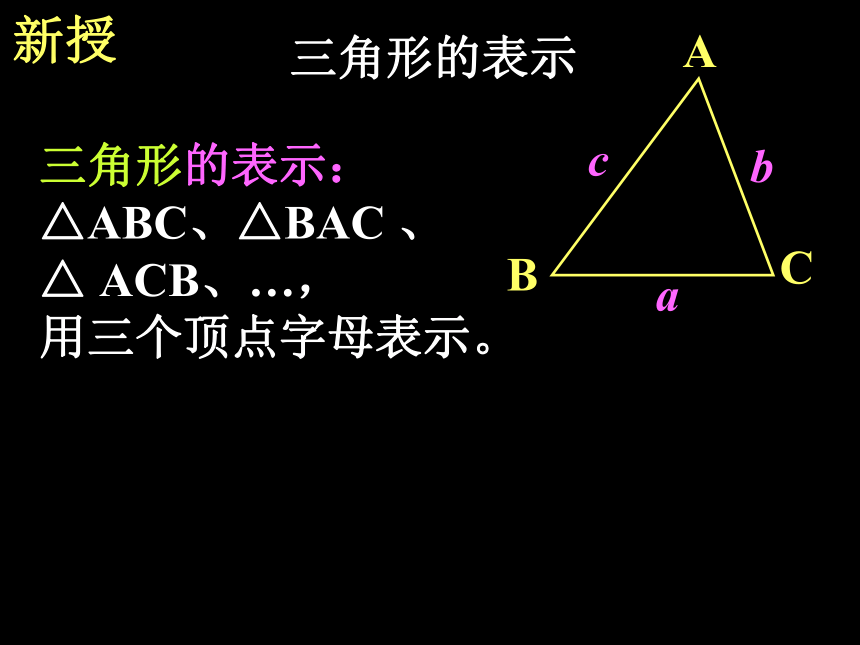
分别是三角形的内角,简称角。新授三角形的表示ABC三角形的表示:
△ABC、△BAC 、
△ ACB、…,
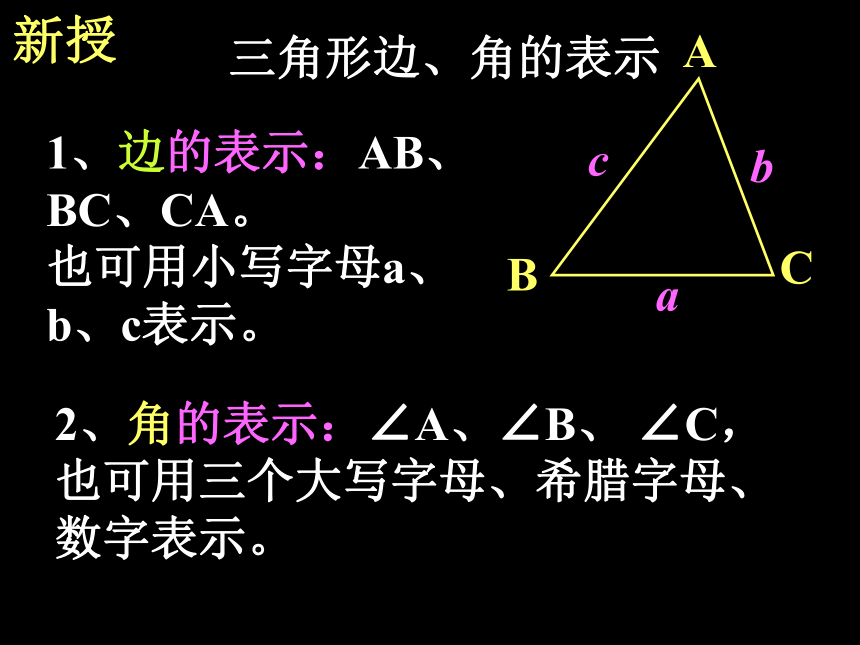
用三个顶点字母表示。cab新授三角形边、角的表示ABC1、边的表示:AB、
BC、CA。
也可用小写字母a、
b、c表示。2、角的表示:∠A、∠B、 ∠C,
也可用三个大写字母、希腊字母、
数字表示。cab探究观察下列三角形,你有什么发现?归纳三角形不等边三角形等腰三角形底和腰不相等
的等腰三角形底和腰相等的 等边三角形三角形按边分类探究观察下列三角形,你有什么发现?归纳三角形直角三角形斜三角形锐角三角形钝角三角形三角形按角分类巩固(2)三角形按边分为两类:分别是
等腰三角形和不等边三角形。3、判断下列说法是否正确:(1)三角形按边分为两类:分别是
等腰三角形和等边三角形。探究蚂蚁要从A点去B点觅食,请你帮忙
设计一条线路。ABC你有什么新发现吗?归纳三角形三边关系定理:三角形任意
两边之和大于第三边。ABCcab如:AB+BC>CAa+b>c三角形三边关系定理:三角形任意
两边之差小于第三边。如:AB-BC2cm,它们能否围成三角形?为什么?你有什么更好的办法吗?用两条小边之和与大边比较用最大边减中边之差与最小边比较巩固4、下列长度的三条线段能否组成三角
形?为什么?
(1) 3cm、4cm、8cm
(2) 5、11、6
(3) 6︰10︰5巩固5、在△ABC中,若a =3,b=7,则第
三边c的取值范围是 。既要考虑“两边之和大于第三边”,
又要考虑“两边之差小于第三边”a - b < c < a + b在△ABC中,若a =3,b=7,则其周
长l的取值范围是 。范例例2、等腰三角形两边长分别为3cm和
4cm,求三角形的周长。分类思想:见有关“等腰三角形的边”
的问题,就考虑腰和底的分类。巩固7、等腰三角形的周长是14,其中一
边长是4cm,求另外两边边长。8、等腰三角形的周长是14,其中一
边长是8cm,求另外两边边长。6、等腰三角形两边长分别为3cm和
6cm,求三角形的周长。小结三角形定义表示方法三边关
系定理分类按边分类按角分类a - b < c < a + b作业2、等腰三角形的周长是32cm,腰长
的3倍比底边长的2倍多6cm,求各边
边长。1、五条长度分别是2、3、4、5、6
的线段,任选三条可以组成多少个
三角形?它们的边长分别是多少?1.图中有几个三角形?用符号表示这些三角形。2.以AB为边的三角形有哪些?△ABC、△ABE3.以E为顶点的三角形有哪些?△ ABE 、△BCE、 △CDE小试牛刀4.以∠D为角的三角形有哪些?△ BCD、 △DEC只要满足较小的两条线段之和大于第三条线段,便可构成三角形;若不满足,则不能构成三角形.下列长度的各组线段能否组成一个三角形?
(1)15cm、10cm、7cm (2) 4cm、5cm、10cm
(3) 3cm、8cm、5cm (4) 4cm、5cm、6cm练一练较小两边之和大于第三边,才能构成三角形1.下列长度的三条线段能否组成三角形?为什么?(1) 3,4,8 ( )
(2) 2,5,6 ( )
(3) 5,6,10 ( )
(4) 2,5,8 ( )不能能能不能再练一练1、已知两条线段的长分别是3cm、5cm ,
要想拼成一个三角形,问第三条线段a应
取的范围是多少? 试一试 2、已知两条线段的长分别是3cm、5cm ,
要想拼成一个三角形,且第三条线段a的
长为奇数,问第三条线段应取多少长? 2cm两边之差<第三边<两边之和2、已知两条边长分别为2cm、5cm,
你可以画出几个符合条件的等腰三角形?做一做1、已知两条边长分别为3cm、5cm,你可以
画出几个符合条件的等腰三角形?并求符合
条件的等腰三角形的周长. 用长度分别为7cm、8cm、12cm、16cm的四根木棒,取其中三根搭成三角形。哪些能,哪些不能?你能搭成几个三角形?
7cm8cm12cm7cm8cm16cm7cm12cm16cm8cm12cm16cm能你发现三角形的边之间有何关系?能能不能探究
三条线段首位顺次相接所组成的图形
叫三角形 巩固1、下列哪些是三角形?(1)(2)(3)(4)(5)新授认识三角形ABC2、线段AB、BC、CD
分别是三角形的边。1、点A、B、C
分别是三角形的顶点。3、∠A、 ∠B、 ∠C
分别是三角形的内角,简称角。新授三角形的表示ABC三角形的表示:
△ABC、△BAC 、
△ ACB、…,
用三个顶点字母表示。cab新授三角形边、角的表示ABC1、边的表示:AB、
BC、CA。
也可用小写字母a、
b、c表示。2、角的表示:∠A、∠B、 ∠C,
也可用三个大写字母、希腊字母、
数字表示。cab探究观察下列三角形,你有什么发现?归纳三角形不等边三角形等腰三角形底和腰不相等
的等腰三角形底和腰相等的 等边三角形三角形按边分类探究观察下列三角形,你有什么发现?归纳三角形直角三角形斜三角形锐角三角形钝角三角形三角形按角分类巩固(2)三角形按边分为两类:分别是
等腰三角形和不等边三角形。3、判断下列说法是否正确:(1)三角形按边分为两类:分别是
等腰三角形和等边三角形。探究蚂蚁要从A点去B点觅食,请你帮忙
设计一条线路。ABC你有什么新发现吗?归纳三角形三边关系定理:三角形任意
两边之和大于第三边。ABCcab如:AB+BC>CAa+b>c三角形三边关系定理:三角形任意
两边之差小于第三边。如:AB-BC
形?为什么?
(1) 3cm、4cm、8cm
(2) 5、11、6
(3) 6︰10︰5巩固5、在△ABC中,若a =3,b=7,则第
三边c的取值范围是 。既要考虑“两边之和大于第三边”,
又要考虑“两边之差小于第三边”a - b < c < a + b在△ABC中,若a =3,b=7,则其周
长l的取值范围是 。范例例2、等腰三角形两边长分别为3cm和
4cm,求三角形的周长。分类思想:见有关“等腰三角形的边”
的问题,就考虑腰和底的分类。巩固7、等腰三角形的周长是14,其中一
边长是4cm,求另外两边边长。8、等腰三角形的周长是14,其中一
边长是8cm,求另外两边边长。6、等腰三角形两边长分别为3cm和
6cm,求三角形的周长。小结三角形定义表示方法三边关
系定理分类按边分类按角分类a - b < c < a + b作业2、等腰三角形的周长是32cm,腰长
的3倍比底边长的2倍多6cm,求各边
边长。1、五条长度分别是2、3、4、5、6
的线段,任选三条可以组成多少个
三角形?它们的边长分别是多少?1.图中有几个三角形?用符号表示这些三角形。2.以AB为边的三角形有哪些?△ABC、△ABE3.以E为顶点的三角形有哪些?△ ABE 、△BCE、 △CDE小试牛刀4.以∠D为角的三角形有哪些?△ BCD、 △DEC只要满足较小的两条线段之和大于第三条线段,便可构成三角形;若不满足,则不能构成三角形.下列长度的各组线段能否组成一个三角形?
(1)15cm、10cm、7cm (2) 4cm、5cm、10cm
(3) 3cm、8cm、5cm (4) 4cm、5cm、6cm练一练较小两边之和大于第三边,才能构成三角形1.下列长度的三条线段能否组成三角形?为什么?(1) 3,4,8 ( )
(2) 2,5,6 ( )
(3) 5,6,10 ( )
(4) 2,5,8 ( )不能能能不能再练一练1、已知两条线段的长分别是3cm、5cm ,
要想拼成一个三角形,问第三条线段a应
取的范围是多少? 试一试 2、已知两条线段的长分别是3cm、5cm ,
要想拼成一个三角形,且第三条线段a的
长为奇数,问第三条线段应取多少长? 2cm
你可以画出几个符合条件的等腰三角形?做一做1、已知两条边长分别为3cm、5cm,你可以
画出几个符合条件的等腰三角形?并求符合
条件的等腰三角形的周长. 用长度分别为7cm、8cm、12cm、16cm的四根木棒,取其中三根搭成三角形。哪些能,哪些不能?你能搭成几个三角形?
7cm8cm12cm7cm8cm16cm7cm12cm16cm8cm12cm16cm能你发现三角形的边之间有何关系?能能不能探究
