20.2 函数( 第1课时) 课件 17张PPT 冀教版数学八年级下册
文档属性
| 名称 | 20.2 函数( 第1课时) 课件 17张PPT 冀教版数学八年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 360.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-18 21:27:55 | ||
图片预览






文档简介
(共17张PPT)
第二十章 函数
20.2 函数
第1课时
1.了解函数的相关概念,会判断两个变量是否具有函数关系.
2.能根据简单的实际问题写出函数解析式.
3.会根据函数解析式求函数值.
合作探究
当堂检测
学习目标
课堂总结
自主学习
这里有变化的量吗?
如果有,是什么?
它们之间有关系吗?
游戏:数青蛙
一只青蛙一张嘴,两只眼睛四条腿;
两只青蛙两张嘴,四只眼睛八条腿;
三只青蛙三张嘴,六只眼睛十二条腿.
1.青蛙的眼睛数和只数有关系吗?能用数学式表达吗?
2.青蛙的腿数和只数有关系吗?能用数学式表达吗?
合作探究
当堂检测
学习目标
课堂总结
自主学习
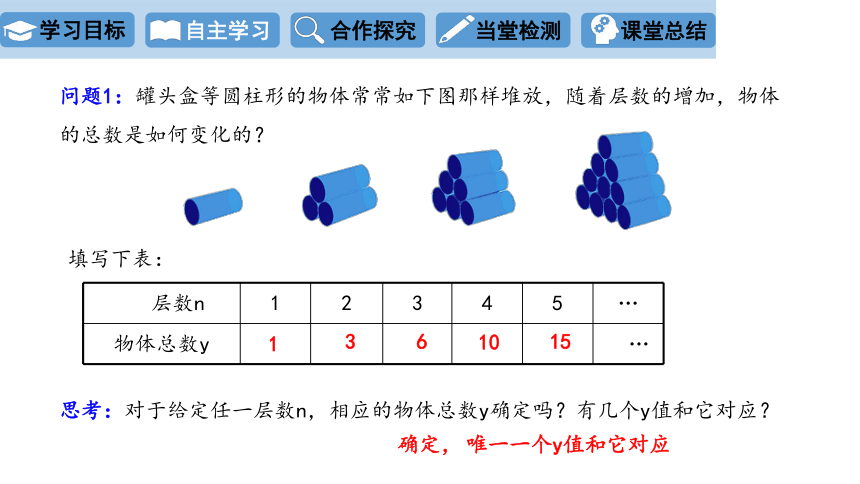
问题1:罐头盒等圆柱形的物体常常如下图那样堆放,随着层数的增加,物体的总数是如何变化的?
填写下表:
层数n 1 2 3 4 5 …
物体总数y …
1
3
6
10
15
思考:对于给定任一层数n,相应的物体总数y确定吗?有几个y值和它对应?
唯一一个y值和它对应
确定,
合作探究
当堂检测
学习目标
课堂总结
自主学习
问题2:一定质量的气体在体积不变时,假若温度降低到-273℃,则气体的压强为零.因此,物理学把-273℃作为热力学温度的零度.热力学温度T(K)与摄氏温度t(℃)之间有如下数量关系:T=t+273,T≥0.
(1)当t分别等于-43,-27,0,18时,相应的热力学温度T是多少?
解:当t=-43时,T=-43+273=230(K);
当t=-27时,T=-27+273=246(K);
当t=0时,T=0+273=273(K);
当t=18时,T=18+273=291(K)
(2)给定任一个大于-273 ℃的摄氏温度t值,相应的热力学温度T确定吗?有几个T值和它对应?
唯一一个T值和它对应
确定,
合作探究
当堂检测
学习目标
课堂总结
自主学习
议一议:前面两个问题有什么共同点?
①层数n、物体总数y;
②摄氏温度t 、热力学温度T.
共同特点:都有两个变量,给定其中某一个变量的值,相应地就确定了另一个变量的值.
合作探究
当堂检测
学习目标
课堂总结
自主学习
得出概念:
一般地,在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与它对应,那么我们就说x是自变量,y是x的函数.
如果当x=a时y=b,那么b叫做当自变量的值为a时的函数值.
合作探究
当堂检测
学习目标
课堂总结
自主学习
探究一 判断变量间的函数关系
问题探究:
问题提出:下列关于变量x,y的关系式: y =2x+3; y =x2+3; y =2|x|;④ ;⑤y2-3x=10,其中表示y是x的函数关系的是 .
(1)说一说x和y在什么情况下成函数关系.
对于x的每一个确定的值,y都有唯一确定的值与它对应.
(2)根据这个条件,对你解题有什么启发?
任取x的一个值代入式子,看是否有唯一的一个y值对应.
如果是,则y是x的函数;如果不是,y则不是x的函数.
①②③
合作探究
当堂检测
学习目标
课堂总结
自主学习
方法归纳:
判断一个变量是否是另一个变量的函数,关键是看当一个变量确定时,另一个变量有唯一确定的值与它对应.
合作探究
当堂检测
学习目标
课堂总结
自主学习
练一练
1.在下列关系式中:①长方形的宽一定时,其长与面积的关系;②等腰三角形的底边长与面积;③圆的面积与圆的半径.其中,是函数关系的是
(填序号)
①③
合作探究
当堂检测
学习目标
课堂总结
自主学习
探究二 列函数的解析式
问题提出:公路上依次有A,B,C三个汽车站,上午8时,小明骑自行车从A,B两站之间距离A站8km处出发,向C站匀速前进,他骑车的速度是16.5km/小时,若A,B两站间的路程是26km,B,C两站的路程是15km.
(1)小明所走路程与骑车的时间两个变量中,哪个是自变量?哪个是因变量?
(2)设小明出发x小时后,离A站的路程为y km,请写出y与x之间的关系式.
(3)小明在上午9时是否已经经过了B站?
合作探究
当堂检测
学习目标
课堂总结
自主学习
问题探究:
a.路程与时间之间的关系是:
路程=速度×时间
合作探究
当堂检测
学习目标
课堂总结
自主学习
问题解决:
(1)自变量:骑车的时间
因变量:小明所走的路程
(2)路程=16.5x
∴y=16.5x+8
b.距离与路程的关系是:
距离=路程+初始距离
c.有关骑车时间的等量关系式是:
时间=出发后的时间点-出发时的时间点
(3)由题有:x=9-8=1,
∴y=16.5×1+8=24.5
∵AB两站距离=26 km>24.5 km
∴小明在上午9时没有经过B站
归纳总结:
像y=16.5x+8这样,用关于自变量的数学式子表示函数与自变量之间的关系,是描述函数的常用方法.这种式子叫做函数的解析式.
合作探究
当堂检测
学习目标
课堂总结
自主学习
练一练
2.已知池中有600 m3的水,每小时抽50 m3.
(1)写出剩余水的体积V m3关于时间t h的函数解析式;
(2)8 h后,池中还剩多少水?
(3)多长时间后,池中剩余100 m3的水?
解:(1)V=600﹣50t;
(2)当t=8时,
V=600﹣50×8=200;
故8小时后,池中还剩200 m3水.
合作探究
当堂检测
学习目标
课堂总结
自主学习
(3)当V=100时,根据(1)式解得 t=10,
故10小时后,池中还有100 m3的水.
1.下列各表达式不是表示y是x的函数的是( )
A. B.
C. D.
C
合作探究
当堂检测
学习目标
课堂总结
自主学习
2.一批机器需要零件200个,每天加工20个.若设剩余量为y(个),加工天数为x(天).
(1)求y(个)随x(天)变化的函数表达式;
(2)当剩余零件为120个时,加工了多少天?
解:(1)由剩余量等于总量减加工的量,得:y=-20x+200;
(2)当y=120时,200-20x=120,
解得x=4,
即当剩余零件为120个时,加工了4天.
合作探究
当堂检测
学习目标
课堂总结
自主学习
函 数
概念:函数在某个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与它对应,那么x是自变量,y是x的函数.
函数值
函数的解析式
概念:用关于自变量的数学式子表示函数与自变量之间的关系,是描述函数的常用方法.这种式子叫做函数的解析式.
如果当x=a时y=b,那么b叫做当自变量的值为a时的函数值.
合作探究
当堂检测
学习目标
课堂总结
自主学习
第二十章 函数
20.2 函数
第1课时
1.了解函数的相关概念,会判断两个变量是否具有函数关系.
2.能根据简单的实际问题写出函数解析式.
3.会根据函数解析式求函数值.
合作探究
当堂检测
学习目标
课堂总结
自主学习
这里有变化的量吗?
如果有,是什么?
它们之间有关系吗?
游戏:数青蛙
一只青蛙一张嘴,两只眼睛四条腿;
两只青蛙两张嘴,四只眼睛八条腿;
三只青蛙三张嘴,六只眼睛十二条腿.
1.青蛙的眼睛数和只数有关系吗?能用数学式表达吗?
2.青蛙的腿数和只数有关系吗?能用数学式表达吗?
合作探究
当堂检测
学习目标
课堂总结
自主学习
问题1:罐头盒等圆柱形的物体常常如下图那样堆放,随着层数的增加,物体的总数是如何变化的?
填写下表:
层数n 1 2 3 4 5 …
物体总数y …
1
3
6
10
15
思考:对于给定任一层数n,相应的物体总数y确定吗?有几个y值和它对应?
唯一一个y值和它对应
确定,
合作探究
当堂检测
学习目标
课堂总结
自主学习
问题2:一定质量的气体在体积不变时,假若温度降低到-273℃,则气体的压强为零.因此,物理学把-273℃作为热力学温度的零度.热力学温度T(K)与摄氏温度t(℃)之间有如下数量关系:T=t+273,T≥0.
(1)当t分别等于-43,-27,0,18时,相应的热力学温度T是多少?
解:当t=-43时,T=-43+273=230(K);
当t=-27时,T=-27+273=246(K);
当t=0时,T=0+273=273(K);
当t=18时,T=18+273=291(K)
(2)给定任一个大于-273 ℃的摄氏温度t值,相应的热力学温度T确定吗?有几个T值和它对应?
唯一一个T值和它对应
确定,
合作探究
当堂检测
学习目标
课堂总结
自主学习
议一议:前面两个问题有什么共同点?
①层数n、物体总数y;
②摄氏温度t 、热力学温度T.
共同特点:都有两个变量,给定其中某一个变量的值,相应地就确定了另一个变量的值.
合作探究
当堂检测
学习目标
课堂总结
自主学习
得出概念:
一般地,在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与它对应,那么我们就说x是自变量,y是x的函数.
如果当x=a时y=b,那么b叫做当自变量的值为a时的函数值.
合作探究
当堂检测
学习目标
课堂总结
自主学习
探究一 判断变量间的函数关系
问题探究:
问题提出:下列关于变量x,y的关系式: y =2x+3; y =x2+3; y =2|x|;④ ;⑤y2-3x=10,其中表示y是x的函数关系的是 .
(1)说一说x和y在什么情况下成函数关系.
对于x的每一个确定的值,y都有唯一确定的值与它对应.
(2)根据这个条件,对你解题有什么启发?
任取x的一个值代入式子,看是否有唯一的一个y值对应.
如果是,则y是x的函数;如果不是,y则不是x的函数.
①②③
合作探究
当堂检测
学习目标
课堂总结
自主学习
方法归纳:
判断一个变量是否是另一个变量的函数,关键是看当一个变量确定时,另一个变量有唯一确定的值与它对应.
合作探究
当堂检测
学习目标
课堂总结
自主学习
练一练
1.在下列关系式中:①长方形的宽一定时,其长与面积的关系;②等腰三角形的底边长与面积;③圆的面积与圆的半径.其中,是函数关系的是
(填序号)
①③
合作探究
当堂检测
学习目标
课堂总结
自主学习
探究二 列函数的解析式
问题提出:公路上依次有A,B,C三个汽车站,上午8时,小明骑自行车从A,B两站之间距离A站8km处出发,向C站匀速前进,他骑车的速度是16.5km/小时,若A,B两站间的路程是26km,B,C两站的路程是15km.
(1)小明所走路程与骑车的时间两个变量中,哪个是自变量?哪个是因变量?
(2)设小明出发x小时后,离A站的路程为y km,请写出y与x之间的关系式.
(3)小明在上午9时是否已经经过了B站?
合作探究
当堂检测
学习目标
课堂总结
自主学习
问题探究:
a.路程与时间之间的关系是:
路程=速度×时间
合作探究
当堂检测
学习目标
课堂总结
自主学习
问题解决:
(1)自变量:骑车的时间
因变量:小明所走的路程
(2)路程=16.5x
∴y=16.5x+8
b.距离与路程的关系是:
距离=路程+初始距离
c.有关骑车时间的等量关系式是:
时间=出发后的时间点-出发时的时间点
(3)由题有:x=9-8=1,
∴y=16.5×1+8=24.5
∵AB两站距离=26 km>24.5 km
∴小明在上午9时没有经过B站
归纳总结:
像y=16.5x+8这样,用关于自变量的数学式子表示函数与自变量之间的关系,是描述函数的常用方法.这种式子叫做函数的解析式.
合作探究
当堂检测
学习目标
课堂总结
自主学习
练一练
2.已知池中有600 m3的水,每小时抽50 m3.
(1)写出剩余水的体积V m3关于时间t h的函数解析式;
(2)8 h后,池中还剩多少水?
(3)多长时间后,池中剩余100 m3的水?
解:(1)V=600﹣50t;
(2)当t=8时,
V=600﹣50×8=200;
故8小时后,池中还剩200 m3水.
合作探究
当堂检测
学习目标
课堂总结
自主学习
(3)当V=100时,根据(1)式解得 t=10,
故10小时后,池中还有100 m3的水.
1.下列各表达式不是表示y是x的函数的是( )
A. B.
C. D.
C
合作探究
当堂检测
学习目标
课堂总结
自主学习
2.一批机器需要零件200个,每天加工20个.若设剩余量为y(个),加工天数为x(天).
(1)求y(个)随x(天)变化的函数表达式;
(2)当剩余零件为120个时,加工了多少天?
解:(1)由剩余量等于总量减加工的量,得:y=-20x+200;
(2)当y=120时,200-20x=120,
解得x=4,
即当剩余零件为120个时,加工了4天.
合作探究
当堂检测
学习目标
课堂总结
自主学习
函 数
概念:函数在某个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有唯一确定的值与它对应,那么x是自变量,y是x的函数.
函数值
函数的解析式
概念:用关于自变量的数学式子表示函数与自变量之间的关系,是描述函数的常用方法.这种式子叫做函数的解析式.
如果当x=a时y=b,那么b叫做当自变量的值为a时的函数值.
合作探究
当堂检测
学习目标
课堂总结
自主学习
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
