21.4 一次函数的应用( 第1课时 )课件 18张PPT 冀教版八年级数学下册
文档属性
| 名称 | 21.4 一次函数的应用( 第1课时 )课件 18张PPT 冀教版八年级数学下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 260.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-18 21:31:33 | ||
图片预览






文档简介
(共18张PPT)
第二十一章 一次函数
21.4 一次函数的应用
第1课时
1.会根据问题情境的数量关系建立相应的一次函数表达式.
2. 掌握单个一次函数的应用.
合作探究
当堂检测
学习目标
课堂总结
探究 利用一次函数解决简单的实际问题
问题提出1:某公司与销售人员签订了这样的工资合同:工资由两部分组成,一部分是基本工资,每人每月3000元;另一部分是按月销售量确定的奖励工资,每销售1件产品,奖励工资10元.要使月工资超过4500元,该月的销售量应当超过多少件?
问题探究:
a.设某销售员销售产品x件,他应得的工资记为y元.列y与x之间的函数关系式.
y=10x+3000
合作探究
当堂检测
学习目标
课堂总结
问题探究:
b.工资超过4500元,该月的销售量应当超过多少件?
10x+3000>4500
解得x>150
要使月工资超过4500元,该月的销售量应当超过150件.
问题解决:
合作探究
当堂检测
学习目标
课堂总结
练一练
1.客运公司规定旅客可免费携带一定质量的行李,当行李质量超过规定时,需付的行李费y(元)是行李质量x(kg)的一次函数,这个函数的图象如图所示.
(1)求y关于x的函数表达式;
(2)某旅客携带25kg的行李时,需要支付多少行李费?
解:(1)设y与x的函数表达式为y=kx+b,
由题意可得:
解得: ,
当y=0时,解得x=10,
合作探究
当堂检测
学习目标
课堂总结
∴ ,
∴ (x≥10).
练一练
1.客运公司规定旅客可免费携带一定质量的行李,当行李质量超过规定时,需付的行李费y(元)是行李质量x(kg)的一次函数,这个函数的图象如图所示.
(2)某旅客携带25kg的行李时,需要支付多少行李费?
故这位旅客需要支付3元行李费.
合作探究
当堂检测
学习目标
课堂总结
(2)当x=25时,y= (元)
探究 利用一次函数解决简单的实际问题
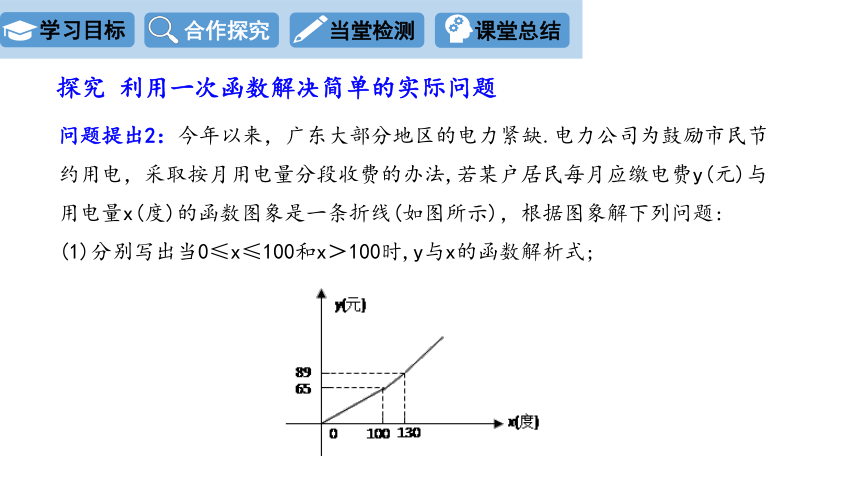
问题提出2:今年以来,广东大部分地区的电力紧缺.电力公司为鼓励市民节约用电,采取按月用电量分段收费的办法,若某户居民每月应缴电费y(元)与用电量x(度)的函数图象是一条折线(如图所示),根据图象解下列问题:
(1)分别写出当0≤x≤100和x>100时,y与x的函数解析式;
合作探究
当堂检测
学习目标
课堂总结
问题探究:
a.当0≤x≤100和x>100时,图象分别经过哪几个点?
当0≤x≤100时,图象经过点(0,0)和(100,65);
当x>100时,图象经过点(100,65)和(130,89).
b.根据上面的已知条件,对你解题有什么启发?
因为函数图象是一条折线,所以解析式要分段讨论,
再根据已知的区间经过的两点,利用待定系数法分别求出每个区间的函数解析式.
合作探究
当堂检测
学习目标
课堂总结
问题解决:
解:设y关于x的函数关系式为y=kx+b,
当0≤x≤100时,将(0,0),(100,65)代入y=kx+b中,
解得: ,
∴y=0.65x(0≤x≤100);
当x>100时,将(100,65),(130,89)代入y=kx+b中,
解得: ,
∴y=0.8x-15(x>100),
y与x的函数解析式也可合起来表示为:
y=
0.65x(0≤x≤100)
0.8x-15(x>100)
{
合作探究
当堂检测
学习目标
课堂总结
探究 利用一次函数解决简单的实际问题
问题提出2:(2)若该用户某月用电62度 ,则应缴费多少元
解:∵62<100,
∴62×0.65
=40.3(元)
答:应缴费40.3元.
a.用电62度是函数解析式中哪个未知数的值?
问题探究:
x
b.应代入哪个解析式求出缴应缴费的多少呢?说说你的理由.
因为62小于100,所以应代入函数y=0.65求出y的值.
问题解决:
合作探究
当堂检测
学习目标
课堂总结
在自变量的不同取值范围内表示函数关系的表达式有不同的形式,这样的函数称为分段函数,分段函数在生活中也有很多应用.
总结归纳
合作探究
当堂检测
学习目标
课堂总结
练一练
2.某校为学生装一台直饮水器,课间学生到直饮水器打水.他们先同时打开全部的水笼头放水,后来又关闭了部分水笼头.假设前后两人接水间隔时间忽略不计,且不发生泼洒,直饮水器的余水量y(升)与接水时间x(分)的函数图象如图,请结合图象回答下列问题:
(1)求当x>5时,y与x之间的函数关系式;
解:设当x>5时,y关于x的函数关系式为y=kx+b,
将(5,9),(7,6)代入y=kx+b中,
解得: ,
∴y=-1.5x+16.5(x>5).
合作探究
当堂检测
学习目标
课堂总结
练一练
(2)假定每人水杯接水0.7升,要使40名学生接水完毕,课间10分钟是否够用?请计算回答.
解:课间10分钟够用.
接水总量为0.7×40=28(升),
理由如下:
饮水机内剩余水量为30-28=2(升),
当时y=2时,有2=-1.5x+16.5,
解得:
∵ <10
∴要使40名学生接水完毕,课间10分钟够用.
合作探究
当堂检测
学习目标
课堂总结
1.小明将父母给的零用钱按每月相等的数额存在储蓄盒内,准备捐给希望工程,盒内钱数y(元)与存钱月数 x(月)之间的关系如图所示,根据下图回答下列问题:
(1)求出y关于x的函数表达式.
解: (1)设函数表达式为y=kx+b,
由图可知图象过(0,40),(4,120)
b=40,
4k+b=120,
∴
40
80
120
y/元
x/月
1
2
3
4
5
o
k=20,
b=40,
解得
∴这个函数的表达式为y=20x+40(x>0).
合作探究
当堂检测
学习目标
课堂总结
1.小明将父母给的零用钱按每月相等的数额存在储蓄盒内,准备捐给希望工程,盒内钱数y(元)与存钱月数 x(月)之间的关系如图所示,根据下图回答下列问题:
(2)根据关系式计算,小明经过几个月才能存够200元?
解:(2)当y=200时,20x+40=200,
∴小明经过8个月才能存够200元.
40
80
120
y/元
x/月
1
2
3
4
5
o
合作探究
当堂检测
学习目标
课堂总结
解得x=8,
2.为节约用水,某市制定以下用水收费标准,每户每月用水不超过8立方米,每立方米收取1元外加0.3元的污水处理费;超过时,超过部分每立方米收取1.5元外加1.2元污水处理费,现设一户每月用水x立方米,应缴水费y元.
(1)求出y关于x的函数解析式;
解:当0≤x≤8时,
y=(1+0.3)x
=1.3x,
当x>8时,
y=(1.5+1.2)(x-8)+1.3×8
=2.7x-11.2
∴y关于x的函数解析式为:
1.3x, (0≤x≤8)
2.7x-11.2. (x>8)
y=
合作探究
当堂检测
学习目标
课堂总结
2.为节约用水,某市制定以下用水收费标准,每户每月用水不超过8立方米,每立方米收取1元外加0.3元的污水处理费;超过时,超过部分每立方米收取1.5元外加1.2元污水处理费,现设一户每月用水x立方米,应缴水费y元.
(2)该市一户某月若用水10立方米时,求应缴水费.
解:当x=10时,
∵10>8,
∴y=2.7×10-11.2
答:应缴水费15.8元.
=15.8(元).
合作探究
当堂检测
学习目标
课堂总结
一次函数的应用
单个一次函数的应用
分段函数图象的应用
合作探究
当堂检测
学习目标
课堂总结
第二十一章 一次函数
21.4 一次函数的应用
第1课时
1.会根据问题情境的数量关系建立相应的一次函数表达式.
2. 掌握单个一次函数的应用.
合作探究
当堂检测
学习目标
课堂总结
探究 利用一次函数解决简单的实际问题
问题提出1:某公司与销售人员签订了这样的工资合同:工资由两部分组成,一部分是基本工资,每人每月3000元;另一部分是按月销售量确定的奖励工资,每销售1件产品,奖励工资10元.要使月工资超过4500元,该月的销售量应当超过多少件?
问题探究:
a.设某销售员销售产品x件,他应得的工资记为y元.列y与x之间的函数关系式.
y=10x+3000
合作探究
当堂检测
学习目标
课堂总结
问题探究:
b.工资超过4500元,该月的销售量应当超过多少件?
10x+3000>4500
解得x>150
要使月工资超过4500元,该月的销售量应当超过150件.
问题解决:
合作探究
当堂检测
学习目标
课堂总结
练一练
1.客运公司规定旅客可免费携带一定质量的行李,当行李质量超过规定时,需付的行李费y(元)是行李质量x(kg)的一次函数,这个函数的图象如图所示.
(1)求y关于x的函数表达式;
(2)某旅客携带25kg的行李时,需要支付多少行李费?
解:(1)设y与x的函数表达式为y=kx+b,
由题意可得:
解得: ,
当y=0时,解得x=10,
合作探究
当堂检测
学习目标
课堂总结
∴ ,
∴ (x≥10).
练一练
1.客运公司规定旅客可免费携带一定质量的行李,当行李质量超过规定时,需付的行李费y(元)是行李质量x(kg)的一次函数,这个函数的图象如图所示.
(2)某旅客携带25kg的行李时,需要支付多少行李费?
故这位旅客需要支付3元行李费.
合作探究
当堂检测
学习目标
课堂总结
(2)当x=25时,y= (元)
探究 利用一次函数解决简单的实际问题
问题提出2:今年以来,广东大部分地区的电力紧缺.电力公司为鼓励市民节约用电,采取按月用电量分段收费的办法,若某户居民每月应缴电费y(元)与用电量x(度)的函数图象是一条折线(如图所示),根据图象解下列问题:
(1)分别写出当0≤x≤100和x>100时,y与x的函数解析式;
合作探究
当堂检测
学习目标
课堂总结
问题探究:
a.当0≤x≤100和x>100时,图象分别经过哪几个点?
当0≤x≤100时,图象经过点(0,0)和(100,65);
当x>100时,图象经过点(100,65)和(130,89).
b.根据上面的已知条件,对你解题有什么启发?
因为函数图象是一条折线,所以解析式要分段讨论,
再根据已知的区间经过的两点,利用待定系数法分别求出每个区间的函数解析式.
合作探究
当堂检测
学习目标
课堂总结
问题解决:
解:设y关于x的函数关系式为y=kx+b,
当0≤x≤100时,将(0,0),(100,65)代入y=kx+b中,
解得: ,
∴y=0.65x(0≤x≤100);
当x>100时,将(100,65),(130,89)代入y=kx+b中,
解得: ,
∴y=0.8x-15(x>100),
y与x的函数解析式也可合起来表示为:
y=
0.65x(0≤x≤100)
0.8x-15(x>100)
{
合作探究
当堂检测
学习目标
课堂总结
探究 利用一次函数解决简单的实际问题
问题提出2:(2)若该用户某月用电62度 ,则应缴费多少元
解:∵62<100,
∴62×0.65
=40.3(元)
答:应缴费40.3元.
a.用电62度是函数解析式中哪个未知数的值?
问题探究:
x
b.应代入哪个解析式求出缴应缴费的多少呢?说说你的理由.
因为62小于100,所以应代入函数y=0.65求出y的值.
问题解决:
合作探究
当堂检测
学习目标
课堂总结
在自变量的不同取值范围内表示函数关系的表达式有不同的形式,这样的函数称为分段函数,分段函数在生活中也有很多应用.
总结归纳
合作探究
当堂检测
学习目标
课堂总结
练一练
2.某校为学生装一台直饮水器,课间学生到直饮水器打水.他们先同时打开全部的水笼头放水,后来又关闭了部分水笼头.假设前后两人接水间隔时间忽略不计,且不发生泼洒,直饮水器的余水量y(升)与接水时间x(分)的函数图象如图,请结合图象回答下列问题:
(1)求当x>5时,y与x之间的函数关系式;
解:设当x>5时,y关于x的函数关系式为y=kx+b,
将(5,9),(7,6)代入y=kx+b中,
解得: ,
∴y=-1.5x+16.5(x>5).
合作探究
当堂检测
学习目标
课堂总结
练一练
(2)假定每人水杯接水0.7升,要使40名学生接水完毕,课间10分钟是否够用?请计算回答.
解:课间10分钟够用.
接水总量为0.7×40=28(升),
理由如下:
饮水机内剩余水量为30-28=2(升),
当时y=2时,有2=-1.5x+16.5,
解得:
∵ <10
∴要使40名学生接水完毕,课间10分钟够用.
合作探究
当堂检测
学习目标
课堂总结
1.小明将父母给的零用钱按每月相等的数额存在储蓄盒内,准备捐给希望工程,盒内钱数y(元)与存钱月数 x(月)之间的关系如图所示,根据下图回答下列问题:
(1)求出y关于x的函数表达式.
解: (1)设函数表达式为y=kx+b,
由图可知图象过(0,40),(4,120)
b=40,
4k+b=120,
∴
40
80
120
y/元
x/月
1
2
3
4
5
o
k=20,
b=40,
解得
∴这个函数的表达式为y=20x+40(x>0).
合作探究
当堂检测
学习目标
课堂总结
1.小明将父母给的零用钱按每月相等的数额存在储蓄盒内,准备捐给希望工程,盒内钱数y(元)与存钱月数 x(月)之间的关系如图所示,根据下图回答下列问题:
(2)根据关系式计算,小明经过几个月才能存够200元?
解:(2)当y=200时,20x+40=200,
∴小明经过8个月才能存够200元.
40
80
120
y/元
x/月
1
2
3
4
5
o
合作探究
当堂检测
学习目标
课堂总结
解得x=8,
2.为节约用水,某市制定以下用水收费标准,每户每月用水不超过8立方米,每立方米收取1元外加0.3元的污水处理费;超过时,超过部分每立方米收取1.5元外加1.2元污水处理费,现设一户每月用水x立方米,应缴水费y元.
(1)求出y关于x的函数解析式;
解:当0≤x≤8时,
y=(1+0.3)x
=1.3x,
当x>8时,
y=(1.5+1.2)(x-8)+1.3×8
=2.7x-11.2
∴y关于x的函数解析式为:
1.3x, (0≤x≤8)
2.7x-11.2. (x>8)
y=
合作探究
当堂检测
学习目标
课堂总结
2.为节约用水,某市制定以下用水收费标准,每户每月用水不超过8立方米,每立方米收取1元外加0.3元的污水处理费;超过时,超过部分每立方米收取1.5元外加1.2元污水处理费,现设一户每月用水x立方米,应缴水费y元.
(2)该市一户某月若用水10立方米时,求应缴水费.
解:当x=10时,
∵10>8,
∴y=2.7×10-11.2
答:应缴水费15.8元.
=15.8(元).
合作探究
当堂检测
学习目标
课堂总结
一次函数的应用
单个一次函数的应用
分段函数图象的应用
合作探究
当堂检测
学习目标
课堂总结
同课章节目录
- 第十八章 数据的收集与整理
- 18.1 统计的初步认识
- 18.2 抽样调查
- 18.3 数据的整理与表示
- 18.4 频数分布表与直方图
- 第十九章 平面直角坐标系
- 19.1 确定平面上物体的位置
- 19.2 平面直角坐标系
- 19.3 坐标与图形的位置
- 19.4 坐标与图形的变化
- 第二十章 函数
- 20.1 常量和变量
- 20.2 函数
- 20.3 函数的表示
- 20.4 函数的初步应用
- 第二十一章 一次函数
- 21.1 一次函数
- 21.2 一次函数的图像和性质
- 21.3 用待定系数法确定一次函数表达式
- 21.4 一次函数的应用
- 21.5 一次函数与二元一次方程的关系
- 第二十二章 四边形
- 22.1 平行四边形的性质
- 22.2 平行四边形的判断
- 22.3 三角形的中位线
- 22.4 矩形
- 22.5 菱形
- 22.6 正方形
- 22.7 多边形的内角和与外角和
