第四章 三角形 单元测试卷 (无答案)2023-2024学年北师大版七年级数学下册
文档属性
| 名称 | 第四章 三角形 单元测试卷 (无答案)2023-2024学年北师大版七年级数学下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 203.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-19 07:28:44 | ||
图片预览



文档简介
第四章 三角形 单元测试卷 2023-2024学年北师大版七年级数学下册
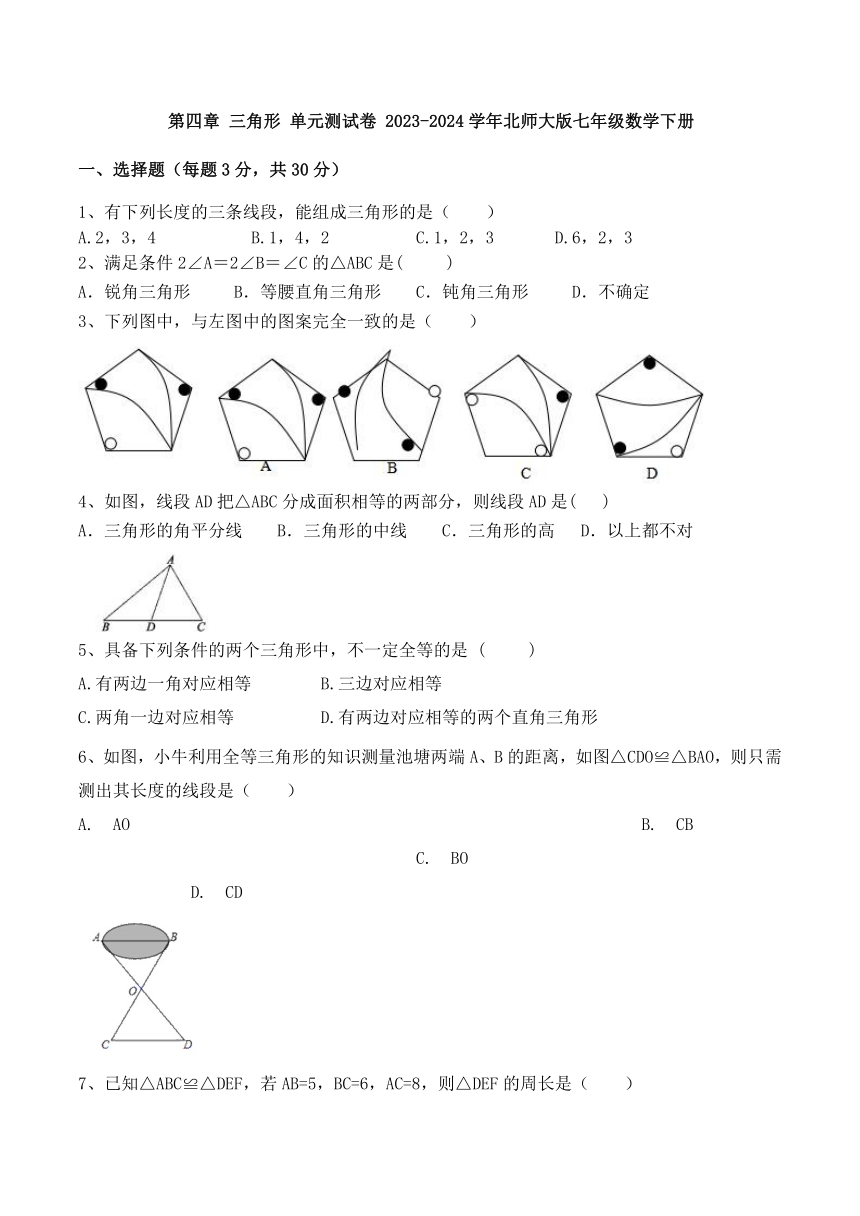
一、选择题(每题3分,共30分)
1、有下列长度的三条线段,能组成三角形的是( )
A.2,3,4 B.1,4,2 C.1,2,3 D.6,2,3
2、满足条件2∠A=2∠B=∠C的△ABC是( )
A.锐角三角形 B.等腰直角三角形 C.钝角三角形 D.不确定
3、下列图中,与左图中的图案完全一致的是( )
4、如图,线段AD把△ABC分成面积相等的两部分,则线段AD是( )
A.三角形的角平分线 B.三角形的中线 C.三角形的高 D.以上都不对
5、具备下列条件的两个三角形中,不一定全等的是 ( )
A.有两边一角对应相等 B.三边对应相等
C.两角一边对应相等 D.有两边对应相等的两个直角三角形
6、如图,小牛利用全等三角形的知识测量池塘两端A、B的距离,如图△CDO≌△BAO,则只需测出其长度的线段是( )
A. AO B. CB C. BO D. CD
7、已知△ABC≌△DEF,若AB=5,BC=6,AC=8,则△DEF的周长是( )
A.8 B.18 C.19 D.20
8、已知:a、b、c是△ABC三边长,且M=(a+b+c)(a+b-c)(a-b-c),那么 ( )
A.M>0 B. M=0 C.M<0 D.不能确定
9、如图,∠A=∠B,∠C=α,DE⊥AC,FD⊥AB,则∠EDF等于( )
A.α B.90°-α C.90°-α D.180°-2α
10、如图所示,在△ABC中,AQ=PQ,PR=PS,∠RAP=∠SAP,PR⊥AB于点R,PS⊥AC于点S,则下列三个结论:①AS=AR;②QP∥AR;③△BPR≌△QPS中( )
A.全部正确 B.仅①和②正确 C.仅①正确 D.仅①和③正确
二、选择题(每小题3分,共18分)
11、如图,为了防止门板变形,小明在门板上钉了一根加固木条,从数学的角度看,这样做的理由是利用了三角形的________.
12、若一个等腰三角形的两边长分别是3 cm和5 cm,则它的周长是 cm.
13、如图,已知△ABC的∠ABC和∠ACB的平分线BE,CF交于点G,若∠BGC=3∠A,则∠A=________°.
14、如图所示,太阳光线AC与A′C′是平行的,AB表示一棵塔松,A′B′表示一棵小杨树,同一时刻两棵树的影长相等,已知塔松高6米,则小杨树高 .
15、如图,△ABC中,∠A=40°,∠B=72°,CE平分∠ACB,CD⊥AB于D,DF⊥CE,则∠CDF=________度.
16、如图,C为线段AE上一动点(不与A、E重合),在AE同侧分别作正三角形ABC和正三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ,以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°.其中完全正确的是 .
三、解答题(共72分)
17、如图,AD⊥BD,AE平分∠BAC,∠B=30°,∠ACD=70°.求∠DAE的度数.
18、如图,点是的边上的一点,点为的中点,过点作交的延长线于点,求证:。
19、如图,已知△ABC,(1)作∠BAC的角平分线交于BC于点D(要求尺规作图,不写作法);
(2)若AB=AC=5,BC=6,求AD的长.
20、如图,在△ABC中,∠ACB=90°,CD是AB边上的高,AB=13cm,BC=12cm,AC=5cm,求:(1)△ABC的面积;(2)CD的长.
21、学校进行跳高比赛,要看横杆AB的两端到地面的高度AC、BD是否相同,小明发现这时AC、DB在地面上的影子的长度CE、FD相同,于是他就断定木杆两端和地面的高度相同,他说的对吗?为什么?
2、如图,两根旗杆相距12m,某人从B点沿BA走向A点,一段时间后他到达点M,此时他仰望旗杆的顶点C和D,两次视线的夹角为90°,且CM=DM,已知旗杆AC的高为3m,该人的运动速度为1m/s,求:这个人从B点到M点运动了多长时间?
23、将一副三角板拼成如图所示的图形,过点作平分交于点。
(1)求证:;
(2)求的度数.
24、已知△ABC中,∠ABC=∠ACB,D为线段CB上一点(不与C,B重合),点E为射线CA上一点,∠ADE=∠AED,设∠BAD=α,∠CDE=β.
(1)如图(1),
①若∠BAC=42°,∠DAE=30°,则α=________,β=________.
②若∠BAC=54°,∠DAE=36°,则α=________,β=________.
③写出α与β的数量关系,并说明理由;
(2)如图(2),当E点在CA的延长线上时,其它条件不变,请直接写出α与β的数量关系.
25、在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)当直线MN绕点C旋转到图甲的位置时,试说明:①△ADC≌△CEB;②DE=AD+BE;
(2)当直线MN绕点C旋转到图乙的位置时,试说明:DE=AD-BE;
(3)当直线MN绕点C旋转到图丙的位置时,试问DE、AD、BE具有怎样的等量关系?请写出这个等量关系,并加以证明.
一、选择题(每题3分,共30分)
1、有下列长度的三条线段,能组成三角形的是( )
A.2,3,4 B.1,4,2 C.1,2,3 D.6,2,3
2、满足条件2∠A=2∠B=∠C的△ABC是( )
A.锐角三角形 B.等腰直角三角形 C.钝角三角形 D.不确定
3、下列图中,与左图中的图案完全一致的是( )
4、如图,线段AD把△ABC分成面积相等的两部分,则线段AD是( )
A.三角形的角平分线 B.三角形的中线 C.三角形的高 D.以上都不对
5、具备下列条件的两个三角形中,不一定全等的是 ( )
A.有两边一角对应相等 B.三边对应相等
C.两角一边对应相等 D.有两边对应相等的两个直角三角形
6、如图,小牛利用全等三角形的知识测量池塘两端A、B的距离,如图△CDO≌△BAO,则只需测出其长度的线段是( )
A. AO B. CB C. BO D. CD
7、已知△ABC≌△DEF,若AB=5,BC=6,AC=8,则△DEF的周长是( )
A.8 B.18 C.19 D.20
8、已知:a、b、c是△ABC三边长,且M=(a+b+c)(a+b-c)(a-b-c),那么 ( )
A.M>0 B. M=0 C.M<0 D.不能确定
9、如图,∠A=∠B,∠C=α,DE⊥AC,FD⊥AB,则∠EDF等于( )
A.α B.90°-α C.90°-α D.180°-2α
10、如图所示,在△ABC中,AQ=PQ,PR=PS,∠RAP=∠SAP,PR⊥AB于点R,PS⊥AC于点S,则下列三个结论:①AS=AR;②QP∥AR;③△BPR≌△QPS中( )
A.全部正确 B.仅①和②正确 C.仅①正确 D.仅①和③正确
二、选择题(每小题3分,共18分)
11、如图,为了防止门板变形,小明在门板上钉了一根加固木条,从数学的角度看,这样做的理由是利用了三角形的________.
12、若一个等腰三角形的两边长分别是3 cm和5 cm,则它的周长是 cm.
13、如图,已知△ABC的∠ABC和∠ACB的平分线BE,CF交于点G,若∠BGC=3∠A,则∠A=________°.
14、如图所示,太阳光线AC与A′C′是平行的,AB表示一棵塔松,A′B′表示一棵小杨树,同一时刻两棵树的影长相等,已知塔松高6米,则小杨树高 .
15、如图,△ABC中,∠A=40°,∠B=72°,CE平分∠ACB,CD⊥AB于D,DF⊥CE,则∠CDF=________度.
16、如图,C为线段AE上一动点(不与A、E重合),在AE同侧分别作正三角形ABC和正三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ,以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°.其中完全正确的是 .
三、解答题(共72分)
17、如图,AD⊥BD,AE平分∠BAC,∠B=30°,∠ACD=70°.求∠DAE的度数.
18、如图,点是的边上的一点,点为的中点,过点作交的延长线于点,求证:。
19、如图,已知△ABC,(1)作∠BAC的角平分线交于BC于点D(要求尺规作图,不写作法);
(2)若AB=AC=5,BC=6,求AD的长.
20、如图,在△ABC中,∠ACB=90°,CD是AB边上的高,AB=13cm,BC=12cm,AC=5cm,求:(1)△ABC的面积;(2)CD的长.
21、学校进行跳高比赛,要看横杆AB的两端到地面的高度AC、BD是否相同,小明发现这时AC、DB在地面上的影子的长度CE、FD相同,于是他就断定木杆两端和地面的高度相同,他说的对吗?为什么?
2、如图,两根旗杆相距12m,某人从B点沿BA走向A点,一段时间后他到达点M,此时他仰望旗杆的顶点C和D,两次视线的夹角为90°,且CM=DM,已知旗杆AC的高为3m,该人的运动速度为1m/s,求:这个人从B点到M点运动了多长时间?
23、将一副三角板拼成如图所示的图形,过点作平分交于点。
(1)求证:;
(2)求的度数.
24、已知△ABC中,∠ABC=∠ACB,D为线段CB上一点(不与C,B重合),点E为射线CA上一点,∠ADE=∠AED,设∠BAD=α,∠CDE=β.
(1)如图(1),
①若∠BAC=42°,∠DAE=30°,则α=________,β=________.
②若∠BAC=54°,∠DAE=36°,则α=________,β=________.
③写出α与β的数量关系,并说明理由;
(2)如图(2),当E点在CA的延长线上时,其它条件不变,请直接写出α与β的数量关系.
25、在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)当直线MN绕点C旋转到图甲的位置时,试说明:①△ADC≌△CEB;②DE=AD+BE;
(2)当直线MN绕点C旋转到图乙的位置时,试说明:DE=AD-BE;
(3)当直线MN绕点C旋转到图丙的位置时,试问DE、AD、BE具有怎样的等量关系?请写出这个等量关系,并加以证明.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
