2024年中考 数学专题提升12 反比例函数的图象与性质(含答案)
文档属性
| 名称 | 2024年中考 数学专题提升12 反比例函数的图象与性质(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 397.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-19 07:32:28 | ||
图片预览




文档简介
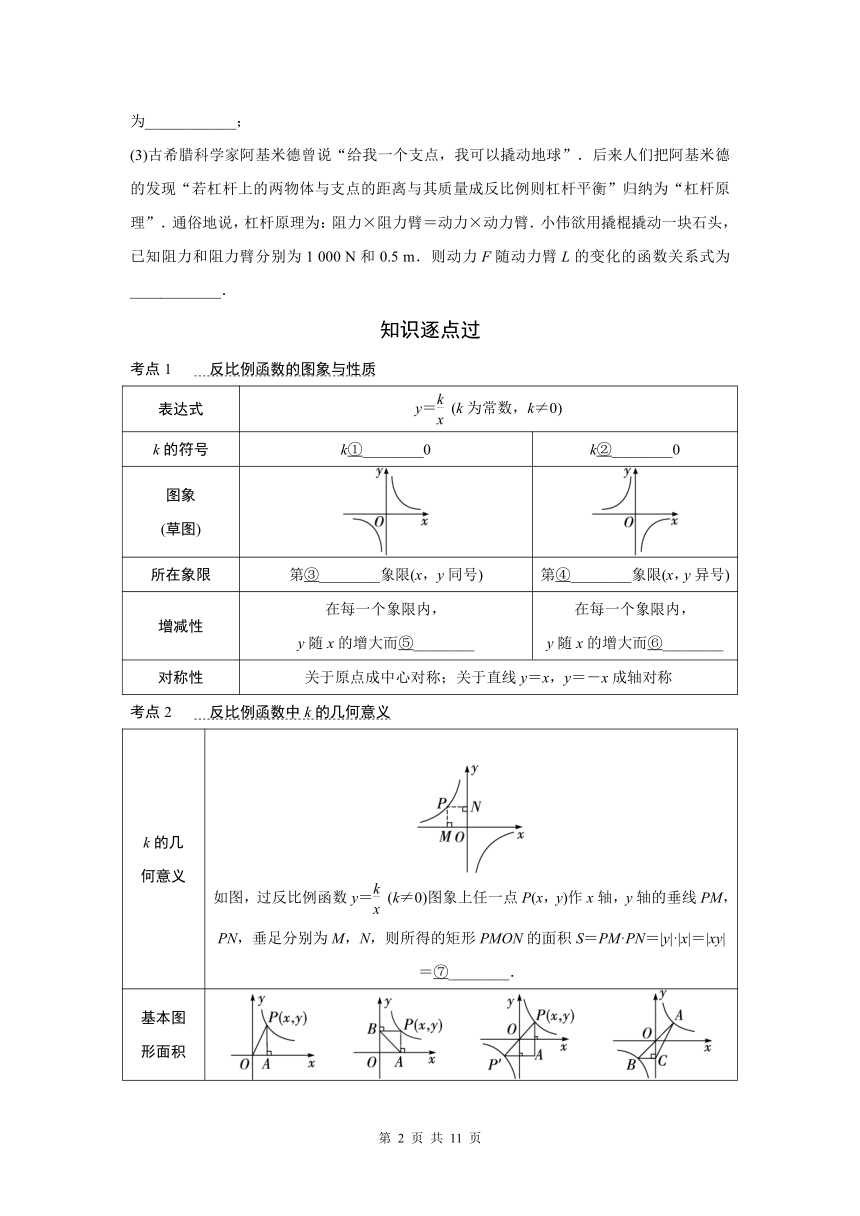
反比例函数的图象与性质
1. 已知反比例函数y=(k≠0).
(1)当反比例函数图象在第二、四象限时,k的取值范围为________,在每一个象限内,y随x的增大而________;(填“增大”或“减小”)
(2)若点A(3,-4),B(-2,m)在该反比例函数图象上,则m的值为________;
(3)若k>0,在这个反比例函数的图象上有两点A(1,y1),B(4,y2),则y1,y2的大小关系为________________________________________________________________________;
(4)若点A(x,y1),B(-x,y2)在该反比例函数图象上,则y1+y2=________;
(5)在同一直角坐标系中,函数y=(k≠0)和y=kx+1(k≠0)的图象大致为________.
第1题图
2. 如图,A,B是反比例函数y=图象上的两点,过点A,B作y轴的垂线,垂足分别为E,F,作x轴的垂线,垂足分别为G,H,连接OA.
第2题图
(1)△OAG的面积为________;
(2)矩形OEAG的面积为________,矩形OFBH的面积为________;
(3)若S矩形OFMG=3,S矩形FEAM+S矩形HBMG的值为________.
3. 根据下列实际问题,列函数关系式:
(1)某村有耕地200 km2,人口数量x逐年发生变化,该村人均耕地面积y km2与x之间的函数关系式为________;
(2)某市距省城248 km,汽车行驶全程所需的时间t h与平均速度v km/h之间的函数关系式为____________;
(3)古希腊科学家阿基米德曾说“给我一个支点,我可以撬动地球”.后来人们把阿基米德的发现“若杠杆上的两物体与支点的距离与其质量成反比例则杠杆平衡”归纳为“杠杆原理”.通俗地说,杠杆原理为:阻力×阻力臂=动力×动力臂.小伟欲用撬棍撬动一块石头,已知阻力和阻力臂分别为1 000 N和0.5 m.则动力F随动力臂L的变化的函数关系式为____________.
知识逐点过
考点1 反比例函数的图象与性质
表达式 y=(k为常数,k≠0)
k的符号 k①________0 k②________0
图象(草图)
所在象限 第③________象限(x,y同号) 第④________象限(x,y异号)
增减性 在每一个象限内,y随x的增大而⑤________ 在每一个象限内,y随x的增大而⑥________
对称性 关于原点成中心对称;关于直线y=x,y=-x成轴对称
考点2 反比例函数中k的几何意义
k的几何意义 如图,过反比例函数y=(k≠0)图象上任一点P(x,y)作x轴,y轴的垂线PM,PN,垂足分别为M,N,则所得的矩形PMON的面积S=PM·PN=|y|·|x|=|xy|=⑦________.
基本图形面积 S△AOP=⑧____ S△ABP=⑨____ S△APP′=2|k| S△ABC=⑩____ S ABCD= ____
考点3 反比例函数解析式的确定
待定系数法 1.设所求反比例函数解析式为y=(k≠0);2.找出图象上的一点P(a,b);3.将点P的坐标代入y=中,得k= ________;4.确定反比例函数解析式y=
利用k的几何意义 若题中已知面积时,考虑用k的几何意义求解,由面积得|k|,再结合图象所在象限判断k的正负,从而得出k的值,代入解析式即可
考点4 反比例函数的实际应用
特征 反比例函数应用主要是通过实例构建反比例函数模型,即通过题意或图象,列出关系式,根据图象和性质解决问题
解题方法 1.分析实际问题中变量之间的关系;2.建立反比例函数模型;3.用反比例函数的有关知识解答,注意利用反比例函数两变量之积是定值的性质,算出定值
常见应用 路程(s)一定,速度(v)和时间(t)成反比例,即v=;矩形面积(S)一定,长(y)和宽(x)成反比例,即y=;电压(U)一定,电流(I)和电阻(R)成反比例,即I=;容积(V)一定,排水速度(Q)和排水时间(t)成反比例,即Q=
【温馨提示】在反比例函数实际应用题中,要注意自变量的取值范围,有时候只是反比例函数图象的一支或一段
真题演练
命题点1 反比例函数的图象与性质
1. 如图,在同一平面直角坐标系中,直线y=k1x(k1≠0)与双曲线y=(k2≠0)相交于A,B两点,已知点A的坐标为(1,2),则点B的坐标为( )
A. (-1,-2) B. (-2,-1) C. (-1,-1) D. (-2,-2)
第1题图
2. 点(1,y1),(2,y2),(3,y3),(4,y4)在反比例函数y=图象上,则y1,y2,y3,y4中最小的是( )
A. y1 B. y2 C. y3 D. y4
命题点2 反比例函数的实际应用
3. 某蓄电池的电压为48 V,使用此蓄电池时,电流I(单位:A)与电阻R(单位:Ω)的函数表达式为I=.当R=12 Ω时,I的值为________A.
拓展训练
4. 在温度不变的条件下,通过一次又一次地对汽缸顶部的活塞加压,加压后气体对汽缸壁所产生的压强p(kPa)与汽缸内气体的体积V(mL)成反比例,p关于 V的函数图象如图所示.若压强由 75 kPa加压到100 kPa,则气体体积压缩了________ mL.
第4题图
基础过关
1. 若点A(1,3)是反比例函数y=(k≠0)图象上一点,则常数k的值为( )
A. 3 B. -3 C. D. -
2. 反比例函数y=-的图象一定经过的点是( )
A. (1,4) B. (-1,-4) C. (-2,2) D. (2,2)
3. 关于反比例函数y=,下列结论正确的是( )
A. 图象位于第二、四象限
B. 图象与坐标轴有公共点
C. 图象所在的每一个象限内,y随x的增大而减小
D. 图象经过点(a,a+2),则a=1
4. 已知点M(2,a)在反比例函数y=的图象上,其中a,k为常数,且k>0,则点M定在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
5.如图,一次函数y1=k1x+b(k1>0)的图象与反比例函数y2=(k2>0)的图象相交于点A的横坐标为1,点B的横坐标为-2,当y1第5题图
A. x<-2或x>1
B. x<-2或0C. -21
D. -26. 若点A(-3,a),B(-1,b),C(2,c)都在反比例函数y=(k<0)的图象上,则
a,b,c的大小关系用“<”连接的结果为( )
A. b7. 一次函数y=ax+b与反比例函数y=(a,b为常数且均不等于0)在同一坐标系内的图象可能是( )
ABCD
8. 如图,在平面直角坐标系中,点A在反比例函数y=(k为常数,k>0,x>0)的图象上,过点A作x轴的垂线,垂足为点B,连接OA.若△OAB的面积为,则k=__________.
第8题图
9.已知点A(-2,3)在反比例函数y=(k≠0)的图象上,点B(a,3)在反比例函数y=(k≠0)的图象上,则a的值为__________.
10. 某农场有一个储水量为8 m3的圆柱形储水罐,现计划对农场进行改造,需减少储水罐的占地面积.在储水量不变的前提下,储水罐的高度h(m)与底面积S(m2)成反比例函数关系,则当储水罐底面积由5 m2变为4 m2时,高增加了__________m.
11.科学课上,同学用自制密度计测量液体的密度.密度计悬浮在不同的液体中时,浸在液体中的高度h(单位:cm)是液体的密度ρ(单位:g/cm3)的反比例函数,当密度计悬浮在密度为1 g/cm3的水中时,h=20 cm.
(1)求h关于ρ的函数解析式;
(2)当密度计悬浮在另一种液体中时,h=25 cm,求该液体的密度ρ.
第11题图
12. 已知反比例函数y=(k≠0)的图象的一支如图所示,它经过点(3,-2).
(1)求这个反比例函数的表达式,并补画该函数图象的另一支;
(2)求当y≤5,且y≠0时自变量x的取值范围.
第12题图
综合提升
13. 已知点A(3,3),B(3,1),反比例函数y=(k≠0)图象的一支与线段AB有交点,写出一个符合条件的k的整数值:__________.
第13题图
反比例函数的图象与性质(答案)
1. (1)k<0,增大
(2)6 【解析】将点A(3,-4)代入y=,解得k=-12,将点B(-2,m)代入y=-,解得m=6.
(3)y1>y2 【解析】当反比例函数图象在第一、三象限时,k>0,∴在每一个象限内,y随x的增大而减小,∵1<4,∴y1>y2.
(4)0 【解析】∵点A(x,y1),B(-x,y2)在反比例函数图象上,∴xy1=-xy2,∴y1=-y2,∴y1+y2=0.
(5)③ 【解析】∵一次函数解析式为y=kx+1,∴当k>0时,一次函数图象经过第一、二、三象限,反比例函数图象经过第一、三象限;当k<0时,一次函数图象经过第一、二、四象限,反比例函数图象经过第二、四象限,∴③满足.
2. (1) 【解析】∵反比例函数解析式为y=,点A在反比例函数的图象上,∴S△OAG==.
(2)9,9 【解析】S矩形OEAG=|k|=9,S矩形OFBH=|k|=9.
(3)12 【解析】∵S矩形OGAE=S矩形OFBH=9,S矩形OFMG=3,∴S矩形HBMG=S矩形FEAM=9-3=6,∴S矩形HBMG+S矩形FEAM=12.
(1)y=(x为正整数);(2)t=(v>0);(3)F=(L>0)
知识逐点过
①> ②< ③一、三 ④二、四 ⑤减小 ⑥增大 ⑦|k| ⑧|k|
⑨|k| ⑩|k| |k| ab
真题演练
1. A 【解析】∵点A与点B关于原点对称,∴点B的坐标为(-1,-2).
2. D 【解析】∵点(1,y1),(2,y2),(3,y3),(4,y4)在反比例函数y=的图象上,且反比例函数y=的图象在第一象限内y随x的增大而减小,∴y1>y2>y3>y4,∴最小的是y4.
3. 4 【解析】当R=12 Ω时,I==4(A).
4. 20 【解析】设函数表达式是p=,代入点(100,60)得出函数表达式是p=,当p=75 kPa时,V=80 mL;当p=100 kPa时,V=60 mL.因此气体体积压缩了80-60=20(mL).
基础过关
1. A 【解析】 把A(1,3)代入y=中,得3=,解得k=3.
2. C
3. C 【解析】A.k=3>0,则反比例函数图象两个分支分布在第一、三象限,故不符合题意;B.反比例函数图象与坐标轴没有公共点,故不符合题意;C.当x>0时,y随x的增大而减小;当x<0时,y随x的增大而减小,故符合题意;D.图象经过点(a,a+2),∴a(a+2)=3,解得a1=1,a2=-3,故不符合题意.
4. A 【解析】∵k>0,∴反比例函数y=的图象经过第一、三象限,故点M可能在第一象限或第三象限,∵M(2,a)的横坐标大于0,∴M(2,a)一定在第一象限.
5. B 【解析】∵一次函数与反比例函数图象的交点横坐标分别是-2与1,∴由题图可知,当x<-2时,y1<y2;当0<x<1时,y1<y2,∴x的取值范围是x<-2或06. D 【解析】∵反比例函数的表达式为y=(k<0),∴函数的图象位于第二、四象限,∴在第二、四象限内,y随x的增大而增大.∵A(-3,a),B(-1,b),-3<-1<0,A,B两点都在第二象限,∴a<b,又∵C(2,c),2>0,C点在第四象限,∴c<0,∴c<a<b.
7. D 【解析】 A.一次函数y=ax+b的图象经过第一、二、三象限,则a>0,b>0,所以ab>0,则反比例函数y=的图象应该位于第一、三象限,故A选项不可能;B.一次函数y=ax+b的图象经过第一、二、四象限,则a<0,b>0,所以ab<0,则反比例函数y=的图象应该位于第二、四象限,故B选项不可能;C.一次函数y=ax+b的图象经过第一、三、四象限,则a>0,b<0,所以ab<0,则反比例函数y=的图象应该位于第二、四象限,故C选项不可能;D.一次函数y=ax+b的图象经过第一、二、四象限,则a<0,b>0,所以ab<0,则反比例函数y=的图象应该位于第二、四象限,故D选项有可能.
8. 【解析】设点A(x,y),∵点A在反比例函数y=的图象上,∴k=xy.∵点A在第一象限,且AB⊥x轴于点B,∴OB=x,AB=y.∵S△OAB=,∴xy=,∴xy=,∴k=xy=.
9. 2 【解析】 ∵点A(-2,3)在反比例函数y=(k≠0)的图象上,∴k=(-2)×3=-6,∴反比例函数y==.将点B(a, 3)代入y=中,得3=,解得a=2.
【一题多解】 ∵反比例函数y=(k≠0)的图象与反比例函数y=(k≠0)的图象关于y轴对称,且点A的纵坐标与点B的纵坐标相等,∴点A的横坐标与点B的横坐标关于y轴对称,∴a=-(-2)=2.
10. 【解析】根据圆柱体积=底面积×高可知,h=,当S=5时,h=,当S=4时,h=2,2-=,∴当储水罐底面积由5 m2变为4 m2时,高增加了 m.
11. 解:(1)设h关于ρ的函数解析式为h=(ρ>0),
把ρ=1,h=20代入解析式,得k=1×20=20,
∴h关于ρ的函数解析式为h=(ρ>0);
(2)把h=25代入h=,
得25=,解得ρ=0.8.
答:该液体的密度ρ为0.8 g/cm3.
12. 解:(1)把点(3,-2)代入反比例函数y=(k≠0),
得-2=,∴k=-6,
∴反比例函数的表达式是y=-.
反比例函数图象的另一支如解图;
第12题解图
(2)当y=5时,5=-,解得x=-.
由图象可知,当y≤5,且y≠0时,
自变量x的取值范围是x≤-或x>0.
13. 4(答案不唯一,符合3≤k≤9即可) 【解析】当y=(k≠0)的图象经过点A(3,3)时,则3=,解得k=9;当y=(k≠0)的图象经过点B(3,1)时,则1=,解得k=3,∴反比例函数图象的一支与线段AB有交点时,k的取值范围为3≤k≤9,∴符合条件的k的整数值可以为3,4,5,6,7,8,9.
1. 已知反比例函数y=(k≠0).
(1)当反比例函数图象在第二、四象限时,k的取值范围为________,在每一个象限内,y随x的增大而________;(填“增大”或“减小”)
(2)若点A(3,-4),B(-2,m)在该反比例函数图象上,则m的值为________;
(3)若k>0,在这个反比例函数的图象上有两点A(1,y1),B(4,y2),则y1,y2的大小关系为________________________________________________________________________;
(4)若点A(x,y1),B(-x,y2)在该反比例函数图象上,则y1+y2=________;
(5)在同一直角坐标系中,函数y=(k≠0)和y=kx+1(k≠0)的图象大致为________.
第1题图
2. 如图,A,B是反比例函数y=图象上的两点,过点A,B作y轴的垂线,垂足分别为E,F,作x轴的垂线,垂足分别为G,H,连接OA.
第2题图
(1)△OAG的面积为________;
(2)矩形OEAG的面积为________,矩形OFBH的面积为________;
(3)若S矩形OFMG=3,S矩形FEAM+S矩形HBMG的值为________.
3. 根据下列实际问题,列函数关系式:
(1)某村有耕地200 km2,人口数量x逐年发生变化,该村人均耕地面积y km2与x之间的函数关系式为________;
(2)某市距省城248 km,汽车行驶全程所需的时间t h与平均速度v km/h之间的函数关系式为____________;
(3)古希腊科学家阿基米德曾说“给我一个支点,我可以撬动地球”.后来人们把阿基米德的发现“若杠杆上的两物体与支点的距离与其质量成反比例则杠杆平衡”归纳为“杠杆原理”.通俗地说,杠杆原理为:阻力×阻力臂=动力×动力臂.小伟欲用撬棍撬动一块石头,已知阻力和阻力臂分别为1 000 N和0.5 m.则动力F随动力臂L的变化的函数关系式为____________.
知识逐点过
考点1 反比例函数的图象与性质
表达式 y=(k为常数,k≠0)
k的符号 k①________0 k②________0
图象(草图)
所在象限 第③________象限(x,y同号) 第④________象限(x,y异号)
增减性 在每一个象限内,y随x的增大而⑤________ 在每一个象限内,y随x的增大而⑥________
对称性 关于原点成中心对称;关于直线y=x,y=-x成轴对称
考点2 反比例函数中k的几何意义
k的几何意义 如图,过反比例函数y=(k≠0)图象上任一点P(x,y)作x轴,y轴的垂线PM,PN,垂足分别为M,N,则所得的矩形PMON的面积S=PM·PN=|y|·|x|=|xy|=⑦________.
基本图形面积 S△AOP=⑧____ S△ABP=⑨____ S△APP′=2|k| S△ABC=⑩____ S ABCD= ____
考点3 反比例函数解析式的确定
待定系数法 1.设所求反比例函数解析式为y=(k≠0);2.找出图象上的一点P(a,b);3.将点P的坐标代入y=中,得k= ________;4.确定反比例函数解析式y=
利用k的几何意义 若题中已知面积时,考虑用k的几何意义求解,由面积得|k|,再结合图象所在象限判断k的正负,从而得出k的值,代入解析式即可
考点4 反比例函数的实际应用
特征 反比例函数应用主要是通过实例构建反比例函数模型,即通过题意或图象,列出关系式,根据图象和性质解决问题
解题方法 1.分析实际问题中变量之间的关系;2.建立反比例函数模型;3.用反比例函数的有关知识解答,注意利用反比例函数两变量之积是定值的性质,算出定值
常见应用 路程(s)一定,速度(v)和时间(t)成反比例,即v=;矩形面积(S)一定,长(y)和宽(x)成反比例,即y=;电压(U)一定,电流(I)和电阻(R)成反比例,即I=;容积(V)一定,排水速度(Q)和排水时间(t)成反比例,即Q=
【温馨提示】在反比例函数实际应用题中,要注意自变量的取值范围,有时候只是反比例函数图象的一支或一段
真题演练
命题点1 反比例函数的图象与性质
1. 如图,在同一平面直角坐标系中,直线y=k1x(k1≠0)与双曲线y=(k2≠0)相交于A,B两点,已知点A的坐标为(1,2),则点B的坐标为( )
A. (-1,-2) B. (-2,-1) C. (-1,-1) D. (-2,-2)
第1题图
2. 点(1,y1),(2,y2),(3,y3),(4,y4)在反比例函数y=图象上,则y1,y2,y3,y4中最小的是( )
A. y1 B. y2 C. y3 D. y4
命题点2 反比例函数的实际应用
3. 某蓄电池的电压为48 V,使用此蓄电池时,电流I(单位:A)与电阻R(单位:Ω)的函数表达式为I=.当R=12 Ω时,I的值为________A.
拓展训练
4. 在温度不变的条件下,通过一次又一次地对汽缸顶部的活塞加压,加压后气体对汽缸壁所产生的压强p(kPa)与汽缸内气体的体积V(mL)成反比例,p关于 V的函数图象如图所示.若压强由 75 kPa加压到100 kPa,则气体体积压缩了________ mL.
第4题图
基础过关
1. 若点A(1,3)是反比例函数y=(k≠0)图象上一点,则常数k的值为( )
A. 3 B. -3 C. D. -
2. 反比例函数y=-的图象一定经过的点是( )
A. (1,4) B. (-1,-4) C. (-2,2) D. (2,2)
3. 关于反比例函数y=,下列结论正确的是( )
A. 图象位于第二、四象限
B. 图象与坐标轴有公共点
C. 图象所在的每一个象限内,y随x的增大而减小
D. 图象经过点(a,a+2),则a=1
4. 已知点M(2,a)在反比例函数y=的图象上,其中a,k为常数,且k>0,则点M定在( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
5.如图,一次函数y1=k1x+b(k1>0)的图象与反比例函数y2=(k2>0)的图象相交于点A的横坐标为1,点B的横坐标为-2,当y1
A. x<-2或x>1
B. x<-2或0
D. -2
a,b,c的大小关系用“<”连接的结果为( )
A. b
ABCD
8. 如图,在平面直角坐标系中,点A在反比例函数y=(k为常数,k>0,x>0)的图象上,过点A作x轴的垂线,垂足为点B,连接OA.若△OAB的面积为,则k=__________.
第8题图
9.已知点A(-2,3)在反比例函数y=(k≠0)的图象上,点B(a,3)在反比例函数y=(k≠0)的图象上,则a的值为__________.
10. 某农场有一个储水量为8 m3的圆柱形储水罐,现计划对农场进行改造,需减少储水罐的占地面积.在储水量不变的前提下,储水罐的高度h(m)与底面积S(m2)成反比例函数关系,则当储水罐底面积由5 m2变为4 m2时,高增加了__________m.
11.科学课上,同学用自制密度计测量液体的密度.密度计悬浮在不同的液体中时,浸在液体中的高度h(单位:cm)是液体的密度ρ(单位:g/cm3)的反比例函数,当密度计悬浮在密度为1 g/cm3的水中时,h=20 cm.
(1)求h关于ρ的函数解析式;
(2)当密度计悬浮在另一种液体中时,h=25 cm,求该液体的密度ρ.
第11题图
12. 已知反比例函数y=(k≠0)的图象的一支如图所示,它经过点(3,-2).
(1)求这个反比例函数的表达式,并补画该函数图象的另一支;
(2)求当y≤5,且y≠0时自变量x的取值范围.
第12题图
综合提升
13. 已知点A(3,3),B(3,1),反比例函数y=(k≠0)图象的一支与线段AB有交点,写出一个符合条件的k的整数值:__________.
第13题图
反比例函数的图象与性质(答案)
1. (1)k<0,增大
(2)6 【解析】将点A(3,-4)代入y=,解得k=-12,将点B(-2,m)代入y=-,解得m=6.
(3)y1>y2 【解析】当反比例函数图象在第一、三象限时,k>0,∴在每一个象限内,y随x的增大而减小,∵1<4,∴y1>y2.
(4)0 【解析】∵点A(x,y1),B(-x,y2)在反比例函数图象上,∴xy1=-xy2,∴y1=-y2,∴y1+y2=0.
(5)③ 【解析】∵一次函数解析式为y=kx+1,∴当k>0时,一次函数图象经过第一、二、三象限,反比例函数图象经过第一、三象限;当k<0时,一次函数图象经过第一、二、四象限,反比例函数图象经过第二、四象限,∴③满足.
2. (1) 【解析】∵反比例函数解析式为y=,点A在反比例函数的图象上,∴S△OAG==.
(2)9,9 【解析】S矩形OEAG=|k|=9,S矩形OFBH=|k|=9.
(3)12 【解析】∵S矩形OGAE=S矩形OFBH=9,S矩形OFMG=3,∴S矩形HBMG=S矩形FEAM=9-3=6,∴S矩形HBMG+S矩形FEAM=12.
(1)y=(x为正整数);(2)t=(v>0);(3)F=(L>0)
知识逐点过
①> ②< ③一、三 ④二、四 ⑤减小 ⑥增大 ⑦|k| ⑧|k|
⑨|k| ⑩|k| |k| ab
真题演练
1. A 【解析】∵点A与点B关于原点对称,∴点B的坐标为(-1,-2).
2. D 【解析】∵点(1,y1),(2,y2),(3,y3),(4,y4)在反比例函数y=的图象上,且反比例函数y=的图象在第一象限内y随x的增大而减小,∴y1>y2>y3>y4,∴最小的是y4.
3. 4 【解析】当R=12 Ω时,I==4(A).
4. 20 【解析】设函数表达式是p=,代入点(100,60)得出函数表达式是p=,当p=75 kPa时,V=80 mL;当p=100 kPa时,V=60 mL.因此气体体积压缩了80-60=20(mL).
基础过关
1. A 【解析】 把A(1,3)代入y=中,得3=,解得k=3.
2. C
3. C 【解析】A.k=3>0,则反比例函数图象两个分支分布在第一、三象限,故不符合题意;B.反比例函数图象与坐标轴没有公共点,故不符合题意;C.当x>0时,y随x的增大而减小;当x<0时,y随x的增大而减小,故符合题意;D.图象经过点(a,a+2),∴a(a+2)=3,解得a1=1,a2=-3,故不符合题意.
4. A 【解析】∵k>0,∴反比例函数y=的图象经过第一、三象限,故点M可能在第一象限或第三象限,∵M(2,a)的横坐标大于0,∴M(2,a)一定在第一象限.
5. B 【解析】∵一次函数与反比例函数图象的交点横坐标分别是-2与1,∴由题图可知,当x<-2时,y1<y2;当0<x<1时,y1<y2,∴x的取值范围是x<-2或0
7. D 【解析】 A.一次函数y=ax+b的图象经过第一、二、三象限,则a>0,b>0,所以ab>0,则反比例函数y=的图象应该位于第一、三象限,故A选项不可能;B.一次函数y=ax+b的图象经过第一、二、四象限,则a<0,b>0,所以ab<0,则反比例函数y=的图象应该位于第二、四象限,故B选项不可能;C.一次函数y=ax+b的图象经过第一、三、四象限,则a>0,b<0,所以ab<0,则反比例函数y=的图象应该位于第二、四象限,故C选项不可能;D.一次函数y=ax+b的图象经过第一、二、四象限,则a<0,b>0,所以ab<0,则反比例函数y=的图象应该位于第二、四象限,故D选项有可能.
8. 【解析】设点A(x,y),∵点A在反比例函数y=的图象上,∴k=xy.∵点A在第一象限,且AB⊥x轴于点B,∴OB=x,AB=y.∵S△OAB=,∴xy=,∴xy=,∴k=xy=.
9. 2 【解析】 ∵点A(-2,3)在反比例函数y=(k≠0)的图象上,∴k=(-2)×3=-6,∴反比例函数y==.将点B(a, 3)代入y=中,得3=,解得a=2.
【一题多解】 ∵反比例函数y=(k≠0)的图象与反比例函数y=(k≠0)的图象关于y轴对称,且点A的纵坐标与点B的纵坐标相等,∴点A的横坐标与点B的横坐标关于y轴对称,∴a=-(-2)=2.
10. 【解析】根据圆柱体积=底面积×高可知,h=,当S=5时,h=,当S=4时,h=2,2-=,∴当储水罐底面积由5 m2变为4 m2时,高增加了 m.
11. 解:(1)设h关于ρ的函数解析式为h=(ρ>0),
把ρ=1,h=20代入解析式,得k=1×20=20,
∴h关于ρ的函数解析式为h=(ρ>0);
(2)把h=25代入h=,
得25=,解得ρ=0.8.
答:该液体的密度ρ为0.8 g/cm3.
12. 解:(1)把点(3,-2)代入反比例函数y=(k≠0),
得-2=,∴k=-6,
∴反比例函数的表达式是y=-.
反比例函数图象的另一支如解图;
第12题解图
(2)当y=5时,5=-,解得x=-.
由图象可知,当y≤5,且y≠0时,
自变量x的取值范围是x≤-或x>0.
13. 4(答案不唯一,符合3≤k≤9即可) 【解析】当y=(k≠0)的图象经过点A(3,3)时,则3=,解得k=9;当y=(k≠0)的图象经过点B(3,1)时,则1=,解得k=3,∴反比例函数图象的一支与线段AB有交点时,k的取值范围为3≤k≤9,∴符合条件的k的整数值可以为3,4,5,6,7,8,9.
同课章节目录
