新课标A版选修1-13.4生活中的优化问题举例
文档属性
| 名称 | 新课标A版选修1-13.4生活中的优化问题举例 |

|
|
| 格式 | rar | ||
| 文件大小 | 245.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-03-23 00:00:00 | ||
图片预览






文档简介
课件18张PPT。3.4 生活中的优化问题举例新课引入: 导数在实际生活中有着广泛的应用,利用导数求最值的方法,可以求出实际生活中的某些最值问题.1.几何方面的应用2.物理方面的应用.3.经济学方面的应用(面积和体积等的最值)(利润方面最值)(功和功率等最值)例1.海报版面尺寸的设计
学校或班级举行活动,通常需要张贴海报进行宣传。现让你设计一张如图所示的竖向张贴的海报,要求版心面积为128dm2,上、下两边各空2dm,左、右两边各空1dm。如何设计海报的尺寸,才能使四周空白面积最小?例2:某制造商制造并出售球形瓶装饮料.瓶子制造成本是0.8πr2分.已知每出售1ml的饮料,可获利0.2分,且瓶子的最大半径为6cm.1)瓶子半径多大时,能使每瓶饮料的 利润最大?
2)瓶子半径多大时,每瓶饮料的利润最小?问题2: 饮料瓶大小对饮料公司利润有影响吗?1.半径为2cm 时,利润最小,这时 表示此种瓶内饮料的
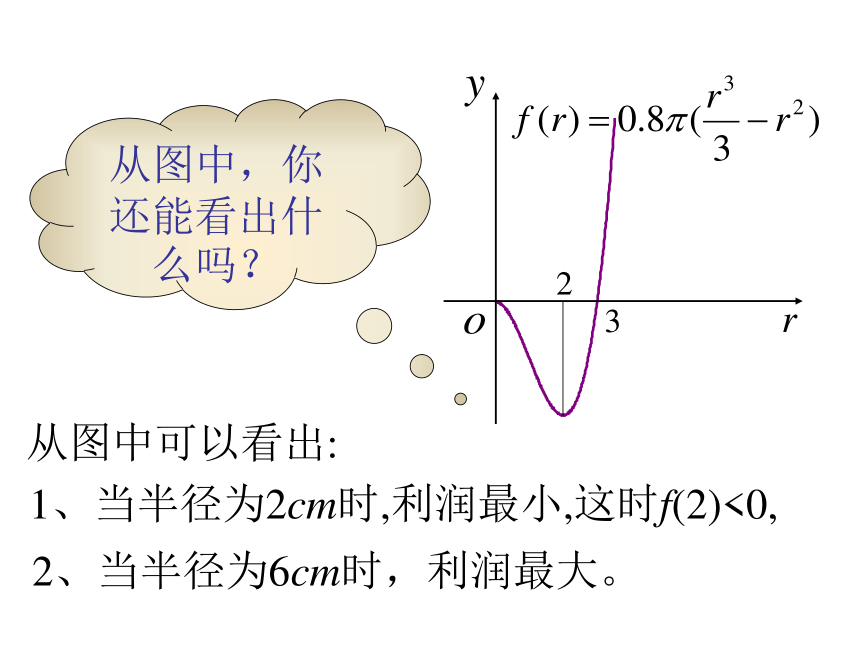
利润还不够瓶子的成本,此时利润是负值2.半径为6cm时,利润最大1、当半径为2cm时,利润最小,这时f(2)<0,2、当半径为6cm时,利润最大。从图中可以看出:从图中,你还能看出什么吗?问题3、磁盘的最大存储量问题(1) 你知道计算机是如何存储、检索信息的吗?
(2) 你知道磁盘的结构吗?(3)如何使一个圆环状的磁盘存储尽可能多的信息?例3:现有一张半径为R 的磁盘,它的存储区是半径介于r 与R 的环行区域。是不是r越小,磁盘的存储量越大?(2) r为多少时,磁盘具有最大存储量
(最外面的磁道不存储任何信息)?解:存储量=磁道数×每磁道的比特数(1) 它是一个关于r的二次函数,从函数的解析式可以判断,不是r越小,磁盘的存储量越大。例4:某种圆柱形的饮料罐的容积一定时,如何确定它的高与底半径,使得所用材料最省?变式:当圆柱形金属饮料罐的表面积为定值S时,它的高与底面半径应怎样选取,才能使所用材料最省?课堂练习 1.用总长为14.8m的钢条制作一个长方体容器的框架,如果所制作的容器的底面的一边比另一边长0.5m,那么高为多少时容器的容积最大?并求出它的最大容积.
2.课本P104利用导数解决优化问题的基本思路:优化问题优化问题的答案
用函数表示的数学问题用导数解决数学问题回顾总结 解决优化问题的方法:通过搜集大量的统计数据,建立与其相应的数学模型,再通过研究相应函数的性质,提出优化方案,使问题得到解决.在这个过程中,导数往往是一个有利的工具。可导函数y=f(x)的导数y/与函数值和极值之间的关系为( )
A、导数y/由负变正,则函数y由减变为增,且有极大值
B、导数y/由负变正,则函数y由增变为减,且有极大值
C、导数y/由正变负,则函数y由增变为减,且有极小值
D、导数y/由正变负,则函数y由增变为减,且有极大值D学生活动A注意:数形结合以及原函数与导函数图像的区别.略解:(1)由图像可知:(2)注意:数形结合以及函数与方程思想的应用
学校或班级举行活动,通常需要张贴海报进行宣传。现让你设计一张如图所示的竖向张贴的海报,要求版心面积为128dm2,上、下两边各空2dm,左、右两边各空1dm。如何设计海报的尺寸,才能使四周空白面积最小?例2:某制造商制造并出售球形瓶装饮料.瓶子制造成本是0.8πr2分.已知每出售1ml的饮料,可获利0.2分,且瓶子的最大半径为6cm.1)瓶子半径多大时,能使每瓶饮料的 利润最大?
2)瓶子半径多大时,每瓶饮料的利润最小?问题2: 饮料瓶大小对饮料公司利润有影响吗?1.半径为2cm 时,利润最小,这时 表示此种瓶内饮料的
利润还不够瓶子的成本,此时利润是负值2.半径为6cm时,利润最大1、当半径为2cm时,利润最小,这时f(2)<0,2、当半径为6cm时,利润最大。从图中可以看出:从图中,你还能看出什么吗?问题3、磁盘的最大存储量问题(1) 你知道计算机是如何存储、检索信息的吗?
(2) 你知道磁盘的结构吗?(3)如何使一个圆环状的磁盘存储尽可能多的信息?例3:现有一张半径为R 的磁盘,它的存储区是半径介于r 与R 的环行区域。是不是r越小,磁盘的存储量越大?(2) r为多少时,磁盘具有最大存储量
(最外面的磁道不存储任何信息)?解:存储量=磁道数×每磁道的比特数(1) 它是一个关于r的二次函数,从函数的解析式可以判断,不是r越小,磁盘的存储量越大。例4:某种圆柱形的饮料罐的容积一定时,如何确定它的高与底半径,使得所用材料最省?变式:当圆柱形金属饮料罐的表面积为定值S时,它的高与底面半径应怎样选取,才能使所用材料最省?课堂练习 1.用总长为14.8m的钢条制作一个长方体容器的框架,如果所制作的容器的底面的一边比另一边长0.5m,那么高为多少时容器的容积最大?并求出它的最大容积.
2.课本P104利用导数解决优化问题的基本思路:优化问题优化问题的答案
用函数表示的数学问题用导数解决数学问题回顾总结 解决优化问题的方法:通过搜集大量的统计数据,建立与其相应的数学模型,再通过研究相应函数的性质,提出优化方案,使问题得到解决.在这个过程中,导数往往是一个有利的工具。可导函数y=f(x)的导数y/与函数值和极值之间的关系为( )
A、导数y/由负变正,则函数y由减变为增,且有极大值
B、导数y/由负变正,则函数y由增变为减,且有极大值
C、导数y/由正变负,则函数y由增变为减,且有极小值
D、导数y/由正变负,则函数y由增变为减,且有极大值D学生活动A注意:数形结合以及原函数与导函数图像的区别.略解:(1)由图像可知:(2)注意:数形结合以及函数与方程思想的应用
