七年级数学下册第七章《平面直角坐标系》单元检测试卷(含解析)
文档属性
| 名称 | 七年级数学下册第七章《平面直角坐标系》单元检测试卷(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-27 09:15:03 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
七年级数学下册第七章《平面直角坐标系》单元检测试卷(含解析)
选择题(本大题共有10个小题,每小题3分,共30分)
1 . 下列数据中,不能确定物体位置的是( )
A.1单元201号 B.南偏西 C.学院路11号 D.东经,北纬
点P(4,3)所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
如图所示,在正方形网格中有A,B,C三个点,若建立平面直角坐标系后,
点A的坐标为(2,1),点B的坐标为(1,﹣2),则点C的坐标为( )
A.(1,1) B.(﹣2,1) C.(﹣1,﹣2) D.(﹣2,﹣1)
已知点A(-1,-4),B(-1,3),则( )
A.A,B关于x轴对称 B.A,B关于y轴对称
C.直线AB平行于y轴 D.直线AB垂直于y轴
点A在第二象限,且距离x轴2个单位长度,距离y轴4个单位长度,则点A的坐标是( )
A.(﹣4,2) B.(﹣2,4) C.(4,﹣2) D.(2,﹣4)
如图,将三角形向右平移2个单位长度,再向上平移3个单位长度,
则平移后三个顶点的坐标分别是( )
A.(2,2),(3,4),(1,7) B.(2,2),(4,3),(1,7)
C.(-2,2),(3,4),(1,7) D.(2,-2),(4,3),(1,7)
7. 已知点P(2 - a,3a + 6)到两标轴距离相等,则点P的坐标为( )
A.(3,3) B.(6,-6) C.(3,3)或(6,-6) D.(3,-3)
8. 如图,将长为3的长方形放在平面直角坐标系中,若点,则A点的坐标为( )
A. B. C. D.
9 . 如图,坐标平面上有P,Q两点,其坐标分别为(5,a),(b,7),
根据图中P,Q两点的位置,则点(6-b,a-10)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
如图,在平面直角坐标系中,,,,
一只瓢虫从点出发以2个单位长度/秒的速度沿→→→→循环爬行,
则第2024秒瓢虫的位置在( )
A. B. C. D.
填空题(本大题共有10个小题,每小题4分,共40分)
11.七年级(2)班教室里的座位共有7排8列,其中小明的座位在第3排第7列,简记为(3,7),
小华坐在第5排第2列,则小华的座位可记作 .
12.直角坐标系中,第四象限内一点P到x轴的距离为2,到y轴的距离为5,那么点P的坐标是
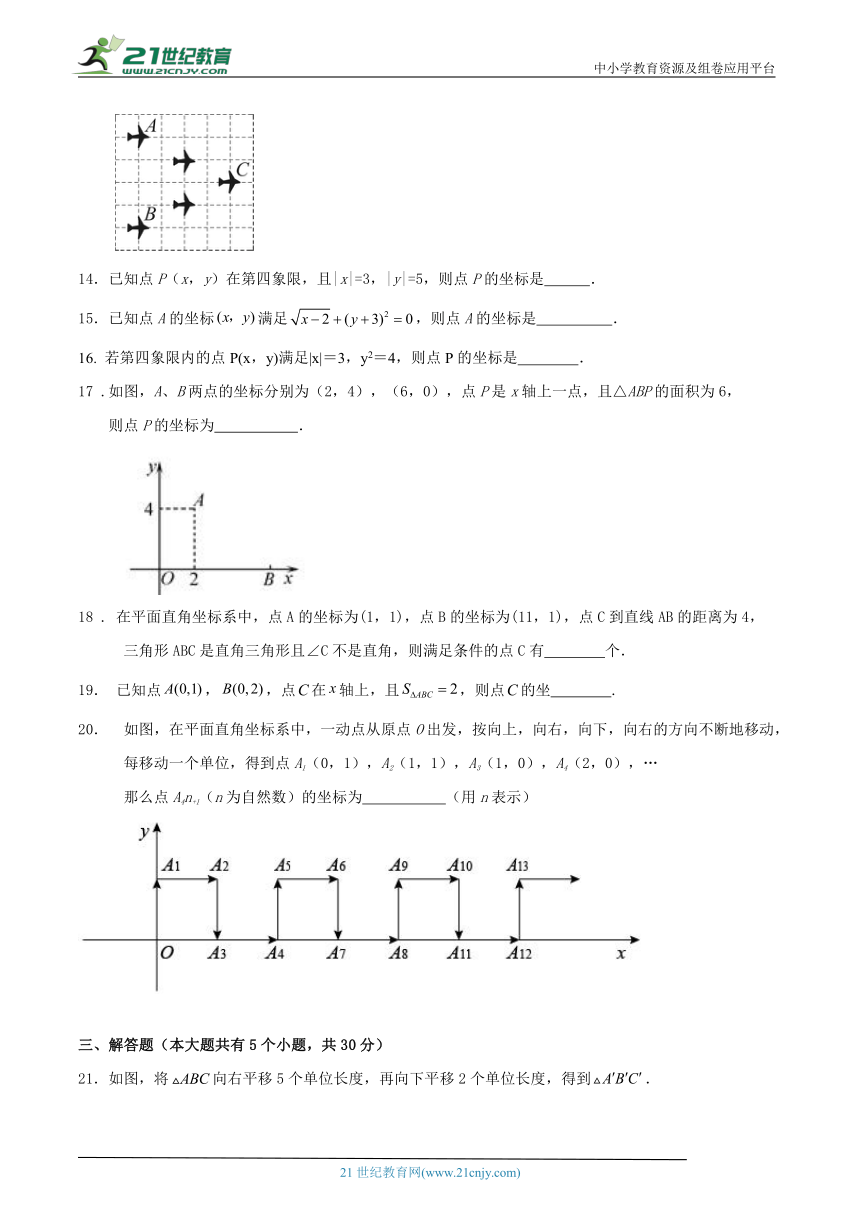
13 .如图是一个飞行队形,如果最后两架飞机的平面坐标分别为A(﹣2,1)和B(﹣2,﹣3),
那么第一架飞机C的平面坐标是 .
14.已知点P(x,y)在第四象限,且|x|=3,|y|=5,则点P的坐标是 .
15.已知点A的坐标满足,则点A的坐标是 .
16. 若第四象限内的点P(x,y)满足|x|=3,y2=4,则点P的坐标是 .
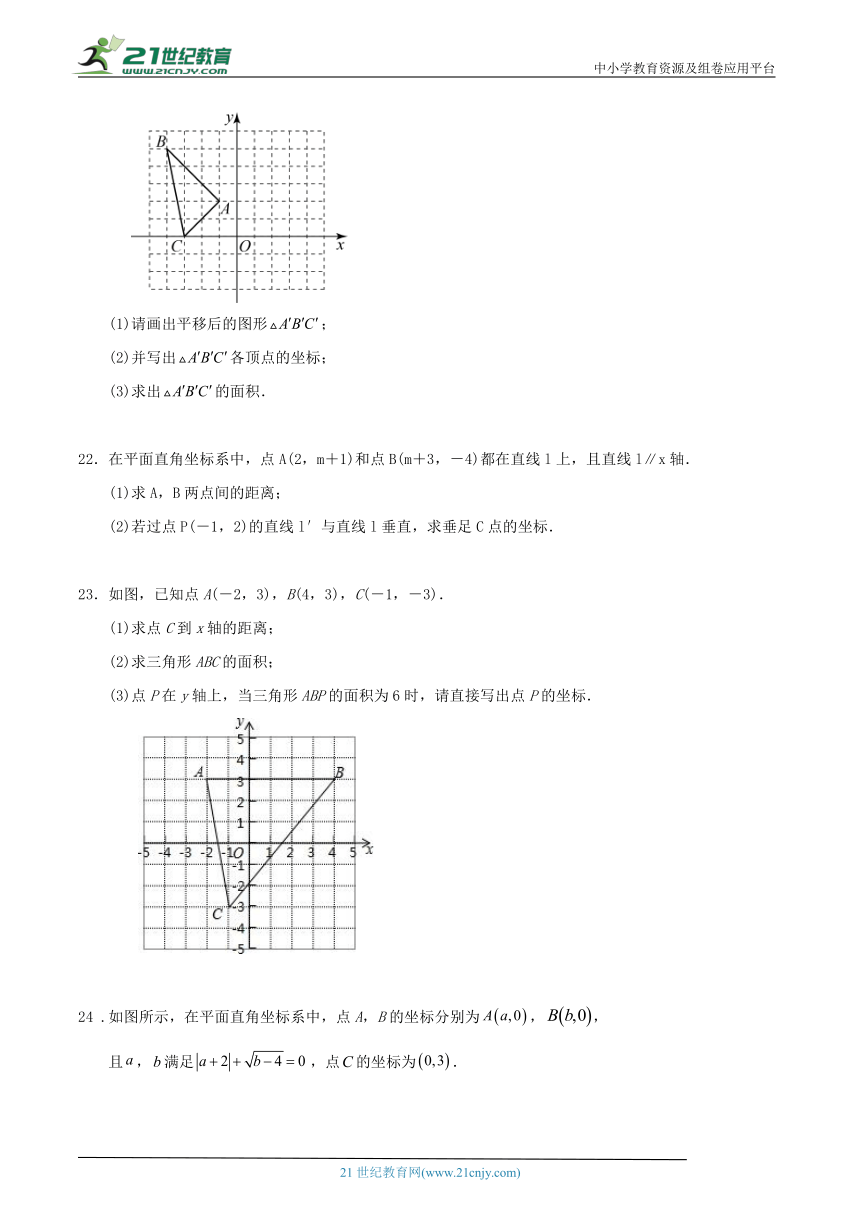
17 .如图,A、B两点的坐标分别为(2,4),(6,0),点P是x轴上一点,且△ABP的面积为6,
则点P的坐标为 .
18 . 在平面直角坐标系中,点A的坐标为(1,1),点B的坐标为(11,1),点C到直线AB的距离为4,
三角形ABC是直角三角形且∠C不是直角,则满足条件的点C有 个.
已知点,,点在轴上,且,则点的坐 .
如图,在平面直角坐标系中,一动点从原点O出发,按向上,向右,向下,向右的方向不断地移动,每移动一个单位,得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),…
那么点A4n+1(n为自然数)的坐标为 (用n表示)
三、解答题(本大题共有5个小题,共30分)
21.如图,将向右平移5个单位长度,再向下平移2个单位长度,得到.
(1)请画出平移后的图形;
(2)并写出各顶点的坐标;
(3)求出的面积.
22.在平面直角坐标系中,点A(2,m+1)和点B(m+3,-4)都在直线l上,且直线l∥x轴.
(1)求A,B两点间的距离;
(2)若过点P(-1,2)的直线l′与直线l垂直,求垂足C点的坐标.
23.如图,已知点A(-2,3),B(4,3),C(-1,-3).
(1)求点C到x轴的距离;
(2)求三角形ABC的面积;
(3)点P在y轴上,当三角形ABP的面积为6时,请直接写出点P的坐标.
24 .如图所示,在平面直角坐标系中,点A,B的坐标分别为,,
且,满足,点的坐标为.
(1)求,的值及;
(2)若点在轴上,且,试求点的坐标.
25 .如图,在平面直角坐标系中,已知点A(-3,3),B(-5,1),C(-2,0),
P(a,b)是△ABC的边AC上任意一点,△ABC经过平移后得到△A1B1C1,
点P的对应点为P1(a+6,b-2).
(1)直接写出点C1的坐标;
(2)在图中画出△A1B1C1;
(3)求△AOA1的面积.
七年级数学下册第七章《平面直角坐标系》单元检测试卷 解析
一、选择题(本大题共有10个小题,每小题3分,共30分)
1 .下列数据中,不能确定物体位置的是( )
A.1单元201号 B.南偏西 C.学院路11号 D.东经,北纬
【答案】B
【分析】确定一个物体的位置,要用一个有序数对,即用两个数据.找到一个数据的选项即为所求.
【详解】解:A、1单元201号,是有序数对,能确定物体的位置,故正确;
B、南偏西45°,不是有序数对,不能确定物体的位置,故错误;
C、学院路11号,“学院路”相当于一个数据,是有序数对,能确定物体的位置,故正确;
D、东经105°北纬40°,是有序数对,能确定物体的位置,故正确.
故选B.
2.点P(4,3)所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【答案】A
【详解】试题分析:因为点P(4,3)的横坐标是正数,纵坐标是正数,
所以点P在平面直角坐标系的第一象限.故选A.
考点:点的坐标.
3 .如图所示,在正方形网格中有A,B,C三个点,若建立平面直角坐标系后,
点A的坐标为(2,1),点B的坐标为(1,﹣2),则点C的坐标为( )
A.(1,1) B.(﹣2,1) C.(﹣1,﹣2) D.(﹣2,﹣1)
【答案】D
【分析】根据点A的坐标为(2,1),点B的坐标为(1,﹣2)可建立坐标系,进而问题可求解.
【详解】解:由点A的坐标为(2,1),点B的坐标为(1,﹣2)可建立如下坐标系:
∴点C的坐标为(﹣2,﹣1);
故选D.
4 . 已知点A(-1,-4),B(-1,3),则( )
A.A,B关于x轴对称 B.A,B关于y轴对称
C.直线AB平行于y轴 D.直线AB垂直于y轴
【答案】C
【详解】试题解析:∵点A(-1,-4),B(-1,3),
∴点A与点B的横坐标相同,纵坐标不同,
∴直线AB平行于y轴.
故选C.
5 . 点A在第二象限,且距离x轴2个单位长度,距离y轴4个单位长度,则点A的坐标是( )
A.(﹣4,2) B.(﹣2,4) C.(4,﹣2) D.(2,﹣4)
【答案】A
【分析】根据第二象限内点的横坐标是负数,纵坐标是正数,点到x轴的距离等于纵坐标的绝对值,到y轴的距离等于横坐标的绝对值解答.
【详解】∵点A在第二象限,且距离x轴2个单位长度,距离y轴4个单位长度,
∴点A的横坐标是﹣4,纵坐标是2,
∴点A的坐标为(﹣4,2).
故选A.
6 . 如图,将三角形向右平移2个单位长度,再向上平移3个单位长度,
则平移后三个顶点的坐标分别是( )
A.(2,2),(3,4),(1,7) B.(2,2),(4,3),(1,7)
C.(-2,2),(3,4),(1,7) D.(2,-2),(4,3),(1,7)
【答案】C
【分析】直接利用平移中点的变化规律:
①向右平移a个单位,坐标P(x,y) P(x+a,y);
②向左平移a个单位,坐标P(x,y) P(x-a,y);
③向上平移b个单位,坐标P(x,y) P(x,y+b);
④向下平移b个单位,坐标P(x,y) P(x,y-b);
将图中的三个点的坐标,根据上面的规律,横坐标加2,纵坐标加3,即可得到平移后的坐标.
【详解】由题意可知此题平移规律是:(x+2,y+3),
照此规律计算可知原三个顶点(-4,-1),(1,1),(-1,4),
平移后三个顶点的坐标是(-2,2),(3,4),(1,7).
故选C.
7.已知点P(2 - a,3a + 6)到两标轴距离相等,则点P的坐标为( )
A.(3,3) B.(6,-6)
C.(3,3)或(6,-6) D.(3,-3)
【答案】C
【分析】利用点P到x轴、y轴的距离相等,得出横纵坐标相等或互为相反数进而得出答案.
【详解】解∶∵点P(2 - a,3a + 6)到两标轴距离相等,
∴,
∴a=-1或-4,
∴点P坐标为(3,3)或(6,-6).
故选:C.
8.如图,将长为3的长方形放在平面直角坐标系中,若点,则A点的坐标为( )
A. B. C. D.
【答案】D
【分析】延长交y轴于点E,则轴.即有,
则A点的横坐标为3;根据轴,可得A点的纵坐标与D点的纵坐标相同,问题得解.
【详解】解:延长交y轴于点E,则轴.
∵,
∴A点的横坐标为3;
∵轴,
∴A点的纵坐标与D点的纵坐标相同,为3,
∴A点的坐标为.
故选:D.
9 .如图,坐标平面上有P,Q两点,其坐标分别为(5,a),(b,7),
根据图中P,Q两点的位置,则点(6-b,a-10)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【答案】D
【详解】∵(5,a)、(b,7),
∴a<7,b<5,
∴6-b>0,a-10<0,
∴点(6-b,a-10)在第四象限.
故选:D.
10 . 如图,在平面直角坐标系中,,,,
一只瓢虫从点出发以2个单位长度/秒的速度沿→→→→循环爬行,
则第2024秒瓢虫的位置在( )
A. B. C. D.
【答案】A
【分析】根据点,,,的坐标可得出,及四边形的周长,由,且,可得出当秒时,瓢虫上,且距离点2个单位,即可得出结论.
【详解】解:∵,,,,
∴,,
∴四边形的周长为,
∵瓢虫从点出发以2个单位长度/秒的速度沿→→→→循环爬行,
∴瓢虫爬行一个循环所用的时间为,
∵,且,
∴此时瓢虫在上,且距离点2个单位,
∴此时点瓢虫的坐标为(-1,-1).
故选:A.
填空题(本大题共有10个小题,每小题4分,共40分)
11.七年级(2)班教室里的座位共有7排8列,其中小明的座位在第3排第7列,简记为(3,7),
小华坐在第5排第2列,则小华的座位可记作 .
【答案】(5,2)
【分析】由已知条件知:横坐标表示第几排,纵坐标表示第几列.
【详解】解:由题意可知座位的表示方法为排在前,列在后,
得小华的座位可记作(5,2).
故答案为:(5,2).
12.直角坐标系中,第四象限内一点P到x轴的距离为2,到y轴的距离为5,那么点P的坐标是
【答案】(5,-2).
【详解】试题分析:根据第四象限点的横坐标是正数,纵坐标是负数,
点到x轴的距离等于纵坐标的长度,到y轴的距离等于横坐标的长度解答.
试题解析:∵第四象限内一点P到x轴的距离为2,到y轴的距离为5,
∴点P的横坐标是5,纵坐标是-2,
∴点P(5,-2).
13 .如图是一个飞行队形,如果最后两架飞机的平面坐标分别为A(﹣2,1)和B(﹣2,﹣3),
那么第一架飞机C的平面坐标是 .
【答案】(2,-1).
【详解】试题分析:如图,根据A(-2,1)和B(-2,-3)确定平面直角坐标系,然后根据点C在坐标系中的位置确定点C的坐标为(2,-1).
14.已知点P(x,y)在第四象限,且|x|=3,|y|=5,则点P的坐标是 .
【答案】(3,-5)
【分析】根据点在第四象限的坐标特点解答即可.
【详解】解:∵点P(x,y)在第四象限,
∴x>0,y<0,
又∵|x|=3,|y|=5,
∴x=3,y=﹣5,
∴点P的坐标是(3,﹣5),
故答案为:(3,﹣5).
15.已知点A的坐标满足,则点A的坐标是 .
【答案】
【分析】根据非负式子和为0它们分别等于0即可求解.
【详解】∵,且,,
∴ ,,
解得: ,,
故答案是:.
16. 若第四象限内的点P(x,y)满足|x|=3,y2=4,则点P的坐标是 .
【答案】(3,-2)
【详解】解:∵|x|=3,y2=4,
∴x=±3,y=±2,
∵点P(x,y)在第四象限,
∴x>0,y<0,
∴x=3,y=﹣2,
∴P点坐标为(3,﹣2).
故答案为:(3,﹣2).
17 .如图,A、B两点的坐标分别为(2,4),(6,0),点P是x轴上一点,且△ABP的面积为6,
则点P的坐标为 .
【答案】(3,0)或(9,0)
【详解】解:由题意可得△ABP的高为4,根据面积可得底为3,
∴BP=3,
∵B点的坐标为(6,0),
∴点P的坐标为(3,0)或(9,0).
故答案为:(3,0)或(9,0).
18 .在平面直角坐标系中,点A的坐标为(1,1),点B的坐标为(11,1),点C到直线AB的距离为4,
三角形ABC是直角三角形且∠C不是直角,则满足条件的点C有 个.
【答案】4
【详解】∵点A,B的纵坐标相等,
∴AB∥x轴,
∵点C到AB距离为4,
∴点C在平行于AB的两条直线上.
∴过点A的垂线与那两条直线有2个交点,
过点B的垂线与那两条直线有2个交点.
∴满足条件的C点共4个.
故答案是:4.
19.已知点,,点在轴上,且,则点的坐 .
【答案】或
【分析】根据点、的坐标求出,再根据三角形的面积求出的长,然后写出点的坐标即可.
【详解】解:,,
,
点在轴上,
,
解得.
点的坐标为或.
20 . 如图,在平面直角坐标系中,一动点从原点O出发,按向上,向右,向下,向右的方向不断地移动,
每移动一个单位,得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),…
那么点A4n+1(n为自然数)的坐标为 (用n表示)
【答案】(2n,1)
【分析】根据图形分别求出n=1、2、3时对应的点A4n+1的坐标,然后根据变化规律写出即可
【详解】由图可知,n=1时,4×1+1=5,点A5(2,1),
n=2时,4×2+1=9,点A9(4,1),
n=3时,4×3+1=13,点A13(6,1),
∴点A4n+1(2n,1).
故答案为:(2n,1)
三、解答题(本大题共有5个小题,共30分)
21.如图,将向右平移5个单位长度,再向下平移2个单位长度,得到.
(1)请画出平移后的图形;
(2)并写出各顶点的坐标;
(3)求出的面积.
【答案】(1)见解析
(2),,;
(3)的面积为6.
【分析】(1)先根据平移的分式确定的位置,再将其两两连线,即可;
(2)根据(1)的图形即可求解;
(3)利用割补法求解即可.
【详解】(1)解:如图:即为所求
;
(2)解:由(1)中的图形,可得,,;
(3)解:,
即的面积为6.
22.在平面直角坐标系中,点A(2,m+1)和点B(m+3,-4)都在直线l上,且直线l∥x轴.
(1)求A,B两点间的距离;
(2)若过点P(-1,2)的直线l′与直线l垂直,求垂足C点的坐标.
【答案】(1)4(2) C(-1,-4)
【详解】试题分析:(1)利用与x轴平行的直线上所有点的纵坐标相同得到m+1=-4,解得m=-5,易得A(2,-4),B(-2,-4),计算A,B两点间的横坐标之差即可;
(2)由于直线l′与直线l垂直于点C,则直线l′平行y轴,于是可得C点的横坐标为-1,加上直线l上的纵坐标都为-4,于是可得C点坐标.
试题解析:
(1)∵l∥x轴,点A,B都在l上,
∴m+1=-4,
∴m=-5,
∴A(2,-4),B(-2,-4),
∴A,B两点间的距离为4.
(2)∵l∥x轴,PC⊥l,x轴⊥y轴,
∴PC∥y轴,
∴C点横坐标为-1.又点C在l上,
∴C(-1,-4).
23.如图,已知点A(-2,3),B(4,3),C(-1,-3).
(1)求点C到x轴的距离;
(2)求三角形ABC的面积;
(3)点P在y轴上,当三角形ABP的面积为6时,请直接写出点P的坐标.
【答案】(1)3;(2)18;(3)(0,5)或(0,1).
【分析】(1)点C的纵坐标的绝对值就是点C到x轴的距离解答;
(2)根据三角形的面积公式列式进行计算即可求解;
(3)设点P的坐标为(0,y),根据△ABP的面积为6,A( 2,3)、B(4,3),所以×6×|x 3|=6,即|x 3|=2,所以x=5或x=1,即可解答.
【详解】解∶(1)∵C( 1, 3),
∴| 3|=3,
∴点C到x轴的距离为3;
(2)∵A( 2,3)、B(4,3)、C( 1, 3)
∴AB=4 ( 2) =6,点C到边AB的距离为:3 ( 3) =6,
∴△ABC的面积为:6×6÷2=18.
(3)设点P的坐标为(0,y),
∵△ABP的面积为6,A( 2,3)、B(4,3),
∴×6×|x 3|=6,
∴|x 3|=2,
∴x=5或x=1,
∴P点的坐标为(0,5)或(0,1).
24 .如图所示,在平面直角坐标系中,点A,B的坐标分别为,,
且,满足,点的坐标为.
(1)求,的值及;
(2)若点在轴上,且,试求点的坐标.
【答案】(1),,
(2)点的坐标为或
【分析】(1)由非负数的性质可求得a与b的值,则可得点A与B的坐标,从而求得AB的长,由已知可得CO的长,因此可求得△ABC的面积;
(2)设点的坐标为,则可得AM的长度,由题目中的面积关系可得关于x的方程,解方程即可求得x的值,从而求得点M的坐标.
【详解】(1)∵,
∴,,
∴,,
∴点,点.
又∵点,
∴,,
∴.
(2)设点的坐标为,则,
又∵,
∴,
∴,
∴,
即,
解得:或,
故点的坐标为或.
25 .如图,在平面直角坐标系中,已知点A(-3,3),B(-5,1),C(-2,0),
P(a,b)是△ABC的边AC上任意一点,△ABC经过平移后得到△A1B1C1,
点P的对应点为P1(a+6,b-2).
(1)直接写出点C1的坐标;
(2)在图中画出△A1B1C1;
(3)求△AOA1的面积.
【答案】(1)(4,-2);(2)作图见解析,(3)6.
【分析】(1)根据点P的对应点为P1()确定出平移规律为向右6个单位,向下2个单位,,由此规律和C(-2,0)即可求出C1的坐标;(2)根据(1)中的平移规律确定点A、B、C平移后的对应点A1、B1、C1的位置,然后顺次连接即可;(3)利用△AOA1所在的矩形的面积减去四周三个小直角三角形的面积,列式计算即可得解.
【详解】(1)∵点P(a,b)的对应点为P1(a+6,b-2),
∴平移规律为向右6个单位,向下2个单位,
∴C(-2,0)的对应点C1的坐标为(4,-2);
(2)△A1B1C1如图所示;
(3)△AOA1的面积=6×3-×3×3-×3×1-×6×2=18---6=18-12=6.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
七年级数学下册第七章《平面直角坐标系》单元检测试卷(含解析)
选择题(本大题共有10个小题,每小题3分,共30分)
1 . 下列数据中,不能确定物体位置的是( )
A.1单元201号 B.南偏西 C.学院路11号 D.东经,北纬
点P(4,3)所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
如图所示,在正方形网格中有A,B,C三个点,若建立平面直角坐标系后,
点A的坐标为(2,1),点B的坐标为(1,﹣2),则点C的坐标为( )
A.(1,1) B.(﹣2,1) C.(﹣1,﹣2) D.(﹣2,﹣1)
已知点A(-1,-4),B(-1,3),则( )
A.A,B关于x轴对称 B.A,B关于y轴对称
C.直线AB平行于y轴 D.直线AB垂直于y轴
点A在第二象限,且距离x轴2个单位长度,距离y轴4个单位长度,则点A的坐标是( )
A.(﹣4,2) B.(﹣2,4) C.(4,﹣2) D.(2,﹣4)
如图,将三角形向右平移2个单位长度,再向上平移3个单位长度,
则平移后三个顶点的坐标分别是( )
A.(2,2),(3,4),(1,7) B.(2,2),(4,3),(1,7)
C.(-2,2),(3,4),(1,7) D.(2,-2),(4,3),(1,7)
7. 已知点P(2 - a,3a + 6)到两标轴距离相等,则点P的坐标为( )
A.(3,3) B.(6,-6) C.(3,3)或(6,-6) D.(3,-3)
8. 如图,将长为3的长方形放在平面直角坐标系中,若点,则A点的坐标为( )
A. B. C. D.
9 . 如图,坐标平面上有P,Q两点,其坐标分别为(5,a),(b,7),
根据图中P,Q两点的位置,则点(6-b,a-10)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
如图,在平面直角坐标系中,,,,
一只瓢虫从点出发以2个单位长度/秒的速度沿→→→→循环爬行,
则第2024秒瓢虫的位置在( )
A. B. C. D.
填空题(本大题共有10个小题,每小题4分,共40分)
11.七年级(2)班教室里的座位共有7排8列,其中小明的座位在第3排第7列,简记为(3,7),
小华坐在第5排第2列,则小华的座位可记作 .
12.直角坐标系中,第四象限内一点P到x轴的距离为2,到y轴的距离为5,那么点P的坐标是
13 .如图是一个飞行队形,如果最后两架飞机的平面坐标分别为A(﹣2,1)和B(﹣2,﹣3),
那么第一架飞机C的平面坐标是 .
14.已知点P(x,y)在第四象限,且|x|=3,|y|=5,则点P的坐标是 .
15.已知点A的坐标满足,则点A的坐标是 .
16. 若第四象限内的点P(x,y)满足|x|=3,y2=4,则点P的坐标是 .
17 .如图,A、B两点的坐标分别为(2,4),(6,0),点P是x轴上一点,且△ABP的面积为6,
则点P的坐标为 .
18 . 在平面直角坐标系中,点A的坐标为(1,1),点B的坐标为(11,1),点C到直线AB的距离为4,
三角形ABC是直角三角形且∠C不是直角,则满足条件的点C有 个.
已知点,,点在轴上,且,则点的坐 .
如图,在平面直角坐标系中,一动点从原点O出发,按向上,向右,向下,向右的方向不断地移动,每移动一个单位,得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),…
那么点A4n+1(n为自然数)的坐标为 (用n表示)
三、解答题(本大题共有5个小题,共30分)
21.如图,将向右平移5个单位长度,再向下平移2个单位长度,得到.
(1)请画出平移后的图形;
(2)并写出各顶点的坐标;
(3)求出的面积.
22.在平面直角坐标系中,点A(2,m+1)和点B(m+3,-4)都在直线l上,且直线l∥x轴.
(1)求A,B两点间的距离;
(2)若过点P(-1,2)的直线l′与直线l垂直,求垂足C点的坐标.
23.如图,已知点A(-2,3),B(4,3),C(-1,-3).
(1)求点C到x轴的距离;
(2)求三角形ABC的面积;
(3)点P在y轴上,当三角形ABP的面积为6时,请直接写出点P的坐标.
24 .如图所示,在平面直角坐标系中,点A,B的坐标分别为,,
且,满足,点的坐标为.
(1)求,的值及;
(2)若点在轴上,且,试求点的坐标.
25 .如图,在平面直角坐标系中,已知点A(-3,3),B(-5,1),C(-2,0),
P(a,b)是△ABC的边AC上任意一点,△ABC经过平移后得到△A1B1C1,
点P的对应点为P1(a+6,b-2).
(1)直接写出点C1的坐标;
(2)在图中画出△A1B1C1;
(3)求△AOA1的面积.
七年级数学下册第七章《平面直角坐标系》单元检测试卷 解析
一、选择题(本大题共有10个小题,每小题3分,共30分)
1 .下列数据中,不能确定物体位置的是( )
A.1单元201号 B.南偏西 C.学院路11号 D.东经,北纬
【答案】B
【分析】确定一个物体的位置,要用一个有序数对,即用两个数据.找到一个数据的选项即为所求.
【详解】解:A、1单元201号,是有序数对,能确定物体的位置,故正确;
B、南偏西45°,不是有序数对,不能确定物体的位置,故错误;
C、学院路11号,“学院路”相当于一个数据,是有序数对,能确定物体的位置,故正确;
D、东经105°北纬40°,是有序数对,能确定物体的位置,故正确.
故选B.
2.点P(4,3)所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【答案】A
【详解】试题分析:因为点P(4,3)的横坐标是正数,纵坐标是正数,
所以点P在平面直角坐标系的第一象限.故选A.
考点:点的坐标.
3 .如图所示,在正方形网格中有A,B,C三个点,若建立平面直角坐标系后,
点A的坐标为(2,1),点B的坐标为(1,﹣2),则点C的坐标为( )
A.(1,1) B.(﹣2,1) C.(﹣1,﹣2) D.(﹣2,﹣1)
【答案】D
【分析】根据点A的坐标为(2,1),点B的坐标为(1,﹣2)可建立坐标系,进而问题可求解.
【详解】解:由点A的坐标为(2,1),点B的坐标为(1,﹣2)可建立如下坐标系:
∴点C的坐标为(﹣2,﹣1);
故选D.
4 . 已知点A(-1,-4),B(-1,3),则( )
A.A,B关于x轴对称 B.A,B关于y轴对称
C.直线AB平行于y轴 D.直线AB垂直于y轴
【答案】C
【详解】试题解析:∵点A(-1,-4),B(-1,3),
∴点A与点B的横坐标相同,纵坐标不同,
∴直线AB平行于y轴.
故选C.
5 . 点A在第二象限,且距离x轴2个单位长度,距离y轴4个单位长度,则点A的坐标是( )
A.(﹣4,2) B.(﹣2,4) C.(4,﹣2) D.(2,﹣4)
【答案】A
【分析】根据第二象限内点的横坐标是负数,纵坐标是正数,点到x轴的距离等于纵坐标的绝对值,到y轴的距离等于横坐标的绝对值解答.
【详解】∵点A在第二象限,且距离x轴2个单位长度,距离y轴4个单位长度,
∴点A的横坐标是﹣4,纵坐标是2,
∴点A的坐标为(﹣4,2).
故选A.
6 . 如图,将三角形向右平移2个单位长度,再向上平移3个单位长度,
则平移后三个顶点的坐标分别是( )
A.(2,2),(3,4),(1,7) B.(2,2),(4,3),(1,7)
C.(-2,2),(3,4),(1,7) D.(2,-2),(4,3),(1,7)
【答案】C
【分析】直接利用平移中点的变化规律:
①向右平移a个单位,坐标P(x,y) P(x+a,y);
②向左平移a个单位,坐标P(x,y) P(x-a,y);
③向上平移b个单位,坐标P(x,y) P(x,y+b);
④向下平移b个单位,坐标P(x,y) P(x,y-b);
将图中的三个点的坐标,根据上面的规律,横坐标加2,纵坐标加3,即可得到平移后的坐标.
【详解】由题意可知此题平移规律是:(x+2,y+3),
照此规律计算可知原三个顶点(-4,-1),(1,1),(-1,4),
平移后三个顶点的坐标是(-2,2),(3,4),(1,7).
故选C.
7.已知点P(2 - a,3a + 6)到两标轴距离相等,则点P的坐标为( )
A.(3,3) B.(6,-6)
C.(3,3)或(6,-6) D.(3,-3)
【答案】C
【分析】利用点P到x轴、y轴的距离相等,得出横纵坐标相等或互为相反数进而得出答案.
【详解】解∶∵点P(2 - a,3a + 6)到两标轴距离相等,
∴,
∴a=-1或-4,
∴点P坐标为(3,3)或(6,-6).
故选:C.
8.如图,将长为3的长方形放在平面直角坐标系中,若点,则A点的坐标为( )
A. B. C. D.
【答案】D
【分析】延长交y轴于点E,则轴.即有,
则A点的横坐标为3;根据轴,可得A点的纵坐标与D点的纵坐标相同,问题得解.
【详解】解:延长交y轴于点E,则轴.
∵,
∴A点的横坐标为3;
∵轴,
∴A点的纵坐标与D点的纵坐标相同,为3,
∴A点的坐标为.
故选:D.
9 .如图,坐标平面上有P,Q两点,其坐标分别为(5,a),(b,7),
根据图中P,Q两点的位置,则点(6-b,a-10)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【答案】D
【详解】∵(5,a)、(b,7),
∴a<7,b<5,
∴6-b>0,a-10<0,
∴点(6-b,a-10)在第四象限.
故选:D.
10 . 如图,在平面直角坐标系中,,,,
一只瓢虫从点出发以2个单位长度/秒的速度沿→→→→循环爬行,
则第2024秒瓢虫的位置在( )
A. B. C. D.
【答案】A
【分析】根据点,,,的坐标可得出,及四边形的周长,由,且,可得出当秒时,瓢虫上,且距离点2个单位,即可得出结论.
【详解】解:∵,,,,
∴,,
∴四边形的周长为,
∵瓢虫从点出发以2个单位长度/秒的速度沿→→→→循环爬行,
∴瓢虫爬行一个循环所用的时间为,
∵,且,
∴此时瓢虫在上,且距离点2个单位,
∴此时点瓢虫的坐标为(-1,-1).
故选:A.
填空题(本大题共有10个小题,每小题4分,共40分)
11.七年级(2)班教室里的座位共有7排8列,其中小明的座位在第3排第7列,简记为(3,7),
小华坐在第5排第2列,则小华的座位可记作 .
【答案】(5,2)
【分析】由已知条件知:横坐标表示第几排,纵坐标表示第几列.
【详解】解:由题意可知座位的表示方法为排在前,列在后,
得小华的座位可记作(5,2).
故答案为:(5,2).
12.直角坐标系中,第四象限内一点P到x轴的距离为2,到y轴的距离为5,那么点P的坐标是
【答案】(5,-2).
【详解】试题分析:根据第四象限点的横坐标是正数,纵坐标是负数,
点到x轴的距离等于纵坐标的长度,到y轴的距离等于横坐标的长度解答.
试题解析:∵第四象限内一点P到x轴的距离为2,到y轴的距离为5,
∴点P的横坐标是5,纵坐标是-2,
∴点P(5,-2).
13 .如图是一个飞行队形,如果最后两架飞机的平面坐标分别为A(﹣2,1)和B(﹣2,﹣3),
那么第一架飞机C的平面坐标是 .
【答案】(2,-1).
【详解】试题分析:如图,根据A(-2,1)和B(-2,-3)确定平面直角坐标系,然后根据点C在坐标系中的位置确定点C的坐标为(2,-1).
14.已知点P(x,y)在第四象限,且|x|=3,|y|=5,则点P的坐标是 .
【答案】(3,-5)
【分析】根据点在第四象限的坐标特点解答即可.
【详解】解:∵点P(x,y)在第四象限,
∴x>0,y<0,
又∵|x|=3,|y|=5,
∴x=3,y=﹣5,
∴点P的坐标是(3,﹣5),
故答案为:(3,﹣5).
15.已知点A的坐标满足,则点A的坐标是 .
【答案】
【分析】根据非负式子和为0它们分别等于0即可求解.
【详解】∵,且,,
∴ ,,
解得: ,,
故答案是:.
16. 若第四象限内的点P(x,y)满足|x|=3,y2=4,则点P的坐标是 .
【答案】(3,-2)
【详解】解:∵|x|=3,y2=4,
∴x=±3,y=±2,
∵点P(x,y)在第四象限,
∴x>0,y<0,
∴x=3,y=﹣2,
∴P点坐标为(3,﹣2).
故答案为:(3,﹣2).
17 .如图,A、B两点的坐标分别为(2,4),(6,0),点P是x轴上一点,且△ABP的面积为6,
则点P的坐标为 .
【答案】(3,0)或(9,0)
【详解】解:由题意可得△ABP的高为4,根据面积可得底为3,
∴BP=3,
∵B点的坐标为(6,0),
∴点P的坐标为(3,0)或(9,0).
故答案为:(3,0)或(9,0).
18 .在平面直角坐标系中,点A的坐标为(1,1),点B的坐标为(11,1),点C到直线AB的距离为4,
三角形ABC是直角三角形且∠C不是直角,则满足条件的点C有 个.
【答案】4
【详解】∵点A,B的纵坐标相等,
∴AB∥x轴,
∵点C到AB距离为4,
∴点C在平行于AB的两条直线上.
∴过点A的垂线与那两条直线有2个交点,
过点B的垂线与那两条直线有2个交点.
∴满足条件的C点共4个.
故答案是:4.
19.已知点,,点在轴上,且,则点的坐 .
【答案】或
【分析】根据点、的坐标求出,再根据三角形的面积求出的长,然后写出点的坐标即可.
【详解】解:,,
,
点在轴上,
,
解得.
点的坐标为或.
20 . 如图,在平面直角坐标系中,一动点从原点O出发,按向上,向右,向下,向右的方向不断地移动,
每移动一个单位,得到点A1(0,1),A2(1,1),A3(1,0),A4(2,0),…
那么点A4n+1(n为自然数)的坐标为 (用n表示)
【答案】(2n,1)
【分析】根据图形分别求出n=1、2、3时对应的点A4n+1的坐标,然后根据变化规律写出即可
【详解】由图可知,n=1时,4×1+1=5,点A5(2,1),
n=2时,4×2+1=9,点A9(4,1),
n=3时,4×3+1=13,点A13(6,1),
∴点A4n+1(2n,1).
故答案为:(2n,1)
三、解答题(本大题共有5个小题,共30分)
21.如图,将向右平移5个单位长度,再向下平移2个单位长度,得到.
(1)请画出平移后的图形;
(2)并写出各顶点的坐标;
(3)求出的面积.
【答案】(1)见解析
(2),,;
(3)的面积为6.
【分析】(1)先根据平移的分式确定的位置,再将其两两连线,即可;
(2)根据(1)的图形即可求解;
(3)利用割补法求解即可.
【详解】(1)解:如图:即为所求
;
(2)解:由(1)中的图形,可得,,;
(3)解:,
即的面积为6.
22.在平面直角坐标系中,点A(2,m+1)和点B(m+3,-4)都在直线l上,且直线l∥x轴.
(1)求A,B两点间的距离;
(2)若过点P(-1,2)的直线l′与直线l垂直,求垂足C点的坐标.
【答案】(1)4(2) C(-1,-4)
【详解】试题分析:(1)利用与x轴平行的直线上所有点的纵坐标相同得到m+1=-4,解得m=-5,易得A(2,-4),B(-2,-4),计算A,B两点间的横坐标之差即可;
(2)由于直线l′与直线l垂直于点C,则直线l′平行y轴,于是可得C点的横坐标为-1,加上直线l上的纵坐标都为-4,于是可得C点坐标.
试题解析:
(1)∵l∥x轴,点A,B都在l上,
∴m+1=-4,
∴m=-5,
∴A(2,-4),B(-2,-4),
∴A,B两点间的距离为4.
(2)∵l∥x轴,PC⊥l,x轴⊥y轴,
∴PC∥y轴,
∴C点横坐标为-1.又点C在l上,
∴C(-1,-4).
23.如图,已知点A(-2,3),B(4,3),C(-1,-3).
(1)求点C到x轴的距离;
(2)求三角形ABC的面积;
(3)点P在y轴上,当三角形ABP的面积为6时,请直接写出点P的坐标.
【答案】(1)3;(2)18;(3)(0,5)或(0,1).
【分析】(1)点C的纵坐标的绝对值就是点C到x轴的距离解答;
(2)根据三角形的面积公式列式进行计算即可求解;
(3)设点P的坐标为(0,y),根据△ABP的面积为6,A( 2,3)、B(4,3),所以×6×|x 3|=6,即|x 3|=2,所以x=5或x=1,即可解答.
【详解】解∶(1)∵C( 1, 3),
∴| 3|=3,
∴点C到x轴的距离为3;
(2)∵A( 2,3)、B(4,3)、C( 1, 3)
∴AB=4 ( 2) =6,点C到边AB的距离为:3 ( 3) =6,
∴△ABC的面积为:6×6÷2=18.
(3)设点P的坐标为(0,y),
∵△ABP的面积为6,A( 2,3)、B(4,3),
∴×6×|x 3|=6,
∴|x 3|=2,
∴x=5或x=1,
∴P点的坐标为(0,5)或(0,1).
24 .如图所示,在平面直角坐标系中,点A,B的坐标分别为,,
且,满足,点的坐标为.
(1)求,的值及;
(2)若点在轴上,且,试求点的坐标.
【答案】(1),,
(2)点的坐标为或
【分析】(1)由非负数的性质可求得a与b的值,则可得点A与B的坐标,从而求得AB的长,由已知可得CO的长,因此可求得△ABC的面积;
(2)设点的坐标为,则可得AM的长度,由题目中的面积关系可得关于x的方程,解方程即可求得x的值,从而求得点M的坐标.
【详解】(1)∵,
∴,,
∴,,
∴点,点.
又∵点,
∴,,
∴.
(2)设点的坐标为,则,
又∵,
∴,
∴,
∴,
即,
解得:或,
故点的坐标为或.
25 .如图,在平面直角坐标系中,已知点A(-3,3),B(-5,1),C(-2,0),
P(a,b)是△ABC的边AC上任意一点,△ABC经过平移后得到△A1B1C1,
点P的对应点为P1(a+6,b-2).
(1)直接写出点C1的坐标;
(2)在图中画出△A1B1C1;
(3)求△AOA1的面积.
【答案】(1)(4,-2);(2)作图见解析,(3)6.
【分析】(1)根据点P的对应点为P1()确定出平移规律为向右6个单位,向下2个单位,,由此规律和C(-2,0)即可求出C1的坐标;(2)根据(1)中的平移规律确定点A、B、C平移后的对应点A1、B1、C1的位置,然后顺次连接即可;(3)利用△AOA1所在的矩形的面积减去四周三个小直角三角形的面积,列式计算即可得解.
【详解】(1)∵点P(a,b)的对应点为P1(a+6,b-2),
∴平移规律为向右6个单位,向下2个单位,
∴C(-2,0)的对应点C1的坐标为(4,-2);
(2)△A1B1C1如图所示;
(3)△AOA1的面积=6×3-×3×3-×3×1-×6×2=18---6=18-12=6.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
