初中数学北师大版八年级上册《4.3.2一次例函数的图象与性质》教学设计(表格式)
文档属性
| 名称 | 初中数学北师大版八年级上册《4.3.2一次例函数的图象与性质》教学设计(表格式) |

|
|
| 格式 | doc | ||
| 文件大小 | 758.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-19 00:00:00 | ||
图片预览


文档简介
北师大版八年级数学(上)第四章《一次函数》
课题 4.3.2一次例函数的图象与性质 课 时 1
教学目标 知识与技能 1.会用描点法画一次函数的图象,理解两点法可快速画一次函数的图象。2.掌握一次函数图象的特点及其性质。3.能用一次函数的图象性质解决相关问题。
过程与方法 经历函数图象的作图过程,初步了解作函数图象的一般步骤,理解一次函数的关系式与图象之间的对应关系。
情感态度与价值观 能熟练作出一次函数的图象,掌握一次函数图象的特点及其性质。
教法 引导发现为主,直观演示相结合。
重点 能熟练地画出一次函数的图象并掌握其性质。
难点 理解一次函数的表达式与图象之间的对应关系。
课 前 准 备
教 具 学 具
教师活动(集体共备) 学生活动
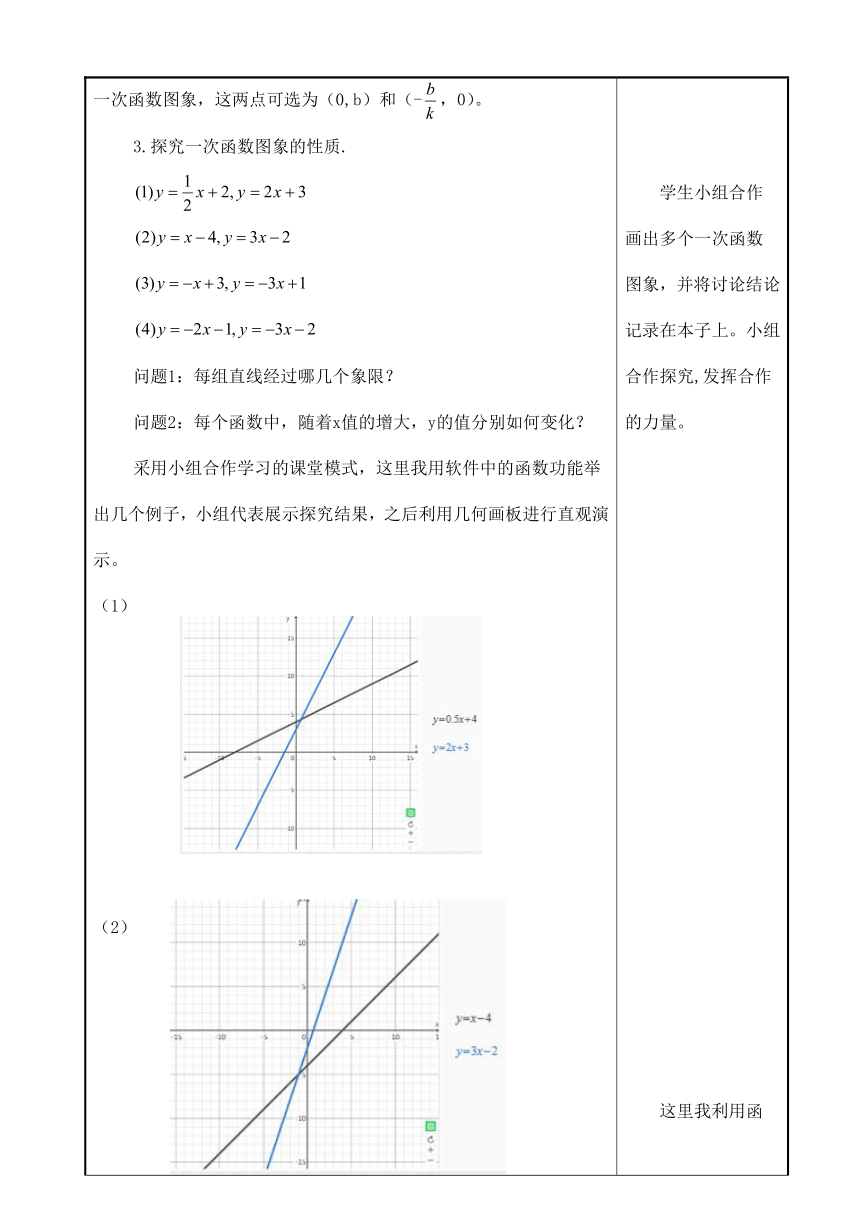
1、检查预习单课前我推送给学生的课前预习任务单,学生借助预习单探索出一次函数图象的画法。复习回顾利用思维导图回忆正比例函数的表达式,图象及性质,类比正比例函数的探究过程探究一次函数。3、合作交流、探究学习1.画出一次函数y=2x+2与y=2x+3图象(利用微课进行描点法回顾)(1)列表.x…-2-1012…y=2x+2……y=2x+3…… (2)描点:用表里各组对应值作为点的坐标,在直角坐标系内描出相应的点.(3)连线:把这些点依次连接起来,得到图象.(利用101PPT函数功能)小结:画函数图象的一般步骤:列表、描点、连线.思考:函数的自变量的值和所对应的函数值有多少对?这些值作为点的坐标可以描出多少点呢?这些点可以构成什么图形?一系列问题充分调动学生思考力与想象力,并发现:一次函数的图象是一条直线.一次函数y=kx+b的图象也称为直线y=kx+b。2.如何快速画出一次函数的图象?学生思考后小结,两点确定一条直线,得到经过两点可快速画出一次函数图象,这两点可选为(0,b)和(-,0)。3.探究一次函数图象的性质. 问题1:每组直线经过哪几个象限?问题2:每个函数中,随着x值的增大,y的值分别如何变化?采用小组合作学习的课堂模式,这里我用软件中的函数功能举出几个例子,小组代表展示探究结果,之后利用几何画板进行直观演示。(1)(2)(3)(4)一次函数y=kx+b中的k、b与它的图象有什么关系?一次函数y=kx+b图象的增减性? 我利用课前学生在预习单设疑部分的填写,及时掌握学生不易理解之处,更有针对性的进行教学。我利用几何画板,让这个函数y=2x+2和y=2x+3图象自然生成,给学生提供思考和想象的空间。教师通过调节坐标系向学生展示这些点构成的图形。学生小组合作画出多个一次函数图象,并将讨论结论记录在本子上。小组合作探究,发挥合作的力量。这里我利用函数功能形象直观的为学生展示一次函数图象的增减性。给点设置动画,随着点从左到右逐渐上升,观察点的横坐标变化,点的纵坐标变化,最终得出结论。
我利用几何画板形象直观的为学生展示一次函数图象的增减性。 4.归纳性质:k>0,b>0时,函数图象经过第一、二、三象限。k>0,b<0时,函数图象经过第一、三、四象限。k<0,b>0时,函数图象经过第一、二、四象限。k<0,b<0时,函数图象经过第二、三、四象限。当k>0时,图象从左向右上升,y随x的增大而增大.当k<0时,图象从左向右下降,y随x的增大而减小.此环节采用101PPT随机点名功能。5.插入游戏,采取小组加分制,调节课堂气氛。学以致用、巩固练习1.函数 y=2x-5中,y随x的增大而_____,它的图象与y轴的交点坐标是_____.它的图象与x轴的交点坐标是____.2.已知点A(-5,a),B(4,b)在直线上y=-3x+2,则a b(填“>”“<”或“=”).此题利用几何画板进行演示。3.一次函数y=kx+b的图象如图所示,你能说出b的值吗?4.已知函数 y = kx的图象经过第二、四象限,那么函数y = kx-k的图象可能是( ) 此环节利用101PPT计时五分钟,计时结束小组先互判,后小组代表讲解有问题的题目,教师进行补充。四、导图总结、分层作业课堂小结分两部分,首先是知识小结,先由学困生先做答,再由学优生补充,使每个学生都能参与课堂。最后利用思维导图总结,思维导图使知识点更加系统、有条理,便于学生理解、记忆。其次是方法小结,学生通过回顾,归纳函数研究的方面,为以后其他函数的学习指明方向和方法。布置作业,我设计了个性化的选做作业,学生根据自己的能力进行选择。一方面是习题的练习,一方面学生继续探究一次函数的图象,从而巩固所学,并延伸所学。 考虑到让没有参与的学生也能认真思考,提出问题:请大家找出出现问题的地方,回答正确的同学会有相应的加分。四道典型例题,巩固一次函数的图象及性质。第一题考察一次函数的性质掌握情况,第二题渗透解题的多种方法,代数法以及图象的法,第三、四题渗透数形结合思想。练习遵循由易到难,由简到繁而设计。学生自己进行小结,发挥主体地位,学生互相补充。
板书设计 4.3.2一次函数的图象与性质
反思 教学反思 本课的内容比较抽象,学生不易理解。因此课前我让学生完成课前预习任务单,帮助学生初步感知,增强学生自主探究意识。课上利用几何画板,101PPT学科工具进行直观展示,解决学生疑惑。四个教学环节就是四个台阶,帮助学生一步步达成学习目标,并渗透数形结合的数学思想。几何画板,101PPT学科工具的利用解决了传统课堂不易演示,立体感受限的问题,培养了学生的数学思想和空间想象能力,真正做到了以学生为本的课堂。
小组合作 小组合作较好,能共同解决疑惑。
课题 4.3.2一次例函数的图象与性质 课 时 1
教学目标 知识与技能 1.会用描点法画一次函数的图象,理解两点法可快速画一次函数的图象。2.掌握一次函数图象的特点及其性质。3.能用一次函数的图象性质解决相关问题。
过程与方法 经历函数图象的作图过程,初步了解作函数图象的一般步骤,理解一次函数的关系式与图象之间的对应关系。
情感态度与价值观 能熟练作出一次函数的图象,掌握一次函数图象的特点及其性质。
教法 引导发现为主,直观演示相结合。
重点 能熟练地画出一次函数的图象并掌握其性质。
难点 理解一次函数的表达式与图象之间的对应关系。
课 前 准 备
教 具 学 具
教师活动(集体共备) 学生活动
1、检查预习单课前我推送给学生的课前预习任务单,学生借助预习单探索出一次函数图象的画法。复习回顾利用思维导图回忆正比例函数的表达式,图象及性质,类比正比例函数的探究过程探究一次函数。3、合作交流、探究学习1.画出一次函数y=2x+2与y=2x+3图象(利用微课进行描点法回顾)(1)列表.x…-2-1012…y=2x+2……y=2x+3…… (2)描点:用表里各组对应值作为点的坐标,在直角坐标系内描出相应的点.(3)连线:把这些点依次连接起来,得到图象.(利用101PPT函数功能)小结:画函数图象的一般步骤:列表、描点、连线.思考:函数的自变量的值和所对应的函数值有多少对?这些值作为点的坐标可以描出多少点呢?这些点可以构成什么图形?一系列问题充分调动学生思考力与想象力,并发现:一次函数的图象是一条直线.一次函数y=kx+b的图象也称为直线y=kx+b。2.如何快速画出一次函数的图象?学生思考后小结,两点确定一条直线,得到经过两点可快速画出一次函数图象,这两点可选为(0,b)和(-,0)。3.探究一次函数图象的性质. 问题1:每组直线经过哪几个象限?问题2:每个函数中,随着x值的增大,y的值分别如何变化?采用小组合作学习的课堂模式,这里我用软件中的函数功能举出几个例子,小组代表展示探究结果,之后利用几何画板进行直观演示。(1)(2)(3)(4)一次函数y=kx+b中的k、b与它的图象有什么关系?一次函数y=kx+b图象的增减性? 我利用课前学生在预习单设疑部分的填写,及时掌握学生不易理解之处,更有针对性的进行教学。我利用几何画板,让这个函数y=2x+2和y=2x+3图象自然生成,给学生提供思考和想象的空间。教师通过调节坐标系向学生展示这些点构成的图形。学生小组合作画出多个一次函数图象,并将讨论结论记录在本子上。小组合作探究,发挥合作的力量。这里我利用函数功能形象直观的为学生展示一次函数图象的增减性。给点设置动画,随着点从左到右逐渐上升,观察点的横坐标变化,点的纵坐标变化,最终得出结论。
我利用几何画板形象直观的为学生展示一次函数图象的增减性。 4.归纳性质:k>0,b>0时,函数图象经过第一、二、三象限。k>0,b<0时,函数图象经过第一、三、四象限。k<0,b>0时,函数图象经过第一、二、四象限。k<0,b<0时,函数图象经过第二、三、四象限。当k>0时,图象从左向右上升,y随x的增大而增大.当k<0时,图象从左向右下降,y随x的增大而减小.此环节采用101PPT随机点名功能。5.插入游戏,采取小组加分制,调节课堂气氛。学以致用、巩固练习1.函数 y=2x-5中,y随x的增大而_____,它的图象与y轴的交点坐标是_____.它的图象与x轴的交点坐标是____.2.已知点A(-5,a),B(4,b)在直线上y=-3x+2,则a b(填“>”“<”或“=”).此题利用几何画板进行演示。3.一次函数y=kx+b的图象如图所示,你能说出b的值吗?4.已知函数 y = kx的图象经过第二、四象限,那么函数y = kx-k的图象可能是( ) 此环节利用101PPT计时五分钟,计时结束小组先互判,后小组代表讲解有问题的题目,教师进行补充。四、导图总结、分层作业课堂小结分两部分,首先是知识小结,先由学困生先做答,再由学优生补充,使每个学生都能参与课堂。最后利用思维导图总结,思维导图使知识点更加系统、有条理,便于学生理解、记忆。其次是方法小结,学生通过回顾,归纳函数研究的方面,为以后其他函数的学习指明方向和方法。布置作业,我设计了个性化的选做作业,学生根据自己的能力进行选择。一方面是习题的练习,一方面学生继续探究一次函数的图象,从而巩固所学,并延伸所学。 考虑到让没有参与的学生也能认真思考,提出问题:请大家找出出现问题的地方,回答正确的同学会有相应的加分。四道典型例题,巩固一次函数的图象及性质。第一题考察一次函数的性质掌握情况,第二题渗透解题的多种方法,代数法以及图象的法,第三、四题渗透数形结合思想。练习遵循由易到难,由简到繁而设计。学生自己进行小结,发挥主体地位,学生互相补充。
板书设计 4.3.2一次函数的图象与性质
反思 教学反思 本课的内容比较抽象,学生不易理解。因此课前我让学生完成课前预习任务单,帮助学生初步感知,增强学生自主探究意识。课上利用几何画板,101PPT学科工具进行直观展示,解决学生疑惑。四个教学环节就是四个台阶,帮助学生一步步达成学习目标,并渗透数形结合的数学思想。几何画板,101PPT学科工具的利用解决了传统课堂不易演示,立体感受限的问题,培养了学生的数学思想和空间想象能力,真正做到了以学生为本的课堂。
小组合作 小组合作较好,能共同解决疑惑。
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
