人教版七年级下册数学第五章相交线与平行线证明推理填空题训练(含答案)
文档属性
| 名称 | 人教版七年级下册数学第五章相交线与平行线证明推理填空题训练(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 698.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-19 09:34:21 | ||
图片预览



文档简介
人教版七年级下册数学第五章相交线与平行线证明推理填空题训练
1.完成下面推理过程,并在括号内填上推理依据.
如图,.
求证:.
证明:,
_______(_______),
______(_______),
,
_______(等量代换),
________(________),
(________).
2.如图,,,.求证:.请补全证明过程,并在括号内填写相应的理论依据.
证明:∵(已知),
∴______( ).
∴______( ).
∵(已知),
∴(等量交换).
∴( ).
∴______( ).
∵(已知),
∴( ).
∴(等量交换).
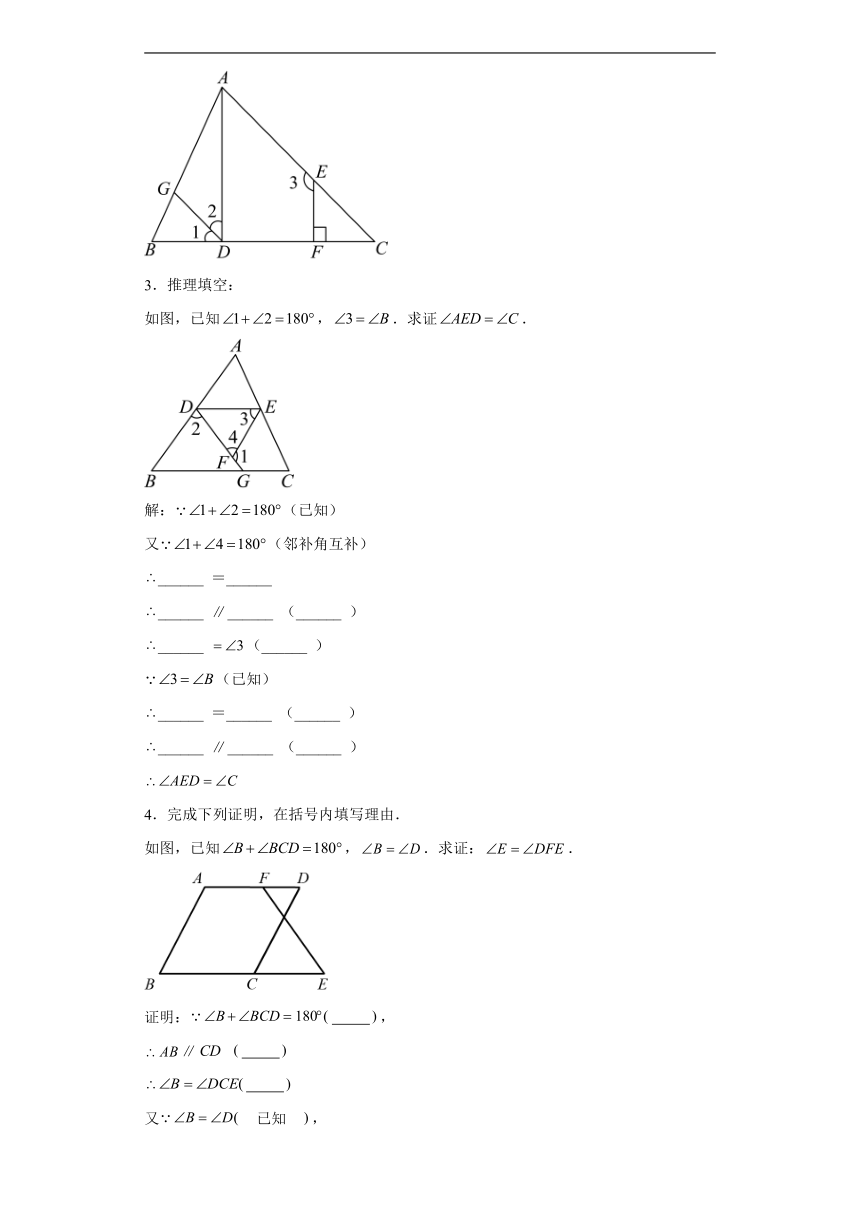
3.推理填空:
如图,已知,.求证.
解:(已知)
又(邻补角互补)
______ =______
______ ______ (______ )
______ (______ )
(已知)
______ =______ (______ )
______ ______ (______ )
4.完成下列证明,在括号内填写理由.
如图,已知,.求证:.
证明: ,
又 已知 ,
)
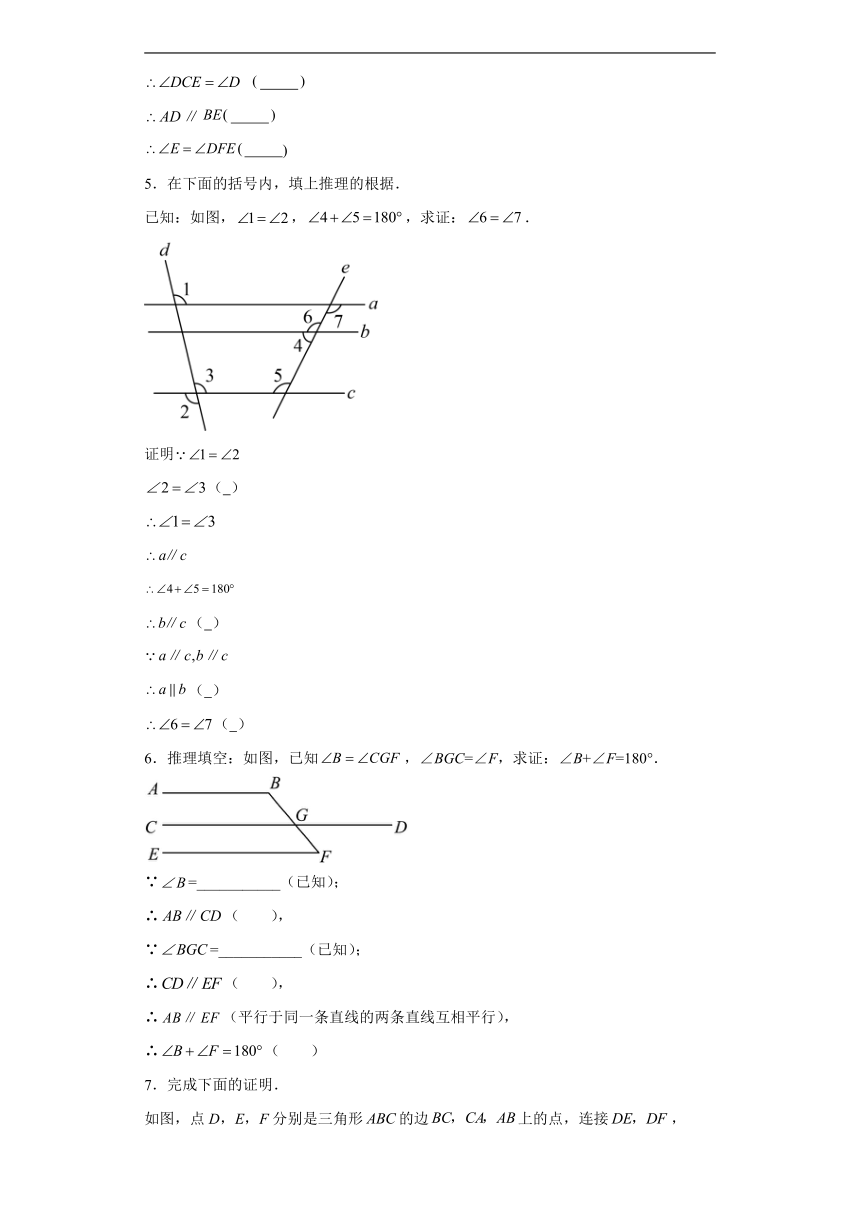
5.在下面的括号内,填上推理的根据.
已知:如图,,,求证:.
证明
( )
( )
( )
( )
6.推理填空:如图,已知,∠BGC=∠F,求证:∠B+∠F=180°.
∵=___________(已知);
∴( ),
∵=___________(已知);
∴( ),
∴(平行于同一条直线的两条直线互相平行),
∴( )
7.完成下面的证明.
如图,点D,E,F分别是三角形的边上的点,连接, ,,连接交于点G,求证.
证明:∵(已知),
∴______(______).
又∵(已知),
∴(______).
∴______(______).
∴(______).
8.如图,,平分,平分,求证:.完成下面的证明:
证明:∵,(已知),
∴,( )
∵(已知),
∴______( )
∵平分,平分(已知)
∴______,______( ).
∴(______+______)______.
∴.
9.完成下面的证明.
如图,已知,平分,与相交于点F,,试说明,把下面的说理过程补充完整.
证明:∵(已知)
∴(________________________)
∵平分(已知)
∴(________________________)
∴(________________________)
∵(已知)
∴______(________________________)
∴(________________________)
10.完成下面的证明.
已知:如图,,.
求证:.
证明:∵(已知),
∴______(__________).
∴______(__________).
∵(已知),(__________).
∴(等量代换).
∴(同位角相等,两直线平行),
∴(__________).
∴(等量代换).
11.完成下列证明:
如图,已知于点,于点,于点,,求证:.
证明:,(已知),
______(______),
______(两直线平行,内错角相等),
,(已知),
______(______),
( ),
∵( ),
.
12.如图,点E是三角形的边上一点,过点E作,连接,若,试说明:.请补充说明过程,并在括号内填上相应的理由.
证明:因为(已知),
所以__________(______________________),
所以__________(______________________).
因为(_____________),
所以_________(__________________),
所以_________(__________).
13.如图,平分,,,则也是的平分线,完成下列推理过程.
证明:是的平分线(已知),
( ).
(已知),
( ).
( ).
又(已知),
( ).
( ).
( ).
14.如图, 平分,点F在上,点E在上,与相交于点P,已知.求证:.
证明:(已知),
( ),
( ).
( )
_____( )
平分(已知),
_____( )
( ).
15.完成下面的证明.
如图,分别平分.求证.
证明:,
(____________________).
分别平分,
∴, ______(____________________).
又,
(____________________).
∴(____________________).
16.如图,已知,,试说明,下面是推理过程,请你填空.
证明:因为 (已知),
所以____________(____________),
所以______(两直线平行,内错角相等).
又因为(已知),
所以___________
即________.
所以_____________(内错角相等,两直线平行).
所以(____________).
17.已知,,、分别平分与,且.求证:.
请根据条件进行推理,得出结论,并在括号内注明理由.
证明:分别平分与,(已知)
,.(________).
,(________________)
,( )
,(已知)
,(等量代换)
________,(________________)
.(________________)
18.填写下列推理中的空格.
已知:如图,,,求证:.
证明:(已知),
______(____________),
又(____________),
______(____________),
(____________).
19.如图,,的平分线交于点F,交的延长线于点E,,求证:.
请将下面的证明过程及理由补充完整:
证明:∵(已知),
∴,(____________)
∵平分,
∴____________.(角平分线的定义)
∴.(____________)
∵(____________),
∴______.(____________)
∴.(____________)
∴.(____________)
20.完成下面的证明:
已知:如图,.求证:.
证明:(已知),
又∵______(平角定义),
∴(____________).
∴(____________).
∵(已证),
∴______(____________),
又∵(____________),
∴(____________).
参考答案:
1.;同旁内角互补,两直线平行;;两直线平行,同位角相等;;;内错角相等,两直线平行;两直线平行,内错角相等
2.;同位角相等,两平行线平行;;两直线平行,内错角相等;同旁内角互补,两直线平行;;两直线平行,同位角相等;垂直的定义
3.见解析
4.已知; 同旁内角互补,两直线平行;两直线平行,同位角相等;已知;等量代换;内错角相等,两直线平行;两直线平行,内错角相等
5.对顶角相等;同旁内角互补,两直线平行;如果两条直线都与第三条直线平行,那么这两条直线也互相平行;两直线平行,内错角相等
6.;同位角相等,两直线平行;;同位角相等,两直线平行;两直线平行,同旁内角互补
7.;两直线平行,同位角相等;等量代换;;同位角相等,两直线平行;两直线平行,同旁内角互补
8.见解析
9.两直线平行,内错角相等;角平分线的定义;等量代换;;等量代换;同位角相等,两直线平行
10.;内错角相等,两直线平行;;两直线平行,内错角相等;对顶角相等;两直线平行,同位角相等
11.;垂直同一条直线的两条直线相互平行;; ;等量代换;同位角相等,两直线平行;已知
12.见解析
13.角平分线的性质;两直线平行,内错角相等;,等量代换;, , 内错角相等,两直线平行;两直线平行,同位角相等 等量代换
14.邻补角定义;同角的补角相等;;内错角相等,两直线平行; ; 两直线平行,同位角相等;;角平分线定义;等量代换
15.见解析
16.、、同旁内角互补,两直线平行、、、、、、、两直线平行,内错角相等.
17.角平分线的定义;已知;等量代换;;内错角相等,两直线平行;两直线平行,同旁内角互补
18.;两直线平行,内错角相等;已知;;等量代换;同位角相等,两直线平行
19.两直线平行,内错角相等;;等量代换;已知;;同旁内角互补,两直线平行;两直线平行,同位角相等;等量代换.
20.,同角的补角相等,内错角相等两直线平行,,两直线平行同位角相等,对顶角相等,等量代换
答案第2页,共2页
答案第1页,共2页
1.完成下面推理过程,并在括号内填上推理依据.
如图,.
求证:.
证明:,
_______(_______),
______(_______),
,
_______(等量代换),
________(________),
(________).
2.如图,,,.求证:.请补全证明过程,并在括号内填写相应的理论依据.
证明:∵(已知),
∴______( ).
∴______( ).
∵(已知),
∴(等量交换).
∴( ).
∴______( ).
∵(已知),
∴( ).
∴(等量交换).
3.推理填空:
如图,已知,.求证.
解:(已知)
又(邻补角互补)
______ =______
______ ______ (______ )
______ (______ )
(已知)
______ =______ (______ )
______ ______ (______ )
4.完成下列证明,在括号内填写理由.
如图,已知,.求证:.
证明: ,
又 已知 ,
)
5.在下面的括号内,填上推理的根据.
已知:如图,,,求证:.
证明
( )
( )
( )
( )
6.推理填空:如图,已知,∠BGC=∠F,求证:∠B+∠F=180°.
∵=___________(已知);
∴( ),
∵=___________(已知);
∴( ),
∴(平行于同一条直线的两条直线互相平行),
∴( )
7.完成下面的证明.
如图,点D,E,F分别是三角形的边上的点,连接, ,,连接交于点G,求证.
证明:∵(已知),
∴______(______).
又∵(已知),
∴(______).
∴______(______).
∴(______).
8.如图,,平分,平分,求证:.完成下面的证明:
证明:∵,(已知),
∴,( )
∵(已知),
∴______( )
∵平分,平分(已知)
∴______,______( ).
∴(______+______)______.
∴.
9.完成下面的证明.
如图,已知,平分,与相交于点F,,试说明,把下面的说理过程补充完整.
证明:∵(已知)
∴(________________________)
∵平分(已知)
∴(________________________)
∴(________________________)
∵(已知)
∴______(________________________)
∴(________________________)
10.完成下面的证明.
已知:如图,,.
求证:.
证明:∵(已知),
∴______(__________).
∴______(__________).
∵(已知),(__________).
∴(等量代换).
∴(同位角相等,两直线平行),
∴(__________).
∴(等量代换).
11.完成下列证明:
如图,已知于点,于点,于点,,求证:.
证明:,(已知),
______(______),
______(两直线平行,内错角相等),
,(已知),
______(______),
( ),
∵( ),
.
12.如图,点E是三角形的边上一点,过点E作,连接,若,试说明:.请补充说明过程,并在括号内填上相应的理由.
证明:因为(已知),
所以__________(______________________),
所以__________(______________________).
因为(_____________),
所以_________(__________________),
所以_________(__________).
13.如图,平分,,,则也是的平分线,完成下列推理过程.
证明:是的平分线(已知),
( ).
(已知),
( ).
( ).
又(已知),
( ).
( ).
( ).
14.如图, 平分,点F在上,点E在上,与相交于点P,已知.求证:.
证明:(已知),
( ),
( ).
( )
_____( )
平分(已知),
_____( )
( ).
15.完成下面的证明.
如图,分别平分.求证.
证明:,
(____________________).
分别平分,
∴, ______(____________________).
又,
(____________________).
∴(____________________).
16.如图,已知,,试说明,下面是推理过程,请你填空.
证明:因为 (已知),
所以____________(____________),
所以______(两直线平行,内错角相等).
又因为(已知),
所以___________
即________.
所以_____________(内错角相等,两直线平行).
所以(____________).
17.已知,,、分别平分与,且.求证:.
请根据条件进行推理,得出结论,并在括号内注明理由.
证明:分别平分与,(已知)
,.(________).
,(________________)
,( )
,(已知)
,(等量代换)
________,(________________)
.(________________)
18.填写下列推理中的空格.
已知:如图,,,求证:.
证明:(已知),
______(____________),
又(____________),
______(____________),
(____________).
19.如图,,的平分线交于点F,交的延长线于点E,,求证:.
请将下面的证明过程及理由补充完整:
证明:∵(已知),
∴,(____________)
∵平分,
∴____________.(角平分线的定义)
∴.(____________)
∵(____________),
∴______.(____________)
∴.(____________)
∴.(____________)
20.完成下面的证明:
已知:如图,.求证:.
证明:(已知),
又∵______(平角定义),
∴(____________).
∴(____________).
∵(已证),
∴______(____________),
又∵(____________),
∴(____________).
参考答案:
1.;同旁内角互补,两直线平行;;两直线平行,同位角相等;;;内错角相等,两直线平行;两直线平行,内错角相等
2.;同位角相等,两平行线平行;;两直线平行,内错角相等;同旁内角互补,两直线平行;;两直线平行,同位角相等;垂直的定义
3.见解析
4.已知; 同旁内角互补,两直线平行;两直线平行,同位角相等;已知;等量代换;内错角相等,两直线平行;两直线平行,内错角相等
5.对顶角相等;同旁内角互补,两直线平行;如果两条直线都与第三条直线平行,那么这两条直线也互相平行;两直线平行,内错角相等
6.;同位角相等,两直线平行;;同位角相等,两直线平行;两直线平行,同旁内角互补
7.;两直线平行,同位角相等;等量代换;;同位角相等,两直线平行;两直线平行,同旁内角互补
8.见解析
9.两直线平行,内错角相等;角平分线的定义;等量代换;;等量代换;同位角相等,两直线平行
10.;内错角相等,两直线平行;;两直线平行,内错角相等;对顶角相等;两直线平行,同位角相等
11.;垂直同一条直线的两条直线相互平行;; ;等量代换;同位角相等,两直线平行;已知
12.见解析
13.角平分线的性质;两直线平行,内错角相等;,等量代换;, , 内错角相等,两直线平行;两直线平行,同位角相等 等量代换
14.邻补角定义;同角的补角相等;;内错角相等,两直线平行; ; 两直线平行,同位角相等;;角平分线定义;等量代换
15.见解析
16.、、同旁内角互补,两直线平行、、、、、、、两直线平行,内错角相等.
17.角平分线的定义;已知;等量代换;;内错角相等,两直线平行;两直线平行,同旁内角互补
18.;两直线平行,内错角相等;已知;;等量代换;同位角相等,两直线平行
19.两直线平行,内错角相等;;等量代换;已知;;同旁内角互补,两直线平行;两直线平行,同位角相等;等量代换.
20.,同角的补角相等,内错角相等两直线平行,,两直线平行同位角相等,对顶角相等,等量代换
答案第2页,共2页
答案第1页,共2页
