人教版七年级下册 第6章 实数 单元测试卷 含解析
文档属性
| 名称 | 人教版七年级下册 第6章 实数 单元测试卷 含解析 |

|
|
| 格式 | doc | ||
| 文件大小 | 381.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-18 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
人教版七年级下册 第6章 实数 单元测试卷
一.选择题(共10小题,满分30分,每小题3分)
1.2023的算术平方根是( )
A.2023 B.﹣ C.± D.
2.9的平方根是( )
A.3 B.﹣3 C.±3 D.
3.平方根等于它本身的数是( )
A.0 B.1 C.2 D.4
4.在实数﹣,4.212121……,,﹣ 中,无理数有( )
A.1个 B.2个 C.3个 D.4个
5.若=3.5﹣x,则x的值不能是( )
A.4 B.3 C.2 D.1
6.下列运算一定正确的是( )
A.=±7 B.(﹣)2=7 C.﹣=7 D.=7
7.已知8.622=74.3044,若x2=0.743044,则x的值( )
A.86.2 B.0.862 C.±0.862 D.±86.2
8.一个正方体的棱长为a,体积为b,则下列说法正确的是( )
A.b的立方根±a B.a是b的立方根
C. D.
9.a,b是两个连续整数,若,则ab是( )
A.12 B.13 C.20 D.21
10.设S1=1,S2=1,S3=1,…,Sn=1,则的值为( )
A. B. C. D.
二.填空题(共6小题,满分24分,每小题4分)
11.的算术平方根是 .
12.比较大小: 5(填“>”“<”或“=”).
13.的立方根是 .
14.实数﹣1的相反数是 .
15.若一个正数的平方根为2a+1和2﹣a,则a的值是 .
16.定义一种运算:对于任意实数a,b,都有a*b=(a﹣1)2﹣b2,则= .
三.解答题(共5小题,满分46分)
17.(10分)计算下列各题
(1)﹣﹣+|1﹣|
(2)﹣+.
18.(10分)求下列各式中的x
(1)25x2﹣36=0;
(2)(x+3)3=27.
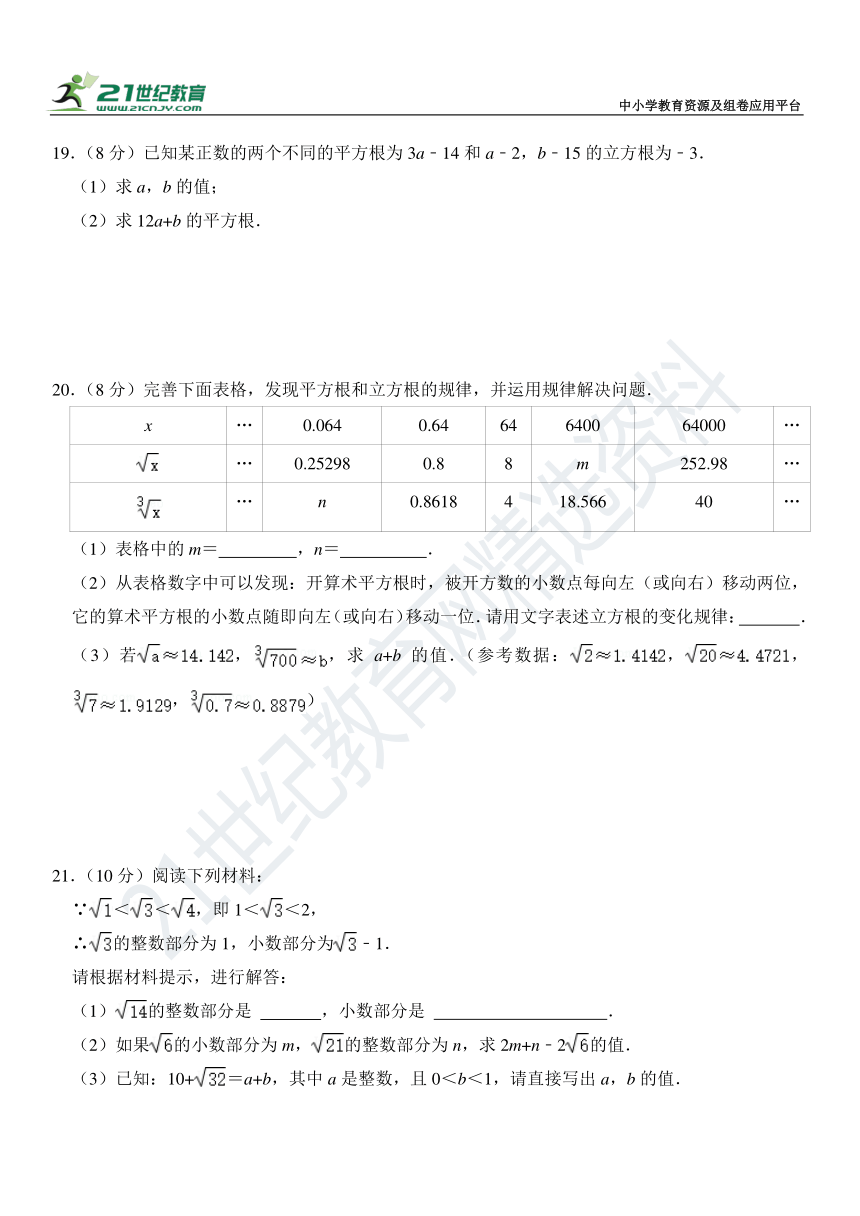
19.(8分)已知某正数的两个不同的平方根为3a﹣14和a﹣2,b﹣15的立方根为﹣3.
(1)求a,b的值;
(2)求12a+b的平方根.
20.(8分)完善下面表格,发现平方根和立方根的规律,并运用规律解决问题.
x … 0.064 0.64 64 6400 64000 …
… 0.25298 0.8 8 m 252.98 …
… n 0.8618 4 18.566 40 …
(1)表格中的m= ,n= .
(2)从表格数字中可以发现:开算术平方根时,被开方数的小数点每向左(或向右)移动两位,它的算术平方根的小数点随即向左(或向右)移动一位.请用文字表述立方根的变化规律: .
(3)若,,求a+b的值.(参考数据:,,,)
21.(10分)阅读下列材料:
∵<<,即1<<2,
∴的整数部分为1,小数部分为﹣1.
请根据材料提示,进行解答:
(1)的整数部分是 ,小数部分是 .
(2)如果的小数部分为m,的整数部分为n,求2m+n﹣2的值.
(3)已知:10+=a+b,其中a是整数,且0<b<1,请直接写出a,b的值.
人教版七年级下册 第6章 实数 单元测试卷
答案与解析
一.选择题(共10小题,满分30分,每小题3分)
1.2023的算术平方根是( )
A.2023 B.﹣ C.± D.
【分析】根据算术平方根的定义进行解答即可.
【解答】解:2023的算术平方根是,
故选:D.
2.9的平方根是( )
A.3 B.﹣3 C.±3 D.
【分析】根据平方根的含义和求法,可得9的平方根是:±=±3,据此解答即可.
【解答】解:9的平方根是±=±3.
故选:C.
3.平方根等于它本身的数是( )
A.0 B.1 C.2 D.4
【分析】根据平方根的定义即可求得答案.
【解答】解:平方根等于它本身的数是0,
故选:A.
4.在实数﹣,4.212121……,,﹣ 中,无理数有( )
A.1个 B.2个 C.3个 D.4个
【分析】根据无理数的定义解答即可.
【解答】解:﹣,是无理数,共2个.
故选:B.
5.若=3.5﹣x,则x的值不能是( )
A.4 B.3 C.2 D.1
【分析】根据算术平方根是非负数得出3.5﹣x≥0,即可求出x的取值范围,从而进行判断.
【解答】解:若=3.5﹣x,
则3.5﹣x≥0,
解得x≤3.5,
∴x的值不能是4,
故选:A.
6.下列运算一定正确的是( )
A.=±7 B.(﹣)2=7 C.﹣=7 D.=7
【分析】根据平方根、立方根的定义判断即可.
【解答】解:A.=7,此选项错误,不符合题意;
B.(﹣)2=7,此选项正确,符合题意;
C.﹣=﹣7,此选项错误,不符合题意;
D.=﹣7,此选项错误,不符合题意;
故选:B.
7.已知8.622=74.3044,若x2=0.743044,则x的值( )
A.86.2 B.0.862 C.±0.862 D.±86.2
【分析】根据两式结果相差2位小数点,利用乘方的意义即可求出x的值.
【解答】解:∵8.622=74.3044,x2=0.743044,
∴x2=0.8622,
则x=±0.862.
故选:C.
8.一个正方体的棱长为a,体积为b,则下列说法正确的是( )
A.b的立方根±a B.a是b的立方根
C. D.
【分析】根据正方体的体积计算公式以及立方根的定义进行判断即可.
【解答】解:由正方体的体积公式可得,a3=b,即a是b的立方根,
故选:B.
9.a,b是两个连续整数,若,则ab是( )
A.12 B.13 C.20 D.21
【分析】根据算术平方根的定义估算无理数的大小,确定a、b的值,再代入计算即可.
【解答】解:∵<<,即4<<5,
∴a=4,b=5,
∴ab=20.
故选:C.
10.设S1=1,S2=1,S3=1,…,Sn=1,则的值为( )
A. B. C. D.
【分析】观察第一步的几个计算结果,得出一般规律.
【解答】解:,,,=,…,
,
∴
=1+1…+1+﹣
=24+1﹣
=.
故选:A.
二.填空题(共6小题,满分24分,每小题4分)
11.的算术平方根是 3 .
【分析】如果一个正数x的平方等于a,即x2=a,那么这个正数x叫做a的算术平方根.记为,由此即可得到答案.
【解答】解:∵=9,
∴的算术平方根是3.
故答案为:3.
12.比较大小: > 5(填“>”“<”或“=”).
【分析】先把5化成,再与进行比较,即可得出答案.
【解答】解:∵5=,
∴>,
∴>5;
故答案为:>.
13.的立方根是 .
【分析】根据立方根的定义进行求解.
【解答】解:∵,
∴的立方根是.
故答案为:.
14.实数﹣1的相反数是 1﹣ .
【分析】根据只有符号不同的两个数互为相反数,可得答案.
【解答】解:﹣1的相反数是1﹣,
故答案为:1﹣.
15.若一个正数的平方根为2a+1和2﹣a,则a的值是 ﹣3 .
【分析】根据正数有两个平方根,且它们互为相反数和互为相反数的两个数的和为0,即可得到关于a的方程.
【解答】解:根据题意,得
2a+1+(2﹣a)=0,
解得a=﹣3.
故答案为:﹣3.
16.定义一种运算:对于任意实数a,b,都有a*b=(a﹣1)2﹣b2,则= ﹣1 .
【分析】根据题意列式计算即可.
【解答】解:原式=(+1﹣1)2﹣(﹣)2
=5﹣6
=﹣1,
故答案为:﹣1.
三.解答题(共5小题,满分46分)
17.(10分)计算下列各题
(1)﹣﹣+|1﹣|
(2)﹣+.
【分析】(1)原式利用平方根、立方根定义,以及绝对值的代数意义化简,计算即可得到结果;
(2)原式利用平方根、立方根的定义计算即可得到结果.
【解答】解:(1)原式=2﹣2﹣3+﹣1=﹣4;
(2)原式=5+3+=8.
18.(10分)求下列各式中的x
(1)25x2﹣36=0;
(2)(x+3)3=27.
【分析】(1)移项,系数化成1,再根据平方根的定义求出即可;
(2)系数化成1,再根据立方根定义求出即可.
【解答】解:(1)25x2﹣36=0,
25x2=36,
x2=,
x=±;
(2)(x+3)3=27,
x+3=3,
x=0.
19.(8分)已知某正数的两个不同的平方根为3a﹣14和a﹣2,b﹣15的立方根为﹣3.
(1)求a,b的值;
(2)求12a+b的平方根.
【分析】(1)根据正数的两个不同的平方根是3a﹣14和a﹣2,列出方程解出a,再根据b﹣15的立方根为﹣3,列出方程解出b;
(2)把a=4、b=﹣12代入12a+b计算出代数式的值,然后求它的平方根.
【解答】解:(1)∵正数的两个不同的平方根是3a﹣14和a﹣2,
∴3a﹣14+a﹣2=0,
解得a=4,
∵b﹣15的立方根为﹣3,
∴b﹣15=﹣27,
解得b=﹣12,
∴a=4、b=﹣12;
(2)a=4、b=﹣12代入12a+b
得12×4+(﹣12)=36,
∴4a+b的平方根是±6.
20.(8分)完善下面表格,发现平方根和立方根的规律,并运用规律解决问题.
x … 0.064 0.64 64 6400 64000 …
… 0.25298 0.8 8 m 252.98 …
… n 0.8618 4 18.566 40 …
(1)表格中的m= 80 ,n= 0.4 .
(2)从表格数字中可以发现:开算术平方根时,被开方数的小数点每向左(或向右)移动两位,它的算术平方根的小数点随即向左(或向右)移动一位.请用文字表述立方根的变化规律: 开立方根时,被开方数的小数点每向左(或向右)移动三位,它的立方根的小数点随即向左(或向右)移动一位 .
(3)若,,求a+b的值.(参考数据:,,,)
【分析】(1)根据平方根、立方根的定义进行计算即可;
(2)由表格中的数字变化规律得出结论;
(3)根据算术平方根、立方根的变化规律进行解答即可.
【解答】解:(1)∵802=6400,
∴6400的算术平方根是=80,
即m=80,
∵0.43=0.064,
∴0.064的立方根是=0.4,
即n=0.4,
故答案为:80,0.4;
(2)故答案为:开立方根时,被开方数的小数点每向左(或向右)移动三位,它的立方根的小数点随即向左(或向右)移动一位;
(3)根据平方根的变化规律得:
∵≈1.4142,
∴≈14.142,
即a=200,
根据立方根的变化规律得:
∵≈0.8879,
∴≈8.879,
即b=8.879,
∴a+b=200+8.879
=208.879.
21.(10分)阅读下列材料:
∵<<,即1<<2,
∴的整数部分为1,小数部分为﹣1.
请根据材料提示,进行解答:
(1)的整数部分是 3 ,小数部分是 ﹣3 .
(2)如果的小数部分为m,的整数部分为n,求2m+n﹣2的值.
(3)已知:10+=a+b,其中a是整数,且0<b<1,请直接写出a,b的值.
【分析】(1)估算的大小即可;
(2)估算无理数和的大小,进而确定m,n的值,再代入计算即可;
(3)估算无理数的大小,进而确定10+的大小,确定a,b的值即可.
【解答】解:(1)∵<<,即3<<4,
∴的整数部分是3,小数部分是﹣3,
故答案为:3,﹣3;
(2)∵2<<3,4<<5,
∴m=﹣2,n=4,
∴2m+n﹣2
=2(﹣2)+4﹣2
=2﹣4+4﹣2
=0;
(3)∵5<<6,
∴15<10+<16,
∴10+的整数部分是15,小数部分是10+﹣15=﹣5,
∵10+=a+b,其中a是整数,且0<b<1,
∴a=15,b=﹣5.
人教版七年级下册 第6章 实数 单元测试卷
一.选择题(共10小题,满分30分,每小题3分)
1.2023的算术平方根是( )
A.2023 B.﹣ C.± D.
2.9的平方根是( )
A.3 B.﹣3 C.±3 D.
3.平方根等于它本身的数是( )
A.0 B.1 C.2 D.4
4.在实数﹣,4.212121……,,﹣ 中,无理数有( )
A.1个 B.2个 C.3个 D.4个
5.若=3.5﹣x,则x的值不能是( )
A.4 B.3 C.2 D.1
6.下列运算一定正确的是( )
A.=±7 B.(﹣)2=7 C.﹣=7 D.=7
7.已知8.622=74.3044,若x2=0.743044,则x的值( )
A.86.2 B.0.862 C.±0.862 D.±86.2
8.一个正方体的棱长为a,体积为b,则下列说法正确的是( )
A.b的立方根±a B.a是b的立方根
C. D.
9.a,b是两个连续整数,若,则ab是( )
A.12 B.13 C.20 D.21
10.设S1=1,S2=1,S3=1,…,Sn=1,则的值为( )
A. B. C. D.
二.填空题(共6小题,满分24分,每小题4分)
11.的算术平方根是 .
12.比较大小: 5(填“>”“<”或“=”).
13.的立方根是 .
14.实数﹣1的相反数是 .
15.若一个正数的平方根为2a+1和2﹣a,则a的值是 .
16.定义一种运算:对于任意实数a,b,都有a*b=(a﹣1)2﹣b2,则= .
三.解答题(共5小题,满分46分)
17.(10分)计算下列各题
(1)﹣﹣+|1﹣|
(2)﹣+.
18.(10分)求下列各式中的x
(1)25x2﹣36=0;
(2)(x+3)3=27.
19.(8分)已知某正数的两个不同的平方根为3a﹣14和a﹣2,b﹣15的立方根为﹣3.
(1)求a,b的值;
(2)求12a+b的平方根.
20.(8分)完善下面表格,发现平方根和立方根的规律,并运用规律解决问题.
x … 0.064 0.64 64 6400 64000 …
… 0.25298 0.8 8 m 252.98 …
… n 0.8618 4 18.566 40 …
(1)表格中的m= ,n= .
(2)从表格数字中可以发现:开算术平方根时,被开方数的小数点每向左(或向右)移动两位,它的算术平方根的小数点随即向左(或向右)移动一位.请用文字表述立方根的变化规律: .
(3)若,,求a+b的值.(参考数据:,,,)
21.(10分)阅读下列材料:
∵<<,即1<<2,
∴的整数部分为1,小数部分为﹣1.
请根据材料提示,进行解答:
(1)的整数部分是 ,小数部分是 .
(2)如果的小数部分为m,的整数部分为n,求2m+n﹣2的值.
(3)已知:10+=a+b,其中a是整数,且0<b<1,请直接写出a,b的值.
人教版七年级下册 第6章 实数 单元测试卷
答案与解析
一.选择题(共10小题,满分30分,每小题3分)
1.2023的算术平方根是( )
A.2023 B.﹣ C.± D.
【分析】根据算术平方根的定义进行解答即可.
【解答】解:2023的算术平方根是,
故选:D.
2.9的平方根是( )
A.3 B.﹣3 C.±3 D.
【分析】根据平方根的含义和求法,可得9的平方根是:±=±3,据此解答即可.
【解答】解:9的平方根是±=±3.
故选:C.
3.平方根等于它本身的数是( )
A.0 B.1 C.2 D.4
【分析】根据平方根的定义即可求得答案.
【解答】解:平方根等于它本身的数是0,
故选:A.
4.在实数﹣,4.212121……,,﹣ 中,无理数有( )
A.1个 B.2个 C.3个 D.4个
【分析】根据无理数的定义解答即可.
【解答】解:﹣,是无理数,共2个.
故选:B.
5.若=3.5﹣x,则x的值不能是( )
A.4 B.3 C.2 D.1
【分析】根据算术平方根是非负数得出3.5﹣x≥0,即可求出x的取值范围,从而进行判断.
【解答】解:若=3.5﹣x,
则3.5﹣x≥0,
解得x≤3.5,
∴x的值不能是4,
故选:A.
6.下列运算一定正确的是( )
A.=±7 B.(﹣)2=7 C.﹣=7 D.=7
【分析】根据平方根、立方根的定义判断即可.
【解答】解:A.=7,此选项错误,不符合题意;
B.(﹣)2=7,此选项正确,符合题意;
C.﹣=﹣7,此选项错误,不符合题意;
D.=﹣7,此选项错误,不符合题意;
故选:B.
7.已知8.622=74.3044,若x2=0.743044,则x的值( )
A.86.2 B.0.862 C.±0.862 D.±86.2
【分析】根据两式结果相差2位小数点,利用乘方的意义即可求出x的值.
【解答】解:∵8.622=74.3044,x2=0.743044,
∴x2=0.8622,
则x=±0.862.
故选:C.
8.一个正方体的棱长为a,体积为b,则下列说法正确的是( )
A.b的立方根±a B.a是b的立方根
C. D.
【分析】根据正方体的体积计算公式以及立方根的定义进行判断即可.
【解答】解:由正方体的体积公式可得,a3=b,即a是b的立方根,
故选:B.
9.a,b是两个连续整数,若,则ab是( )
A.12 B.13 C.20 D.21
【分析】根据算术平方根的定义估算无理数的大小,确定a、b的值,再代入计算即可.
【解答】解:∵<<,即4<<5,
∴a=4,b=5,
∴ab=20.
故选:C.
10.设S1=1,S2=1,S3=1,…,Sn=1,则的值为( )
A. B. C. D.
【分析】观察第一步的几个计算结果,得出一般规律.
【解答】解:,,,=,…,
,
∴
=1+1…+1+﹣
=24+1﹣
=.
故选:A.
二.填空题(共6小题,满分24分,每小题4分)
11.的算术平方根是 3 .
【分析】如果一个正数x的平方等于a,即x2=a,那么这个正数x叫做a的算术平方根.记为,由此即可得到答案.
【解答】解:∵=9,
∴的算术平方根是3.
故答案为:3.
12.比较大小: > 5(填“>”“<”或“=”).
【分析】先把5化成,再与进行比较,即可得出答案.
【解答】解:∵5=,
∴>,
∴>5;
故答案为:>.
13.的立方根是 .
【分析】根据立方根的定义进行求解.
【解答】解:∵,
∴的立方根是.
故答案为:.
14.实数﹣1的相反数是 1﹣ .
【分析】根据只有符号不同的两个数互为相反数,可得答案.
【解答】解:﹣1的相反数是1﹣,
故答案为:1﹣.
15.若一个正数的平方根为2a+1和2﹣a,则a的值是 ﹣3 .
【分析】根据正数有两个平方根,且它们互为相反数和互为相反数的两个数的和为0,即可得到关于a的方程.
【解答】解:根据题意,得
2a+1+(2﹣a)=0,
解得a=﹣3.
故答案为:﹣3.
16.定义一种运算:对于任意实数a,b,都有a*b=(a﹣1)2﹣b2,则= ﹣1 .
【分析】根据题意列式计算即可.
【解答】解:原式=(+1﹣1)2﹣(﹣)2
=5﹣6
=﹣1,
故答案为:﹣1.
三.解答题(共5小题,满分46分)
17.(10分)计算下列各题
(1)﹣﹣+|1﹣|
(2)﹣+.
【分析】(1)原式利用平方根、立方根定义,以及绝对值的代数意义化简,计算即可得到结果;
(2)原式利用平方根、立方根的定义计算即可得到结果.
【解答】解:(1)原式=2﹣2﹣3+﹣1=﹣4;
(2)原式=5+3+=8.
18.(10分)求下列各式中的x
(1)25x2﹣36=0;
(2)(x+3)3=27.
【分析】(1)移项,系数化成1,再根据平方根的定义求出即可;
(2)系数化成1,再根据立方根定义求出即可.
【解答】解:(1)25x2﹣36=0,
25x2=36,
x2=,
x=±;
(2)(x+3)3=27,
x+3=3,
x=0.
19.(8分)已知某正数的两个不同的平方根为3a﹣14和a﹣2,b﹣15的立方根为﹣3.
(1)求a,b的值;
(2)求12a+b的平方根.
【分析】(1)根据正数的两个不同的平方根是3a﹣14和a﹣2,列出方程解出a,再根据b﹣15的立方根为﹣3,列出方程解出b;
(2)把a=4、b=﹣12代入12a+b计算出代数式的值,然后求它的平方根.
【解答】解:(1)∵正数的两个不同的平方根是3a﹣14和a﹣2,
∴3a﹣14+a﹣2=0,
解得a=4,
∵b﹣15的立方根为﹣3,
∴b﹣15=﹣27,
解得b=﹣12,
∴a=4、b=﹣12;
(2)a=4、b=﹣12代入12a+b
得12×4+(﹣12)=36,
∴4a+b的平方根是±6.
20.(8分)完善下面表格,发现平方根和立方根的规律,并运用规律解决问题.
x … 0.064 0.64 64 6400 64000 …
… 0.25298 0.8 8 m 252.98 …
… n 0.8618 4 18.566 40 …
(1)表格中的m= 80 ,n= 0.4 .
(2)从表格数字中可以发现:开算术平方根时,被开方数的小数点每向左(或向右)移动两位,它的算术平方根的小数点随即向左(或向右)移动一位.请用文字表述立方根的变化规律: 开立方根时,被开方数的小数点每向左(或向右)移动三位,它的立方根的小数点随即向左(或向右)移动一位 .
(3)若,,求a+b的值.(参考数据:,,,)
【分析】(1)根据平方根、立方根的定义进行计算即可;
(2)由表格中的数字变化规律得出结论;
(3)根据算术平方根、立方根的变化规律进行解答即可.
【解答】解:(1)∵802=6400,
∴6400的算术平方根是=80,
即m=80,
∵0.43=0.064,
∴0.064的立方根是=0.4,
即n=0.4,
故答案为:80,0.4;
(2)故答案为:开立方根时,被开方数的小数点每向左(或向右)移动三位,它的立方根的小数点随即向左(或向右)移动一位;
(3)根据平方根的变化规律得:
∵≈1.4142,
∴≈14.142,
即a=200,
根据立方根的变化规律得:
∵≈0.8879,
∴≈8.879,
即b=8.879,
∴a+b=200+8.879
=208.879.
21.(10分)阅读下列材料:
∵<<,即1<<2,
∴的整数部分为1,小数部分为﹣1.
请根据材料提示,进行解答:
(1)的整数部分是 3 ,小数部分是 ﹣3 .
(2)如果的小数部分为m,的整数部分为n,求2m+n﹣2的值.
(3)已知:10+=a+b,其中a是整数,且0<b<1,请直接写出a,b的值.
【分析】(1)估算的大小即可;
(2)估算无理数和的大小,进而确定m,n的值,再代入计算即可;
(3)估算无理数的大小,进而确定10+的大小,确定a,b的值即可.
【解答】解:(1)∵<<,即3<<4,
∴的整数部分是3,小数部分是﹣3,
故答案为:3,﹣3;
(2)∵2<<3,4<<5,
∴m=﹣2,n=4,
∴2m+n﹣2
=2(﹣2)+4﹣2
=2﹣4+4﹣2
=0;
(3)∵5<<6,
∴15<10+<16,
∴10+的整数部分是15,小数部分是10+﹣15=﹣5,
∵10+=a+b,其中a是整数,且0<b<1,
∴a=15,b=﹣5.
