28.2.2应用举例 课件(共30张PPT)初中数学人教版九年级下册
文档属性
| 名称 | 28.2.2应用举例 课件(共30张PPT)初中数学人教版九年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-19 11:51:19 | ||
图片预览











文档简介
(共30张PPT)
28.2.2 应用举例
——第二十八章锐角三角函数
教学目标
01.了解俯角、仰角、方位角、坡度、坡角等相关概念 重点
02.能够把实际问题转化为数学问题,建立数学模型,并运用解直角三角形求解 重难点
上节课我们学习了解直角三角形,在Rt△ABC中除直角外的五个元素之间有什么联系?
(2)两锐角之间的关系:
∠A+∠B=90°
(1)三边之间的关系:
(勾股定理)
(3)边角之间的关系:
上节课我们还对除直角外的五个元素中知道几个元素可以解直角三角形进行了讨论
在直角三角形中,除直角外的五个元素中,已知其中的两个元素(至少有一个是边),可求出其余的未知元素(知二求三)
下面我们开始本节课的学习,解直角三角形在实际问题中的应用
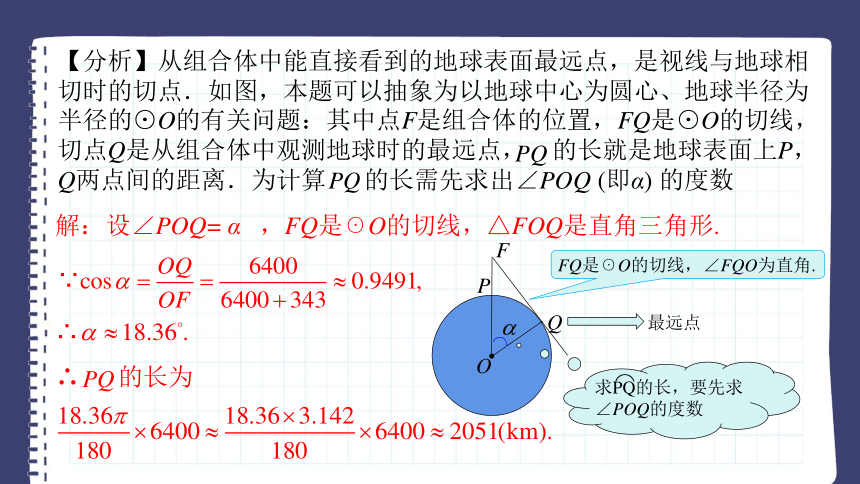
2012年6月18日,“神州”九号载人航天飞船与“天宫”一号目标飞行器成功实现交会对接. “神州”九号与“天宫”一号的组合体在离地球表面343km的圆形轨道上运行. 如图,当组合体运行到离地球表面P点的正上方时,从中能直接看到的地球表面最远的点在什么位置?最远点与P点的距离是多少(地球半径约为6400 km,π取3.142,结果取整数)?
探究一
【问题1】这个实际问题可以抽象成数学图形吗?
可以抽象为以地球中心为圆心、地球半径为半径的⊙O的有关问题.
【问题2】当组合体运行到地球表面P点的正上方时,从中能直接看到的地球表面最远的点在什么位置?
最远点是视线与地球相切时的切点,即点Q.
【问题3】在图中,最远点与P点的距离可以用什么表示?
【分析】从组合体中能直接看到的地球表面最远点,是视线与地球相切时的切点.如图,本题可以抽象为以地球中心为圆心、地球半径为半径的⊙O的有关问题:其中点F是组合体的位置,FQ是⊙O的切线,切点Q是从组合体中观测地球时的最远点, 的长就是地球表面上P,Q两点间的距离.为计算 的长需先求出∠POQ (即α) 的度数
O
F
P
Q
FQ是☉O的切线,∠FQO为直角.
最远点
求PQ的长,要先求∠POQ的度数
⌒
解:设∠POQ= α ,FQ是☉O的切线,△FOQ是直角三角形.
∴ 的长为
热气球的探测器显示,从热气球看一栋楼顶部的仰角为30°,看这栋楼底部的俯角为60°,热气球与楼的水平距离为120 m,这栋楼有多高(结果取整数)?
探究二
【提问】什么是俯角、仰角?
眼睛
水平线
视线
视线
仰角
俯角
仰角:在视线与水平线所成的角中,视线在水平线上方的是仰角.
俯角:在视线与水平线所成的角中,视线在水平线下方的是俯角
热气球的探测器显示,从热气球看一栋楼顶部的仰角为30°,看这栋楼底部的俯角为60°,热气球与楼的水平距离为120 m,这栋楼有多高(结果取整数)?
探究二
【分析】在图中,α=30°,β=60°.
在Rt△ABD中,α =30°,AD=120,所以利用解直角三角形的知识求出BD;类似地可以求出CD,进而求出BC.
探究二
解:如图,a = 30°,β= 60°, AD=120.
答:这栋楼高约为277.1m.
【归纳】解决与仰角、俯角有关的实际问题的方法:
根据仰角、俯角的定义画出水平线、视线,找准仰角、俯角,结合题意,从实际问题情境中抽象出含仰角或俯角的直角三角形,然后利用解直角三角形的方法进行解答.
探究三
如图,一艘海轮位于灯塔P的北偏东65°方向,距离灯塔80 n mile的A 处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东34°方向上的B 处.这时,B处距离灯塔 P有多远(结果取整数)?
65°
34°
P
B
C
A
【提问】同学们对方向角有什么了解?
方向角:指北或指南的方向线与目标线所成的小于90°的角叫做方向角.如图所示
30°
45°
B
O
A
东
西
北
南
45°
45°
西南
O
东北
东
西
北
南
西北
东南
探究三
65°
34°
P
B
C
A
解:如图 ,在Rt△APC中,
PC=PA·cos(90°-65°)
=80×cos25°
≈ 72.505.
在Rt△BPC中,∠B=34°,
因此,当海轮到达位于灯塔P的南偏东34°方向
时,它距离灯塔P大约130n mile.
如图,某水库大坝的横截面为梯形ABCD,AF=DE=6m.斜面坡度i=1:1.5是 指坡面的铅直高度AF与水平宽度BF的比,斜面坡度i=l:3是指DE与CE
的比.根据图中数据,求:
(1)坡角α和β的度数;
(2)斜坡AB的长(结果保留小数点后一位).
探究四
α
l
h
i= h : l
1. 坡角
坡面与水平面的夹角叫做坡角,一般用字母α,β,γ表示
2. 坡度 (或坡比)
坡面的铅垂高度 (h) 和水平长度 (l) 的比叫做坡面的坡度 (或坡
比),通常用i表示, 即 i = h : l .
坡面
水平面
坡度等于坡角的正切值,即 ,坡度越大,则坡角越大,山坡就越陡
【提问】什么是坡角?什么是坡度?
探究四
【分析】利用坡度等于坡角的正切值即可求出坡角α和β的度数;在Rt△ABF中,由勾股定理或三角函数定义可得AB的长.
解:(1)在Rt△AFB中,∠AFB=90°
在Rt△CDE中,∠CED=90°
(2)∵AF=6m
∴BF=1.5×6=9m
在Rt△AFB中,
≈10.8
∴斜坡AB的长为10.8m.
【归纳】利用解直角三角形的知识解决实际问题的一般步骤
(1)将实际问题抽象为数学问题(画出平面图形,转化为解直角三角形的问题);
(2)根据问题中的条件,选用合适的锐角三角函数解直角三角形;
(3)得到数学问题的答案;
(4)得到实际问题的答案.
注意:(1)数学问题的解符合实际意义才可以成为实际问题的解.
A
C
D
小结
今天我们学习了哪些知识?
1.了解俯角、仰角、方位角、坡度、坡角等相关概念;
2.能够把实际问题转化为数学问题,建立数学模型,并运用解直角三角形求解.
谢谢观看
28.2.2 应用举例
——第二十八章锐角三角函数
教学目标
01.了解俯角、仰角、方位角、坡度、坡角等相关概念 重点
02.能够把实际问题转化为数学问题,建立数学模型,并运用解直角三角形求解 重难点
上节课我们学习了解直角三角形,在Rt△ABC中除直角外的五个元素之间有什么联系?
(2)两锐角之间的关系:
∠A+∠B=90°
(1)三边之间的关系:
(勾股定理)
(3)边角之间的关系:
上节课我们还对除直角外的五个元素中知道几个元素可以解直角三角形进行了讨论
在直角三角形中,除直角外的五个元素中,已知其中的两个元素(至少有一个是边),可求出其余的未知元素(知二求三)
下面我们开始本节课的学习,解直角三角形在实际问题中的应用
2012年6月18日,“神州”九号载人航天飞船与“天宫”一号目标飞行器成功实现交会对接. “神州”九号与“天宫”一号的组合体在离地球表面343km的圆形轨道上运行. 如图,当组合体运行到离地球表面P点的正上方时,从中能直接看到的地球表面最远的点在什么位置?最远点与P点的距离是多少(地球半径约为6400 km,π取3.142,结果取整数)?
探究一
【问题1】这个实际问题可以抽象成数学图形吗?
可以抽象为以地球中心为圆心、地球半径为半径的⊙O的有关问题.
【问题2】当组合体运行到地球表面P点的正上方时,从中能直接看到的地球表面最远的点在什么位置?
最远点是视线与地球相切时的切点,即点Q.
【问题3】在图中,最远点与P点的距离可以用什么表示?
【分析】从组合体中能直接看到的地球表面最远点,是视线与地球相切时的切点.如图,本题可以抽象为以地球中心为圆心、地球半径为半径的⊙O的有关问题:其中点F是组合体的位置,FQ是⊙O的切线,切点Q是从组合体中观测地球时的最远点, 的长就是地球表面上P,Q两点间的距离.为计算 的长需先求出∠POQ (即α) 的度数
O
F
P
Q
FQ是☉O的切线,∠FQO为直角.
最远点
求PQ的长,要先求∠POQ的度数
⌒
解:设∠POQ= α ,FQ是☉O的切线,△FOQ是直角三角形.
∴ 的长为
热气球的探测器显示,从热气球看一栋楼顶部的仰角为30°,看这栋楼底部的俯角为60°,热气球与楼的水平距离为120 m,这栋楼有多高(结果取整数)?
探究二
【提问】什么是俯角、仰角?
眼睛
水平线
视线
视线
仰角
俯角
仰角:在视线与水平线所成的角中,视线在水平线上方的是仰角.
俯角:在视线与水平线所成的角中,视线在水平线下方的是俯角
热气球的探测器显示,从热气球看一栋楼顶部的仰角为30°,看这栋楼底部的俯角为60°,热气球与楼的水平距离为120 m,这栋楼有多高(结果取整数)?
探究二
【分析】在图中,α=30°,β=60°.
在Rt△ABD中,α =30°,AD=120,所以利用解直角三角形的知识求出BD;类似地可以求出CD,进而求出BC.
探究二
解:如图,a = 30°,β= 60°, AD=120.
答:这栋楼高约为277.1m.
【归纳】解决与仰角、俯角有关的实际问题的方法:
根据仰角、俯角的定义画出水平线、视线,找准仰角、俯角,结合题意,从实际问题情境中抽象出含仰角或俯角的直角三角形,然后利用解直角三角形的方法进行解答.
探究三
如图,一艘海轮位于灯塔P的北偏东65°方向,距离灯塔80 n mile的A 处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东34°方向上的B 处.这时,B处距离灯塔 P有多远(结果取整数)?
65°
34°
P
B
C
A
【提问】同学们对方向角有什么了解?
方向角:指北或指南的方向线与目标线所成的小于90°的角叫做方向角.如图所示
30°
45°
B
O
A
东
西
北
南
45°
45°
西南
O
东北
东
西
北
南
西北
东南
探究三
65°
34°
P
B
C
A
解:如图 ,在Rt△APC中,
PC=PA·cos(90°-65°)
=80×cos25°
≈ 72.505.
在Rt△BPC中,∠B=34°,
因此,当海轮到达位于灯塔P的南偏东34°方向
时,它距离灯塔P大约130n mile.
如图,某水库大坝的横截面为梯形ABCD,AF=DE=6m.斜面坡度i=1:1.5是 指坡面的铅直高度AF与水平宽度BF的比,斜面坡度i=l:3是指DE与CE
的比.根据图中数据,求:
(1)坡角α和β的度数;
(2)斜坡AB的长(结果保留小数点后一位).
探究四
α
l
h
i= h : l
1. 坡角
坡面与水平面的夹角叫做坡角,一般用字母α,β,γ表示
2. 坡度 (或坡比)
坡面的铅垂高度 (h) 和水平长度 (l) 的比叫做坡面的坡度 (或坡
比),通常用i表示, 即 i = h : l .
坡面
水平面
坡度等于坡角的正切值,即 ,坡度越大,则坡角越大,山坡就越陡
【提问】什么是坡角?什么是坡度?
探究四
【分析】利用坡度等于坡角的正切值即可求出坡角α和β的度数;在Rt△ABF中,由勾股定理或三角函数定义可得AB的长.
解:(1)在Rt△AFB中,∠AFB=90°
在Rt△CDE中,∠CED=90°
(2)∵AF=6m
∴BF=1.5×6=9m
在Rt△AFB中,
≈10.8
∴斜坡AB的长为10.8m.
【归纳】利用解直角三角形的知识解决实际问题的一般步骤
(1)将实际问题抽象为数学问题(画出平面图形,转化为解直角三角形的问题);
(2)根据问题中的条件,选用合适的锐角三角函数解直角三角形;
(3)得到数学问题的答案;
(4)得到实际问题的答案.
注意:(1)数学问题的解符合实际意义才可以成为实际问题的解.
A
C
D
小结
今天我们学习了哪些知识?
1.了解俯角、仰角、方位角、坡度、坡角等相关概念;
2.能够把实际问题转化为数学问题,建立数学模型,并运用解直角三角形求解.
谢谢观看
