1.5三角函数的应用——同步练习(含解析) 北师大版九年级数学下册
文档属性
| 名称 | 1.5三角函数的应用——同步练习(含解析) 北师大版九年级数学下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 833.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-19 00:00:00 | ||
图片预览



文档简介
1.5三角函数的应用
1.如图,一把梯子AB长4米,靠在垂直水平地面的墙上,若梯子与地面的夹角为,则梯子底端A到墙面的距离为( )
A. B. C. D.
2.如图,两根竹竿和斜靠在墙上,量得,则竹竿与的长度之比为( )
A. B. C. D.
3.如图,钓鱼竿AC长6 m,露在水面上的鱼线BC长,某钓者想看看鱼钓上的情况,把鱼竿AC转动到的位置,此时露在水面上的鱼线为,则鱼竿转过的角度是( )
A.60° B.45° C.15° D.90°
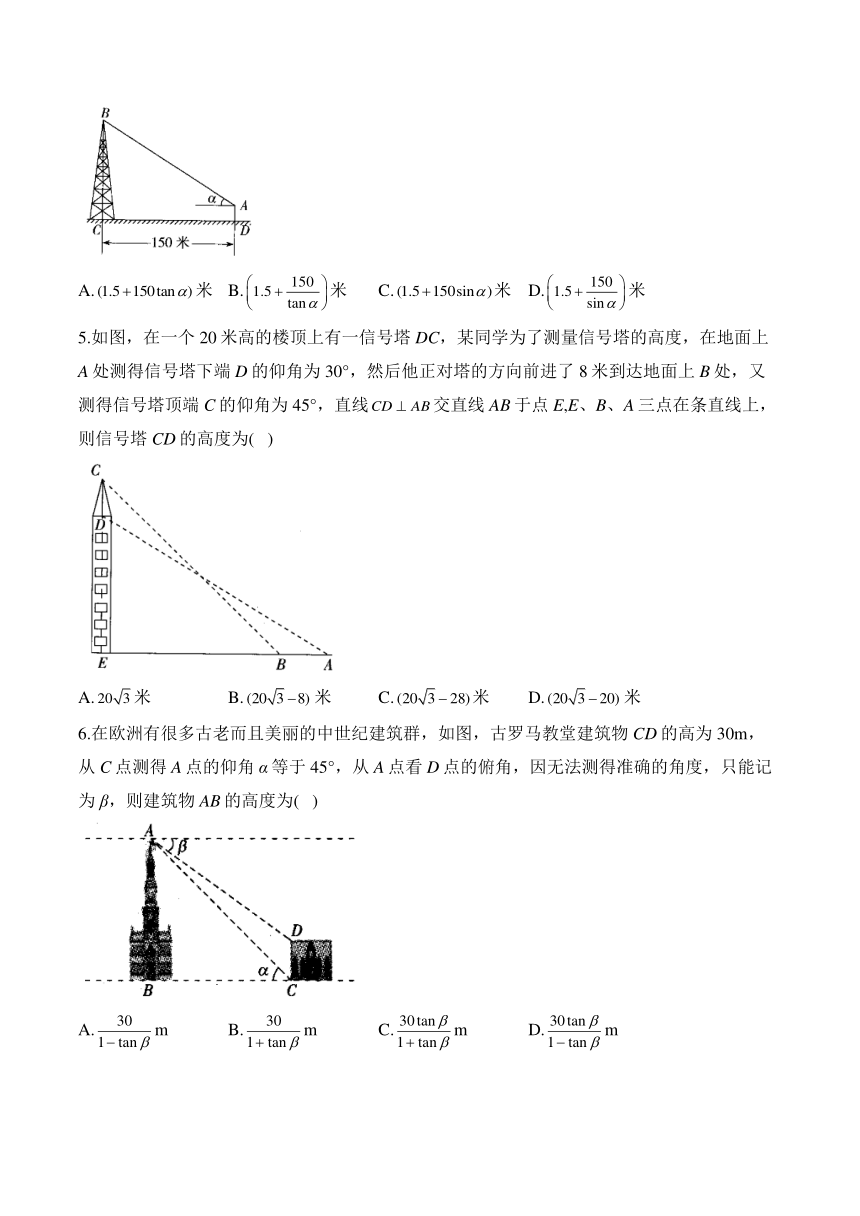
4.如图,在离铁塔150米的A处,用测倾仪测得塔顶的仰角为,测倾仪高AD为1.5米,则铁塔的高BC为( )
A.米 B.米 C.米 D.米
5.如图,在一个20米高的楼顶上有一信号塔DC,某同学为了测量信号塔的高度,在地面上A处测得信号塔下端D的仰角为30°,然后他正对塔的方向前进了8米到达地面上B处,又测得信号塔顶端C的仰角为45°,直线交直线AB于点E,E、B、A三点在条直线上,则信号塔CD的高度为( )
A.米 B.米 C.米 D.米
6.在欧洲有很多古老而且美丽的中世纪建筑群,如图,古罗马教堂建筑物CD的高为30m,从C点测得A点的仰角α等于45°,从A点看D点的俯角,因无法测得准确的角度,只能记为β,则建筑物AB的高度为( )
A.m B.m C.m D.m
7.如图,一艘潜水艇在海面下300 m的点A处发现其正前方的海底C处有黑匣子,同时测得黑匣子C的俯角为30°,潜水艇继续在同一深度直线航行960 m到点B处,测得黑匣子C的俯角为60°,则黑匣子所在的C处距离海面的深度是( )
A. B. C.780 m D.1260 m
8.如图,垂直于水平面的5G信号塔AB建在垂直于水平面的悬崖边B点处,某测量员从山脚C点出发沿水平方向前行78米到D点(点A,B,C在同一直线上),再沿斜坡DE方向前行78米到E点(点A,B,C,D,E在同一平面内),在点E处测得5G信号塔顶端A的仰角为43°,悬崖BC的高为144.5米,斜坡DE的坡度(或坡比),则信号塔AB的高度约为( )
(参考数据:,,)
A.23米 B.24米 C.24.5米 D.25米
9.小明沿着坡度i为的直路向上走了50 m,则小明沿垂直方向升高了_______m.
10.喜迎二十大,“龙舟故里”赛龙舟.丹丹在汨罗江国际龙舟竞渡中心广场点P处观看200米直道竞速赛.如图所示,赛道AB为东西方向,赛道起点A位于点P的北偏西方向上,终点B位于点P的北偏东方向上,米,则点P到赛道AB的距离约为______米(结果保留整数,参考数据:).
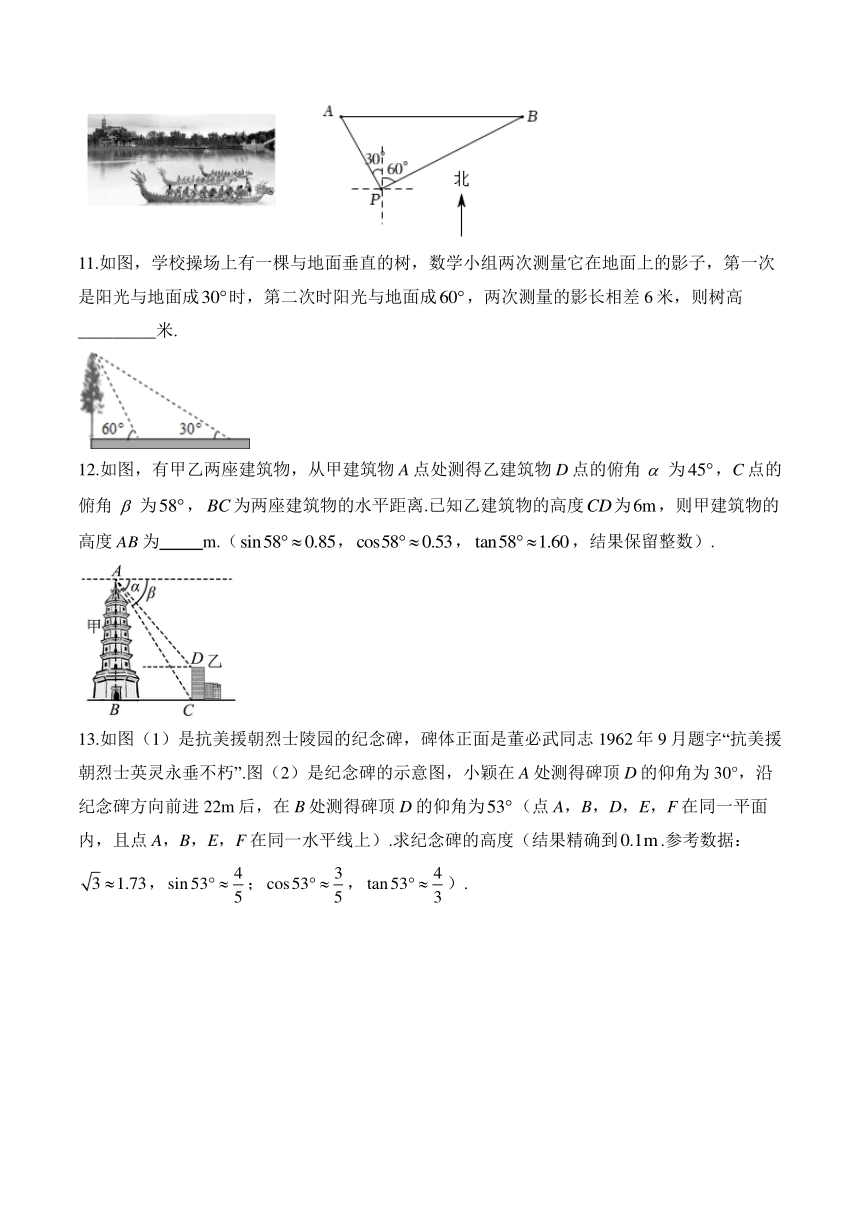
11.如图,学校操场上有一棵与地面垂直的树,数学小组两次测量它在地面上的影子,第一次是阳光与地面成时,第二次时阳光与地面成,两次测量的影长相差6米,则树高_________米.
12.如图,有甲乙两座建筑物,从甲建筑物A点处测得乙建筑物D点的俯角为,C点的俯角为,为两座建筑物的水平距离.已知乙建筑物的高度为,则甲建筑物的高度为_____m.(,,,结果保留整数).
13.如图(1)是抗美援朝烈士陵园的纪念碑,碑体正面是董必武同志1962年9月题字“抗美援朝烈士英灵永垂不朽”.图(2)是纪念碑的示意图,小颖在A处测得碑顶D的仰角为30°,沿纪念碑方向前进22m后,在B处测得碑顶D的仰角为(点A,B,D,E,F在同一平面内,且点A,B,E,F在同一水平线上).求纪念碑的高度(结果精确到.参考数据:,;,).
14.如图,为了测量河对岸A,B两点间距离,数学兴趣小组在河岸南侧选定观测点C,测得A,B均在C的北偏东方向上,沿正东方向行走90米至观测点D,测得A在D的正北方向上,B在D的北偏西方向上.参考数据:,,.
(1)求证:;
(2)求A,B两点间的距离.
答案以及解析
1.答案:A
解析:∠ACB=90°,
cosa=,AC=4cosa米,
故选:A.
2.答案:B
解析:在中,.在中,,所以.
3.答案:C
解析:,
.
,
.
,鱼竿转过的角度是.故选C.
4.答案:A
解析:如图,过点A作,垂足为E,则四边形ADCE为矩形,
米,米.
在中,,米.米.故选A.
5.答案:C
解析:根据题意,得米,米,,.
在中,米,
米.
在中,米,
米.
6.答案:A
解析:如图,作于点E,易知四边形DCBE为矩形,,,.,,.,,在中,,,解得,则建筑物AB的高度为m.故选A.
7.答案:A
解析:如图,过点C向AB作垂线,交AB的延长线于点E,延长CE交海面于点F,易知.
,,,
.
.
.
在中,,
.
.
8.答案:D
解析:如图,过点E作交直线CD于点F,过点E作于点M.
斜坡DE的坡度(或坡比),
设米,,则米.
在中,米,,
即,
解得,(舍去).
米,米.
(米).
米,米.
在中,(米),
(米).
(米).故选D.
9.答案:25
解析:如图,过点B作于点E.
∵坡度.
.
∴小明沿垂直方向升高了25 m.
10.答案:87
解析:解:过点P作,垂足为P,设米,在中,,(米),在中,,(米),米,,,,米,点P到赛道AB的距离约为87米,故答案为:87.
11.答案:
解析:如图所示,
在中,,
,
在中,,
,
,
,
.
故答案为:.
12.答案:16
解析:如图,过D点作于点E,设,
根据题意可得:,,
,
四边形是矩形,
从甲建筑物A点处测得乙建筑物D点的俯角为,C点的俯角为,为两座建筑物的水平距离,乙建筑物的高度为6,
,,,
在中,,
,
,
,
,
,
在中,,
即,
,
解得,
经检验是原分式方程的解且符合题意,
.
故答案为:16.
13.答案:
解析:过D作于H,
如图(2)所示:设,
在中,,
,
在中,,
,
,
解得:,
答:纪念碑的高度约为.
14.答案:(1)见解析
(2)A,B两点间的距离为96米
解析:(1)A,B均在C的北偏东方向上,B在D的北偏西方向上,
结合图形有:,,
,
,
;
(2)A,B均在C的北偏东方向上,A在D的正北方向,且点D在点C的正东方,
是直角三角形,
,
,
在中,,米,
米,
,
,即是直角三角形,
,
米,
米,
答:A,B两点间的距离为96米.
1.如图,一把梯子AB长4米,靠在垂直水平地面的墙上,若梯子与地面的夹角为,则梯子底端A到墙面的距离为( )
A. B. C. D.
2.如图,两根竹竿和斜靠在墙上,量得,则竹竿与的长度之比为( )
A. B. C. D.
3.如图,钓鱼竿AC长6 m,露在水面上的鱼线BC长,某钓者想看看鱼钓上的情况,把鱼竿AC转动到的位置,此时露在水面上的鱼线为,则鱼竿转过的角度是( )
A.60° B.45° C.15° D.90°
4.如图,在离铁塔150米的A处,用测倾仪测得塔顶的仰角为,测倾仪高AD为1.5米,则铁塔的高BC为( )
A.米 B.米 C.米 D.米
5.如图,在一个20米高的楼顶上有一信号塔DC,某同学为了测量信号塔的高度,在地面上A处测得信号塔下端D的仰角为30°,然后他正对塔的方向前进了8米到达地面上B处,又测得信号塔顶端C的仰角为45°,直线交直线AB于点E,E、B、A三点在条直线上,则信号塔CD的高度为( )
A.米 B.米 C.米 D.米
6.在欧洲有很多古老而且美丽的中世纪建筑群,如图,古罗马教堂建筑物CD的高为30m,从C点测得A点的仰角α等于45°,从A点看D点的俯角,因无法测得准确的角度,只能记为β,则建筑物AB的高度为( )
A.m B.m C.m D.m
7.如图,一艘潜水艇在海面下300 m的点A处发现其正前方的海底C处有黑匣子,同时测得黑匣子C的俯角为30°,潜水艇继续在同一深度直线航行960 m到点B处,测得黑匣子C的俯角为60°,则黑匣子所在的C处距离海面的深度是( )
A. B. C.780 m D.1260 m
8.如图,垂直于水平面的5G信号塔AB建在垂直于水平面的悬崖边B点处,某测量员从山脚C点出发沿水平方向前行78米到D点(点A,B,C在同一直线上),再沿斜坡DE方向前行78米到E点(点A,B,C,D,E在同一平面内),在点E处测得5G信号塔顶端A的仰角为43°,悬崖BC的高为144.5米,斜坡DE的坡度(或坡比),则信号塔AB的高度约为( )
(参考数据:,,)
A.23米 B.24米 C.24.5米 D.25米
9.小明沿着坡度i为的直路向上走了50 m,则小明沿垂直方向升高了_______m.
10.喜迎二十大,“龙舟故里”赛龙舟.丹丹在汨罗江国际龙舟竞渡中心广场点P处观看200米直道竞速赛.如图所示,赛道AB为东西方向,赛道起点A位于点P的北偏西方向上,终点B位于点P的北偏东方向上,米,则点P到赛道AB的距离约为______米(结果保留整数,参考数据:).
11.如图,学校操场上有一棵与地面垂直的树,数学小组两次测量它在地面上的影子,第一次是阳光与地面成时,第二次时阳光与地面成,两次测量的影长相差6米,则树高_________米.
12.如图,有甲乙两座建筑物,从甲建筑物A点处测得乙建筑物D点的俯角为,C点的俯角为,为两座建筑物的水平距离.已知乙建筑物的高度为,则甲建筑物的高度为_____m.(,,,结果保留整数).
13.如图(1)是抗美援朝烈士陵园的纪念碑,碑体正面是董必武同志1962年9月题字“抗美援朝烈士英灵永垂不朽”.图(2)是纪念碑的示意图,小颖在A处测得碑顶D的仰角为30°,沿纪念碑方向前进22m后,在B处测得碑顶D的仰角为(点A,B,D,E,F在同一平面内,且点A,B,E,F在同一水平线上).求纪念碑的高度(结果精确到.参考数据:,;,).
14.如图,为了测量河对岸A,B两点间距离,数学兴趣小组在河岸南侧选定观测点C,测得A,B均在C的北偏东方向上,沿正东方向行走90米至观测点D,测得A在D的正北方向上,B在D的北偏西方向上.参考数据:,,.
(1)求证:;
(2)求A,B两点间的距离.
答案以及解析
1.答案:A
解析:∠ACB=90°,
cosa=,AC=4cosa米,
故选:A.
2.答案:B
解析:在中,.在中,,所以.
3.答案:C
解析:,
.
,
.
,鱼竿转过的角度是.故选C.
4.答案:A
解析:如图,过点A作,垂足为E,则四边形ADCE为矩形,
米,米.
在中,,米.米.故选A.
5.答案:C
解析:根据题意,得米,米,,.
在中,米,
米.
在中,米,
米.
6.答案:A
解析:如图,作于点E,易知四边形DCBE为矩形,,,.,,.,,在中,,,解得,则建筑物AB的高度为m.故选A.
7.答案:A
解析:如图,过点C向AB作垂线,交AB的延长线于点E,延长CE交海面于点F,易知.
,,,
.
.
.
在中,,
.
.
8.答案:D
解析:如图,过点E作交直线CD于点F,过点E作于点M.
斜坡DE的坡度(或坡比),
设米,,则米.
在中,米,,
即,
解得,(舍去).
米,米.
(米).
米,米.
在中,(米),
(米).
(米).故选D.
9.答案:25
解析:如图,过点B作于点E.
∵坡度.
.
∴小明沿垂直方向升高了25 m.
10.答案:87
解析:解:过点P作,垂足为P,设米,在中,,(米),在中,,(米),米,,,,米,点P到赛道AB的距离约为87米,故答案为:87.
11.答案:
解析:如图所示,
在中,,
,
在中,,
,
,
,
.
故答案为:.
12.答案:16
解析:如图,过D点作于点E,设,
根据题意可得:,,
,
四边形是矩形,
从甲建筑物A点处测得乙建筑物D点的俯角为,C点的俯角为,为两座建筑物的水平距离,乙建筑物的高度为6,
,,,
在中,,
,
,
,
,
,
在中,,
即,
,
解得,
经检验是原分式方程的解且符合题意,
.
故答案为:16.
13.答案:
解析:过D作于H,
如图(2)所示:设,
在中,,
,
在中,,
,
,
解得:,
答:纪念碑的高度约为.
14.答案:(1)见解析
(2)A,B两点间的距离为96米
解析:(1)A,B均在C的北偏东方向上,B在D的北偏西方向上,
结合图形有:,,
,
,
;
(2)A,B均在C的北偏东方向上,A在D的正北方向,且点D在点C的正东方,
是直角三角形,
,
,
在中,,米,
米,
,
,即是直角三角形,
,
米,
米,
答:A,B两点间的距离为96米.
