北师版七年级数学下册第二章《相交线与平行线》单元检测试卷(含解析)
文档属性
| 名称 | 北师版七年级数学下册第二章《相交线与平行线》单元检测试卷(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-18 18:18:17 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
北师版七年级数学下册第二章《相交线与平行线》单元检测试卷(含解析)
选择题(本大题共有10个小题,每小题4分,共40分)
1.下面四个图形中,∠1与∠2是对顶角的是( )
A. B. C. D.
2. 如图,过直线外一点画已知直线的平行线的方法,其依据是( )
A.同旁内角互补,两直线平行 B.两直线平行,同位角相等
C.同位角相等,两直线平行 D.内错角相等,两直线平行
3. 下列图形中,与不是同位角的是( )
A. B. C. D.
4.如图,直线a,b与直线c,d相交,已知∠1=∠2,∠3=110°,则∠4的度数为( )
A.70° B.80° C.110° D.100°
5.如图,把一块直角三角板的直角顶点放在直尺的一边上,若,则( )
A. B. C. D.
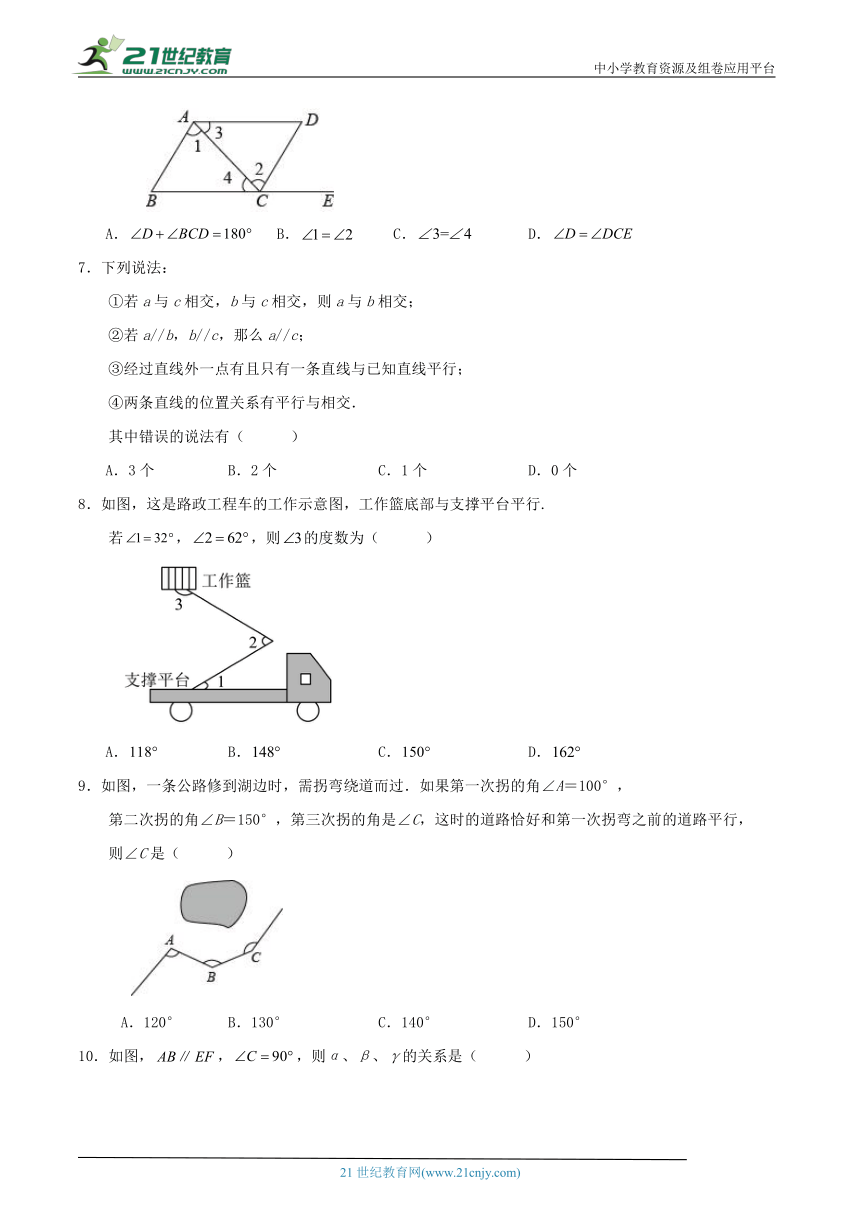
6.如图,下列条件中,不能判定的是( )
A. B. C. D.
7.下列说法:
①若a与c相交,b与c相交,则a与b相交;
②若a//b,b//c,那么a//c;
③经过直线外一点有且只有一条直线与已知直线平行;
④两条直线的位置关系有平行与相交.
其中错误的说法有( )
A.3个 B.2个 C.1个 D.0个
如图,这是路政工程车的工作示意图,工作篮底部与支撑平台平行.
若,,则的度数为( )
A. B. C. D.
如图,一条公路修到湖边时,需拐弯绕道而过.如果第一次拐的角∠A=100°,
第二次拐的角∠B=150°,第三次拐的角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,
则∠C是( )
A.120° B.130° C.140° D.150°
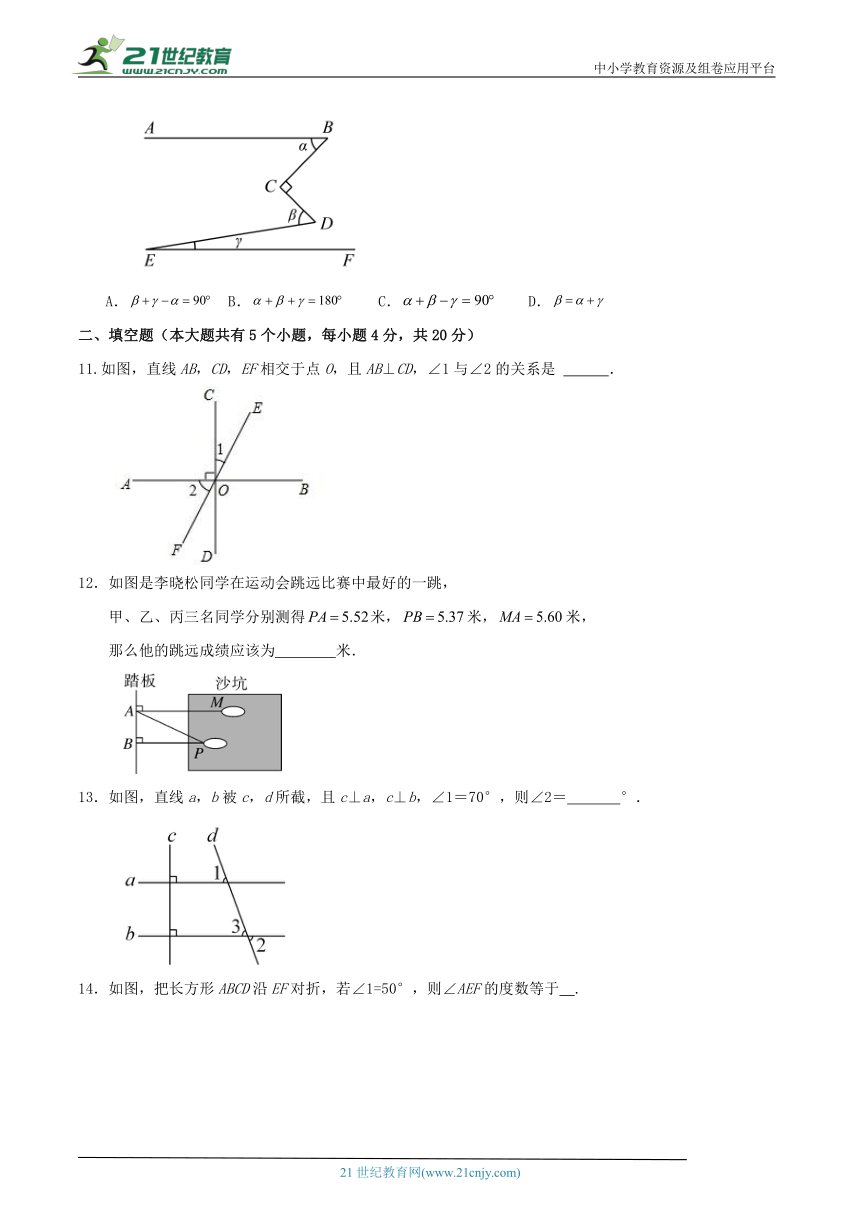
10.如图,,,则α、β、γ的关系是( )
A. B. C. D.
填空题(本大题共有5个小题,每小题4分,共20分)
11.如图,直线AB,CD,EF相交于点O,且AB⊥CD,∠1与∠2的关系是 .
如图是李晓松同学在运动会跳远比赛中最好的一跳,
乙、丙三名同学分别测得米,米,米,
那么他的跳远成绩应该为 米.
13.如图,直线a,b被c,d所截,且c⊥a,c⊥b,∠1=70°,则∠2= °.
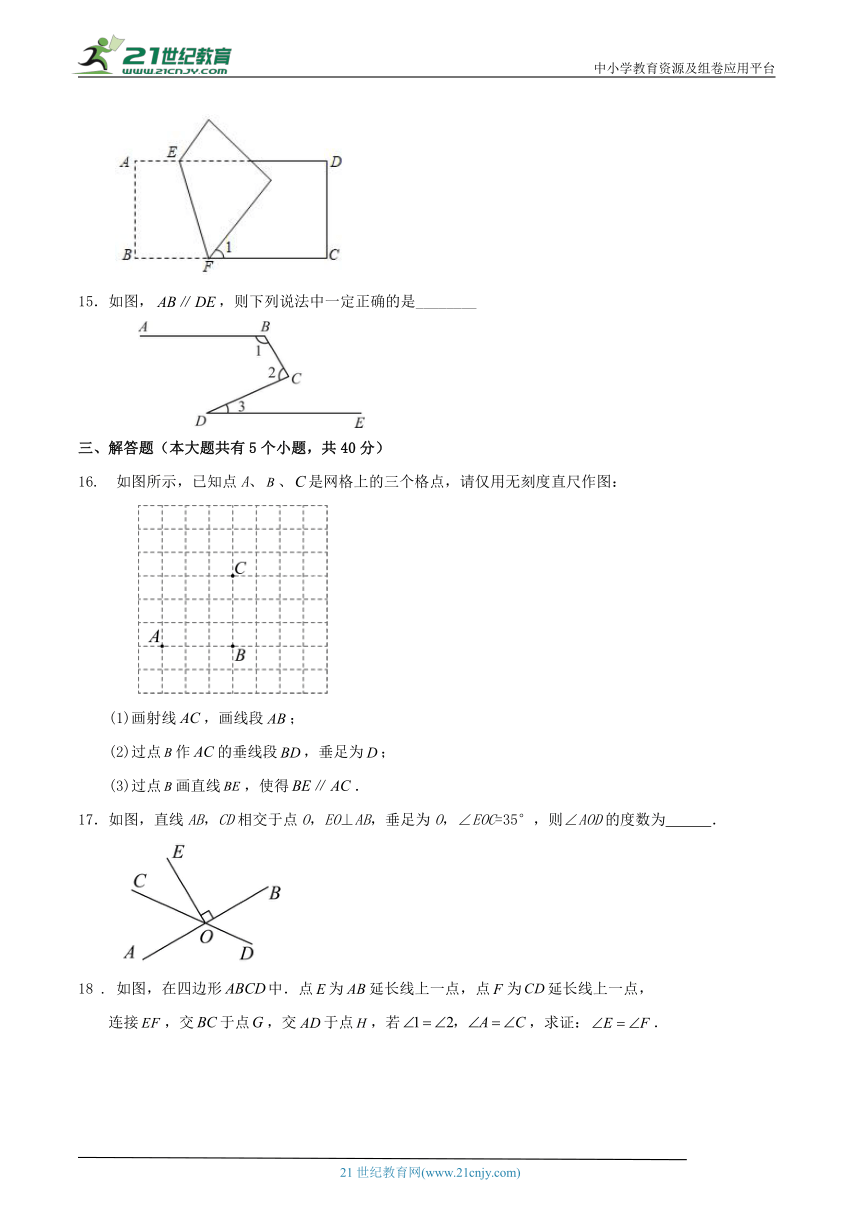
14.如图,把长方形ABCD沿EF对折,若∠1=50°,则∠AEF的度数等于 .
15.如图,,则下列说法中一定正确的是________
解答题(本大题共有5个小题,共40分)
如图所示,已知点A、、是网格上的三个格点,请仅用无刻度直尺作图:
(1)画射线,画线段;
(2)过点作的垂线段,垂足为;
(3)过点画直线,使得.
17.如图,直线AB,CD相交于点O,EO⊥AB,垂足为O,∠EOC=35°,则∠AOD的度数为 .
18 . 如图,在四边形中.点为延长线上一点,点为延长线上一点,
连接,交于点,交于点,若,求证:.
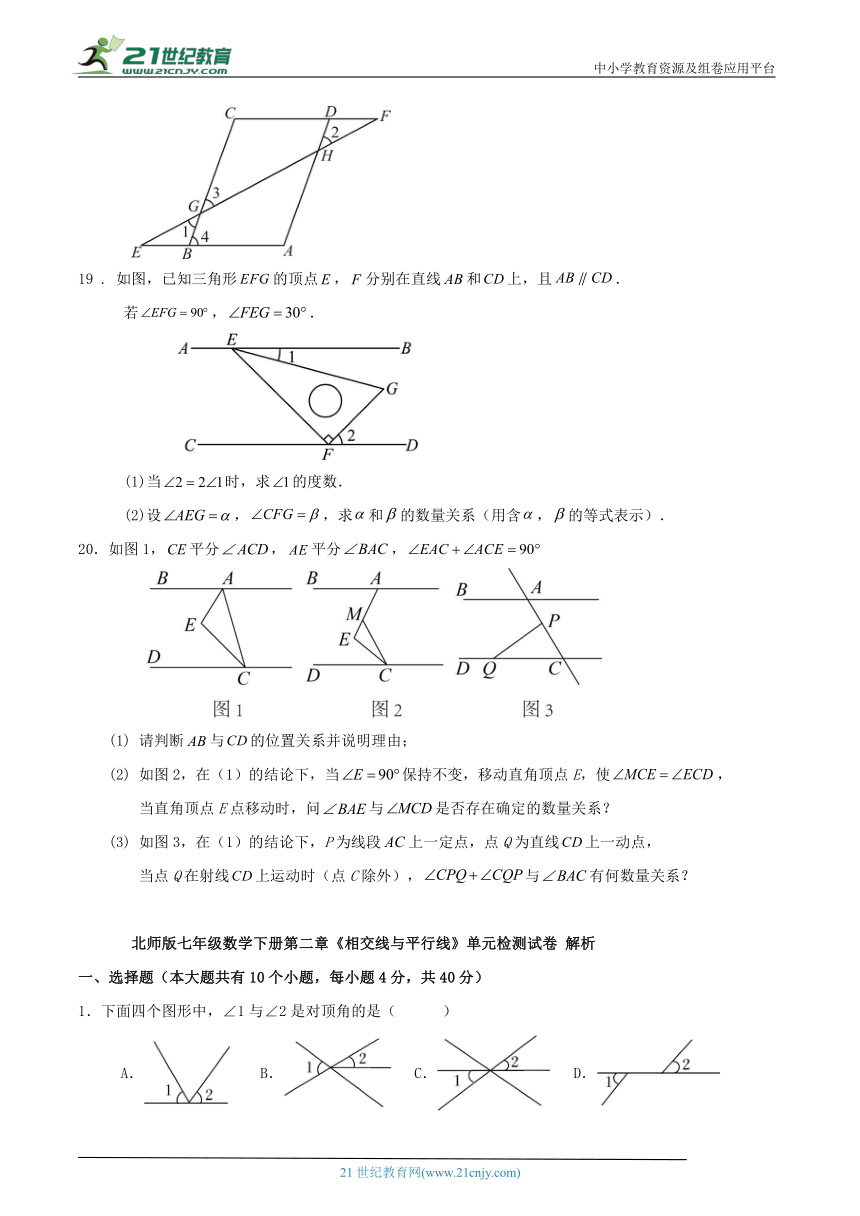
19 . 如图,已知三角形的顶点,分别在直线和上,且.
若,.
(1)当时,求的度数.
(2)设,,求和的数量关系(用含,的等式表示).
20.如图1,平分,平分,
请判断与的位置关系并说明理由;
(2) 如图2,在(1)的结论下,当保持不变,移动直角顶点E,使,
当直角顶点E点移动时,问与是否存在确定的数量关系?
如图3,在(1)的结论下,P为线段上一定点,点Q为直线上一动点,
当点Q在射线上运动时(点C除外),与有何数量关系?
北师版七年级数学下册第二章《相交线与平行线》单元检测试卷 解析
一、选择题(本大题共有10个小题,每小题4分,共40分)
1.下面四个图形中,∠1与∠2是对顶角的是( )
A. B. C. D.
【答案】C
【分析】有公共顶点两角两边互为反向延长线则两角为对顶角.
【详解】A. ∠1、∠2不是对顶角
B. ∠1、∠2不是对顶角
C. ∠1、∠2是对顶角
D. ∠1、∠2不是对顶角
2.如图,过直线外一点画已知直线的平行线的方法,其依据是( )
A.同旁内角互补,两直线平行 B.两直线平行,同位角相等
C.同位角相等,两直线平行 D.内错角相等,两直线平行
【答案】C
【分析】作图时保持∠1=∠2,则可判定两直线平行.
【详解】如图:
∵∠1=∠2,
∴a∥b(同位角相等,两直线平行).
故选:C.
3.下列图形中,与不是同位角的是( )
A. B. C. D.
【答案】C
【分析】同位角的定义:在截线的同侧,并且在被截线的同一方的两个角是同位角.
【详解】解:A图中,∠1与∠2有一边在同一条直线上,另一条边在被截线的同一方,是同位角,不符合题意;
B图中,∠1与∠2有一条边在同一条直线上,另一条边在被截线的同一方,是同位角,不符合题意;
C图中,∠1与∠2的两条边都不在同一条直线上,不是同位角,符合题意;
D图中,∠1与∠2有一边在同一条直线上,另一条边在被截线的同一方,是同位角,不符合题意.
故选:C.
4.如图,直线a,b与直线c,d相交,已知∠1=∠2,∠3=110°,则∠4的度数为( )
A.70° B.80° C.110° D.100°
【答案】A
【详解】解:∵∠3=∠5=110°,∵∠1=∠2=58°,∴a∥b,∴∠4+∠5=180°,∴∠4=70°,
故选A.
5.如图,把一块直角三角板的直角顶点放在直尺的一边上,若,则( )
A. B. C. D.
【答案】B
【分析】由互余可求得的度数,然后由两直线平行,同位角相等求得结果.
【详解】解:如图,
∵,
∴,
∵直尺的两边平行,
∴.
故选:B.
6.如图,下列条件中,不能判定的是( )
A. B. C. D.
【答案】B
【分析】根据平行线的性质进行判断即可.
【详解】解:若,则,,,
∴不能判定的是,故B正确.
故选:B.
7.下列说法:
①若a与c相交,b与c相交,则a与b相交;
②若a//b,b//c,那么a//c;
③经过直线外一点有且只有一条直线与已知直线平行;
④两条直线的位置关系有平行与相交.
其中错误的说法有( )
A.3个 B.2个 C.1个 D.0个
【答案】B
【分析】利用同一个平面内,两条直线的位置关系解答.
【详解】①若a与c相交,b与c相交,则a与b不一定相交;故错误;
②若a∥b,b∥c,那么a∥c;故正确;
③过直线外一点有且只有一条直线与已知直线平行;故正确;
④在同一平面内,两条直线的位置关系有平行、相交两种;故错误.
故选B.
8 . 如图,这是路政工程车的工作示意图,工作篮底部与支撑平台平行.
若,,则的度数为( )
A. B. C. D.
【答案】C
【分析】过点作工作篮底部,根据平行线的性质及角的和差求解即可.
【详解】解:如图,过点作工作篮底部,
,
工作篮底部与支撑平台平行,工作篮底部
支撑平台,
,
,,
,
,
故选:.
9 . 如图,一条公路修到湖边时,需拐弯绕道而过.如果第一次拐的角∠A=100°,
第二次拐的角∠B=150°,第三次拐的角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,
则∠C是( )
A.120° B.130° C.140° D.150°
【答案】B
【分析】首先根据题意作辅助线:过点B作BD∥AE,即可得AE∥BD∥CF,则可求得:∠A=∠1,∠2+∠C=180°,则可求得∠C的值.
【详解】解:过点B作BD∥AE,
∵AE∥CF,
∴AE∥BD∥CF,
∴∠A=∠1,∠2+∠C=180°,
∵∠A=100°,∠1+∠2=∠ABC=150°,
∴∠2=50°,
∴∠C=180°∠2=180°50°=130°,
故选:B.
10.如图,,,则α、β、γ的关系是( )
A. B. C. D.
【答案】C
【分析】过点C、D分别作的平行线、,利用平行线的性质即可解决问题.
【详解】解:如图,过点C、D分别作的平行线、,
∵,
∴,
∴,,,
∵,,
∴,
∴.
故选:C.
二、填空题(本大题共有5个小题,每小题4分,共20分)
11.如图,直线AB,CD,EF相交于点O,且AB⊥CD,∠1与∠2的关系是 .
【答案】互余
【分析】利用对顶角相等可得∠1=∠3,再由∠2+∠3=90°,可得∠1+∠2=90°.
【详解】∵直线AB、EF相交于O点,
∴∠1=∠3.
又∵AB⊥CD,
∴∠2+∠3=90°,
∴∠1+∠2=90°,即∠1与∠2互余.
12 . 如图是李晓松同学在运动会跳远比赛中最好的一跳,
乙、丙三名同学分别测得米,米,米,
那么他的跳远成绩应该为 米.
【答案】
【分析】测量跳远成绩,应从踏板前沿至运动员在沙坑里留下的痕迹的最近点的距离,为运动员的跳远成绩,所以李晓松的跳远成绩为点P到踏板的距离,即点P到踏板所在的直线的垂线段的长度,据此判断出他的跳远成绩应该为多少米即可.
【详解】解:根据跳远规则,李晓松的跳远成绩为点P到踏板的距离,
∵直线外一点到直线的垂线段的长度,叫做点到直线的距离,
∴他的跳远成绩应该为线段的长度,
∵米,
∴他的跳远成绩应该为米.
故答案为:.
13.如图,直线a,b被c,d所截,且c⊥a,c⊥b,∠1=70°,则∠2= °.
【答案】70
【详解】∵c⊥a,c⊥b,
∴a∥b,
∴∠1=∠3,
∵∠2=∠3,
∴∠2=∠1=70°.
故答案为:70
14.如图,把长方形ABCD沿EF对折,若∠1=50°,则∠AEF的度数等于 .
【答案】
【详解】解:∵把长方形ABCD沿EF对折,
∴AD∥BC,∠BFE=∠2,
∵∠1=50°,∠1+∠2+∠BFE=180°,
∴∠BFE==65°,
∵∠AEF+∠BFE=180°,
∴∠AEF=115°.
故答案为:115°.
15.如图,,则下列说法中一定正确的是________
【答案】
【分析】此题要作辅助线,过点作,则根据平行线的传递性,得.先利用,可得,即,再利用,可得,而,整理可得:.
【详解】解:过点作,
,
,
,,
又,
,
.
故答案为:
解答题(本大题共有5个小题,共40分)
16 . 如图所示,已知点A、、是网格上的三个格点,请仅用无刻度直尺作图:
(1)画射线,画线段;
(2)过点作的垂线段,垂足为;
(3)过点画直线,使得.
【答案】(1)见解析
(2)见解析
(3)见解析
【分析】本题考查了射线、线段的作法,画平行线,掌握平行线画法是解题关键.
(1)根据射线及线段的定义作图即可;
(2)过点作的垂线,垂足为D即可;
(3)将C点向右移3个单位得到点E,作直线即可;
【详解】(1)解:射线,线段即为所求;
(2)解:垂线段即为所求;
(3)解:直线即为所求.
17.如图,直线AB,CD相交于点O,EO⊥AB,垂足为O,∠EOC=35°,则∠AOD的度数为 .
【答案】125°
【分析】由两直线垂直,求得∠AOE=90°;由∠AOC与∠EOC互余,∠EOC=35°,即可得到∠AOC的度数;再由∠AOD与∠AOC互补,即可得出∠AOD的度数.
【详解】解:∵EO⊥AB,
∴∠AOE=90°,
又∵∠EOC=35°,
∴∠AOC=∠AOE-∠EOC=90°-35°= 55°,
∴∠AOD=180°-∠AOC=180°-55°=125°,
故答案为:125°.
18 . 如图,在四边形中.点为延长线上一点,点为延长线上一点,
连接,交于点,交于点,若,求证:.
证明:
∵( ),
(已知).
∴ = (等量代换).
∴( ).
∴( ).
∵(已知),
∴(等量代换).
∴ (同旁内角互补,两直线平行).
∴( ).
【答案】对顶角相等;
;
同位角相等,两直线平行;
两直线平行,同旁内角互补;
;两直线平行,内错角相等
【分析】运用平行线的判定与性质进行求解即可得出答案.
【详解】证明:∵(对顶角相等),
(已知),
∴(等量代换),
∴(同位角相等,两直线平行),
∴(两直线平行,同旁内角互补),
∵(已知),
∴(等量代换),
∴(同旁内角互补,两直线平行),
∴(两直线平行,内错角相等),
故答案为:对顶角相等;;同位角相等,两直线平行;两直线平行,同旁内角互补;;两直线平行,内错角相等.
19 . 如图,已知三角形的顶点,分别在直线和上,且.
若,.
(1)当时,求的度数.
(2)设,,求和的数量关系(用含,的等式表示).
【答案】(1)
(2)
【分析】(1)根据两直线平行,同旁内角互补即可求解;
(2)过点过点作,可得,根据两直线平行,同旁内角互补得到,,由此得到,在中,,由此即可求解.
【详解】(1)解:∵,
∴,即,
∵,,,
∴,
∴.
(2)解:如图所示,过点作,
∴,
∵,
∴,
∴,
∴,
即,
∵在中,,,
∴,
∴,
∵,,
∴.
20.如图1,平分,平分,
请判断与的位置关系并说明理由;
(2) 如图2,在(1)的结论下,当保持不变,移动直角顶点E,使,
当直角顶点E点移动时,问与是否存在确定的数量关系?
如图3,在(1)的结论下,P为线段上一定点,点Q为直线上一动点,
当点Q在射线上运动时(点C除外),与有何数量关系?
【答案】(1)平行,证明见解析
(2)存在,
(3)
【分析】(1)先根据CE平分∠ACD,AE平分∠BAC得出∠BAC=2∠EAC,∠ACD=2∠ACE,再由∠EAC+∠ACE=90°可知∠BAC+∠ACD=180,故可得出结论;
(2)过E作EFAB,根据平行线的性质可知EFABCD,∠BAE=∠AEF,∠FEC=∠DCE,故∠BAE+∠ECD=90°,再由∠MCE=∠ECD即可得出结论;
(3)根据ABCD可知∠BAC+∠ACD=180°,∠QPC+∠PQC+∠PCQ=180°,故∠BAC=∠PQC+∠QPC.
【详解】(1)解:平行.
理由如下:
∵平分,平分,
∴,,
∵,
∴,
∴;
(2)解:存在,.
理由如下:
过E作,如图所示:
∵,
∴,
∴,,
∵,
∴,
∵,
∴;
(3)解:∵,
∴,
∵,
∴.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
北师版七年级数学下册第二章《相交线与平行线》单元检测试卷(含解析)
选择题(本大题共有10个小题,每小题4分,共40分)
1.下面四个图形中,∠1与∠2是对顶角的是( )
A. B. C. D.
2. 如图,过直线外一点画已知直线的平行线的方法,其依据是( )
A.同旁内角互补,两直线平行 B.两直线平行,同位角相等
C.同位角相等,两直线平行 D.内错角相等,两直线平行
3. 下列图形中,与不是同位角的是( )
A. B. C. D.
4.如图,直线a,b与直线c,d相交,已知∠1=∠2,∠3=110°,则∠4的度数为( )
A.70° B.80° C.110° D.100°
5.如图,把一块直角三角板的直角顶点放在直尺的一边上,若,则( )
A. B. C. D.
6.如图,下列条件中,不能判定的是( )
A. B. C. D.
7.下列说法:
①若a与c相交,b与c相交,则a与b相交;
②若a//b,b//c,那么a//c;
③经过直线外一点有且只有一条直线与已知直线平行;
④两条直线的位置关系有平行与相交.
其中错误的说法有( )
A.3个 B.2个 C.1个 D.0个
如图,这是路政工程车的工作示意图,工作篮底部与支撑平台平行.
若,,则的度数为( )
A. B. C. D.
如图,一条公路修到湖边时,需拐弯绕道而过.如果第一次拐的角∠A=100°,
第二次拐的角∠B=150°,第三次拐的角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,
则∠C是( )
A.120° B.130° C.140° D.150°
10.如图,,,则α、β、γ的关系是( )
A. B. C. D.
填空题(本大题共有5个小题,每小题4分,共20分)
11.如图,直线AB,CD,EF相交于点O,且AB⊥CD,∠1与∠2的关系是 .
如图是李晓松同学在运动会跳远比赛中最好的一跳,
乙、丙三名同学分别测得米,米,米,
那么他的跳远成绩应该为 米.
13.如图,直线a,b被c,d所截,且c⊥a,c⊥b,∠1=70°,则∠2= °.
14.如图,把长方形ABCD沿EF对折,若∠1=50°,则∠AEF的度数等于 .
15.如图,,则下列说法中一定正确的是________
解答题(本大题共有5个小题,共40分)
如图所示,已知点A、、是网格上的三个格点,请仅用无刻度直尺作图:
(1)画射线,画线段;
(2)过点作的垂线段,垂足为;
(3)过点画直线,使得.
17.如图,直线AB,CD相交于点O,EO⊥AB,垂足为O,∠EOC=35°,则∠AOD的度数为 .
18 . 如图,在四边形中.点为延长线上一点,点为延长线上一点,
连接,交于点,交于点,若,求证:.
19 . 如图,已知三角形的顶点,分别在直线和上,且.
若,.
(1)当时,求的度数.
(2)设,,求和的数量关系(用含,的等式表示).
20.如图1,平分,平分,
请判断与的位置关系并说明理由;
(2) 如图2,在(1)的结论下,当保持不变,移动直角顶点E,使,
当直角顶点E点移动时,问与是否存在确定的数量关系?
如图3,在(1)的结论下,P为线段上一定点,点Q为直线上一动点,
当点Q在射线上运动时(点C除外),与有何数量关系?
北师版七年级数学下册第二章《相交线与平行线》单元检测试卷 解析
一、选择题(本大题共有10个小题,每小题4分,共40分)
1.下面四个图形中,∠1与∠2是对顶角的是( )
A. B. C. D.
【答案】C
【分析】有公共顶点两角两边互为反向延长线则两角为对顶角.
【详解】A. ∠1、∠2不是对顶角
B. ∠1、∠2不是对顶角
C. ∠1、∠2是对顶角
D. ∠1、∠2不是对顶角
2.如图,过直线外一点画已知直线的平行线的方法,其依据是( )
A.同旁内角互补,两直线平行 B.两直线平行,同位角相等
C.同位角相等,两直线平行 D.内错角相等,两直线平行
【答案】C
【分析】作图时保持∠1=∠2,则可判定两直线平行.
【详解】如图:
∵∠1=∠2,
∴a∥b(同位角相等,两直线平行).
故选:C.
3.下列图形中,与不是同位角的是( )
A. B. C. D.
【答案】C
【分析】同位角的定义:在截线的同侧,并且在被截线的同一方的两个角是同位角.
【详解】解:A图中,∠1与∠2有一边在同一条直线上,另一条边在被截线的同一方,是同位角,不符合题意;
B图中,∠1与∠2有一条边在同一条直线上,另一条边在被截线的同一方,是同位角,不符合题意;
C图中,∠1与∠2的两条边都不在同一条直线上,不是同位角,符合题意;
D图中,∠1与∠2有一边在同一条直线上,另一条边在被截线的同一方,是同位角,不符合题意.
故选:C.
4.如图,直线a,b与直线c,d相交,已知∠1=∠2,∠3=110°,则∠4的度数为( )
A.70° B.80° C.110° D.100°
【答案】A
【详解】解:∵∠3=∠5=110°,∵∠1=∠2=58°,∴a∥b,∴∠4+∠5=180°,∴∠4=70°,
故选A.
5.如图,把一块直角三角板的直角顶点放在直尺的一边上,若,则( )
A. B. C. D.
【答案】B
【分析】由互余可求得的度数,然后由两直线平行,同位角相等求得结果.
【详解】解:如图,
∵,
∴,
∵直尺的两边平行,
∴.
故选:B.
6.如图,下列条件中,不能判定的是( )
A. B. C. D.
【答案】B
【分析】根据平行线的性质进行判断即可.
【详解】解:若,则,,,
∴不能判定的是,故B正确.
故选:B.
7.下列说法:
①若a与c相交,b与c相交,则a与b相交;
②若a//b,b//c,那么a//c;
③经过直线外一点有且只有一条直线与已知直线平行;
④两条直线的位置关系有平行与相交.
其中错误的说法有( )
A.3个 B.2个 C.1个 D.0个
【答案】B
【分析】利用同一个平面内,两条直线的位置关系解答.
【详解】①若a与c相交,b与c相交,则a与b不一定相交;故错误;
②若a∥b,b∥c,那么a∥c;故正确;
③过直线外一点有且只有一条直线与已知直线平行;故正确;
④在同一平面内,两条直线的位置关系有平行、相交两种;故错误.
故选B.
8 . 如图,这是路政工程车的工作示意图,工作篮底部与支撑平台平行.
若,,则的度数为( )
A. B. C. D.
【答案】C
【分析】过点作工作篮底部,根据平行线的性质及角的和差求解即可.
【详解】解:如图,过点作工作篮底部,
,
工作篮底部与支撑平台平行,工作篮底部
支撑平台,
,
,,
,
,
故选:.
9 . 如图,一条公路修到湖边时,需拐弯绕道而过.如果第一次拐的角∠A=100°,
第二次拐的角∠B=150°,第三次拐的角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,
则∠C是( )
A.120° B.130° C.140° D.150°
【答案】B
【分析】首先根据题意作辅助线:过点B作BD∥AE,即可得AE∥BD∥CF,则可求得:∠A=∠1,∠2+∠C=180°,则可求得∠C的值.
【详解】解:过点B作BD∥AE,
∵AE∥CF,
∴AE∥BD∥CF,
∴∠A=∠1,∠2+∠C=180°,
∵∠A=100°,∠1+∠2=∠ABC=150°,
∴∠2=50°,
∴∠C=180°∠2=180°50°=130°,
故选:B.
10.如图,,,则α、β、γ的关系是( )
A. B. C. D.
【答案】C
【分析】过点C、D分别作的平行线、,利用平行线的性质即可解决问题.
【详解】解:如图,过点C、D分别作的平行线、,
∵,
∴,
∴,,,
∵,,
∴,
∴.
故选:C.
二、填空题(本大题共有5个小题,每小题4分,共20分)
11.如图,直线AB,CD,EF相交于点O,且AB⊥CD,∠1与∠2的关系是 .
【答案】互余
【分析】利用对顶角相等可得∠1=∠3,再由∠2+∠3=90°,可得∠1+∠2=90°.
【详解】∵直线AB、EF相交于O点,
∴∠1=∠3.
又∵AB⊥CD,
∴∠2+∠3=90°,
∴∠1+∠2=90°,即∠1与∠2互余.
12 . 如图是李晓松同学在运动会跳远比赛中最好的一跳,
乙、丙三名同学分别测得米,米,米,
那么他的跳远成绩应该为 米.
【答案】
【分析】测量跳远成绩,应从踏板前沿至运动员在沙坑里留下的痕迹的最近点的距离,为运动员的跳远成绩,所以李晓松的跳远成绩为点P到踏板的距离,即点P到踏板所在的直线的垂线段的长度,据此判断出他的跳远成绩应该为多少米即可.
【详解】解:根据跳远规则,李晓松的跳远成绩为点P到踏板的距离,
∵直线外一点到直线的垂线段的长度,叫做点到直线的距离,
∴他的跳远成绩应该为线段的长度,
∵米,
∴他的跳远成绩应该为米.
故答案为:.
13.如图,直线a,b被c,d所截,且c⊥a,c⊥b,∠1=70°,则∠2= °.
【答案】70
【详解】∵c⊥a,c⊥b,
∴a∥b,
∴∠1=∠3,
∵∠2=∠3,
∴∠2=∠1=70°.
故答案为:70
14.如图,把长方形ABCD沿EF对折,若∠1=50°,则∠AEF的度数等于 .
【答案】
【详解】解:∵把长方形ABCD沿EF对折,
∴AD∥BC,∠BFE=∠2,
∵∠1=50°,∠1+∠2+∠BFE=180°,
∴∠BFE==65°,
∵∠AEF+∠BFE=180°,
∴∠AEF=115°.
故答案为:115°.
15.如图,,则下列说法中一定正确的是________
【答案】
【分析】此题要作辅助线,过点作,则根据平行线的传递性,得.先利用,可得,即,再利用,可得,而,整理可得:.
【详解】解:过点作,
,
,
,,
又,
,
.
故答案为:
解答题(本大题共有5个小题,共40分)
16 . 如图所示,已知点A、、是网格上的三个格点,请仅用无刻度直尺作图:
(1)画射线,画线段;
(2)过点作的垂线段,垂足为;
(3)过点画直线,使得.
【答案】(1)见解析
(2)见解析
(3)见解析
【分析】本题考查了射线、线段的作法,画平行线,掌握平行线画法是解题关键.
(1)根据射线及线段的定义作图即可;
(2)过点作的垂线,垂足为D即可;
(3)将C点向右移3个单位得到点E,作直线即可;
【详解】(1)解:射线,线段即为所求;
(2)解:垂线段即为所求;
(3)解:直线即为所求.
17.如图,直线AB,CD相交于点O,EO⊥AB,垂足为O,∠EOC=35°,则∠AOD的度数为 .
【答案】125°
【分析】由两直线垂直,求得∠AOE=90°;由∠AOC与∠EOC互余,∠EOC=35°,即可得到∠AOC的度数;再由∠AOD与∠AOC互补,即可得出∠AOD的度数.
【详解】解:∵EO⊥AB,
∴∠AOE=90°,
又∵∠EOC=35°,
∴∠AOC=∠AOE-∠EOC=90°-35°= 55°,
∴∠AOD=180°-∠AOC=180°-55°=125°,
故答案为:125°.
18 . 如图,在四边形中.点为延长线上一点,点为延长线上一点,
连接,交于点,交于点,若,求证:.
证明:
∵( ),
(已知).
∴ = (等量代换).
∴( ).
∴( ).
∵(已知),
∴(等量代换).
∴ (同旁内角互补,两直线平行).
∴( ).
【答案】对顶角相等;
;
同位角相等,两直线平行;
两直线平行,同旁内角互补;
;两直线平行,内错角相等
【分析】运用平行线的判定与性质进行求解即可得出答案.
【详解】证明:∵(对顶角相等),
(已知),
∴(等量代换),
∴(同位角相等,两直线平行),
∴(两直线平行,同旁内角互补),
∵(已知),
∴(等量代换),
∴(同旁内角互补,两直线平行),
∴(两直线平行,内错角相等),
故答案为:对顶角相等;;同位角相等,两直线平行;两直线平行,同旁内角互补;;两直线平行,内错角相等.
19 . 如图,已知三角形的顶点,分别在直线和上,且.
若,.
(1)当时,求的度数.
(2)设,,求和的数量关系(用含,的等式表示).
【答案】(1)
(2)
【分析】(1)根据两直线平行,同旁内角互补即可求解;
(2)过点过点作,可得,根据两直线平行,同旁内角互补得到,,由此得到,在中,,由此即可求解.
【详解】(1)解:∵,
∴,即,
∵,,,
∴,
∴.
(2)解:如图所示,过点作,
∴,
∵,
∴,
∴,
∴,
即,
∵在中,,,
∴,
∴,
∵,,
∴.
20.如图1,平分,平分,
请判断与的位置关系并说明理由;
(2) 如图2,在(1)的结论下,当保持不变,移动直角顶点E,使,
当直角顶点E点移动时,问与是否存在确定的数量关系?
如图3,在(1)的结论下,P为线段上一定点,点Q为直线上一动点,
当点Q在射线上运动时(点C除外),与有何数量关系?
【答案】(1)平行,证明见解析
(2)存在,
(3)
【分析】(1)先根据CE平分∠ACD,AE平分∠BAC得出∠BAC=2∠EAC,∠ACD=2∠ACE,再由∠EAC+∠ACE=90°可知∠BAC+∠ACD=180,故可得出结论;
(2)过E作EFAB,根据平行线的性质可知EFABCD,∠BAE=∠AEF,∠FEC=∠DCE,故∠BAE+∠ECD=90°,再由∠MCE=∠ECD即可得出结论;
(3)根据ABCD可知∠BAC+∠ACD=180°,∠QPC+∠PQC+∠PCQ=180°,故∠BAC=∠PQC+∠QPC.
【详解】(1)解:平行.
理由如下:
∵平分,平分,
∴,,
∵,
∴,
∴;
(2)解:存在,.
理由如下:
过E作,如图所示:
∵,
∴,
∴,,
∵,
∴,
∵,
∴;
(3)解:∵,
∴,
∵,
∴.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
