初中数学华师大版七年级下册7.1 二元一次方程组和它的解课件(19张PPT)
文档属性
| 名称 | 初中数学华师大版七年级下册7.1 二元一次方程组和它的解课件(19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 400.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-19 13:55:41 | ||
图片预览






文档简介
(共19张PPT)
第七章 一次方程组
7.1 二元一次方程组和它的解
学习导航
学习目标
合作探究
当堂检测
课堂总结
自主学习
新课导入
一、学习目标
1.了解二元一次方程、二元一次方程组及其解的概念,会判断一组数是不是某个二元一次方程组的解;(重点)
2.能根据实际情境列出二元一次方程组.(难点)
二、新课导入
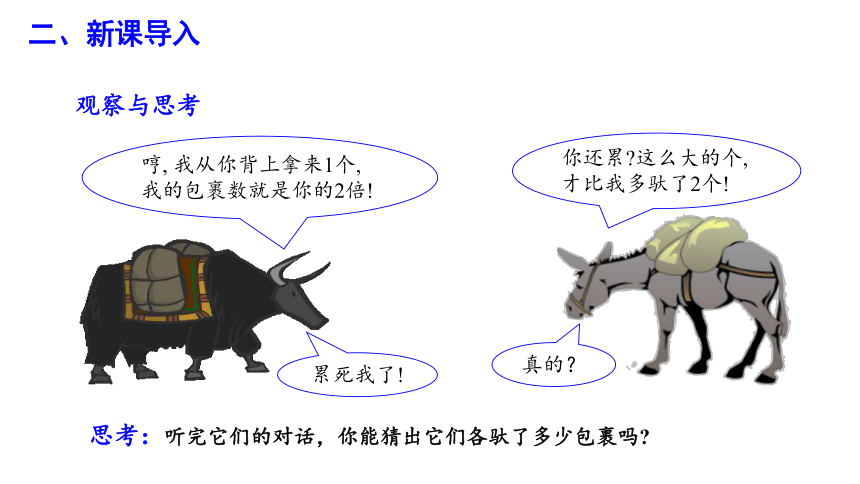
观察与思考
真的?
你还累 这么大的个,才比我多驮了2个!
累死我了!
哼, 我从你背上拿来1个,我的包裹数就是你的2倍!
思考:听完它们的对话,你能猜出它们各驮了多少包裹吗
知识点1:二元一次方程及二元一次方程组的概念
三、自主学习
问题1:设老牛驮了x个包裹 , 小马驮了y个包裹. 你能根据它们的对话列出方程吗?
分析:找出等量关系,列出方程即可.
老牛从小马的背上拿来1个包裹,就是小马的2倍,即:
x - y = 2;
x + 1 = 2 ( y-1 ).
解:老牛的包裹数比小马的多2个,即:
知识点1:二元一次方程及二元一次方程组的概念
三、自主学习
问题2:观察问题1列出的方程,回答下列问题:
方程:x - y = 2 和 x + 1 = 2 ( y-1 ).
(1)上面所列方程各含有几个未知数;(2)含有未知数的项的次数是多少.
(2)次数都是1.
解:(1)2个未知数;
思考:含有上述特点的方程是什么方程?上述两个方程能组合在一起吗?
总结:二元一次方程及二元一次方程组
1. 含有两个未知数,并且含未知数项的次数都是1,这样的整式方程,叫做二元一次方程;
2. 把含有相同未知数的两个二元一次方程合在一起,就组成了一个二元一次方程组.
知识点1:二元一次方程及二元一次方程组的概念
三、自主学习
注意:方程组各方程中同一字母必须代表同一个量.
思考:二元一次方程和一元一次方程有何异同,请将它们填入下表:
一元一次方程的特征 二元一次方程的特征
只含有一个未知数 含有 个未知数
含有未知数的项的次数是一次 含有未知数的项的次数是 次
方程两边都是整式 方程两边都是 式
整
两
一
知识点1:二元一次方程及二元一次方程组的概念
三、自主学习
(1)例如:x=5 ,y=3 是方程 x+y=8 的一个解,记作: ;
知识点2:二元一次方程组的解及列二元一次方程组
三、自主学习
问题3:(1)x=5,y=3适合方程 x+y=8 吗? x=6,y=2呢?你还能找到其他x,y的值适合方程 x+y=8 吗
(2)x=5,y=3 适合方程 5x+3y=34 吗?x=6,y=2呢?
分析:适合一个二元一次方程的一组未知数的值,叫做这个二元一次方程的一个解.
x=5
y=3
x=6 ,y=2 是方程 x+y=8 的一个解,记作: ;
x=6
y=2
(2)例如:x=5 ,y=3 是方程 5x+3y=34 的一个解,记作: ;
知识点2:二元一次方程组的解及列二元一次方程组
三、自主学习
问题3:(2)x=5,y=3 适合方程 5x+3y=34 吗?x=6,y=2呢?
x=5
y=3
x=6 ,y=2 不是方程 5x+3y=34 的一个解.
思考:仔细观察问题 3 (1)、(2) 问,同学们有什么发现吗?
知识点2:二元一次方程组的解及列二元一次方程组
三、自主学习
总结:二元一次方程及二元一次方程组的解
1. 二元一次方程的解:
① 适合二元一次方程的一组未知数的值,叫做这个二元一次方程的一个解;
② 二元一次方程可以有很多个解;
2. 二元一次方程组的解:使二元一次方程组中两个方程的左右两边的值都相等的两个未知数的值,叫做这个二元一次方程组的解.
例:x=5 ,y=3 和 x=6 ,y=2 都是方程 x+y=8 的一个解;
四、合作探究
探究一:二元一次方程组及其解
活动1:若,是方程组 的解,则a、b的值分别为多少?
分析: 将数据分别代入即可.
解:将 代入方程组 ;
得 ,
解得
四、合作探究
练一练:
1.若 是二元一次方程组的解,则这个方程组是( )
A. B. C. D.
D
分析:将x = 2,y = -1分别代入选项方程组中,要同时满足两个二元一次方程的解,即是这个二元一次方程组的解.
四、合作探究
探究二:列二元一次方程组
活动2:小戴同学用10元钱购买了甲、乙两种贺卡共8张,单价分别是1元与2元.请问小戴同学分别买了几张甲贺卡和几张乙贺卡?(列出方程即可)
问题探究:由题可知两个等量关系:① 甲贺卡数量 + 乙贺卡数量 = 张;
② 1 × 贺卡数量 + 2 × 贺卡数量 = 10元.
问题解决:设他购买了1元的贺卡x张,2元的贺卡y张;
根据题意得: .
8
甲
乙
2. 根据题意列方程组:某校有两种类型的学生宿舍21间,大的宿舍每间可住6人,小的宿舍每间可住3人. 该校96个住宿生恰好住满这21间宿舍. 大、小宿舍各有多少间
解:设大宿舍有x间,小宿舍有y间,则有: .
分析:从题目中找到两个等量关系即可.
四、合作探究
练一练:
五、当堂检测
分析:A中有三个未知数,所以是三元方程;B中未知项的次数为2;C中含未知数的项不是整式.故选D.
D
1. 下列方程中,是二元一次方程的是( )
A. B. C. D.
紧扣相关概念
2.下列方程组是二元一次方程组的是( )
A. B.
C. D.
B
五、当堂检测
3. 将一摞笔记本分给若干同学. 每个同学4本,则剩下6本;每个同学6本,又差了3本. 请问共有多少个笔记本、多少个同学?(列出方程即可)
分析:从实际问题中列二元一次方程组,关键是从题目中找到两个等量关系.
解:设有x个同学,y个笔记本,则有: .
五、当堂检测
六、课堂总结
第七章 一次方程组
7.1 二元一次方程组和它的解
学习导航
学习目标
合作探究
当堂检测
课堂总结
自主学习
新课导入
一、学习目标
1.了解二元一次方程、二元一次方程组及其解的概念,会判断一组数是不是某个二元一次方程组的解;(重点)
2.能根据实际情境列出二元一次方程组.(难点)
二、新课导入
观察与思考
真的?
你还累 这么大的个,才比我多驮了2个!
累死我了!
哼, 我从你背上拿来1个,我的包裹数就是你的2倍!
思考:听完它们的对话,你能猜出它们各驮了多少包裹吗
知识点1:二元一次方程及二元一次方程组的概念
三、自主学习
问题1:设老牛驮了x个包裹 , 小马驮了y个包裹. 你能根据它们的对话列出方程吗?
分析:找出等量关系,列出方程即可.
老牛从小马的背上拿来1个包裹,就是小马的2倍,即:
x - y = 2;
x + 1 = 2 ( y-1 ).
解:老牛的包裹数比小马的多2个,即:
知识点1:二元一次方程及二元一次方程组的概念
三、自主学习
问题2:观察问题1列出的方程,回答下列问题:
方程:x - y = 2 和 x + 1 = 2 ( y-1 ).
(1)上面所列方程各含有几个未知数;(2)含有未知数的项的次数是多少.
(2)次数都是1.
解:(1)2个未知数;
思考:含有上述特点的方程是什么方程?上述两个方程能组合在一起吗?
总结:二元一次方程及二元一次方程组
1. 含有两个未知数,并且含未知数项的次数都是1,这样的整式方程,叫做二元一次方程;
2. 把含有相同未知数的两个二元一次方程合在一起,就组成了一个二元一次方程组.
知识点1:二元一次方程及二元一次方程组的概念
三、自主学习
注意:方程组各方程中同一字母必须代表同一个量.
思考:二元一次方程和一元一次方程有何异同,请将它们填入下表:
一元一次方程的特征 二元一次方程的特征
只含有一个未知数 含有 个未知数
含有未知数的项的次数是一次 含有未知数的项的次数是 次
方程两边都是整式 方程两边都是 式
整
两
一
知识点1:二元一次方程及二元一次方程组的概念
三、自主学习
(1)例如:x=5 ,y=3 是方程 x+y=8 的一个解,记作: ;
知识点2:二元一次方程组的解及列二元一次方程组
三、自主学习
问题3:(1)x=5,y=3适合方程 x+y=8 吗? x=6,y=2呢?你还能找到其他x,y的值适合方程 x+y=8 吗
(2)x=5,y=3 适合方程 5x+3y=34 吗?x=6,y=2呢?
分析:适合一个二元一次方程的一组未知数的值,叫做这个二元一次方程的一个解.
x=5
y=3
x=6 ,y=2 是方程 x+y=8 的一个解,记作: ;
x=6
y=2
(2)例如:x=5 ,y=3 是方程 5x+3y=34 的一个解,记作: ;
知识点2:二元一次方程组的解及列二元一次方程组
三、自主学习
问题3:(2)x=5,y=3 适合方程 5x+3y=34 吗?x=6,y=2呢?
x=5
y=3
x=6 ,y=2 不是方程 5x+3y=34 的一个解.
思考:仔细观察问题 3 (1)、(2) 问,同学们有什么发现吗?
知识点2:二元一次方程组的解及列二元一次方程组
三、自主学习
总结:二元一次方程及二元一次方程组的解
1. 二元一次方程的解:
① 适合二元一次方程的一组未知数的值,叫做这个二元一次方程的一个解;
② 二元一次方程可以有很多个解;
2. 二元一次方程组的解:使二元一次方程组中两个方程的左右两边的值都相等的两个未知数的值,叫做这个二元一次方程组的解.
例:x=5 ,y=3 和 x=6 ,y=2 都是方程 x+y=8 的一个解;
四、合作探究
探究一:二元一次方程组及其解
活动1:若,是方程组 的解,则a、b的值分别为多少?
分析: 将数据分别代入即可.
解:将 代入方程组 ;
得 ,
解得
四、合作探究
练一练:
1.若 是二元一次方程组的解,则这个方程组是( )
A. B. C. D.
D
分析:将x = 2,y = -1分别代入选项方程组中,要同时满足两个二元一次方程的解,即是这个二元一次方程组的解.
四、合作探究
探究二:列二元一次方程组
活动2:小戴同学用10元钱购买了甲、乙两种贺卡共8张,单价分别是1元与2元.请问小戴同学分别买了几张甲贺卡和几张乙贺卡?(列出方程即可)
问题探究:由题可知两个等量关系:① 甲贺卡数量 + 乙贺卡数量 = 张;
② 1 × 贺卡数量 + 2 × 贺卡数量 = 10元.
问题解决:设他购买了1元的贺卡x张,2元的贺卡y张;
根据题意得: .
8
甲
乙
2. 根据题意列方程组:某校有两种类型的学生宿舍21间,大的宿舍每间可住6人,小的宿舍每间可住3人. 该校96个住宿生恰好住满这21间宿舍. 大、小宿舍各有多少间
解:设大宿舍有x间,小宿舍有y间,则有: .
分析:从题目中找到两个等量关系即可.
四、合作探究
练一练:
五、当堂检测
分析:A中有三个未知数,所以是三元方程;B中未知项的次数为2;C中含未知数的项不是整式.故选D.
D
1. 下列方程中,是二元一次方程的是( )
A. B. C. D.
紧扣相关概念
2.下列方程组是二元一次方程组的是( )
A. B.
C. D.
B
五、当堂检测
3. 将一摞笔记本分给若干同学. 每个同学4本,则剩下6本;每个同学6本,又差了3本. 请问共有多少个笔记本、多少个同学?(列出方程即可)
分析:从实际问题中列二元一次方程组,关键是从题目中找到两个等量关系.
解:设有x个同学,y个笔记本,则有: .
五、当堂检测
六、课堂总结
