2023-2024学年北师大版九年级下册3.6直线与圆的位置关系 同步练习(含解析)
文档属性
| 名称 | 2023-2024学年北师大版九年级下册3.6直线与圆的位置关系 同步练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 568.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-19 16:41:43 | ||
图片预览




文档简介
2023-2024学年北师大版九年级下册同步练习【提升卷】
3.6直线与圆的位置关系 同步练习
姓名: 班级:
一、选择题
1.若直线l与☉O有公共点,则直线l与☉O的位置关系可能是( )
A.相交或相切 B.相交或相离 C.相切或相离 D.无法确定
2.已知⊙O的半径为6cm,圆心O到直线l的距离为5cm,则直线l与⊙O的交点个数为( )
A.0 B.l C.2 D.无法确定
3.已知在平面直角坐标系中,圆P的圆心坐标为(4,5),半径为3个单位长度,把圆P沿水平方向向左平移d个单位长度后恰好与y轴相切,则d的值是( )
A.1 B.2 C.2或8 D.1或7
4.如图,点P为⊙O外一点,PA为⊙O的切线,A为切点,PO交⊙O于点B,∠P=30°,OB=3,则线段BP的长为( )
A.3 B.3 C.6 D.9
5.在平面直角坐标系xOy中,经过点(sin45°,cos30°)的直线,与以原点为圆心,2为半径的圆的位置关系是( )
A.相交 B.相切
C.相离 D.以上三者都有可能
6.已知⊙O的直径为12cm,圆心到直线l的距离为6cm,则直线l与⊙O的位置关系是( )
A.相离 B.相切 C.相交 D.无法确定
7.如图,PA、PB是⊙O的两条切线,切点是A、B.如果OP=4,PA=2,那么∠AOB等于( )
A.90° B.100° C.110° D.120°
8.如图,BC是⊙O的直径,AD是⊙O的切线,切点为D,AD与CB的延长线交于点A,∠C=30°,给出下面四个结论:
①AD=DC;②AB=BD;③AB= BC;④BD=CD,
其中正确的个数为( )
A.4个 B.3个 C.2个 D.1个
9.如图,两个同心圆,大圆的半径为5,小圆的半径为3,若大圆的弦AB与小圆有公共点,则弦AB的取值范围是( )
A.8≤AB≤10 B.8<AB≤10 C.4≤AB≤5 D.4<AB≤5
10.已知△ABC中,AB=AC=6cm,BC=8cm,以点A为圆心,以4cm长为半径作圆,则⊙A与BC的位置关系是( )
A.相离 B.相切 C.相交 D.外离
11.在平面直角坐标系中,以点(-3,4)为圆心,4为半径的圆( )
A.与x轴相交,与y轴相切 B.与x轴相离,与y轴相交
C.与x轴相切,与y轴相离 D.与x轴相切,与y轴相交
12.在平面直角坐标系内,以原点O为圆心,1为半径作圆,点P在直线y= 上运动,过点P作该圆的一条切线,切点为A,则PA的最小值为( )
A.3 B.2 C. D.
二、填空题
13.若⊙O的半径为4cm,圆心O到直线l的距离为5cm,则直线l与⊙O的位置关系是 .
14.⊙O直径为8cm,有M、N、P三点,OM=4cm,ON=8cm,OP=2cm,则M点在 ,N点在圆 ,P点在圆 。
15.如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,若∠C=20°,则∠CDA= °.
16.如图,△ABC中,∠ACB=90°,sinA= ,AC=12,将△ABC绕点C顺时针旋转90°得到△A'B'C,P为线段A′B'上的动点,以点P为圆心,PA′长为半径作⊙P,当⊙P与△ABC的边相切时,⊙P的半径为 .
在Rt△ABC中,∠C=90°,AC=3,BC=4.若以C点为圆心,r为半径所作的圆与斜边AB只有一个公共点,则r的取值范围是 .
三、解答题
18.如图所示,Rt△ABC中,∠ACB=90°,CA=6,CB=8,以C为圆心,r为半径作⊙C,当r为多少时,⊙C与AB相切?
19.如图,⊙O的半径为3cm,弦AC=4 cm,AB=4cm,若以O为圆心,再作一个圆与AC相切,则这个圆的半径为多少?这个圆与AB的位置关系如何?
20.如图,已知点O为Rt△ABC斜边AC上一点,以点O为圆心,OA长为半径的⊙O与BC相切于点E,与AC相交于点D,连接AE.
求证:AE平分∠CAB;
在南部沿海某气象站A测得一热带风暴从A的南偏东30°的方向迎着气象站袭来,已知该风暴速度为每小时20千米,风暴周围50千米范围内将受到影响,若该风暴不改变速度与方向,问气象站正南方60千米处的沿海城市B是否会受这次风暴的影响?若不受影响,请说明理由;若受影响,请求出受影响的时间.
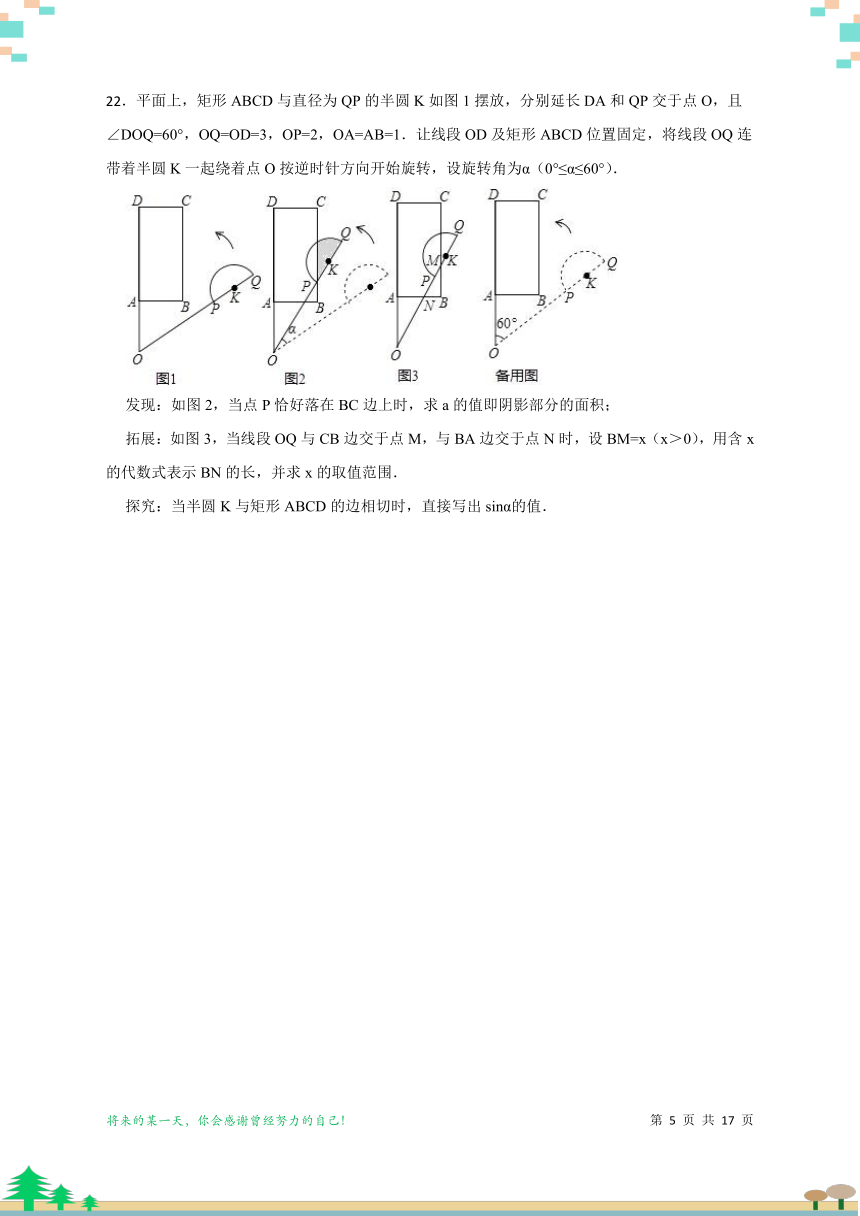
22.平面上,矩形ABCD与直径为QP的半圆K如图1摆放,分别延长DA和QP交于点O,且∠DOQ=60°,OQ=OD=3,OP=2,OA=AB=1.让线段OD及矩形ABCD位置固定,将线段OQ连带着半圆K一起绕着点O按逆时针方向开始旋转,设旋转角为α(0°≤α≤60°).
发现:如图2,当点P恰好落在BC边上时,求a的值即阴影部分的面积;
拓展:如图3,当线段OQ与CB边交于点M,与BA边交于点N时,设BM=x(x>0),用含x的代数式表示BN的长,并求x的取值范围.
探究:当半圆K与矩形ABCD的边相切时,直接写出sinα的值.
答案解析部分
1.答案:A
解析:解 :①一个公共点,直线与圆相切,②两个公共点,直线与圆相交。
故答案为:相交或相切。
分析:分直线与圆公共点的个数来讨论:①一个公共点,直线与圆相切,②两个公共点,直线与圆相交。
2.答案:C
解析:∵⊙O的半径为6cm,圆心O到直线l的距离为5cm,6cm>5cm,
∴直线l与⊙O相交,
∴直线l与⊙O有两个交点.
故答案为:C.
分析:直线和圆的位置关系是:圆心到直线的距离小于半径时,直线与圆相交,直线与圆有两个公共点,所以由题意可得直线l与圆相交,于是可知;直线l与⊙O有两个交点。
3.答案:D
解析:当⊙p在原点右侧与y轴相切时,x-d=r,
∴d=x-r=1.
当⊙p在原点左侧与y轴相切时,
x+r=d,
∴d=7,
所以d的值是1或7.
故答案为:D.
分析:由题意可知:圆P平移前在y轴的右侧,所以有两种情况:
①当⊙p在原点右侧与y轴相切时,根据直线和圆的位置关系,当圆心P到直线的距离等于半径时,直线和圆相切,可求解;
②当⊙p在原点左侧与y轴相切时,同理可求解。综合两种情况可判断选项。
4.答案:A
解析:解:连接OA,
∵PA为⊙O的切线,
∴∠OAP=90°,
∵∠P=30°,OB=3,
∴AO=3,则OP=6,
故BP=6﹣3=3.
故答案为:A.
分析:连接OA,根据切线垂直于经过切点的半径得出∠OAP=90°,根据含30°直角三角形的边之间的关系得出OP的长,最后根据BP=OP-OB即可算出答案。
5.答案:A
解析:解:设直线经过的点为A,
∵点A的坐标为(sin45°,cos30°),
∴OA= = ,
∵圆的半径为2,
∴OA<2,
∴点A在圆内,
∴直线和圆一定相交,
故答案为:A.
分析:设圆心到直线的距离为d,圆的半径为r,直线与圆的位置关系有三种;当dr,直线与圆相离;当dr,直线与圆相切;当dr,直线与圆相交。根据已知条件求出直线经过的点与圆心的距离d,再将距离d与半径r比较大小即可判断选项A符合题意。
6.答案:B
解析:解:圆的半径是 ×12=6(cm),
则圆心到直线l的距离等于半径,则直线l与⊙O相切.
故选B.
分析:比较圆的半径和圆心到直线的距离的大小即可判断.
7.答案:D
解析:解:∵△APO≌△BPO(HL),
∴∠AOP=∠BOP.
∵sin∠AOP=AP:OP=2:4=:2,
∴∠AOP=60°.
∴∠AOB=120°.
故选D.
分析:由切线长定理知△APO≌△BPO,得∠AOP=∠BOP.可求得sin∠AOP=:2,所以可知∠AOP=60°,从而求得∠AOB的值.
8.答案:B
解析:连接DO,
∵BC是⊙O的直径,AD是⊙O的切线,切点为D,
∴∠BDC=∠ADO=90°,
∵DO=CO,
∴∠C=∠CDO=30°,
∴∠A=30°,∠DBC=60°,
∠ADB=30°,
∴AD=DC,故①正确;
∵∠A=30°,∠DBC=60°,
∴∠ADB=30°,
∴AB=BD,故②正确;
∵∠C=30°,∠BDC=90°,
∴BD= BC,
∵AB=BD,
∴AB= BC,故③正确;
无法得到BD=CD,故④错误.
故答案为:B.
分析:连接DO,①由直径所对的圆周角是直角和圆的切线的性质可得∠BDC=∠ADO=90°,结合已知易求得∠A=∠C=30°,所以AD=DC;②由① 的计算可得∠A=30°,∠AOD=60°,由三角形外角的性质可求得∠ADB=∠A=30°,所以AB=BD;③在直角三角形BCD中,由30度角所对的直角边等于斜边的一半可得BD=BC,结合②的结论可得AB=BD=BC;④由前面的计算可得:∠C<∠CBD,由大角对大边可得CD﹥BD。
9.答案:A
解析:当AB与小圆相切,
∵大圆半径为5,小圆的半径为3,
∴AB=2 =8.
∵大圆的弦AB与小圆有公共点,即相切或相交,
∴8≤AB≤10.
故答案为:A.
分析:由题意可求得大圆的直径是10,当AB是大圆的直径时,与圆由两个公共点,且AB最长是10;当AB与小圆相切时,AB与小圆只有一个公共点,用勾股定理可求得此时AB的长是8,;综合这两种情况可求得AB的范围是8≤AB≤10.
10.答案:A
解析:作AD⊥BC于D.
根据等腰三角形的三线合一,得BD=4cm;
再根据勾股定理得AD=2 cm,
∵2 >4cm
∴以4cm为半径的⊙A与BC所在直线的位置关系是相离.
故答案为:A.
分析:作AD⊥BC于D,根据等腰三角形的三线合一可求得BD的值,再用勾股定理可求得AD的长;把圆心A到BC的距离AD与圆的半径4比较大小,根据直线和圆的位置关系:圆心到直线的距离大于半径时,直线和圆相离可求解。
11.答案:D
解析:解 :∵圆心(-3,4),∴圆心到x轴的距离为4,到y轴的距离为3,又∵该圆的半径为34,∴该圆心到x轴的距离等于该圆的半径,到y轴的距离小于该圆的半径,∴此圆与x轴相切,与y轴相交。
故答案为:D
分析:由题可知圆心(-3,4)到x轴的距离为4,到y轴的距离为3,而圆的半径为4,则此圆与x轴相切,与y轴相交。
12.答案:D
解析:解: 如图,
直线y= x+2 与x轴交于点C,与y轴交于点D,作OH⊥CD于H,
当x=0时,y= x+2 =2 ,则D(0,2 ),
当y=0时, x+2 =0,解得x=﹣2,则C(﹣2,0),
∴CD= =4,
∵ OH CD= OC OD,
∴OH= = ,
连接OA,如图,
∵PA为⊙O的切线,
∴OA⊥PA,
∴PA= = ,
当OP的值最小时,PA的值最小,
而OP的最小值为OH的长,
∴PA的最小值为 = .
故答案为:D.
分析:作OH⊥CD于H,先利用一次函数解析式得到D、C的坐标,再利用勾股定理可计算出CD=4,则利用面积法可计算出OH,连接OA,利用切线的性质得出用含OP的代数式表示PA,利用垂线段最短求PA的最小值.
13.答案:相离
解析:解:∴⊙O的半径为4cm,如果圆心O到直线l的距离为5cm,
∴5>4,
即d>r,
∴直线l与⊙O的位置关系是相离,
故答案为:相离.
分析:设圆心O到直线l的距离为d,⊙O的半径为r,如果dr,那么直线与圆相离。根据题意知d>r,所以直线l与⊙O的位置关系是相离。
14.答案:⊙O上;外;内
解析:因为直径是8cm,则半径是4cm。OM=4cm,所以M点在⊙O上;ON=8cm,所以N点在⊙O外;OP=2cm,所以P点在⊙O内。
分析:在点与圆的位置关系判定中,点与圆心的距离大于半径的,该点在圆外;点与圆心的距离等于半径的,该点在圆上;点与圆心的距离大小于半径的,该点在圆内。本题需要依据该普安段方法进行解题。
15.答案:125
解析:连接OD,则∠ODC=90°,∠COD=70°;
∵OA=OD,
∴∠ODA=∠A= ∠COD=35°,
∴∠CDA=∠CDO+∠ODA=90°+35°=125°,
故答案为:125.
分析:连接OD,由圆的切线的性质可得∠ODC=90°,由三角形外角的性质可得∠BOD=∠A+∠ADO,而∠A=∠ADO,所以∠ADO的度数可求解,则∠CDA=∠ODC+∠ADO可求解。
16.答案: 或
解析:解:如图1中,当⊙P与直线AC相切于点Q时,连接PQ.
设PQ=PA′=r,
∵PQ∥CA′,
∴ = ,
∴ = ,
∴r= .
如图2中,当⊙P与AB相切于点T时,易证A′、B′、T共线,
∵△A′BT∽△ABC,
∴ = ,
∴ = ,
∴A′T= ,
∴r= A′T= .
综上所述,⊙P的半径为 或 .
分析:如图1中,当⊙P与直线AC相切于点Q时,连接PQ.根据平行线分线段成比例定理得出=根据比例式建立方程即可算出该圆的半径;如图2中,当⊙P与AB相切于点T时,易证A′、B′、T共线,首先证出△A′BT∽△ABC,根据相似三角形对应边成比例得出=,根据比例式即可算出A′T的长,进而求出该圆的半径,综上所述即可得出答案。
17.答案:3<r≤4或r=2.4
解析:解:如图,∵BC>AC,
∴以C为圆心,r为半径所作的圆与斜边AB只有一个公共点.
根据勾股定理求得AB=5.
分两种情况:
①圆与AB相切时,即r=CD=3×4÷5=2.4;
②点A在圆内部,点B在圆上或圆外时,此时AC<r≤BC,即3<r≤4.
∴3<r≤4或r=2.4.
分析:根据勾股定理算出AB的长,利用三角形的面积法算出CD的长,然后分①圆与AB相切时,此时r=CD,②点A在圆内部,点B在圆上或圆外时,此时AC<r≤BC,即3<r≤4,综上所述即可得出答案。
18.答案:解:过点C作CD⊥AB于点D
∵Rt△ABC中,CA=6,CB=8,
∴AB=
∵S△ABC=ABCD=ACBC
∴10CD=6×8
解之:CD=
∴当CD=r=时,⊙C与AB相切
故答案为:r=
解析:过点C作CD⊥AB于点D,利用勾股定理求出AB的长,再利用面积法求出CD的长,要使⊙C与AB相切,则CD=r,即可解答。
19.答案:解:如图,过点O作OM⊥AC于点M,ON⊥AB于点N,
∵OM⊥AC,
∴AM=AC=,
在Rt△AMO中,OM=
∴与AC相切的圆的半径为1cm;
∵ON⊥AB,
∴AN=AB=×4=2
在Rt△ANO中,ON=
∵>1,
∴这个圆与直线AB相离。
解析:过点O作OM⊥AC于点M,ON⊥AB于点N,利用垂径定理分别求出AM、AN的长,再利用勾股定理分别求出OM、ON的长,根据直线与圆相切,则ON=r,根据d>r,直线与圆相离,可得出答案。
20.答案:证明:连接OE
∵OE=OA
∴∠1=∠OEA
∵BC是圆O的切线
∴OE⊥BC
∵∠B=90°
∴AB⊥BC
∴OE∥AB
∴∠OEA=∠BAE
∴∠1=∠BAE
∴AE平分∠CAB。
解析:利用切线的性质可得出OE⊥BC,再由已知Rt△ABC,去证明OE∥AB,由平行线的性质及等腰三角形的性质,再证明∠OEA=∠BAE,∠1=∠OEA,就可证得结论。
21.答案:解:根据题意画出图形,
根据题意可知AB=60千米,∠BAF=30°
过B作BD⊥AF于点D,作BE=BF=50千米,分别交AF于点E、F
∵ BD⊥AF,AB=60千米,∠BAF=30°
∴ 风暴离B城市的最近距离为BD=AB×sin30°=30千米,
∵ BD<50千米
∴ 沿海城市B会受到这次风暴的影响
∵ BE=BF=50千米
∴ 沿海城市B受影响时风暴所走的路程为线段EF
∵ BE=BF=50千米,BD=30千米,BD⊥AF
∴ DF=DE=
∴ EF=2DF=80千米
∵ 风暴速度为每小时20千米
∴ 受影响时间==4小时
∴沿海城市B会受到这次风暴的影响,受影响的时间为4小时。
解析:根据题意画出图形,则AB=60千米,∠BAF=30°,将实际问题转化为直角三角形的问题.过B作BD⊥AF交AF于点D,作BE=BF=50千米,分别交AF于点E、F,要判断B点是否受影响,就要求出点B到风暴路线的最短距离BD,若BD≤50千米,则受影响,否则不受影响,利用解直角三角形求出BD的长,由BD<50千米可得沿海城市B会受到这次风暴的影响,然后利用勾股定理求出DF的长,就可得出EF的长,继而可求出沿海城市B会受到这次风暴的影响,受影响的时间。
22.答案:解:发现:如图2,设半圆K与PC交点为R,连接RK,过点P作PH⊥AD于点H,过点R作RE⊥KQ于点E,在Rt△OPH中,PH=AB=1,OP=2,∴∠POH=30°,∴α=60°﹣30°=30°,∵AD∥BC,∴∠RPO=∠POH=30°,∴∠RKQ=2×30°=60°,∴S扇形KRQ= = ,在Rt△RKE中,RE=RK sin60°= ,∴S△PRK= RE= ,∴S阴影= + ;拓展:如图5, ∵∠OAN=∠MBN=90°,∠ANO=∠BNM,∴△AON∽△BMN,∴ ,即 ,∴BN= ,如图4,当点Q落在BC上时,x取最大值,作QF⊥AD于点F,BQ=AF= ﹣AO=2 ﹣1,∴x的取值范围是0<x≤2 ﹣1;探究:半圆K与矩形ABCD的边相切,分三种情况;①如图5,半圆K与BC相切于点T,设直线KT与AD,OQ的初始位置所在的直线分别交于点S,O′,则∠KSO=∠KTB=90°,作KG⊥OO′于G,在Rt△OSK中,OS= =2,在Rt△OSO′中,SO′=OS tan60°=2 ,KO′=2 ﹣ ,在Rt△KGO′中,∠O′=30°,∴KG= KO′= ﹣ ,∴在Rt△OGK中,sinα= = = ,②当半圆K与AD相切于T,如图6,同理可得sinα= = = = ;③当半圆K与CD切线时,点Q与点D重合,且为切点,∴α=60°,∴sinα=sin60°= ;综上所述sinα的值为: 或 或
解析:首先设半圆K与PC交点为R,连接RK,过点P作PH⊥AD于点H,过点R作RE⊥KQ于点E,根据直角三角形的直角边与斜边的关系得出∠POH=30° ;进而求得α的度数,根据平行线的性质及圆周角定理得出∠RKQ的度数,然后利用S阴影=S扇形KRQ+S△PRK求得答案;
拓展:如图5,由∠OAN=∠MBN=90°,∠ANO=∠BNM,得到△AON∽△BMN,根据相似三角形对应边成比例即可求得BN,如图4,当点Q落在BC上时,x取最大值,作QF⊥AD于点F,根据勾股定理求出BQ=AF的值,则可求出x的取值范围;
探究:半圆K与矩形ABCD的边相切,分三种情况:①半圆K与BC相切于点T,②当半圆K与AD相切于T,③当半圆K与CD切线时,点Q与点D重合,且为切点;分别求解即可求得答案.
将来的某一天,你会感谢曾经努力的自己!
3.6直线与圆的位置关系 同步练习
姓名: 班级:
一、选择题
1.若直线l与☉O有公共点,则直线l与☉O的位置关系可能是( )
A.相交或相切 B.相交或相离 C.相切或相离 D.无法确定
2.已知⊙O的半径为6cm,圆心O到直线l的距离为5cm,则直线l与⊙O的交点个数为( )
A.0 B.l C.2 D.无法确定
3.已知在平面直角坐标系中,圆P的圆心坐标为(4,5),半径为3个单位长度,把圆P沿水平方向向左平移d个单位长度后恰好与y轴相切,则d的值是( )
A.1 B.2 C.2或8 D.1或7
4.如图,点P为⊙O外一点,PA为⊙O的切线,A为切点,PO交⊙O于点B,∠P=30°,OB=3,则线段BP的长为( )
A.3 B.3 C.6 D.9
5.在平面直角坐标系xOy中,经过点(sin45°,cos30°)的直线,与以原点为圆心,2为半径的圆的位置关系是( )
A.相交 B.相切
C.相离 D.以上三者都有可能
6.已知⊙O的直径为12cm,圆心到直线l的距离为6cm,则直线l与⊙O的位置关系是( )
A.相离 B.相切 C.相交 D.无法确定
7.如图,PA、PB是⊙O的两条切线,切点是A、B.如果OP=4,PA=2,那么∠AOB等于( )
A.90° B.100° C.110° D.120°
8.如图,BC是⊙O的直径,AD是⊙O的切线,切点为D,AD与CB的延长线交于点A,∠C=30°,给出下面四个结论:
①AD=DC;②AB=BD;③AB= BC;④BD=CD,
其中正确的个数为( )
A.4个 B.3个 C.2个 D.1个
9.如图,两个同心圆,大圆的半径为5,小圆的半径为3,若大圆的弦AB与小圆有公共点,则弦AB的取值范围是( )
A.8≤AB≤10 B.8<AB≤10 C.4≤AB≤5 D.4<AB≤5
10.已知△ABC中,AB=AC=6cm,BC=8cm,以点A为圆心,以4cm长为半径作圆,则⊙A与BC的位置关系是( )
A.相离 B.相切 C.相交 D.外离
11.在平面直角坐标系中,以点(-3,4)为圆心,4为半径的圆( )
A.与x轴相交,与y轴相切 B.与x轴相离,与y轴相交
C.与x轴相切,与y轴相离 D.与x轴相切,与y轴相交
12.在平面直角坐标系内,以原点O为圆心,1为半径作圆,点P在直线y= 上运动,过点P作该圆的一条切线,切点为A,则PA的最小值为( )
A.3 B.2 C. D.
二、填空题
13.若⊙O的半径为4cm,圆心O到直线l的距离为5cm,则直线l与⊙O的位置关系是 .
14.⊙O直径为8cm,有M、N、P三点,OM=4cm,ON=8cm,OP=2cm,则M点在 ,N点在圆 ,P点在圆 。
15.如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,若∠C=20°,则∠CDA= °.
16.如图,△ABC中,∠ACB=90°,sinA= ,AC=12,将△ABC绕点C顺时针旋转90°得到△A'B'C,P为线段A′B'上的动点,以点P为圆心,PA′长为半径作⊙P,当⊙P与△ABC的边相切时,⊙P的半径为 .
在Rt△ABC中,∠C=90°,AC=3,BC=4.若以C点为圆心,r为半径所作的圆与斜边AB只有一个公共点,则r的取值范围是 .
三、解答题
18.如图所示,Rt△ABC中,∠ACB=90°,CA=6,CB=8,以C为圆心,r为半径作⊙C,当r为多少时,⊙C与AB相切?
19.如图,⊙O的半径为3cm,弦AC=4 cm,AB=4cm,若以O为圆心,再作一个圆与AC相切,则这个圆的半径为多少?这个圆与AB的位置关系如何?
20.如图,已知点O为Rt△ABC斜边AC上一点,以点O为圆心,OA长为半径的⊙O与BC相切于点E,与AC相交于点D,连接AE.
求证:AE平分∠CAB;
在南部沿海某气象站A测得一热带风暴从A的南偏东30°的方向迎着气象站袭来,已知该风暴速度为每小时20千米,风暴周围50千米范围内将受到影响,若该风暴不改变速度与方向,问气象站正南方60千米处的沿海城市B是否会受这次风暴的影响?若不受影响,请说明理由;若受影响,请求出受影响的时间.
22.平面上,矩形ABCD与直径为QP的半圆K如图1摆放,分别延长DA和QP交于点O,且∠DOQ=60°,OQ=OD=3,OP=2,OA=AB=1.让线段OD及矩形ABCD位置固定,将线段OQ连带着半圆K一起绕着点O按逆时针方向开始旋转,设旋转角为α(0°≤α≤60°).
发现:如图2,当点P恰好落在BC边上时,求a的值即阴影部分的面积;
拓展:如图3,当线段OQ与CB边交于点M,与BA边交于点N时,设BM=x(x>0),用含x的代数式表示BN的长,并求x的取值范围.
探究:当半圆K与矩形ABCD的边相切时,直接写出sinα的值.
答案解析部分
1.答案:A
解析:解 :①一个公共点,直线与圆相切,②两个公共点,直线与圆相交。
故答案为:相交或相切。
分析:分直线与圆公共点的个数来讨论:①一个公共点,直线与圆相切,②两个公共点,直线与圆相交。
2.答案:C
解析:∵⊙O的半径为6cm,圆心O到直线l的距离为5cm,6cm>5cm,
∴直线l与⊙O相交,
∴直线l与⊙O有两个交点.
故答案为:C.
分析:直线和圆的位置关系是:圆心到直线的距离小于半径时,直线与圆相交,直线与圆有两个公共点,所以由题意可得直线l与圆相交,于是可知;直线l与⊙O有两个交点。
3.答案:D
解析:当⊙p在原点右侧与y轴相切时,x-d=r,
∴d=x-r=1.
当⊙p在原点左侧与y轴相切时,
x+r=d,
∴d=7,
所以d的值是1或7.
故答案为:D.
分析:由题意可知:圆P平移前在y轴的右侧,所以有两种情况:
①当⊙p在原点右侧与y轴相切时,根据直线和圆的位置关系,当圆心P到直线的距离等于半径时,直线和圆相切,可求解;
②当⊙p在原点左侧与y轴相切时,同理可求解。综合两种情况可判断选项。
4.答案:A
解析:解:连接OA,
∵PA为⊙O的切线,
∴∠OAP=90°,
∵∠P=30°,OB=3,
∴AO=3,则OP=6,
故BP=6﹣3=3.
故答案为:A.
分析:连接OA,根据切线垂直于经过切点的半径得出∠OAP=90°,根据含30°直角三角形的边之间的关系得出OP的长,最后根据BP=OP-OB即可算出答案。
5.答案:A
解析:解:设直线经过的点为A,
∵点A的坐标为(sin45°,cos30°),
∴OA= = ,
∵圆的半径为2,
∴OA<2,
∴点A在圆内,
∴直线和圆一定相交,
故答案为:A.
分析:设圆心到直线的距离为d,圆的半径为r,直线与圆的位置关系有三种;当dr,直线与圆相离;当dr,直线与圆相切;当dr,直线与圆相交。根据已知条件求出直线经过的点与圆心的距离d,再将距离d与半径r比较大小即可判断选项A符合题意。
6.答案:B
解析:解:圆的半径是 ×12=6(cm),
则圆心到直线l的距离等于半径,则直线l与⊙O相切.
故选B.
分析:比较圆的半径和圆心到直线的距离的大小即可判断.
7.答案:D
解析:解:∵△APO≌△BPO(HL),
∴∠AOP=∠BOP.
∵sin∠AOP=AP:OP=2:4=:2,
∴∠AOP=60°.
∴∠AOB=120°.
故选D.
分析:由切线长定理知△APO≌△BPO,得∠AOP=∠BOP.可求得sin∠AOP=:2,所以可知∠AOP=60°,从而求得∠AOB的值.
8.答案:B
解析:连接DO,
∵BC是⊙O的直径,AD是⊙O的切线,切点为D,
∴∠BDC=∠ADO=90°,
∵DO=CO,
∴∠C=∠CDO=30°,
∴∠A=30°,∠DBC=60°,
∠ADB=30°,
∴AD=DC,故①正确;
∵∠A=30°,∠DBC=60°,
∴∠ADB=30°,
∴AB=BD,故②正确;
∵∠C=30°,∠BDC=90°,
∴BD= BC,
∵AB=BD,
∴AB= BC,故③正确;
无法得到BD=CD,故④错误.
故答案为:B.
分析:连接DO,①由直径所对的圆周角是直角和圆的切线的性质可得∠BDC=∠ADO=90°,结合已知易求得∠A=∠C=30°,所以AD=DC;②由① 的计算可得∠A=30°,∠AOD=60°,由三角形外角的性质可求得∠ADB=∠A=30°,所以AB=BD;③在直角三角形BCD中,由30度角所对的直角边等于斜边的一半可得BD=BC,结合②的结论可得AB=BD=BC;④由前面的计算可得:∠C<∠CBD,由大角对大边可得CD﹥BD。
9.答案:A
解析:当AB与小圆相切,
∵大圆半径为5,小圆的半径为3,
∴AB=2 =8.
∵大圆的弦AB与小圆有公共点,即相切或相交,
∴8≤AB≤10.
故答案为:A.
分析:由题意可求得大圆的直径是10,当AB是大圆的直径时,与圆由两个公共点,且AB最长是10;当AB与小圆相切时,AB与小圆只有一个公共点,用勾股定理可求得此时AB的长是8,;综合这两种情况可求得AB的范围是8≤AB≤10.
10.答案:A
解析:作AD⊥BC于D.
根据等腰三角形的三线合一,得BD=4cm;
再根据勾股定理得AD=2 cm,
∵2 >4cm
∴以4cm为半径的⊙A与BC所在直线的位置关系是相离.
故答案为:A.
分析:作AD⊥BC于D,根据等腰三角形的三线合一可求得BD的值,再用勾股定理可求得AD的长;把圆心A到BC的距离AD与圆的半径4比较大小,根据直线和圆的位置关系:圆心到直线的距离大于半径时,直线和圆相离可求解。
11.答案:D
解析:解 :∵圆心(-3,4),∴圆心到x轴的距离为4,到y轴的距离为3,又∵该圆的半径为34,∴该圆心到x轴的距离等于该圆的半径,到y轴的距离小于该圆的半径,∴此圆与x轴相切,与y轴相交。
故答案为:D
分析:由题可知圆心(-3,4)到x轴的距离为4,到y轴的距离为3,而圆的半径为4,则此圆与x轴相切,与y轴相交。
12.答案:D
解析:解: 如图,
直线y= x+2 与x轴交于点C,与y轴交于点D,作OH⊥CD于H,
当x=0时,y= x+2 =2 ,则D(0,2 ),
当y=0时, x+2 =0,解得x=﹣2,则C(﹣2,0),
∴CD= =4,
∵ OH CD= OC OD,
∴OH= = ,
连接OA,如图,
∵PA为⊙O的切线,
∴OA⊥PA,
∴PA= = ,
当OP的值最小时,PA的值最小,
而OP的最小值为OH的长,
∴PA的最小值为 = .
故答案为:D.
分析:作OH⊥CD于H,先利用一次函数解析式得到D、C的坐标,再利用勾股定理可计算出CD=4,则利用面积法可计算出OH,连接OA,利用切线的性质得出用含OP的代数式表示PA,利用垂线段最短求PA的最小值.
13.答案:相离
解析:解:∴⊙O的半径为4cm,如果圆心O到直线l的距离为5cm,
∴5>4,
即d>r,
∴直线l与⊙O的位置关系是相离,
故答案为:相离.
分析:设圆心O到直线l的距离为d,⊙O的半径为r,如果dr,那么直线与圆相离。根据题意知d>r,所以直线l与⊙O的位置关系是相离。
14.答案:⊙O上;外;内
解析:因为直径是8cm,则半径是4cm。OM=4cm,所以M点在⊙O上;ON=8cm,所以N点在⊙O外;OP=2cm,所以P点在⊙O内。
分析:在点与圆的位置关系判定中,点与圆心的距离大于半径的,该点在圆外;点与圆心的距离等于半径的,该点在圆上;点与圆心的距离大小于半径的,该点在圆内。本题需要依据该普安段方法进行解题。
15.答案:125
解析:连接OD,则∠ODC=90°,∠COD=70°;
∵OA=OD,
∴∠ODA=∠A= ∠COD=35°,
∴∠CDA=∠CDO+∠ODA=90°+35°=125°,
故答案为:125.
分析:连接OD,由圆的切线的性质可得∠ODC=90°,由三角形外角的性质可得∠BOD=∠A+∠ADO,而∠A=∠ADO,所以∠ADO的度数可求解,则∠CDA=∠ODC+∠ADO可求解。
16.答案: 或
解析:解:如图1中,当⊙P与直线AC相切于点Q时,连接PQ.
设PQ=PA′=r,
∵PQ∥CA′,
∴ = ,
∴ = ,
∴r= .
如图2中,当⊙P与AB相切于点T时,易证A′、B′、T共线,
∵△A′BT∽△ABC,
∴ = ,
∴ = ,
∴A′T= ,
∴r= A′T= .
综上所述,⊙P的半径为 或 .
分析:如图1中,当⊙P与直线AC相切于点Q时,连接PQ.根据平行线分线段成比例定理得出=根据比例式建立方程即可算出该圆的半径;如图2中,当⊙P与AB相切于点T时,易证A′、B′、T共线,首先证出△A′BT∽△ABC,根据相似三角形对应边成比例得出=,根据比例式即可算出A′T的长,进而求出该圆的半径,综上所述即可得出答案。
17.答案:3<r≤4或r=2.4
解析:解:如图,∵BC>AC,
∴以C为圆心,r为半径所作的圆与斜边AB只有一个公共点.
根据勾股定理求得AB=5.
分两种情况:
①圆与AB相切时,即r=CD=3×4÷5=2.4;
②点A在圆内部,点B在圆上或圆外时,此时AC<r≤BC,即3<r≤4.
∴3<r≤4或r=2.4.
分析:根据勾股定理算出AB的长,利用三角形的面积法算出CD的长,然后分①圆与AB相切时,此时r=CD,②点A在圆内部,点B在圆上或圆外时,此时AC<r≤BC,即3<r≤4,综上所述即可得出答案。
18.答案:解:过点C作CD⊥AB于点D
∵Rt△ABC中,CA=6,CB=8,
∴AB=
∵S△ABC=ABCD=ACBC
∴10CD=6×8
解之:CD=
∴当CD=r=时,⊙C与AB相切
故答案为:r=
解析:过点C作CD⊥AB于点D,利用勾股定理求出AB的长,再利用面积法求出CD的长,要使⊙C与AB相切,则CD=r,即可解答。
19.答案:解:如图,过点O作OM⊥AC于点M,ON⊥AB于点N,
∵OM⊥AC,
∴AM=AC=,
在Rt△AMO中,OM=
∴与AC相切的圆的半径为1cm;
∵ON⊥AB,
∴AN=AB=×4=2
在Rt△ANO中,ON=
∵>1,
∴这个圆与直线AB相离。
解析:过点O作OM⊥AC于点M,ON⊥AB于点N,利用垂径定理分别求出AM、AN的长,再利用勾股定理分别求出OM、ON的长,根据直线与圆相切,则ON=r,根据d>r,直线与圆相离,可得出答案。
20.答案:证明:连接OE
∵OE=OA
∴∠1=∠OEA
∵BC是圆O的切线
∴OE⊥BC
∵∠B=90°
∴AB⊥BC
∴OE∥AB
∴∠OEA=∠BAE
∴∠1=∠BAE
∴AE平分∠CAB。
解析:利用切线的性质可得出OE⊥BC,再由已知Rt△ABC,去证明OE∥AB,由平行线的性质及等腰三角形的性质,再证明∠OEA=∠BAE,∠1=∠OEA,就可证得结论。
21.答案:解:根据题意画出图形,
根据题意可知AB=60千米,∠BAF=30°
过B作BD⊥AF于点D,作BE=BF=50千米,分别交AF于点E、F
∵ BD⊥AF,AB=60千米,∠BAF=30°
∴ 风暴离B城市的最近距离为BD=AB×sin30°=30千米,
∵ BD<50千米
∴ 沿海城市B会受到这次风暴的影响
∵ BE=BF=50千米
∴ 沿海城市B受影响时风暴所走的路程为线段EF
∵ BE=BF=50千米,BD=30千米,BD⊥AF
∴ DF=DE=
∴ EF=2DF=80千米
∵ 风暴速度为每小时20千米
∴ 受影响时间==4小时
∴沿海城市B会受到这次风暴的影响,受影响的时间为4小时。
解析:根据题意画出图形,则AB=60千米,∠BAF=30°,将实际问题转化为直角三角形的问题.过B作BD⊥AF交AF于点D,作BE=BF=50千米,分别交AF于点E、F,要判断B点是否受影响,就要求出点B到风暴路线的最短距离BD,若BD≤50千米,则受影响,否则不受影响,利用解直角三角形求出BD的长,由BD<50千米可得沿海城市B会受到这次风暴的影响,然后利用勾股定理求出DF的长,就可得出EF的长,继而可求出沿海城市B会受到这次风暴的影响,受影响的时间。
22.答案:解:发现:如图2,设半圆K与PC交点为R,连接RK,过点P作PH⊥AD于点H,过点R作RE⊥KQ于点E,在Rt△OPH中,PH=AB=1,OP=2,∴∠POH=30°,∴α=60°﹣30°=30°,∵AD∥BC,∴∠RPO=∠POH=30°,∴∠RKQ=2×30°=60°,∴S扇形KRQ= = ,在Rt△RKE中,RE=RK sin60°= ,∴S△PRK= RE= ,∴S阴影= + ;拓展:如图5, ∵∠OAN=∠MBN=90°,∠ANO=∠BNM,∴△AON∽△BMN,∴ ,即 ,∴BN= ,如图4,当点Q落在BC上时,x取最大值,作QF⊥AD于点F,BQ=AF= ﹣AO=2 ﹣1,∴x的取值范围是0<x≤2 ﹣1;探究:半圆K与矩形ABCD的边相切,分三种情况;①如图5,半圆K与BC相切于点T,设直线KT与AD,OQ的初始位置所在的直线分别交于点S,O′,则∠KSO=∠KTB=90°,作KG⊥OO′于G,在Rt△OSK中,OS= =2,在Rt△OSO′中,SO′=OS tan60°=2 ,KO′=2 ﹣ ,在Rt△KGO′中,∠O′=30°,∴KG= KO′= ﹣ ,∴在Rt△OGK中,sinα= = = ,②当半圆K与AD相切于T,如图6,同理可得sinα= = = = ;③当半圆K与CD切线时,点Q与点D重合,且为切点,∴α=60°,∴sinα=sin60°= ;综上所述sinα的值为: 或 或
解析:首先设半圆K与PC交点为R,连接RK,过点P作PH⊥AD于点H,过点R作RE⊥KQ于点E,根据直角三角形的直角边与斜边的关系得出∠POH=30° ;进而求得α的度数,根据平行线的性质及圆周角定理得出∠RKQ的度数,然后利用S阴影=S扇形KRQ+S△PRK求得答案;
拓展:如图5,由∠OAN=∠MBN=90°,∠ANO=∠BNM,得到△AON∽△BMN,根据相似三角形对应边成比例即可求得BN,如图4,当点Q落在BC上时,x取最大值,作QF⊥AD于点F,根据勾股定理求出BQ=AF的值,则可求出x的取值范围;
探究:半圆K与矩形ABCD的边相切,分三种情况:①半圆K与BC相切于点T,②当半圆K与AD相切于T,③当半圆K与CD切线时,点Q与点D重合,且为切点;分别求解即可求得答案.
将来的某一天,你会感谢曾经努力的自己!
