2023-2024学年北师大版九年级下册3.1圆 同步练习(含解析)
文档属性
| 名称 | 2023-2024学年北师大版九年级下册3.1圆 同步练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 459.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-19 16:42:58 | ||
图片预览




文档简介
2023-2024学年北师大版九年级下册同步练习【提升卷】
3.1圆 同步练习
班级: 姓名:
一、选择题
1.下列命题中,正确的是( )
A.圆只有一条对称轴
B.圆的对称轴不止一条,但只有有限条
C.圆有无数条对称轴,每条直径都是它的对称轴
D.圆有无数条对称轴,经过圆心的每条直线都是它的对称轴
2.车轮要做成圆形,实际上就是根据圆的特征( )
A.同弧所对的圆周角相等 B.直径是圆中最大的弦
C.圆上各点到圆心的距离相等 D.圆是中心对称图形
3.由所有到已知点O的距离大于或等于3,并且小于或等于5的点组成的图形的面积为( )
A.4π B.9π C.16π D.25π
4.如图,在⊙O中,点B,O,C和点A,O,D分别在同一条直线上,则图中有( )条弦
A.2 B.3 C.4 D. 5
5.下列说法,正确的是( )
A.半径相等的两个圆大小相等 B.长度相等的两条弧是等弧
C.直径不一定是圆中最长的弦 D.圆上两点之间的部分叫做弦
6.Rt△ABC中,∠C=90°,AC=2,BC=4,如果以点A为圆心,AC为半径作⊙A,那么斜边中点D与⊙A的位置关系是( )
A.点D在⊙A外 B.点D在⊙A上 C.点D在⊙A内 D.无法确定
7.如图,AB是⊙O的直径,点C,D在⊙O上,且点C、D在AB的异侧,连结AD,OD,OC.若∠AOC=70°,且AD∥OC,则∠AOD的度数为( )
A.70° B.60° C.50° D.40°
8.如图,以坐标原点O为圆心的圆与y轴交于点A、B,且OA=1,则点B的坐标是( )
A.(0,1) B.(0,﹣1) C.( 1,0) D.(﹣1,0)
9.在△ABC中,若O为BC边的中点,则必有:AB2+AC2=2AO2+2BO2成立.依据以上结论,解决如下问题:如图,在矩形DEFG中,已知DE=4,EF=3,点P在以DE为直径的半圆上运动,则PF2+PG2的最小值为( )
A. B. C.34 D.10
10.在数轴上,点A所表示的实数为3,点B所表示的实数为a,⊙A的半径为2.那么下列说法中不正确的是( )
A.当a<1时,点B在⊙A外 B.当1<a<5时,点B在⊙A内
C.当a<5时,点B在⊙A内 D.当a>5时,点B在⊙A外
11.(2022九上·沭阳月考)一个点到圆的最大距离为11cm,最小距离为5cm,则圆的半径为( )
A.16cm或6cm, B.3cm或8cm C.3cm D.8cm
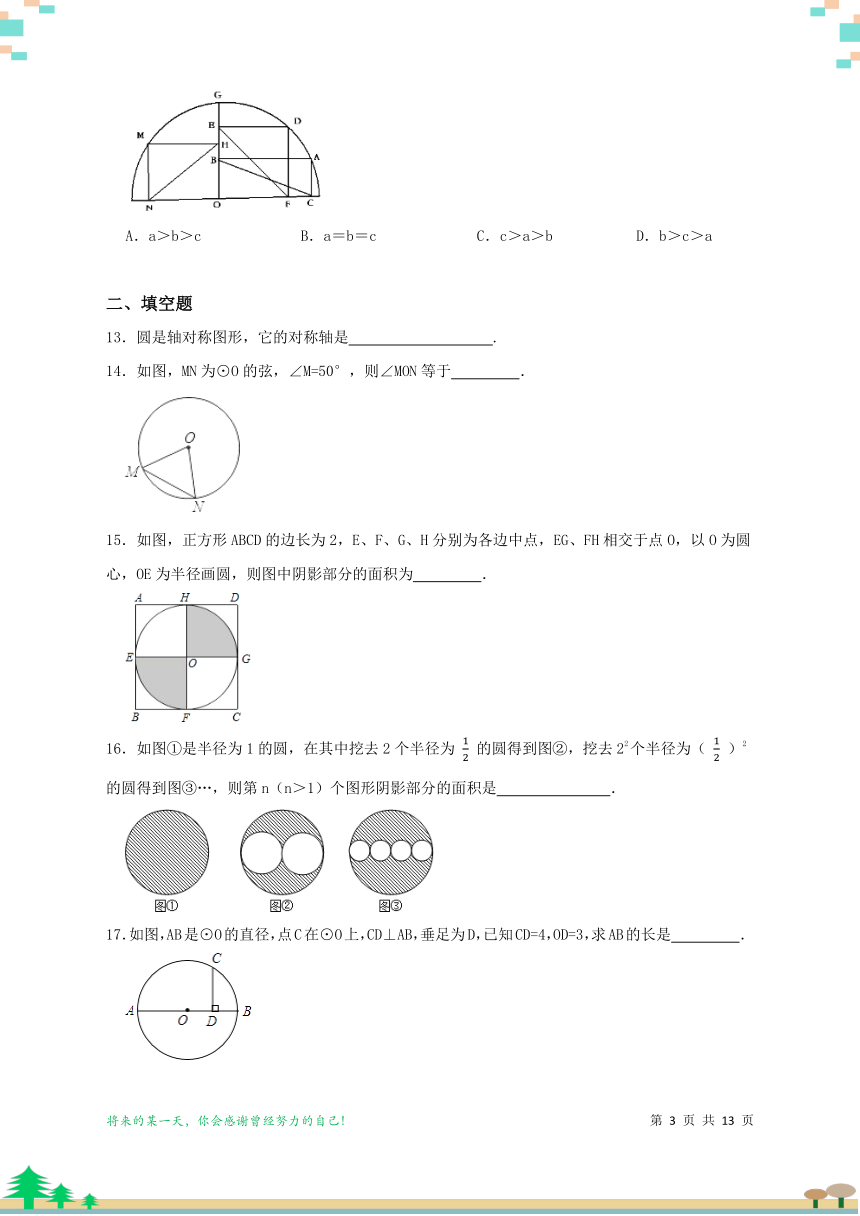
12.如图点A,D,G,B在半圆上,四边形ABOC,DEOF,HMNO均为矩形,设BC=a, EF=b, NH=c,则下列说法正确的是( )
A.a>b>c B.a=b=c C.c>a>b D.b>c>a
二、填空题
13.圆是轴对称图形,它的对称轴是 .
14.如图,MN为⊙O的弦,∠M=50°,则∠MON等于 .
15.如图,正方形ABCD的边长为2,E、F、G、H分别为各边中点,EG、FH相交于点O,以O为圆心,OE为半径画圆,则图中阴影部分的面积为 .
16.如图①是半径为1的圆,在其中挖去2个半径为 的圆得到图②,挖去22个半径为( )2的圆得到图③…,则第n(n>1)个图形阴影部分的面积是 .
17.如图,AB是⊙O的直径,点C在⊙O上,CD⊥AB,垂足为D,已知CD=4,OD=3,求AB的长是 .
三、解答题
18.已知:如图,在⊙O中,AB为弦,C、D两点在AB上,且AC=BD.
求证:△OAC≌△OBD.
19.如图,CD是⊙O的直径,E是⊙O上一点,∠EOD=48°,A为DC延长线上一点,且AB=OC,求∠A的度数.
20.如图,在Rt△ABC中,∠ACB=90°,AC=BC=2,以BC为直径的半圆交AB于D,P是 上的一个动点,连接AP,求AP的最小值.
21.如图,AB、CD为⊙O中两条直径,点E、F在直径CD上,且CE=DF.
求证:AF=BE.
22.如图,直线l经过⊙O的圆心O,且与⊙O交于A、B两点,点C在⊙O上,且∠AOC=30°,点P是直线l上的一个动点(与圆心O不重合),直线CP与⊙O相交于点Q.是否存在点P,使得QP=QO;若存在,求出相应的∠OCP的大小;若不存在,请简要说明理由.
答案解析部分
1.答案:D
解析:解:根据圆的性质和轴对称图形的定义可知:圆有无数条对称轴,每条直径所在的直线都是它的对称轴,由此可知D正确.
故答案为:D.
分析:轴对称图形:如果一个平面图形沿着一条直线折叠后,直线两旁的部分能够互相重合,这条直线叫做对称轴;根据圆的性质可知圆的对称轴是直径所在的直线.
2.答案:C
解析:根据圆的基本性质即可判断。
车轮要做成圆形,实际上就是根据圆上各点到圆心的距离相等,故选C.
【点评】本题属于基础应用题,只需学生熟练掌握圆的基本性质,即可完成。
3.答案:C
解析:解:由所有到已知点O的距离大于或等于3,并且小于或等于5的点组成的图形的面积是以5为半径的圆与以3为半径的圆组成的圆环的面积,
即π×52﹣π×32=16π,
故答案为:C.
分析:由所有到已知点O的距离大于或等于3,并且小于或等于5的点组成的图形的面积是以5为半径的圆与以3为半径的圆组成的圆环的面积,可得答案
4.答案:B
解析:圆中弦的定义:连接圆上任意两点的线段叫做弦。根据弦的定义可知,图中是弦的有:AB、BC、CE三条,则选项B符合题意。
故答案为:B
分析:首先要知道圆内弦的定义,其次利用弦定义解决问题。
5.答案:A
解析:A.根据半径确定圆的大小,故正确;
B.根据等弧的概念,长度相等的两条弧不一定能够重合,故错误;
C.根据三角形的两边之和大于第三边,可以证明直径是圆中最长的弦,故错误;
D.圆上任意两点间的部分叫弧,故错误.
故选A.
分析:理解等弧.直径.弦.弧的概念.
6.答案:A
【解析】解答:根据勾股定理求得斜边AB= =2 ,则AD= ,∵ >2,∴点在圆外.
故选A.
分析:本题根据点到圆心的距离和圆的半径之间的数量关系,来判断点和圆的位置关系.
7.答案:D
解析:解: ∵AD∥OC,
∴∠AOC=∠DAO=70°,
又∵OD=OA,
∴∠ADO=∠DAO=70°,
∴∠AOD=180﹣70°﹣70°=40°.
故答案为:D.
分析:根据平行线的性质,可求出∠DAO的度数,再根据等腰三角形的性质,可求得∠ODA的度数,然后利用三角形内角和定理求出∠AOD的度数。
8.答案:B
解析:解:∵以坐标原点O为圆心的圆与y轴交于点A、B,且OA=1,
∴点B的坐标是(0,﹣1).
故答案为:B
分析: 先根据同圆的半径相等得出OB=OA=1,再由点B在y轴的负半轴上即可求出点B的坐标.
9.答案:D
解析:解:设点M为DE的中点,点N为FG的中点,连接MN交半圆于点P,此时PN取最小值.
∵DE=4,四边形DEFG为矩形,
∴GF=DE,MN=EF,
∴MP=FN= DE=2,
∴NP=MN﹣MP=EF﹣MP=1,
∴PF2+PG2=2PN2+2FN2=2×12+2×22=10.
故答案为:D.
分析:设点M为DE的中点,点N为FG的中点,连接MN交半圆于点P,此时PN取最小值.根据矩形的性质得出GF=DE,MN=EF,根据同圆的半径相等得出MP=FN= DE=2,根据线段的和差,由NP=MN﹣MP=EF﹣MP得出NP的长,根据勾股定理及等式的性质即可由PF2+PG2=2PN2+2FN2算出答案。
10.答案:C
解析:解:A、a<1时,d>2,点B在⊙A外,故A正确;
B、当1<a<5时,点B在⊙A内,故B正确;
C、当1<a<5时,点B在⊙A内,故C错误;
D、当a>5时,点B在⊙A外,故D正确;
故选:C.
分析:根据当d>r时,点在圆外;当d=r时,点在圆上,当d<r时,点在圆内,可得答案.
11.答案:B
解析:若该点在圆外,则最大距离应该是过直径的线段,则直径=11-5=6cm,半径=cm,如图所示,
若该点在圆内,则最大距离应该是直径所包含的线段,则直径=11+5=16cm,半径=cm,如图所示,
分析:应该先分析出有几种情况,再利用点与圆的位置关系进行半径的计算。
12.答案:B
解析:由于四边形ABOC,DEOF,HMNO均为矩形,因此具有对角线相等的性质。连接OA、OD和OM,则OA=BC=a,OD=BF=b,OM=NH=c,又因为OA、OD和OM均为半径且相等,则a=b=c,B选项符合题意,故答案为:B。
分析:首先要将a、b、c转换为已知可求解的线段(本题为半径),最后利用圆的半径相等性质进行大小关系的比较。
13.答案:直径所在的直线
解析:解:依题可得:圆的对称轴是直径所在的直线.
故答案为:直径所在的直线.
分析:轴对称图形:一个图形沿一条直线折叠,直线两旁的部分能够完全重合的图形;这条直线叫做对称轴;结合圆的性质即可得出答案.
14.答案:80°
解析:解:∵OM=ON,
∴∠N=∠M=50°,
∴∠MON=180°﹣∠M﹣∠N=80°,
故答案为80°.
分析:利用等腰三角形的性质可得∠N的度数,根据三角形的内角和定理可得所求角的度数.
15.答案:
解析:解:由题意可得:OE=1,
阴影面积= = .
分析: 根据圆及正方形的对称性可知:图中阴影部分的半径其实质就是一个半圆的面积,根据半圆面积计算方法即可算出答案。
16.答案:(1﹣ )π
解析:解:图②中阴影部分的面积为:π×1
2﹣π×(
)
2×2=π﹣
π=(1﹣
)π=
π;
图③中阴影部分的面积为:π×12﹣π×[(
)2]2×22=π﹣
π=(1﹣
)π=
π;
图④是半径为1的圆,在其中挖去23个半径为(
)3的圆得到的,则图④中阴影部分的面积为:π×12﹣π×[(
)3]2×23=π﹣
π=(1﹣
)π=
π;
…,
则第n(n>1)个图形阴影部分的面积为:π×12﹣π×[(
)n﹣1]2×2n﹣1=π﹣
π=(1﹣
)π.
故答案为:(1﹣
)π.
分析: 先分别求出图②、图③、图④中阴影部分的面积,再从中发现规律,然后根据规律即可得出第n(n>1)个图形阴影部分的面积.
17.答案:10
解析:解:连接OC,
∵CD=4,OD=3,
在Rt△ODC中,
∴OC= =5,
∴AB=2OC=10,
故答案为:10.
分析:先连接OC,在Rt△ODC中,根据勾股定理得出OC的长,即可求出AB的长.
18.答案:证明:∵OA=OB,
∴∠A=∠B,
∵在△OAC和△OBD中:
,
∴△OAC≌△OBD(SAS).
解析:
根据等边对等角可以证得∠A=∠B,然后根据SAS即可证得两个三角形全等.
19.答案:解:如图,连接OB,
由AB=OC,得AB=OC,∠AOB=∠A.
由三角的外角等于与它不相邻的两个内角的和,得
∠EBO=∠A+∠AOB=2∠A.
由OB=OE,得∠E=∠EBO=2∠A.
由∠A+∠E=∠EOD,即∠A+2∠A=48°.
解得∠A=16°.
解析: 如图,连接OB,
根据圆的半径相等,可得等腰△BAO,根据等腰三角形的性质,可得∠A与∠AOB,∠B与∠E的关系,根据三角形的外角的性质,可得关于∠A的方程,根据解方程,可得答案.
20.答案:解:找到BC的中点E,连接AE,交半圆于P2,在半圆上取P1,连接AP1,EP1,
可见,AP1+EP1>AE,
即AP2是AP的最小值,
∵AE= = ,P2E=1,
∴AP2= ﹣1.
解析:找到BC的中点E,连接AE,交半圆于P2,在半圆上取P1,连接AP1,EP1,可见,AP1+EP1>AE,即AP2是AP的最小值,再根据勾股定理求出AE的长,然后减掉半径即可.
21.答案:解:∵AB、CD为⊙O中两条直径,∴OA=OB,OC=OD,∵CE=DF,∴OE=OF,在△AOF和△BOE中,,∴△AOF≌△BOE(SAS),∴AF=BE.分析:根据AB、CD为⊙O中两条直径,得出OA=OB,OC=OD,再根据CE=DF,得出OE=OF,从而证出△AOF和△BOE全等,即可得出答案.
解析:根据对圆的认识及全等三角形知识即可得出答案。
22.答案:解:①根据题意,画出图(1),
在△QOC中,OC=OQ,
∴∠OQC=∠OCP,
在△OPQ中,QP=QO,
∴∠QOP=∠QPO,
又∵∠AOC=30°,
∴∠QPO=∠OCP+∠AOC=∠OCP+30°,
在△OPQ中,∠QOP+∠QPO+∠OQC=180°,
即(∠OCP+30°)+(∠OCP+30°)+∠OCP=180°,
整理得,3∠OCP=120°,
∴∠OCP=40°.
②当P在线段OA的延长线上(如图2)
∵OC=OQ,
∴∠OQP=(180°﹣∠QOC)×①,
∵OQ=PQ,
∴∠OPQ=(180°﹣∠OQP)×②,
在△OQP中,30°+∠QOC+∠OQP+∠OPQ=180°③,
把①②代入③得∠QOC=20°,则∠OQP=80°
∴∠OCP=100°;
③当P在线段OA的反向延长线上(如图3),
∵OC=OQ,
∴∠OCP=∠OQC=(180°﹣∠COQ)×①,
∵OQ=PQ,
∴∠P=(180°﹣∠OQP)×②,
∵∠AOC=30°,
∴∠COQ+∠POQ=150°③,
∵∠P=∠POQ,2∠P=∠OCP=∠OQC④,
①②③④联立得
∠P=10°,
∴∠OCP=180°﹣150°﹣10°=20°.
故答案为:40°、20°、100°.
解析:点P是直线l上的一个动点,因而点P与线段AO有三种位置关系,在线段AO上,点P在OB上,点P在OA的延长线上.分这三种情况进行讨论即可.
将来的某一天,你会感谢曾经努力的自己!
3.1圆 同步练习
班级: 姓名:
一、选择题
1.下列命题中,正确的是( )
A.圆只有一条对称轴
B.圆的对称轴不止一条,但只有有限条
C.圆有无数条对称轴,每条直径都是它的对称轴
D.圆有无数条对称轴,经过圆心的每条直线都是它的对称轴
2.车轮要做成圆形,实际上就是根据圆的特征( )
A.同弧所对的圆周角相等 B.直径是圆中最大的弦
C.圆上各点到圆心的距离相等 D.圆是中心对称图形
3.由所有到已知点O的距离大于或等于3,并且小于或等于5的点组成的图形的面积为( )
A.4π B.9π C.16π D.25π
4.如图,在⊙O中,点B,O,C和点A,O,D分别在同一条直线上,则图中有( )条弦
A.2 B.3 C.4 D. 5
5.下列说法,正确的是( )
A.半径相等的两个圆大小相等 B.长度相等的两条弧是等弧
C.直径不一定是圆中最长的弦 D.圆上两点之间的部分叫做弦
6.Rt△ABC中,∠C=90°,AC=2,BC=4,如果以点A为圆心,AC为半径作⊙A,那么斜边中点D与⊙A的位置关系是( )
A.点D在⊙A外 B.点D在⊙A上 C.点D在⊙A内 D.无法确定
7.如图,AB是⊙O的直径,点C,D在⊙O上,且点C、D在AB的异侧,连结AD,OD,OC.若∠AOC=70°,且AD∥OC,则∠AOD的度数为( )
A.70° B.60° C.50° D.40°
8.如图,以坐标原点O为圆心的圆与y轴交于点A、B,且OA=1,则点B的坐标是( )
A.(0,1) B.(0,﹣1) C.( 1,0) D.(﹣1,0)
9.在△ABC中,若O为BC边的中点,则必有:AB2+AC2=2AO2+2BO2成立.依据以上结论,解决如下问题:如图,在矩形DEFG中,已知DE=4,EF=3,点P在以DE为直径的半圆上运动,则PF2+PG2的最小值为( )
A. B. C.34 D.10
10.在数轴上,点A所表示的实数为3,点B所表示的实数为a,⊙A的半径为2.那么下列说法中不正确的是( )
A.当a<1时,点B在⊙A外 B.当1<a<5时,点B在⊙A内
C.当a<5时,点B在⊙A内 D.当a>5时,点B在⊙A外
11.(2022九上·沭阳月考)一个点到圆的最大距离为11cm,最小距离为5cm,则圆的半径为( )
A.16cm或6cm, B.3cm或8cm C.3cm D.8cm
12.如图点A,D,G,B在半圆上,四边形ABOC,DEOF,HMNO均为矩形,设BC=a, EF=b, NH=c,则下列说法正确的是( )
A.a>b>c B.a=b=c C.c>a>b D.b>c>a
二、填空题
13.圆是轴对称图形,它的对称轴是 .
14.如图,MN为⊙O的弦,∠M=50°,则∠MON等于 .
15.如图,正方形ABCD的边长为2,E、F、G、H分别为各边中点,EG、FH相交于点O,以O为圆心,OE为半径画圆,则图中阴影部分的面积为 .
16.如图①是半径为1的圆,在其中挖去2个半径为 的圆得到图②,挖去22个半径为( )2的圆得到图③…,则第n(n>1)个图形阴影部分的面积是 .
17.如图,AB是⊙O的直径,点C在⊙O上,CD⊥AB,垂足为D,已知CD=4,OD=3,求AB的长是 .
三、解答题
18.已知:如图,在⊙O中,AB为弦,C、D两点在AB上,且AC=BD.
求证:△OAC≌△OBD.
19.如图,CD是⊙O的直径,E是⊙O上一点,∠EOD=48°,A为DC延长线上一点,且AB=OC,求∠A的度数.
20.如图,在Rt△ABC中,∠ACB=90°,AC=BC=2,以BC为直径的半圆交AB于D,P是 上的一个动点,连接AP,求AP的最小值.
21.如图,AB、CD为⊙O中两条直径,点E、F在直径CD上,且CE=DF.
求证:AF=BE.
22.如图,直线l经过⊙O的圆心O,且与⊙O交于A、B两点,点C在⊙O上,且∠AOC=30°,点P是直线l上的一个动点(与圆心O不重合),直线CP与⊙O相交于点Q.是否存在点P,使得QP=QO;若存在,求出相应的∠OCP的大小;若不存在,请简要说明理由.
答案解析部分
1.答案:D
解析:解:根据圆的性质和轴对称图形的定义可知:圆有无数条对称轴,每条直径所在的直线都是它的对称轴,由此可知D正确.
故答案为:D.
分析:轴对称图形:如果一个平面图形沿着一条直线折叠后,直线两旁的部分能够互相重合,这条直线叫做对称轴;根据圆的性质可知圆的对称轴是直径所在的直线.
2.答案:C
解析:根据圆的基本性质即可判断。
车轮要做成圆形,实际上就是根据圆上各点到圆心的距离相等,故选C.
【点评】本题属于基础应用题,只需学生熟练掌握圆的基本性质,即可完成。
3.答案:C
解析:解:由所有到已知点O的距离大于或等于3,并且小于或等于5的点组成的图形的面积是以5为半径的圆与以3为半径的圆组成的圆环的面积,
即π×52﹣π×32=16π,
故答案为:C.
分析:由所有到已知点O的距离大于或等于3,并且小于或等于5的点组成的图形的面积是以5为半径的圆与以3为半径的圆组成的圆环的面积,可得答案
4.答案:B
解析:圆中弦的定义:连接圆上任意两点的线段叫做弦。根据弦的定义可知,图中是弦的有:AB、BC、CE三条,则选项B符合题意。
故答案为:B
分析:首先要知道圆内弦的定义,其次利用弦定义解决问题。
5.答案:A
解析:A.根据半径确定圆的大小,故正确;
B.根据等弧的概念,长度相等的两条弧不一定能够重合,故错误;
C.根据三角形的两边之和大于第三边,可以证明直径是圆中最长的弦,故错误;
D.圆上任意两点间的部分叫弧,故错误.
故选A.
分析:理解等弧.直径.弦.弧的概念.
6.答案:A
【解析】解答:根据勾股定理求得斜边AB= =2 ,则AD= ,∵ >2,∴点在圆外.
故选A.
分析:本题根据点到圆心的距离和圆的半径之间的数量关系,来判断点和圆的位置关系.
7.答案:D
解析:解: ∵AD∥OC,
∴∠AOC=∠DAO=70°,
又∵OD=OA,
∴∠ADO=∠DAO=70°,
∴∠AOD=180﹣70°﹣70°=40°.
故答案为:D.
分析:根据平行线的性质,可求出∠DAO的度数,再根据等腰三角形的性质,可求得∠ODA的度数,然后利用三角形内角和定理求出∠AOD的度数。
8.答案:B
解析:解:∵以坐标原点O为圆心的圆与y轴交于点A、B,且OA=1,
∴点B的坐标是(0,﹣1).
故答案为:B
分析: 先根据同圆的半径相等得出OB=OA=1,再由点B在y轴的负半轴上即可求出点B的坐标.
9.答案:D
解析:解:设点M为DE的中点,点N为FG的中点,连接MN交半圆于点P,此时PN取最小值.
∵DE=4,四边形DEFG为矩形,
∴GF=DE,MN=EF,
∴MP=FN= DE=2,
∴NP=MN﹣MP=EF﹣MP=1,
∴PF2+PG2=2PN2+2FN2=2×12+2×22=10.
故答案为:D.
分析:设点M为DE的中点,点N为FG的中点,连接MN交半圆于点P,此时PN取最小值.根据矩形的性质得出GF=DE,MN=EF,根据同圆的半径相等得出MP=FN= DE=2,根据线段的和差,由NP=MN﹣MP=EF﹣MP得出NP的长,根据勾股定理及等式的性质即可由PF2+PG2=2PN2+2FN2算出答案。
10.答案:C
解析:解:A、a<1时,d>2,点B在⊙A外,故A正确;
B、当1<a<5时,点B在⊙A内,故B正确;
C、当1<a<5时,点B在⊙A内,故C错误;
D、当a>5时,点B在⊙A外,故D正确;
故选:C.
分析:根据当d>r时,点在圆外;当d=r时,点在圆上,当d<r时,点在圆内,可得答案.
11.答案:B
解析:若该点在圆外,则最大距离应该是过直径的线段,则直径=11-5=6cm,半径=cm,如图所示,
若该点在圆内,则最大距离应该是直径所包含的线段,则直径=11+5=16cm,半径=cm,如图所示,
分析:应该先分析出有几种情况,再利用点与圆的位置关系进行半径的计算。
12.答案:B
解析:由于四边形ABOC,DEOF,HMNO均为矩形,因此具有对角线相等的性质。连接OA、OD和OM,则OA=BC=a,OD=BF=b,OM=NH=c,又因为OA、OD和OM均为半径且相等,则a=b=c,B选项符合题意,故答案为:B。
分析:首先要将a、b、c转换为已知可求解的线段(本题为半径),最后利用圆的半径相等性质进行大小关系的比较。
13.答案:直径所在的直线
解析:解:依题可得:圆的对称轴是直径所在的直线.
故答案为:直径所在的直线.
分析:轴对称图形:一个图形沿一条直线折叠,直线两旁的部分能够完全重合的图形;这条直线叫做对称轴;结合圆的性质即可得出答案.
14.答案:80°
解析:解:∵OM=ON,
∴∠N=∠M=50°,
∴∠MON=180°﹣∠M﹣∠N=80°,
故答案为80°.
分析:利用等腰三角形的性质可得∠N的度数,根据三角形的内角和定理可得所求角的度数.
15.答案:
解析:解:由题意可得:OE=1,
阴影面积= = .
分析: 根据圆及正方形的对称性可知:图中阴影部分的半径其实质就是一个半圆的面积,根据半圆面积计算方法即可算出答案。
16.答案:(1﹣ )π
解析:解:图②中阴影部分的面积为:π×1
2﹣π×(
)
2×2=π﹣
π=(1﹣
)π=
π;
图③中阴影部分的面积为:π×12﹣π×[(
)2]2×22=π﹣
π=(1﹣
)π=
π;
图④是半径为1的圆,在其中挖去23个半径为(
)3的圆得到的,则图④中阴影部分的面积为:π×12﹣π×[(
)3]2×23=π﹣
π=(1﹣
)π=
π;
…,
则第n(n>1)个图形阴影部分的面积为:π×12﹣π×[(
)n﹣1]2×2n﹣1=π﹣
π=(1﹣
)π.
故答案为:(1﹣
)π.
分析: 先分别求出图②、图③、图④中阴影部分的面积,再从中发现规律,然后根据规律即可得出第n(n>1)个图形阴影部分的面积.
17.答案:10
解析:解:连接OC,
∵CD=4,OD=3,
在Rt△ODC中,
∴OC= =5,
∴AB=2OC=10,
故答案为:10.
分析:先连接OC,在Rt△ODC中,根据勾股定理得出OC的长,即可求出AB的长.
18.答案:证明:∵OA=OB,
∴∠A=∠B,
∵在△OAC和△OBD中:
,
∴△OAC≌△OBD(SAS).
解析:
根据等边对等角可以证得∠A=∠B,然后根据SAS即可证得两个三角形全等.
19.答案:解:如图,连接OB,
由AB=OC,得AB=OC,∠AOB=∠A.
由三角的外角等于与它不相邻的两个内角的和,得
∠EBO=∠A+∠AOB=2∠A.
由OB=OE,得∠E=∠EBO=2∠A.
由∠A+∠E=∠EOD,即∠A+2∠A=48°.
解得∠A=16°.
解析: 如图,连接OB,
根据圆的半径相等,可得等腰△BAO,根据等腰三角形的性质,可得∠A与∠AOB,∠B与∠E的关系,根据三角形的外角的性质,可得关于∠A的方程,根据解方程,可得答案.
20.答案:解:找到BC的中点E,连接AE,交半圆于P2,在半圆上取P1,连接AP1,EP1,
可见,AP1+EP1>AE,
即AP2是AP的最小值,
∵AE= = ,P2E=1,
∴AP2= ﹣1.
解析:找到BC的中点E,连接AE,交半圆于P2,在半圆上取P1,连接AP1,EP1,可见,AP1+EP1>AE,即AP2是AP的最小值,再根据勾股定理求出AE的长,然后减掉半径即可.
21.答案:解:∵AB、CD为⊙O中两条直径,∴OA=OB,OC=OD,∵CE=DF,∴OE=OF,在△AOF和△BOE中,,∴△AOF≌△BOE(SAS),∴AF=BE.分析:根据AB、CD为⊙O中两条直径,得出OA=OB,OC=OD,再根据CE=DF,得出OE=OF,从而证出△AOF和△BOE全等,即可得出答案.
解析:根据对圆的认识及全等三角形知识即可得出答案。
22.答案:解:①根据题意,画出图(1),
在△QOC中,OC=OQ,
∴∠OQC=∠OCP,
在△OPQ中,QP=QO,
∴∠QOP=∠QPO,
又∵∠AOC=30°,
∴∠QPO=∠OCP+∠AOC=∠OCP+30°,
在△OPQ中,∠QOP+∠QPO+∠OQC=180°,
即(∠OCP+30°)+(∠OCP+30°)+∠OCP=180°,
整理得,3∠OCP=120°,
∴∠OCP=40°.
②当P在线段OA的延长线上(如图2)
∵OC=OQ,
∴∠OQP=(180°﹣∠QOC)×①,
∵OQ=PQ,
∴∠OPQ=(180°﹣∠OQP)×②,
在△OQP中,30°+∠QOC+∠OQP+∠OPQ=180°③,
把①②代入③得∠QOC=20°,则∠OQP=80°
∴∠OCP=100°;
③当P在线段OA的反向延长线上(如图3),
∵OC=OQ,
∴∠OCP=∠OQC=(180°﹣∠COQ)×①,
∵OQ=PQ,
∴∠P=(180°﹣∠OQP)×②,
∵∠AOC=30°,
∴∠COQ+∠POQ=150°③,
∵∠P=∠POQ,2∠P=∠OCP=∠OQC④,
①②③④联立得
∠P=10°,
∴∠OCP=180°﹣150°﹣10°=20°.
故答案为:40°、20°、100°.
解析:点P是直线l上的一个动点,因而点P与线段AO有三种位置关系,在线段AO上,点P在OB上,点P在OA的延长线上.分这三种情况进行讨论即可.
将来的某一天,你会感谢曾经努力的自己!
