2023-2024学年北师大版九年级下册3.3垂径定理 同步练习(含解析)
文档属性
| 名称 | 2023-2024学年北师大版九年级下册3.3垂径定理 同步练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1011.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-19 16:55:36 | ||
图片预览


文档简介
2023-2024学年北师大版九年级下册同步练习【提升卷】
3.3垂径定理 同步练习
姓名: 班级:
一、选择题
1.下列说法中,正确的是( ).
A.在同圆或等圆中,相等的圆心角所对的弧相等
B.平分弦的直径垂直于弦
C.长度相等的两条弧相等
D.圆是轴对称图形,任何一条直径都是它的对称轴
2.(2023九下·宿迁开学考)如图,在半径为5的⊙O中,弦AB=6,OP⊥AB,垂足为点P,则OP的长为( )
A.2.5 B.3 C.3.5 D.4
3.如图所示,的半径为13,弦AB的长为24,M是弦AB上的动点,则线段OM长的最小值为( ).
A.8 B.7 C.6 D.5
4.如图所示,已知的直径于点,则下列结论中,不一定正确的是( ).
A. B.
C. D.
5.下列命题:(1)垂直于弦的直线平分弦;(2)平分弦的直径必垂直于弦,并且平分弦所对的两条弧;(3)平分弦的直线必过圆心;(4)弦所对的两条弧的中点连线垂直平分弦。其中正确的命题有( )
A.1个 B.2个 C.3个 D.4个
6.⊙O的半径为5cm,弦AB//CD,且AB=8cm,CD=6cm,则AB与CD之间的距离为( )
A.1 cm B.7cm C.3 cm或4 cm D.1cm 或7cm
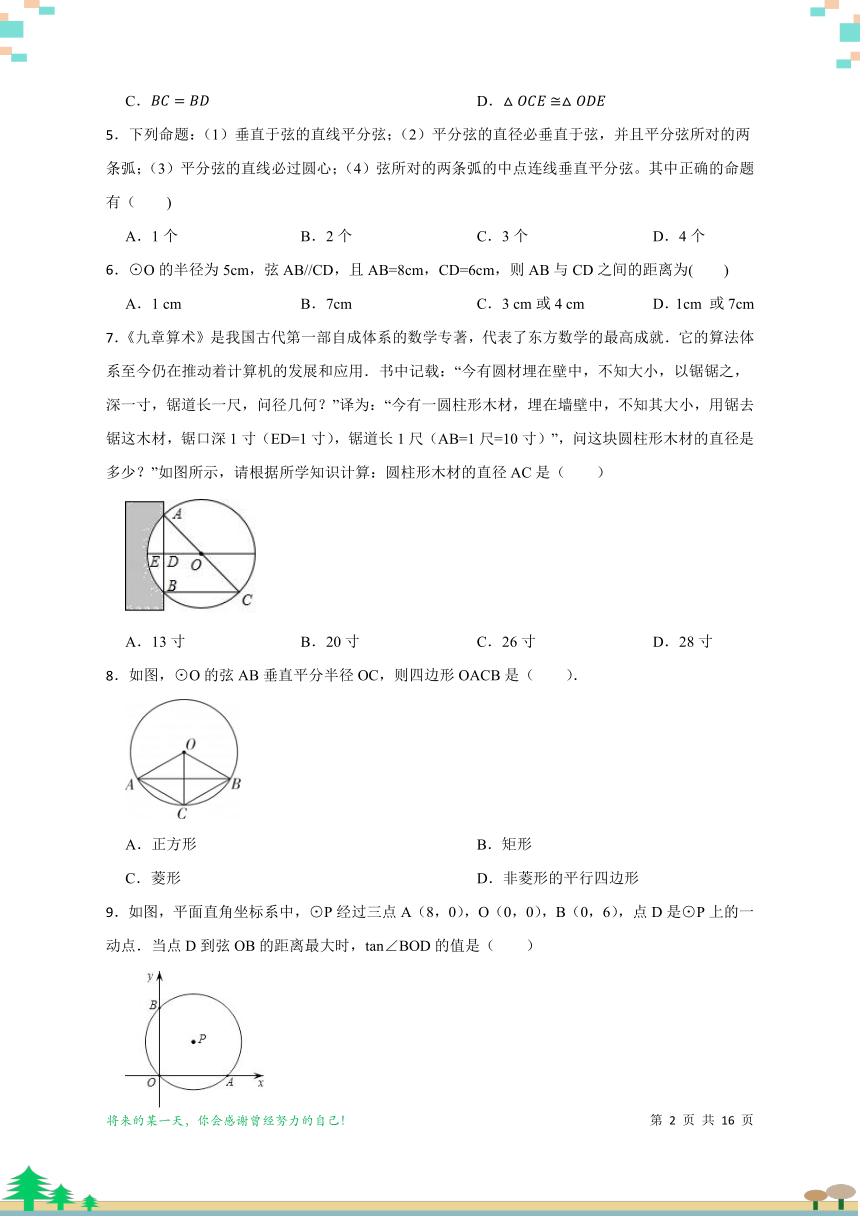
7.《九章算术》是我国古代第一部自成体系的数学专著,代表了东方数学的最高成就.它的算法体系至今仍在推动着计算机的发展和应用.书中记载:“今有圆材埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”译为:“今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯这木材,锯口深1寸(ED=1寸),锯道长1尺(AB=1尺=10寸)”,问这块圆柱形木材的直径是多少?”如图所示,请根据所学知识计算:圆柱形木材的直径AC是( )
A.13寸 B.20寸 C.26寸 D.28寸
8.如图,⊙O的弦AB垂直平分半径OC,则四边形OACB是( ).
A.正方形 B.矩形
C.菱形 D.非菱形的平行四边形
9.如图,平面直角坐标系中,⊙P经过三点A(8,0),O(0,0),B(0,6),点D是⊙P上的一动点.当点D到弦OB的距离最大时,tan∠BOD的值是( )
A.2 B.3 C.4 D.5
10.在圆柱形油槽内装有一些油.截面如图,油面宽AB为6分米,如果再注入一些油后,油面AB上升1分米,油面宽变为8分米,圆柱形油槽直径MN为( )
A.6分米 B.8分米 C.10分米 D.12分米
11.已知⊙O的半径为2,点P是⊙O内一点,且OP= ,过P作互相垂直的两条弦AC、BD,则四边形ABCD面积的最大值为( )
A.4 B.5 C.6 D.7
12.如图,⊙O的直径AB=10,E在⊙O内,且OE=4,则过E点所有弦中,长度为整数的条数为( )
A.4 B.6 C.8 D.10
二、填空题
13.垂径定理:垂直于弦的直径平分 ,并且平分 ,这里的“弧"包括弦所对的两条弧.
14.半径为6cm的圆中,垂直平分半径OA的弦长为 cm.
15.垂径定理的应用:如图所示,已知AB为的直径,并且,根据垂径定理可得: , , .
16.下列说法不正确的是 (只需填写序号).
①平分弧的直径垂直平分弧所对的弦;
②平分弦的直径平分弦所对的弧;
③垂直平分弦的直线必定经过圆心;
④平分弦的直径垂直于弦.
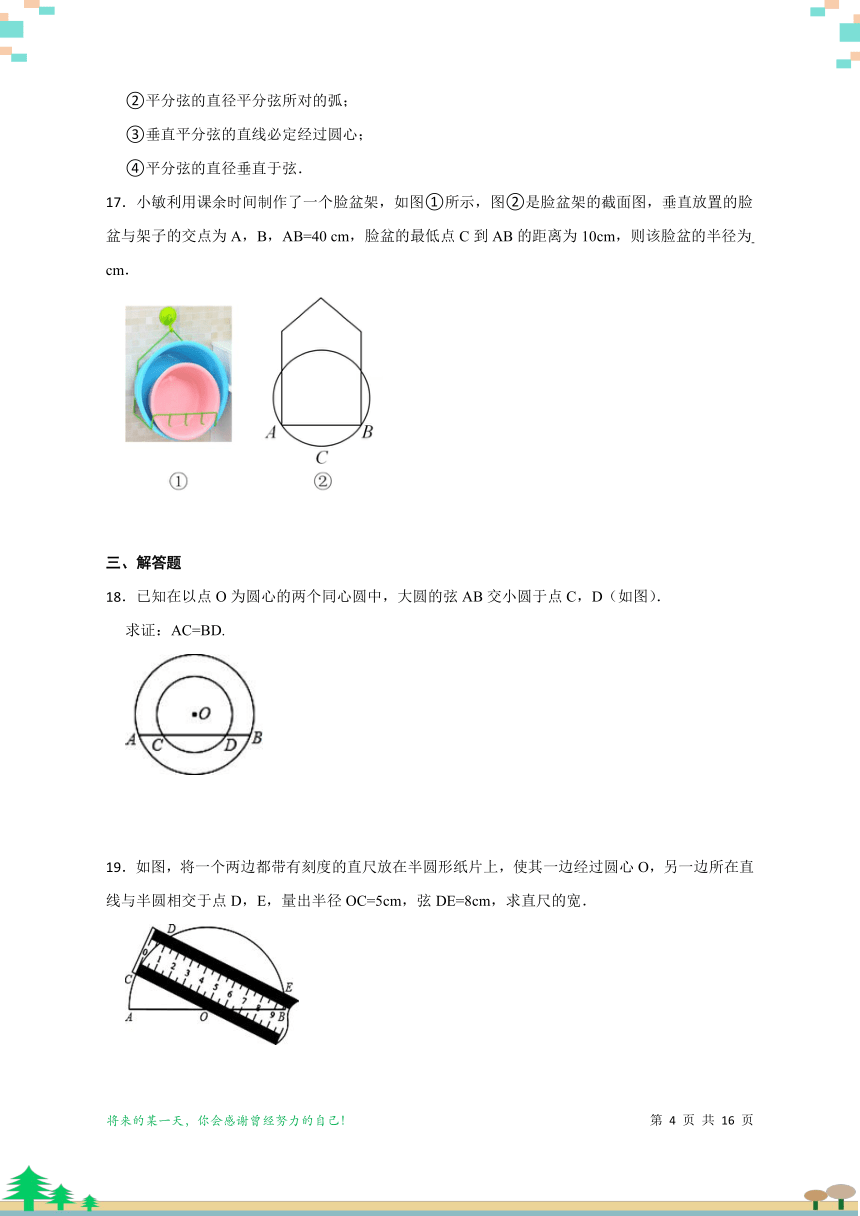
17.小敏利用课余时间制作了一个脸盆架,如图①所示,图②是脸盆架的截面图,垂直放置的脸盆与架子的交点为A,B,AB=40 cm,脸盆的最低点C到AB的距离为10cm,则该脸盆的半径为 cm.
三、解答题
18.已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D(如图).
求证:AC=BD.
19.如图,将一个两边都带有刻度的直尺放在半圆形纸片上,使其一边经过圆心O,另一边所在直线与半圆相交于点D,E,量出半径OC=5cm,弦DE=8cm,求直尺的宽.
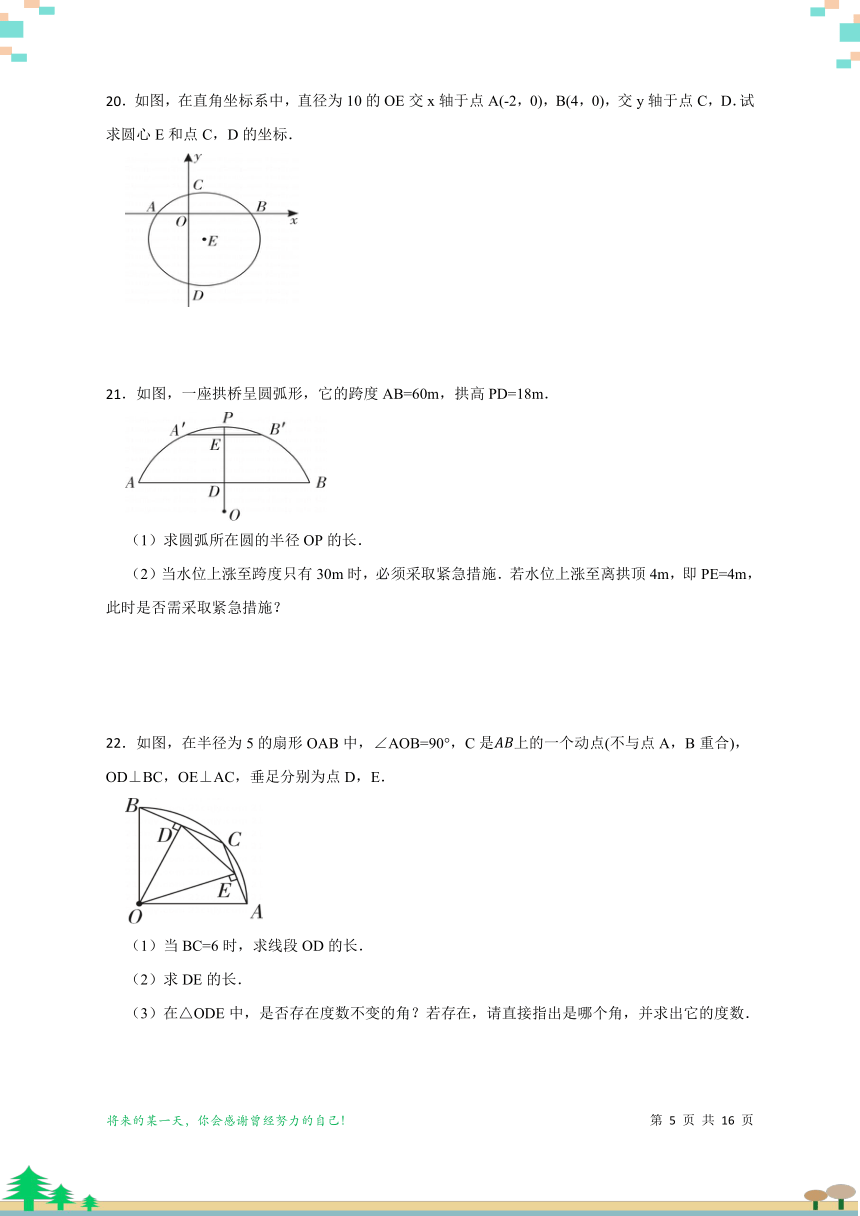
20.如图,在直角坐标系中,直径为10的OE交x轴于点A(-2,0),B(4,0),交y轴于点C,D.试求圆心E和点C,D的坐标.
21.如图,一座拱桥呈圆弧形,它的跨度AB=60m,拱高PD=18m.
(1)求圆弧所在圆的半径OP的长.
(2)当水位上涨至跨度只有30m时,必须采取紧急措施.若水位上涨至离拱顶4m,即PE=4m,此时是否需采取紧急措施?
22.如图,在半径为5的扇形OAB中,∠AOB=90°,C是上的一个动点(不与点A,B重合),OD⊥BC,OE⊥AC,垂足分别为点D,E.
(1)当BC=6时,求线段OD的长.
(2)求DE的长.
(3)在△ODE中,是否存在度数不变的角?若存在,请直接指出是哪个角,并求出它的度数.
答案解析部分
1.答案:A
解析:A、 在同圆或等圆中,相等的圆心角所对的弧相等 ,故原命题正确,不符合题意;
B、 由平分弦(不是直径)的直径垂直于弦 ,可知原命题错误,不符合题意;
C、由能完全重合的两条弧是等弧,可知原命题错误,不符合题意;
D、由圆是轴对称图形,任何一条直径所在的直线都是它的对称轴,可知原命题错误,不符合题意.
故答案为:A.
分析:由在同圆或等圆中,相等的圆心角所对的弧相等 ,可判断A选项; 由平分弦(不是直径)的直径垂直于弦 ,可判断B选项;由能完全重合的两条弧是等弧,可判断C选项;由圆是轴对称图形,任何一条直径所在的直线都是它的对称轴,可判断D选项.
2.答案:D
解析:解:连接OA,
∵OP⊥AB,
∴AP=BP=3 ,
在直角三角形AOP中,
故答案为:D.
分析:连接OA,根据垂径定理得AP=3,在Rt△AOP中,利用勾股定理计算可得OP.
3.答案:D
解析:解:如图,过点O作OC⊥AB于点C,连接OB,
∵OC⊥AB,
∴∠OCB=90°,BC=AB=12,
在Rt△BCO中,由勾股定理得OC=,
∴OM≥OC,
∴OM的最小值为5.
故答案为:D.
分析:过点O作OC⊥AB于点C,连接OB,由垂径定理得∠OCB=90°,BC=AB=12,在Rt△BCO中,由勾股定理算出OC,进而根据垂线段最短可得OM≥OC,从而即可得出答案.
4.答案:B
解析:解:∵圆O的直径AB⊥CD,∴CE=DE,弧BC=弧BD,故A、C选项都正确;
∵OC=OD,OE=OE,CE=DE,∴△COE≌△DOE(SSS),故D选项正确;
不能证出AE=OE,故B选项不一定正确.
故答案为:B.
分析:由垂直弦的直径平分弦,并且平分弦所对的两条弧,可直接判断A、C选项,由SSS可判断出△COE≌△DOE,从而可判断D选项;不能证出AE=OE,据此可判断B选项.
5.答案:A
解析:解:(1)垂直于弦的直径平分弦,错误;(2)平分弦(不是直径)的直径必垂直于弦,并且平分弦所对的两条弧,错误;(3)垂直于弦且平分弦的直线必过圆心,错误;(4)弦所对的两条弧的中点连线垂直平分弦.正确;
其中正确的命题有1个.
故答案为:A.
分析:垂径定理及其推论有:垂直与弦的直径平分弦,并且平分弦所对的弧;连接弦所对的两条弧的中点的直线垂直与弦,且经过圆心;垂直平分弦的直线必过圆心,且平分弦所对的弧.根据这些定理即可判断。
6.答案:B
解析:设与这两条平行的弦有一条直径,当这两条线位于直径的同侧时候根据垂径定理和勾股定理可以得出两条平行弦之间的距离为1.当位居直径的两侧时候,那么答案为7.
分析:此题考查了垂径定理和勾股定理知识点,注意相应的问题要具体分析.
7.答案:C
解析:解: 设⊙O的半径为r.
在Rt△ADO中,AD=5,OD=r﹣1,OA=r,
则有r2=52+(r﹣1)2,
解得r=13,
∴⊙O的直径为26寸,
故答案为:C.
分析:在Rt△ADO中,用勾股定理可得关于半径的方程,解方程即可求得半径的值,则 直径AC等于半径的两倍。
8.答案:C
解析:解:记AB与OC的交点为D,如图,
∵弦AB垂直平分半径OC,
∴OD=CD,AD=BD,OC⊥AB,
∴四边形OACB是平行四边形,
又OC⊥AB,
∴四边形OACB是菱形.
故答案为:C.
分析:记AB与OC的交点为D,根据垂径定理得AD=BD,OC⊥AB,由题意易得OD=CD,从而利用对角线互相平分的四边形是平行四边形得四边形OACB是平行四边形,最后根据对角线互相垂直的平行四边形是菱形得出结论.
9.答案:B
解析:如图,连接AB,过点P作PE⊥BO,并延长EP交⊙P于点D,此时点D到弦OB的距离最大,
∵A(8,0),B(0,6),
∴AO=8,BO=6,
∵∠BOA=90°,
∴AB= =10,则⊙P的半径为5,
∵PE⊥BO,
∴BE=EO=3,
∴PE= =4,
∴ED=9,
∴tan∠BOD= =3,
故答案为:B.
分析:如图,连接AB,过点P作PE⊥BO,并延长EP交⊙P于点D,此时点D到弦OB的距离最大,在Rt△AOB中,利用勾股定理算出AB的长,即可得出该圆的半径,根据垂径定理得BE=EO=3,再根据勾股定理算出PE的长,从而得出ED的长,最后根据正切函数的定义即可算出答案。
10.答案:C
解析:解:如图,
依题意得AB=6,CD=8,过O点作AB的垂线,垂足为E,交CD于F点,连接OA,OC,由垂径定理,得AE= AB=3,CF= CD=4,
设OE=x,则OF=x﹣1,
在Rt△OAE中,OA2=AE2+OE2,
在Rt△OCF中,OC2=CF2+OF2,
∵OA=OC,
∴32+x2=42+(x﹣1)2,
解得x=4,
∴半径OA= =5,
∴直径MN=2OA=10分米.
故答案为:C.
分析:过O点作AB的垂线,垂足为E,交CD于F点,连接OA、OC,由垂径定理可知AE= AB=3、CF=CD=4,设OE=x,在Rt△OAE和Rt△OCF中,利用斜边相等借助勾股定理列出x的方程,据此即可解答。
11.答案:B
解析:解:如图:连接OA、OD,作OE⊥AC于E,OF⊥BD于F,
∵AC⊥BD,
∴四边形OEPF为矩形,
∵OA=OD=2,OP= ,
设OE为x(x>0),
根据勾股定理得,OF=EP= = ,
在Rt△AOE中,AE= =
∴AC=2AE=2 ,
同理得,BD=2DF=2 =2 ,
又∵任意对角线互相垂直的四边形的面积等于对角线乘积的 ,
∴S四边形ABCD= AC×BD= ×2 ×2 =2 =2
当x2= 即:x= 时,四边形ABCD的面积最大,等于2 =5.
答案为:B.
分析:作出弦心距,根据S四边形ABCD=对角线乘积的一半,列出函数关系式,配成顶点式,求出最值.
12.答案:C
解析:解:∵AB=10,
∵OB=OA=OC=5,
过E作CD⊥AB于E,连接OC,则CD是过E的⊙O的最短的弦,
∵OB⊥CD,
∴∠CEO=90°,
由勾股定理得:CE= = =3,
∵OE⊥CD,OE过O,
∴CD=2CE=6,
∵AB是过E的⊙O的最长弦,AB=10,
∴过E点所有弦中,长度为整数的条数为1+2+2+2+1=8,
答案为:C.
分析:求出过E的最短的弦,就是以OE为弦心距的弦,最长的弦就是直径,在这个范围内取整数,注意对称性.
13.答案:这条弦;弦所对的弧
解析: 垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的弧,这里的“弧"包括弦所对的两条弧.
故答案为:这条弦 , 弦所对的弧.
分析:根据垂径定理填空即可.
14.答案:
解析:据垂径定理和股定理可以求的弦长为6 .
分析:此题考查了垂径定理和勾股定理知识点.
15.答案:;;
解析:解:∵AB是圆O的直径,且AB⊥CD,
∴CE=DE,,.
故答案为:CE=DE,,.
分析:由垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的弧可直接得出答案.
16.答案:②④
解析:解:①因为平分弧的直径一定垂直于弦,所以一定平分弧所对的弦;故①正确;
②因为平分弦(不是直径)的直径平分弦所对的弧;故②错误;
③因为平分弦的直径垂直于弦,所以垂直平分弦的直线必经过圆心,故③正确;
④因为平分弦(非直径)的直径一定垂直于弦,故④错误;
故答案为:②④.
分析:根据垂直于弦的直径平分这条弦,并且平分弦所对的两条弧;平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;弦的垂直平分线经过圆心,并且平分弦所对的两条弧;平分弦所对一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧进行分析即可得出答案.
17.答案:25
解析:解:设脸盆所在圆的圆心为O,连接OC交AB于点D,连接OA,如图:
∴
设脸盆的半径为xcm,则
在中,
即
解得:
则该脸盆的半径为25cm.
故答案为:25.
分析:设圆心为O,连接OC交AB于点D,连接OA,根据垂径定理得AD=BD=AB=20cm,设脸盆的半径为xcm,则OD=(x-10)cm,在Rt△AOD中,根据勾股定理列方程,解方程即可求解.
18.答案:解:过O作OE⊥AB于点E,
则CE=DE,AE=BE,
∴BE-DE=AE-CE.
即AC=BD.
解析:过O作OE⊥AB于点E,根据垂径定理可知CE=DE、AE=BE,利用等式性质即可证明。
19.答案:解:过点O作OM⊥DE于点M,连接OD.
∴DM= .
∵DE=8(cm)
∴DM=4(cm)
在Rt△ODM中,∵OD=OC=5(cm),
∴OM= = =3(cm)
∴直尺的宽度为3cm.
解析:过点O作OM⊥DE于点M,连接OD,由垂径定理可知DM= DE=4,在Rt△ODM中借助勾股定理即可解答。
20.答案:解:过E作EF⊥AB于F,EG⊥CD于G,连接EB,CE,DE,如图:
∵A、B的坐标分别为(-2,0)、(4,0),
∴AB=6,OB=4,
∵EF⊥AB,
∴,
∴OF=1,
∵⊙E的直径为10,
∴半径EB=5,
∴,
∴E的坐标是(1,-4).
则EG=1,
∴,
则
∴点C的坐标是,
则
点D的坐标是.
解析:过E作EF⊥AB于F,EG⊥CD于G,连接EB,CE,DE,先根据A、B点的坐标求出AB的长,再根据垂径定理求出BF的长,即可求出OF的长,再利用直角三角形中两直角边的平方和等于斜边的平方求出EF的值,得出E点坐标,再利用直角三角形中两直角边的平方和等于斜边的平方求出CG的值,即可求出点C和点D的坐标.
21.答案:(1)解: 连接OA,如图:
由题意得:(米),OD=(r-18)米,
在Rt△ADO中,由勾股定理得:r2=302+(r-18)2,
解得:r=34(米);
即OP=34m.
(2)解: 连接OA′,
∵OE=OP-PE=30米,
∴在Rt△A′EO中,由勾股定理得:A′E2=A′O2-OE2,即:A′E2=342-302,
解得:A′E=16(米).
∴A′B′=32(米).
∵A′B′=32>30,
∴不需要采取紧急措施.
解析:(1)连接OA,利用r表示出OP的长,在Rt△AOD中,根据直角三角形中两直角边的平方和等于斜边的平方求出r的值即可;
(2)连接OA′,在Rt△A′EO中,由直角三角形中两直角边的平方和等于斜边的平方得出A′E的长,进而可得出A′B′的长,据此可得出结论.
22.答案:(1)解:∵OD⊥BC,
∴BD=BC= ×6=3,
∵∠BDO= 90°,OB=5,BD=3,
OD= =4,
即线段OD的长为4;
(2)解:如图,连结AB,DE,
∵∠AOB=90° ,OA=OB=5,
∴AB= .
∵OD⊥BC,OE⊥AC,
∴D,E分别是线段BC,AC的中点,
∴DE是△ABC的中位线,
∴DE=AB= ;
(3)解:∠DOE的度数不变,为45°,理由如下:
设OD交弧BC于点M,OE交弧AC于点N,
∵
∴
∴
∵
∴
即
解析:(1)根据垂径定理得到BD=BC,在Rt△BDO中利用勾股定理即可求出OD的长;
(2)连结AB,在Rt△AOB中,利用勾股定理求出AB的长,由垂径定理得D,E分别是线段BC,AC的中点,最后根据三角形中位线定理即可求出DE的长;
(3)∠DOE的度数不变,为45°,理由如下:根据垂径定理即可求得,进而根据圆心角、弧、弦的关系可求出∠DOE的度数.
将来的某一天,你会感谢曾经努力的自己!
3.3垂径定理 同步练习
姓名: 班级:
一、选择题
1.下列说法中,正确的是( ).
A.在同圆或等圆中,相等的圆心角所对的弧相等
B.平分弦的直径垂直于弦
C.长度相等的两条弧相等
D.圆是轴对称图形,任何一条直径都是它的对称轴
2.(2023九下·宿迁开学考)如图,在半径为5的⊙O中,弦AB=6,OP⊥AB,垂足为点P,则OP的长为( )
A.2.5 B.3 C.3.5 D.4
3.如图所示,的半径为13,弦AB的长为24,M是弦AB上的动点,则线段OM长的最小值为( ).
A.8 B.7 C.6 D.5
4.如图所示,已知的直径于点,则下列结论中,不一定正确的是( ).
A. B.
C. D.
5.下列命题:(1)垂直于弦的直线平分弦;(2)平分弦的直径必垂直于弦,并且平分弦所对的两条弧;(3)平分弦的直线必过圆心;(4)弦所对的两条弧的中点连线垂直平分弦。其中正确的命题有( )
A.1个 B.2个 C.3个 D.4个
6.⊙O的半径为5cm,弦AB//CD,且AB=8cm,CD=6cm,则AB与CD之间的距离为( )
A.1 cm B.7cm C.3 cm或4 cm D.1cm 或7cm
7.《九章算术》是我国古代第一部自成体系的数学专著,代表了东方数学的最高成就.它的算法体系至今仍在推动着计算机的发展和应用.书中记载:“今有圆材埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”译为:“今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯这木材,锯口深1寸(ED=1寸),锯道长1尺(AB=1尺=10寸)”,问这块圆柱形木材的直径是多少?”如图所示,请根据所学知识计算:圆柱形木材的直径AC是( )
A.13寸 B.20寸 C.26寸 D.28寸
8.如图,⊙O的弦AB垂直平分半径OC,则四边形OACB是( ).
A.正方形 B.矩形
C.菱形 D.非菱形的平行四边形
9.如图,平面直角坐标系中,⊙P经过三点A(8,0),O(0,0),B(0,6),点D是⊙P上的一动点.当点D到弦OB的距离最大时,tan∠BOD的值是( )
A.2 B.3 C.4 D.5
10.在圆柱形油槽内装有一些油.截面如图,油面宽AB为6分米,如果再注入一些油后,油面AB上升1分米,油面宽变为8分米,圆柱形油槽直径MN为( )
A.6分米 B.8分米 C.10分米 D.12分米
11.已知⊙O的半径为2,点P是⊙O内一点,且OP= ,过P作互相垂直的两条弦AC、BD,则四边形ABCD面积的最大值为( )
A.4 B.5 C.6 D.7
12.如图,⊙O的直径AB=10,E在⊙O内,且OE=4,则过E点所有弦中,长度为整数的条数为( )
A.4 B.6 C.8 D.10
二、填空题
13.垂径定理:垂直于弦的直径平分 ,并且平分 ,这里的“弧"包括弦所对的两条弧.
14.半径为6cm的圆中,垂直平分半径OA的弦长为 cm.
15.垂径定理的应用:如图所示,已知AB为的直径,并且,根据垂径定理可得: , , .
16.下列说法不正确的是 (只需填写序号).
①平分弧的直径垂直平分弧所对的弦;
②平分弦的直径平分弦所对的弧;
③垂直平分弦的直线必定经过圆心;
④平分弦的直径垂直于弦.
17.小敏利用课余时间制作了一个脸盆架,如图①所示,图②是脸盆架的截面图,垂直放置的脸盆与架子的交点为A,B,AB=40 cm,脸盆的最低点C到AB的距离为10cm,则该脸盆的半径为 cm.
三、解答题
18.已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D(如图).
求证:AC=BD.
19.如图,将一个两边都带有刻度的直尺放在半圆形纸片上,使其一边经过圆心O,另一边所在直线与半圆相交于点D,E,量出半径OC=5cm,弦DE=8cm,求直尺的宽.
20.如图,在直角坐标系中,直径为10的OE交x轴于点A(-2,0),B(4,0),交y轴于点C,D.试求圆心E和点C,D的坐标.
21.如图,一座拱桥呈圆弧形,它的跨度AB=60m,拱高PD=18m.
(1)求圆弧所在圆的半径OP的长.
(2)当水位上涨至跨度只有30m时,必须采取紧急措施.若水位上涨至离拱顶4m,即PE=4m,此时是否需采取紧急措施?
22.如图,在半径为5的扇形OAB中,∠AOB=90°,C是上的一个动点(不与点A,B重合),OD⊥BC,OE⊥AC,垂足分别为点D,E.
(1)当BC=6时,求线段OD的长.
(2)求DE的长.
(3)在△ODE中,是否存在度数不变的角?若存在,请直接指出是哪个角,并求出它的度数.
答案解析部分
1.答案:A
解析:A、 在同圆或等圆中,相等的圆心角所对的弧相等 ,故原命题正确,不符合题意;
B、 由平分弦(不是直径)的直径垂直于弦 ,可知原命题错误,不符合题意;
C、由能完全重合的两条弧是等弧,可知原命题错误,不符合题意;
D、由圆是轴对称图形,任何一条直径所在的直线都是它的对称轴,可知原命题错误,不符合题意.
故答案为:A.
分析:由在同圆或等圆中,相等的圆心角所对的弧相等 ,可判断A选项; 由平分弦(不是直径)的直径垂直于弦 ,可判断B选项;由能完全重合的两条弧是等弧,可判断C选项;由圆是轴对称图形,任何一条直径所在的直线都是它的对称轴,可判断D选项.
2.答案:D
解析:解:连接OA,
∵OP⊥AB,
∴AP=BP=3 ,
在直角三角形AOP中,
故答案为:D.
分析:连接OA,根据垂径定理得AP=3,在Rt△AOP中,利用勾股定理计算可得OP.
3.答案:D
解析:解:如图,过点O作OC⊥AB于点C,连接OB,
∵OC⊥AB,
∴∠OCB=90°,BC=AB=12,
在Rt△BCO中,由勾股定理得OC=,
∴OM≥OC,
∴OM的最小值为5.
故答案为:D.
分析:过点O作OC⊥AB于点C,连接OB,由垂径定理得∠OCB=90°,BC=AB=12,在Rt△BCO中,由勾股定理算出OC,进而根据垂线段最短可得OM≥OC,从而即可得出答案.
4.答案:B
解析:解:∵圆O的直径AB⊥CD,∴CE=DE,弧BC=弧BD,故A、C选项都正确;
∵OC=OD,OE=OE,CE=DE,∴△COE≌△DOE(SSS),故D选项正确;
不能证出AE=OE,故B选项不一定正确.
故答案为:B.
分析:由垂直弦的直径平分弦,并且平分弦所对的两条弧,可直接判断A、C选项,由SSS可判断出△COE≌△DOE,从而可判断D选项;不能证出AE=OE,据此可判断B选项.
5.答案:A
解析:解:(1)垂直于弦的直径平分弦,错误;(2)平分弦(不是直径)的直径必垂直于弦,并且平分弦所对的两条弧,错误;(3)垂直于弦且平分弦的直线必过圆心,错误;(4)弦所对的两条弧的中点连线垂直平分弦.正确;
其中正确的命题有1个.
故答案为:A.
分析:垂径定理及其推论有:垂直与弦的直径平分弦,并且平分弦所对的弧;连接弦所对的两条弧的中点的直线垂直与弦,且经过圆心;垂直平分弦的直线必过圆心,且平分弦所对的弧.根据这些定理即可判断。
6.答案:B
解析:设与这两条平行的弦有一条直径,当这两条线位于直径的同侧时候根据垂径定理和勾股定理可以得出两条平行弦之间的距离为1.当位居直径的两侧时候,那么答案为7.
分析:此题考查了垂径定理和勾股定理知识点,注意相应的问题要具体分析.
7.答案:C
解析:解: 设⊙O的半径为r.
在Rt△ADO中,AD=5,OD=r﹣1,OA=r,
则有r2=52+(r﹣1)2,
解得r=13,
∴⊙O的直径为26寸,
故答案为:C.
分析:在Rt△ADO中,用勾股定理可得关于半径的方程,解方程即可求得半径的值,则 直径AC等于半径的两倍。
8.答案:C
解析:解:记AB与OC的交点为D,如图,
∵弦AB垂直平分半径OC,
∴OD=CD,AD=BD,OC⊥AB,
∴四边形OACB是平行四边形,
又OC⊥AB,
∴四边形OACB是菱形.
故答案为:C.
分析:记AB与OC的交点为D,根据垂径定理得AD=BD,OC⊥AB,由题意易得OD=CD,从而利用对角线互相平分的四边形是平行四边形得四边形OACB是平行四边形,最后根据对角线互相垂直的平行四边形是菱形得出结论.
9.答案:B
解析:如图,连接AB,过点P作PE⊥BO,并延长EP交⊙P于点D,此时点D到弦OB的距离最大,
∵A(8,0),B(0,6),
∴AO=8,BO=6,
∵∠BOA=90°,
∴AB= =10,则⊙P的半径为5,
∵PE⊥BO,
∴BE=EO=3,
∴PE= =4,
∴ED=9,
∴tan∠BOD= =3,
故答案为:B.
分析:如图,连接AB,过点P作PE⊥BO,并延长EP交⊙P于点D,此时点D到弦OB的距离最大,在Rt△AOB中,利用勾股定理算出AB的长,即可得出该圆的半径,根据垂径定理得BE=EO=3,再根据勾股定理算出PE的长,从而得出ED的长,最后根据正切函数的定义即可算出答案。
10.答案:C
解析:解:如图,
依题意得AB=6,CD=8,过O点作AB的垂线,垂足为E,交CD于F点,连接OA,OC,由垂径定理,得AE= AB=3,CF= CD=4,
设OE=x,则OF=x﹣1,
在Rt△OAE中,OA2=AE2+OE2,
在Rt△OCF中,OC2=CF2+OF2,
∵OA=OC,
∴32+x2=42+(x﹣1)2,
解得x=4,
∴半径OA= =5,
∴直径MN=2OA=10分米.
故答案为:C.
分析:过O点作AB的垂线,垂足为E,交CD于F点,连接OA、OC,由垂径定理可知AE= AB=3、CF=CD=4,设OE=x,在Rt△OAE和Rt△OCF中,利用斜边相等借助勾股定理列出x的方程,据此即可解答。
11.答案:B
解析:解:如图:连接OA、OD,作OE⊥AC于E,OF⊥BD于F,
∵AC⊥BD,
∴四边形OEPF为矩形,
∵OA=OD=2,OP= ,
设OE为x(x>0),
根据勾股定理得,OF=EP= = ,
在Rt△AOE中,AE= =
∴AC=2AE=2 ,
同理得,BD=2DF=2 =2 ,
又∵任意对角线互相垂直的四边形的面积等于对角线乘积的 ,
∴S四边形ABCD= AC×BD= ×2 ×2 =2 =2
当x2= 即:x= 时,四边形ABCD的面积最大,等于2 =5.
答案为:B.
分析:作出弦心距,根据S四边形ABCD=对角线乘积的一半,列出函数关系式,配成顶点式,求出最值.
12.答案:C
解析:解:∵AB=10,
∵OB=OA=OC=5,
过E作CD⊥AB于E,连接OC,则CD是过E的⊙O的最短的弦,
∵OB⊥CD,
∴∠CEO=90°,
由勾股定理得:CE= = =3,
∵OE⊥CD,OE过O,
∴CD=2CE=6,
∵AB是过E的⊙O的最长弦,AB=10,
∴过E点所有弦中,长度为整数的条数为1+2+2+2+1=8,
答案为:C.
分析:求出过E的最短的弦,就是以OE为弦心距的弦,最长的弦就是直径,在这个范围内取整数,注意对称性.
13.答案:这条弦;弦所对的弧
解析: 垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的弧,这里的“弧"包括弦所对的两条弧.
故答案为:这条弦 , 弦所对的弧.
分析:根据垂径定理填空即可.
14.答案:
解析:据垂径定理和股定理可以求的弦长为6 .
分析:此题考查了垂径定理和勾股定理知识点.
15.答案:;;
解析:解:∵AB是圆O的直径,且AB⊥CD,
∴CE=DE,,.
故答案为:CE=DE,,.
分析:由垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的弧可直接得出答案.
16.答案:②④
解析:解:①因为平分弧的直径一定垂直于弦,所以一定平分弧所对的弦;故①正确;
②因为平分弦(不是直径)的直径平分弦所对的弧;故②错误;
③因为平分弦的直径垂直于弦,所以垂直平分弦的直线必经过圆心,故③正确;
④因为平分弦(非直径)的直径一定垂直于弦,故④错误;
故答案为:②④.
分析:根据垂直于弦的直径平分这条弦,并且平分弦所对的两条弧;平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;弦的垂直平分线经过圆心,并且平分弦所对的两条弧;平分弦所对一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧进行分析即可得出答案.
17.答案:25
解析:解:设脸盆所在圆的圆心为O,连接OC交AB于点D,连接OA,如图:
∴
设脸盆的半径为xcm,则
在中,
即
解得:
则该脸盆的半径为25cm.
故答案为:25.
分析:设圆心为O,连接OC交AB于点D,连接OA,根据垂径定理得AD=BD=AB=20cm,设脸盆的半径为xcm,则OD=(x-10)cm,在Rt△AOD中,根据勾股定理列方程,解方程即可求解.
18.答案:解:过O作OE⊥AB于点E,
则CE=DE,AE=BE,
∴BE-DE=AE-CE.
即AC=BD.
解析:过O作OE⊥AB于点E,根据垂径定理可知CE=DE、AE=BE,利用等式性质即可证明。
19.答案:解:过点O作OM⊥DE于点M,连接OD.
∴DM= .
∵DE=8(cm)
∴DM=4(cm)
在Rt△ODM中,∵OD=OC=5(cm),
∴OM= = =3(cm)
∴直尺的宽度为3cm.
解析:过点O作OM⊥DE于点M,连接OD,由垂径定理可知DM= DE=4,在Rt△ODM中借助勾股定理即可解答。
20.答案:解:过E作EF⊥AB于F,EG⊥CD于G,连接EB,CE,DE,如图:
∵A、B的坐标分别为(-2,0)、(4,0),
∴AB=6,OB=4,
∵EF⊥AB,
∴,
∴OF=1,
∵⊙E的直径为10,
∴半径EB=5,
∴,
∴E的坐标是(1,-4).
则EG=1,
∴,
则
∴点C的坐标是,
则
点D的坐标是.
解析:过E作EF⊥AB于F,EG⊥CD于G,连接EB,CE,DE,先根据A、B点的坐标求出AB的长,再根据垂径定理求出BF的长,即可求出OF的长,再利用直角三角形中两直角边的平方和等于斜边的平方求出EF的值,得出E点坐标,再利用直角三角形中两直角边的平方和等于斜边的平方求出CG的值,即可求出点C和点D的坐标.
21.答案:(1)解: 连接OA,如图:
由题意得:(米),OD=(r-18)米,
在Rt△ADO中,由勾股定理得:r2=302+(r-18)2,
解得:r=34(米);
即OP=34m.
(2)解: 连接OA′,
∵OE=OP-PE=30米,
∴在Rt△A′EO中,由勾股定理得:A′E2=A′O2-OE2,即:A′E2=342-302,
解得:A′E=16(米).
∴A′B′=32(米).
∵A′B′=32>30,
∴不需要采取紧急措施.
解析:(1)连接OA,利用r表示出OP的长,在Rt△AOD中,根据直角三角形中两直角边的平方和等于斜边的平方求出r的值即可;
(2)连接OA′,在Rt△A′EO中,由直角三角形中两直角边的平方和等于斜边的平方得出A′E的长,进而可得出A′B′的长,据此可得出结论.
22.答案:(1)解:∵OD⊥BC,
∴BD=BC= ×6=3,
∵∠BDO= 90°,OB=5,BD=3,
OD= =4,
即线段OD的长为4;
(2)解:如图,连结AB,DE,
∵∠AOB=90° ,OA=OB=5,
∴AB= .
∵OD⊥BC,OE⊥AC,
∴D,E分别是线段BC,AC的中点,
∴DE是△ABC的中位线,
∴DE=AB= ;
(3)解:∠DOE的度数不变,为45°,理由如下:
设OD交弧BC于点M,OE交弧AC于点N,
∵
∴
∴
∵
∴
即
解析:(1)根据垂径定理得到BD=BC,在Rt△BDO中利用勾股定理即可求出OD的长;
(2)连结AB,在Rt△AOB中,利用勾股定理求出AB的长,由垂径定理得D,E分别是线段BC,AC的中点,最后根据三角形中位线定理即可求出DE的长;
(3)∠DOE的度数不变,为45°,理由如下:根据垂径定理即可求得,进而根据圆心角、弧、弦的关系可求出∠DOE的度数.
将来的某一天,你会感谢曾经努力的自己!
