2023-2024学年北师大版九年级下册同步练习【提升卷】2.4二次函数的运用同步练习(含解析)
文档属性
| 名称 | 2023-2024学年北师大版九年级下册同步练习【提升卷】2.4二次函数的运用同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 500.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-19 00:00:00 | ||
图片预览




文档简介
2023-2024学年北师大版九年级下册同步练习【提升卷】
2.4二次函数的运用 同步练习
班级: 姓名:
一、选择题
1.用绳子围成周长为10(m)的矩形,记矩形的一边长为x(m),面积为S(m2).当x在一定范围内变化时,S随x的变化而变化,则S与x满足的函数关系是( )
A.一次函数关系 B.二次函数关系
C.反比例函数关系 D.正比例函数关系
2.如图所示是一个抛物线形桥拱的示意图,在所给出的平面直角坐标系中,当水位在AB位置时,水面宽度为10m,此时水面到桥拱的距离是4m,则抛物线的函数关系式为( )
A.y= B.y=﹣ C.y=﹣ D.y=
3.如图,某校的围墙由一段相同的凹曲拱组成,其拱状图形为抛物线的一部分,栅栏的跨径AB以相同间隔0.2米用5根立柱加固,拱高OC为0.36米,则立柱EF的长为( )
A.0.4米 B.0.16米 C.0.2米 D.0.24米
4.图(1)是一个横断面为抛物线形状的拱桥,当水面在l时,拱顶(拱桥洞的最高点)离水面2m,水面宽4m.如图(2)建立平面直角坐标系,则抛物线的关系式是( )
A.y=﹣2x2 B.y=2x2 C.y=﹣ x2 D.y= x2
5.某公司的生产利润原来是a元,经过连续两年的增长达到了y万元,如果每年增长的百分数都是x,那么y与x的函数关系是( )
A.y=x2+a B.y=a(x﹣1)2
C.y=a(1﹣x)2 D.y=a(1+x)2
6.一件工艺品的进价为100元,标价135元出售,每天可售出100件,根据销售统计,一件工艺品每降价1元,则每天可多售出4件,要使每天获得的利润最大,则每件需降价( )
A.3.6 元 B.5 元 C.10 元 D.12 元
7.如图,排球运动员站在点O处练习发球,将球从O点正上方2m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x﹣k)2+h.已知球与O点的水平距离为6m时,达到最高2.6m,球网与O点的水平距离为9m.高度为2.43m,球场的边界距O点的水平距离为18m,则下列判断正确的是( )
A.球不会过网 B.球会过球网但不会出界
C.球会过球网并会出界 D.无法确定
8.足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度h(单位:m)与足球被踢出后经过的时间t(单位:s)之间的关系如下表:
t 0 1 2 3 4 5 6 7 …
h 0 8 14 18 20 20 18 14 …
下列结论:①足球距离地面的最大高度为20m;②足球飞行路线的对称轴是直线t= ;③足球被踢出9s时落地;④足球被踢出1.5s时,距离地面的高度是11m.其中正确结论的个数是( )
A.1 B.2 C.3 D.4
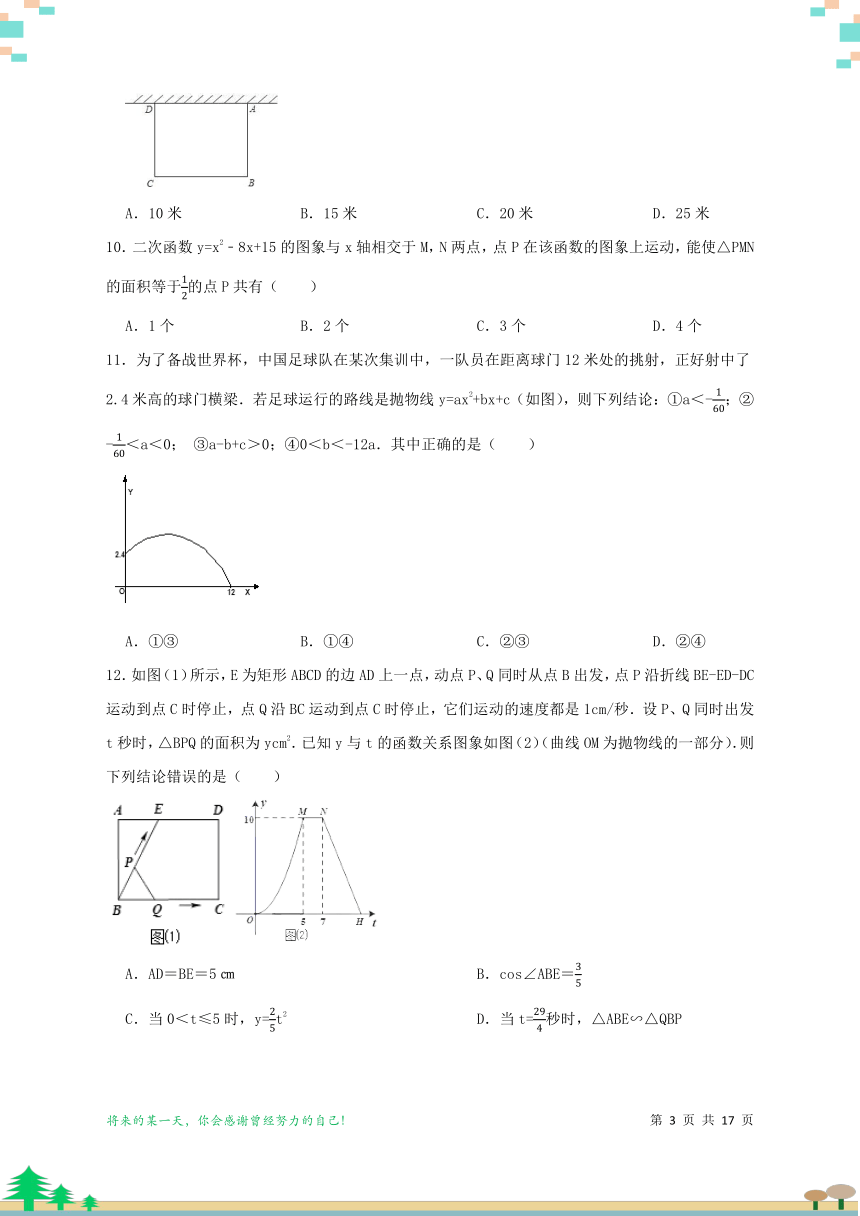
9.如图,一边靠校园围墙,其他三边用总长为40米的铁栏杆围成一个矩形花圃,设矩形ABCD的边AB为x米,面积为S平方米,要使矩形ABCD面积最大,则x的长为( )
A.10米 B.15米 C.20米 D.25米
10.二次函数y=x2﹣8x+15的图象与x轴相交于M,N两点,点P在该函数的图象上运动,能使△PMN的面积等于的点P共有( )
A.1个 B.2个 C.3个 D.4个
11.为了备战世界杯,中国足球队在某次集训中,一队员在距离球门12米处的挑射,正好射中了2.4米高的球门横梁.若足球运行的路线是抛物线y=ax2+bx+c(如图),则下列结论:①a<-;②-<a<0; ③a-b+c>0;④0<b<-12a.其中正确的是( )
A.①③ B.①④ C.②③ D.②④
12.如图(1)所示,E为矩形ABCD的边AD上一点,动点P、Q同时从点B出发,点P沿折线BE-ED-DC运动到点C时停止,点Q沿BC运动到点C时停止,它们运动的速度都是1cm/秒.设P、Q同时出发t秒时,△BPQ的面积为ycm2.已知y与t的函数关系图象如图(2)(曲线OM为抛物线的一部分).则下列结论错误的是( )
A.AD=BE=5㎝ B.cos∠ABE=
C.当0<t≤5时,y=t2 D.当t=秒时,△ABE∽△QBP
二、填空题
13.(2021九下·广州开学考)教练对小明推铅球的录像进行技术分析,发现铅球行进高度 与水平距离 之间的关系为 ,由此可知铅球推出的距离是 m.
14.某企业今年第一月新产品的研发资金为100万元,以后每月新产品的研发资金与上月相比增长的都是x,则该厂今年第三月新产品的研发资金y(元)关于x的函数关系式为y= .
15.如图,四边形ABCD是矩形,A、B两点在x轴的正半轴上,C、D两点在抛物线y=﹣x2+6x上.设OA=m(0<m<3),矩形ABCD的周长为l,则l与m的函数解析式为 .
16.已知抛物线y=x2﹣k的顶点为P,与x轴交于点A,B,且△ABP是正三角形,则k的值是 .
17.某种工艺品利润为60元/件,现降价销售,该种工艺品销售总利润w(元)与降价x(元)的函数关系如图.这种工艺品的销售量为 件(用含x的代数式表示).
三、解答题
18.为了改善小区环境,某小区决定要在一块一边靠墙(墙长25m)的空地上修建一条矩形绿化带ABCD,绿化带一边靠墙,另三边用总长为40m的栅栏围住(如图).若设绿化带BC边长为xm,绿化带的面积为ym2,求y与x之间的函数关系式,并写出自变量x的取值范围.
某公园门票每张是80元,据统计每天进园人数为200人,经市场调查发现,如果门票每降低1元出售,则每天进园人数就增多6人,试写出门票价格为x(x≤80)元时,该公园每天的门票收入y(元),y是x的二次函数吗?
用总长为L米的篱笆围成长方形场地,已知长方形的面积为60m2,一边长度x米,求L与x之间的关系式,并写出自变量x的取值范围.
21.一家图文广告公司制作的宣传画板颇受商家欢迎,这种画板的厚度忽略不计,形状均为正方形,边长在10~30dm之间.每张画板的成本价(单位:元)与它的面积(单位:dm2)成正比例,每张画板的出售价(单位:元)由基础价和浮动价两部分组成,其中基础价与画板的大小无关,是固定不变的.浮动价与画板的边长成正比例.在营销过程中得到了表格中的数据.
画板的边长(dm) 10 20
出售价(元/张) 160 220
求一张画板的出售价与边长之间满足的函数关系式;
(2)已知出售一张边长为30dm的画板,获得的利润为130元(利润=出售价-成本价),
①求一张画板的利润与边长之间满足的函数关系式;
②当边长为多少时,出售一张画板所获得的利润最大?最大利润是多少?
22.如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,B点的坐标为(3,0),与y轴交于点C(0,﹣3),点P是直线BC下方抛物线上的任意一点.
(1)求这个二次函数y=x2+bx+c的解析式.
(2)连接PO,PC,并将△POC沿y轴对折,得到四边形POP′C,如果四边形POP′C为菱形,求点P的坐标.
(3)如果点P在运动过程中,能使得以P、C、B为顶点的三角形与△AOC相似,请求出此时点P的坐标.
答案解析部分
1.答案:B
解析:解:∵矩形周长为10 m,一边长为x m,
∴另一边长为:(10-2x)÷2=5-x (m),
∴S=x(5-x)=-x2+5x.
故答案为:B.
分析:结合矩形对边相等,将另一边长表示出来,再根据面积=长×宽,建立出S与x的关系式,即可判断.
2.答案:C
解析:解:依题意设抛物线解析式y=ax2,
把B(5,﹣4)代入解析式,
得﹣4=a×52,
解得a=﹣ ,
所以y=﹣ x2.
故答案为:C.
分析:由题意可设抛物线解析式y=ax2,因为点B(5,﹣4),所以将点B(5,﹣4)代入解析式计算即可求解。
3.答案:C
解析:由于相同的间距0.2m用5根立柱加固,则AB=0.2×6=1.2,以C坐标系的原点,OC所在直线为y轴建立坐标系,由此得到抛物线过(0.6,0.36)、(0,0)、(-0.6,0.36),据此求出解析式.把x=-0.4代入后求出y,让0.36-y即可.
解:如图,以C坐标系的原点,OC所在直线为y轴建立坐标系,
设抛物线解析式为y=ax2,
由题知,图象过B(0.6,0.36),
代入得:0.36=0.36a
∴a=1,即y=x2.
∵F点横坐标为-0.4,
∴当x=-0.4时,y=0.16,
∴EF=0.36-0.16=0.2米
故选C.
点评:本题考查点的坐标的求法及二次函数的实际应用.此题为数学建模题,借助二次函数解决实际问题
4.答案:C
解析:解:设此函数解析式为:y=ax2,a≠0;
那么(2,﹣2)应在此函数解析式上.
则﹣2=4a
即得a=﹣ ,
那么y=﹣ x2.
故答案为:C.
分析:观察函数图象可知:抛物线的顶点在原点,对称轴为y轴,图象经过(2,-2),因此设函数解析式为y=ax2,利用待定系数法就可求出结果。
5.答案:D
解析:解:依题意,
得y=a(1+x)2.
故答案为:D.
分析:由两年后的利润y=两年前的利润×(1+增长率)2,代入相关数据,就可得出y与x的函数解析式。
6.答案:B
解析:解:设每件降价x元,每天获得的利润记为W,
根据题意,W=(135﹣x﹣100)(100+4x)
=﹣4x2+40x+3500
=﹣4(x﹣5)2+3600,
∵﹣4<0,
∴当x=5时,W取得最大值,最大值为3600,
即每件降价5元时,每天获得的利润最大,最大利润为3600元.
故答案为:B.
分析:根据降价后 :利润w=月销售量每件的利润,建立函数解析式,再求出顶点坐标,根据二次函数的性质即可得出答案。
7.答案:C
解析:解:(1)∵球与O点的水平距离为6m时,达到最高2.6m,
∴抛物线为y=a(x﹣6)2+2.6过点,
∵抛物线y=a(x﹣6)2+2.6过点(0,2),
∴2=a(0﹣6)2+2.6,
解得:a=﹣ ,
故y与x的关系式为:y=﹣ (x﹣6)2+2.6,
当x=9时,y=﹣ (x﹣6)2+2.6=2.45>2.43,
所以球能过球网;
当y=0时,﹣ (x﹣6)2+2.6=0,
解得:x1=6+2 >18,x2=6﹣2 (舍去)
故会出界.
故答案为:C.
分析:先根据题意列出y与x的函数解析式,再将x=9代入函数解析式求出y的值,可得出球能过球网,再根据y=0求出对应的自变量的值,再与18 比较大小,即可得出答案。
8.答案:B
解析:解:由题意,抛物线的解析式为y=at(t﹣9),把(1,8)代入可得a=﹣1,
∴y=﹣t2+9t=﹣(t﹣4.5)2+20.25,
∴足球距离地面的最大高度为20.25m,故①错误,
∴抛物线的对称轴t=4.5,故②正确,
∵t=9时,y=0,
∴足球被踢出9s时落地,故③正确,
∵t=1.5时,y=11.25,故④错误.
∴正确的有②③,
故答案为:B.
分析:根据题意,抛物线的解析式为y=at(t﹣9),把(1,8)代入求出a的值,得出函数解析式,再将函数解析式化成顶点式,即可对各选项一一判断即可。
9.答案:A
解析:设矩形ABCD的边AB为x米,则宽为40-2x,
S=(40-2x)x= -2x2+40x.
要使矩形ABCD面积最大,
则
即x的长为10m.
故选A.
分析:求二次函数的最大(小)值有三种方法,第一种可由图象直接得出,第二种是配方法,第三种是公式法,常用的是后两种方法,当二次系数a的绝对值是较小的整数时,用配方法较好,如y= -x2-2x+5,y=3x2-6x+1等用配方法求解比较简单.
10.答案:D
解析:解:y=x2﹣8x+15的图象与x轴交点(3,0)和(5,0),
|MN|=2,
设p点(x,y),
y=x2﹣8x+15,
面积==|MN| |y|,
可得y1=,或者y2=﹣
当y=时,x=;
当y=﹣时,x=
所以共有四个点.
故选D.
分析:由题可求出MN的长,即△MNP的底边已知,要求面积为,那么根据面积即可求出高,只要把相应的y值代入即可解答.
11.答案:B
解析:由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断。
解:由抛物线的开口向下知a<0
对称轴为,
∴a、b异号,即b>0.
与y轴的交点坐标为(0,2.4),
∴c=2.4.
把点(12,0)代入解析式得,144a+12b+2.4=0
∴144a=-2.4-12b,12b=-2.4-144a,
∴144a+12b=-2.12b+2.4<144a,
∴144a<-2.4,12b<-144a
∴a<,b<-12a
∴①④正确,②错误,
∵此题是实际问题,
∴x≥0,
∴③a-b+c>0错误.
故选B.
点评:解决此类题目要熟练掌握二次函数的图象和性质,解题的关键是注意数形结合思想的应用。
12.答案:B
解析:根据图(2)可以判断三角形的面积变化分为三段,可以判断出当点P到达点E时点Q到达点C,从而得到BC、BE的长度,再根据M、N是从5秒到7秒,可得ED的长度,然后表示出AE的长度,根据勾股定理求出AB的长度,然后针对各小题分析解答即可.
解:根据图(2)可得,当点P到达点E时点Q到达点C,
∵点P、Q的运动的速度都是1cm/秒,
∴BC=BE=5,
∴AD=BE=5,故A正确;
又∵从M到N的变化是2,
∴ED=2,
∴AE=AD-ED=5-2=3,
在Rt△ABE中,
∴cos∠ABE==,故B错误;
如图(1)过点P作PF⊥BC于点F,
∵AD∥BC,
∴∠AEB=∠PBF,
∴sin∠PBF=sin∠AEB==
∴PF=PBsin∠PBF=t,
∴当0<t≤5时,y=BQ PF=t t=t2,故C正确;
当t=秒时,点P在CD上,此时,PD=-BE-ED=-5-2=,
PQ=CD-PD=4-=,
∵=,=,
∴=,
又∵∠A=∠Q=90°,
∴△ABE∽△QBP,故D正确.
由于该题选择错误的,故选:B.
点评:本题考查了动点问题的函数图象,根据图(2)判断出点P到达点E时点Q到达点C是解题的关键,也是本题的突破口
13.答案:11
解析:解:根据题意可知 ,
则 ,
解得 , ,
∵ ,
∴ ,
故铅球推出的距离是11米.
故答案为:11.
分析:根据铅球落地时,高度y=0,把实际问题可理解为当y=0时,求x的值即可.
14.答案:100(1+x)2
解析:解:∵一月份新产品的研发资金为100元,
2月份起,每月新产品的研发资金与上月相比增长率都是x,
∴2月份研发资金为100(1+x),
∴三月份的研发资金为y=100(1+x)×(1+x)=100(1+x)2.
故答案为:100(1+x)2.
分析:根据三月份的研发资金为y=一月份的研发资金×(1+增长率)2,就可得出结果。
15.答案:l=﹣2m2+8m+12
解析:解: 把x=m代入抛物线y=﹣x 2+6x中,得AD=﹣m 2+6m
把y=﹣m2+6m代入抛物线y=﹣x2+6x中,得
﹣m2+6m=﹣x2+6x
解得x1=m,x2=6﹣m
∴C的横坐标是6﹣m,故AB=6﹣m﹣m=6﹣2m
∴矩形的周长是l=2(﹣m2+6m)+2(6﹣2m)
即l=﹣2m2+8m+12.
分析:因为矩形的周长l=2(AB+AD),要求周长,只需求得AB和AD的长即可。由矩形的性质和已知条件可知,点A、D的横坐标相同,点C、D的纵坐标相同,所以只需把x=m代入解析式可得点D的纵坐标,把点D的纵坐标代入解析式可求得点C的横坐标,于是线段AB和AD的长可求解,则 l与m的函数解析式 可求解。
16.答案:3
解析:解:如图,
∵抛物线y=x2﹣k的顶点为P,
∴P点的坐标为:(0,﹣k),
∴PO=k,
∵抛物线y=x2﹣k与x轴交于A、B两点,且△ABP是正三角形,
∴OA=OB,∠OPB=30°,
∴tan30°= = ,
∴OB= k,
∴点B的坐标为:( k,0),点B在抛物线y=x2﹣k上,
∴将B点代入y=x2﹣k,得:
0=( k)2﹣k,
整理得: ﹣k=0,
解得:k1=0(不合题意舍去),k2=3.
故答案为:3.
分析:先求出抛物线的顶点P的坐标,得出OP的长,再由 △ABP是正三角形,利用解直角三角形求出OB的值,就可得出点B的坐标,然后将点B的坐标代入函数解析式,就可求出k的值。
17.答案:(60+x)
解析:解:由函数的图象可知点(30,2700)和点(60,0)满足解析式w=mx2+n,
∴ ,
解得: ,
∴w=﹣x2+3600,
设销售量为a,则a(60﹣x)=w,
即a(60﹣x)=﹣x2+3600,
解得:a=60+x ,
故答案为:60+x.
分析:由函数的图象可知点(30,2700)和点(60,0)满足解析式w=mx2+n,可求出w与x的关系式,设销售量为a,则每件工艺品的利润 为(60﹣x)元,根据总利润=每件工艺品的利润×销售量,列式整理即可求出。
18.答案:解:由题意得:y=x× =﹣ x2+20x,自变量x的取值范围是0<x≤25.
解析:由长方形的性质可将AB表示成AB=
,则长方形的面积=长
× 宽=AB
× BC;易得
自变量x的取值范围是0<x≤25.
19.答案:解:根据题意可得:
y=x[200+6(80﹣x)]
=﹣6x2+680x.
解析: 该公园每天的门票收入y=门票的单价×每天进园的人数,列出函数解析式即可。
20.答案:解:∵用总长为L米的篱笆围成长方形场地,一边长度x米,
∴另一边长为:( ﹣x)m,
故x( ﹣x)=60,
则L= +2x,(0<x< ).
解析:根据长方形的周长表示出长方形的另一边,再利用长方形的面积=长×宽,就可得出L与x的函数解析式,然后求出x的取值范围。
21.答案:(1)设正方形画板的边长为xdm,出售价为每张y元,且y=kx+b(k≠0) (1分)
由表格中的数据可得,,解得
从而一张画板的出售价y与边长x之间满足函数关系式y=6x+100
(2)设每张画板的成本价为ax2,利润W=6x+100-ax2
当x=30时,W=130,180+100-900a=130,得a=
一张画板的利润W与边长x之间满足函数关系式W=-x2+6x+100
由W=-16(x-18)2+154,知当x=18时,W有最大值,W最大=154
因此当正方形画板的边长为18dm时,可获最大利润154元.
解析:(1)每张画板的成本价与它的面积成正比例,可设其解析式为y成本价=ax2,每张画板的出售价由基础价和浮动价两部分组成,其中基础价与画板的大小无关,是固定不变的.浮动价与画板的边长成正比例.可设y出售价=kx+b.把表中数据代入即可求出结论;
(2)由y利润=y出售价-y成本价,可得出二次函数,求出其最大值即可.
22.答案:解:(1)将B、C点代入函数解析式,得
,
解得,
这个二次函数y=x2+bx+c的解析式为y=x2﹣2x﹣3;
(2)四边形POP′C为菱形,得
OC与PP′互相垂直平分,得
yP=,即x2﹣2x﹣3=﹣,
解得x1=,x2=(舍),P(,﹣);
(3)∠PBC<90°,
①如图1
当∠PCB=90°时,过P作PH⊥y轴于点H,
BC的解析式为y=x﹣3,CP的解析式为y=﹣x﹣3,
设点P的坐标为(m,﹣3﹣m),
将点P代入代入y═x2﹣2x﹣3中,
解得m1=0(舍),m2=1,即P(1,﹣4);
AO=1,OC=3,CB==3,CP==,
此时=3,△AOC∽△PCB;
②如图2
,
当∠BPC=90°时,作PH⊥y轴于H,作BD⊥PH于D,
BC的解析式为y=x﹣3,CP的解析式为y=x﹣3,
设点P的坐标为(m,m2﹣2m﹣3),
由Kcp Kpb=﹣1,得m=或(舍去)
此时,==≠=3,
以P、C、B为顶点的三角形与△AOC不相似;
综上所述:P、C、B为顶点的三角形与△AOC相似,此时点P的坐标(1,﹣4).
解析:(1)根据待定系数法,可得函数解析式;
(2)根据菱形的对角线互相垂直平分,可得P点的纵坐标,根据自变量与函数值的对应关系,可得答案;
(3)分类讨论:①当∠PCB=90°,根据互相垂直的两条直线的一次项系数互为负倒数,可得BP的解析式,根据自变量与函数值的对应关系,可得P点坐标;根据勾股定理,可得BC,CP的长,根据两组对边对应成比例且夹角相等的两个三角形相似,可得答案;
②当∠BPC=90°时,根据相似三角形的性质,可得P点的坐标,根据两组对边对应成比例且夹角相等的两个三角形相似,可得答案.
将来的某一天,你会感谢曾经努力的自己!
2.4二次函数的运用 同步练习
班级: 姓名:
一、选择题
1.用绳子围成周长为10(m)的矩形,记矩形的一边长为x(m),面积为S(m2).当x在一定范围内变化时,S随x的变化而变化,则S与x满足的函数关系是( )
A.一次函数关系 B.二次函数关系
C.反比例函数关系 D.正比例函数关系
2.如图所示是一个抛物线形桥拱的示意图,在所给出的平面直角坐标系中,当水位在AB位置时,水面宽度为10m,此时水面到桥拱的距离是4m,则抛物线的函数关系式为( )
A.y= B.y=﹣ C.y=﹣ D.y=
3.如图,某校的围墙由一段相同的凹曲拱组成,其拱状图形为抛物线的一部分,栅栏的跨径AB以相同间隔0.2米用5根立柱加固,拱高OC为0.36米,则立柱EF的长为( )
A.0.4米 B.0.16米 C.0.2米 D.0.24米
4.图(1)是一个横断面为抛物线形状的拱桥,当水面在l时,拱顶(拱桥洞的最高点)离水面2m,水面宽4m.如图(2)建立平面直角坐标系,则抛物线的关系式是( )
A.y=﹣2x2 B.y=2x2 C.y=﹣ x2 D.y= x2
5.某公司的生产利润原来是a元,经过连续两年的增长达到了y万元,如果每年增长的百分数都是x,那么y与x的函数关系是( )
A.y=x2+a B.y=a(x﹣1)2
C.y=a(1﹣x)2 D.y=a(1+x)2
6.一件工艺品的进价为100元,标价135元出售,每天可售出100件,根据销售统计,一件工艺品每降价1元,则每天可多售出4件,要使每天获得的利润最大,则每件需降价( )
A.3.6 元 B.5 元 C.10 元 D.12 元
7.如图,排球运动员站在点O处练习发球,将球从O点正上方2m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x﹣k)2+h.已知球与O点的水平距离为6m时,达到最高2.6m,球网与O点的水平距离为9m.高度为2.43m,球场的边界距O点的水平距离为18m,则下列判断正确的是( )
A.球不会过网 B.球会过球网但不会出界
C.球会过球网并会出界 D.无法确定
8.足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度h(单位:m)与足球被踢出后经过的时间t(单位:s)之间的关系如下表:
t 0 1 2 3 4 5 6 7 …
h 0 8 14 18 20 20 18 14 …
下列结论:①足球距离地面的最大高度为20m;②足球飞行路线的对称轴是直线t= ;③足球被踢出9s时落地;④足球被踢出1.5s时,距离地面的高度是11m.其中正确结论的个数是( )
A.1 B.2 C.3 D.4
9.如图,一边靠校园围墙,其他三边用总长为40米的铁栏杆围成一个矩形花圃,设矩形ABCD的边AB为x米,面积为S平方米,要使矩形ABCD面积最大,则x的长为( )
A.10米 B.15米 C.20米 D.25米
10.二次函数y=x2﹣8x+15的图象与x轴相交于M,N两点,点P在该函数的图象上运动,能使△PMN的面积等于的点P共有( )
A.1个 B.2个 C.3个 D.4个
11.为了备战世界杯,中国足球队在某次集训中,一队员在距离球门12米处的挑射,正好射中了2.4米高的球门横梁.若足球运行的路线是抛物线y=ax2+bx+c(如图),则下列结论:①a<-;②-<a<0; ③a-b+c>0;④0<b<-12a.其中正确的是( )
A.①③ B.①④ C.②③ D.②④
12.如图(1)所示,E为矩形ABCD的边AD上一点,动点P、Q同时从点B出发,点P沿折线BE-ED-DC运动到点C时停止,点Q沿BC运动到点C时停止,它们运动的速度都是1cm/秒.设P、Q同时出发t秒时,△BPQ的面积为ycm2.已知y与t的函数关系图象如图(2)(曲线OM为抛物线的一部分).则下列结论错误的是( )
A.AD=BE=5㎝ B.cos∠ABE=
C.当0<t≤5时,y=t2 D.当t=秒时,△ABE∽△QBP
二、填空题
13.(2021九下·广州开学考)教练对小明推铅球的录像进行技术分析,发现铅球行进高度 与水平距离 之间的关系为 ,由此可知铅球推出的距离是 m.
14.某企业今年第一月新产品的研发资金为100万元,以后每月新产品的研发资金与上月相比增长的都是x,则该厂今年第三月新产品的研发资金y(元)关于x的函数关系式为y= .
15.如图,四边形ABCD是矩形,A、B两点在x轴的正半轴上,C、D两点在抛物线y=﹣x2+6x上.设OA=m(0<m<3),矩形ABCD的周长为l,则l与m的函数解析式为 .
16.已知抛物线y=x2﹣k的顶点为P,与x轴交于点A,B,且△ABP是正三角形,则k的值是 .
17.某种工艺品利润为60元/件,现降价销售,该种工艺品销售总利润w(元)与降价x(元)的函数关系如图.这种工艺品的销售量为 件(用含x的代数式表示).
三、解答题
18.为了改善小区环境,某小区决定要在一块一边靠墙(墙长25m)的空地上修建一条矩形绿化带ABCD,绿化带一边靠墙,另三边用总长为40m的栅栏围住(如图).若设绿化带BC边长为xm,绿化带的面积为ym2,求y与x之间的函数关系式,并写出自变量x的取值范围.
某公园门票每张是80元,据统计每天进园人数为200人,经市场调查发现,如果门票每降低1元出售,则每天进园人数就增多6人,试写出门票价格为x(x≤80)元时,该公园每天的门票收入y(元),y是x的二次函数吗?
用总长为L米的篱笆围成长方形场地,已知长方形的面积为60m2,一边长度x米,求L与x之间的关系式,并写出自变量x的取值范围.
21.一家图文广告公司制作的宣传画板颇受商家欢迎,这种画板的厚度忽略不计,形状均为正方形,边长在10~30dm之间.每张画板的成本价(单位:元)与它的面积(单位:dm2)成正比例,每张画板的出售价(单位:元)由基础价和浮动价两部分组成,其中基础价与画板的大小无关,是固定不变的.浮动价与画板的边长成正比例.在营销过程中得到了表格中的数据.
画板的边长(dm) 10 20
出售价(元/张) 160 220
求一张画板的出售价与边长之间满足的函数关系式;
(2)已知出售一张边长为30dm的画板,获得的利润为130元(利润=出售价-成本价),
①求一张画板的利润与边长之间满足的函数关系式;
②当边长为多少时,出售一张画板所获得的利润最大?最大利润是多少?
22.如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,B点的坐标为(3,0),与y轴交于点C(0,﹣3),点P是直线BC下方抛物线上的任意一点.
(1)求这个二次函数y=x2+bx+c的解析式.
(2)连接PO,PC,并将△POC沿y轴对折,得到四边形POP′C,如果四边形POP′C为菱形,求点P的坐标.
(3)如果点P在运动过程中,能使得以P、C、B为顶点的三角形与△AOC相似,请求出此时点P的坐标.
答案解析部分
1.答案:B
解析:解:∵矩形周长为10 m,一边长为x m,
∴另一边长为:(10-2x)÷2=5-x (m),
∴S=x(5-x)=-x2+5x.
故答案为:B.
分析:结合矩形对边相等,将另一边长表示出来,再根据面积=长×宽,建立出S与x的关系式,即可判断.
2.答案:C
解析:解:依题意设抛物线解析式y=ax2,
把B(5,﹣4)代入解析式,
得﹣4=a×52,
解得a=﹣ ,
所以y=﹣ x2.
故答案为:C.
分析:由题意可设抛物线解析式y=ax2,因为点B(5,﹣4),所以将点B(5,﹣4)代入解析式计算即可求解。
3.答案:C
解析:由于相同的间距0.2m用5根立柱加固,则AB=0.2×6=1.2,以C坐标系的原点,OC所在直线为y轴建立坐标系,由此得到抛物线过(0.6,0.36)、(0,0)、(-0.6,0.36),据此求出解析式.把x=-0.4代入后求出y,让0.36-y即可.
解:如图,以C坐标系的原点,OC所在直线为y轴建立坐标系,
设抛物线解析式为y=ax2,
由题知,图象过B(0.6,0.36),
代入得:0.36=0.36a
∴a=1,即y=x2.
∵F点横坐标为-0.4,
∴当x=-0.4时,y=0.16,
∴EF=0.36-0.16=0.2米
故选C.
点评:本题考查点的坐标的求法及二次函数的实际应用.此题为数学建模题,借助二次函数解决实际问题
4.答案:C
解析:解:设此函数解析式为:y=ax2,a≠0;
那么(2,﹣2)应在此函数解析式上.
则﹣2=4a
即得a=﹣ ,
那么y=﹣ x2.
故答案为:C.
分析:观察函数图象可知:抛物线的顶点在原点,对称轴为y轴,图象经过(2,-2),因此设函数解析式为y=ax2,利用待定系数法就可求出结果。
5.答案:D
解析:解:依题意,
得y=a(1+x)2.
故答案为:D.
分析:由两年后的利润y=两年前的利润×(1+增长率)2,代入相关数据,就可得出y与x的函数解析式。
6.答案:B
解析:解:设每件降价x元,每天获得的利润记为W,
根据题意,W=(135﹣x﹣100)(100+4x)
=﹣4x2+40x+3500
=﹣4(x﹣5)2+3600,
∵﹣4<0,
∴当x=5时,W取得最大值,最大值为3600,
即每件降价5元时,每天获得的利润最大,最大利润为3600元.
故答案为:B.
分析:根据降价后 :利润w=月销售量每件的利润,建立函数解析式,再求出顶点坐标,根据二次函数的性质即可得出答案。
7.答案:C
解析:解:(1)∵球与O点的水平距离为6m时,达到最高2.6m,
∴抛物线为y=a(x﹣6)2+2.6过点,
∵抛物线y=a(x﹣6)2+2.6过点(0,2),
∴2=a(0﹣6)2+2.6,
解得:a=﹣ ,
故y与x的关系式为:y=﹣ (x﹣6)2+2.6,
当x=9时,y=﹣ (x﹣6)2+2.6=2.45>2.43,
所以球能过球网;
当y=0时,﹣ (x﹣6)2+2.6=0,
解得:x1=6+2 >18,x2=6﹣2 (舍去)
故会出界.
故答案为:C.
分析:先根据题意列出y与x的函数解析式,再将x=9代入函数解析式求出y的值,可得出球能过球网,再根据y=0求出对应的自变量的值,再与18 比较大小,即可得出答案。
8.答案:B
解析:解:由题意,抛物线的解析式为y=at(t﹣9),把(1,8)代入可得a=﹣1,
∴y=﹣t2+9t=﹣(t﹣4.5)2+20.25,
∴足球距离地面的最大高度为20.25m,故①错误,
∴抛物线的对称轴t=4.5,故②正确,
∵t=9时,y=0,
∴足球被踢出9s时落地,故③正确,
∵t=1.5时,y=11.25,故④错误.
∴正确的有②③,
故答案为:B.
分析:根据题意,抛物线的解析式为y=at(t﹣9),把(1,8)代入求出a的值,得出函数解析式,再将函数解析式化成顶点式,即可对各选项一一判断即可。
9.答案:A
解析:设矩形ABCD的边AB为x米,则宽为40-2x,
S=(40-2x)x= -2x2+40x.
要使矩形ABCD面积最大,
则
即x的长为10m.
故选A.
分析:求二次函数的最大(小)值有三种方法,第一种可由图象直接得出,第二种是配方法,第三种是公式法,常用的是后两种方法,当二次系数a的绝对值是较小的整数时,用配方法较好,如y= -x2-2x+5,y=3x2-6x+1等用配方法求解比较简单.
10.答案:D
解析:解:y=x2﹣8x+15的图象与x轴交点(3,0)和(5,0),
|MN|=2,
设p点(x,y),
y=x2﹣8x+15,
面积==|MN| |y|,
可得y1=,或者y2=﹣
当y=时,x=;
当y=﹣时,x=
所以共有四个点.
故选D.
分析:由题可求出MN的长,即△MNP的底边已知,要求面积为,那么根据面积即可求出高,只要把相应的y值代入即可解答.
11.答案:B
解析:由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断。
解:由抛物线的开口向下知a<0
对称轴为,
∴a、b异号,即b>0.
与y轴的交点坐标为(0,2.4),
∴c=2.4.
把点(12,0)代入解析式得,144a+12b+2.4=0
∴144a=-2.4-12b,12b=-2.4-144a,
∴144a+12b=-2.12b+2.4<144a,
∴144a<-2.4,12b<-144a
∴a<,b<-12a
∴①④正确,②错误,
∵此题是实际问题,
∴x≥0,
∴③a-b+c>0错误.
故选B.
点评:解决此类题目要熟练掌握二次函数的图象和性质,解题的关键是注意数形结合思想的应用。
12.答案:B
解析:根据图(2)可以判断三角形的面积变化分为三段,可以判断出当点P到达点E时点Q到达点C,从而得到BC、BE的长度,再根据M、N是从5秒到7秒,可得ED的长度,然后表示出AE的长度,根据勾股定理求出AB的长度,然后针对各小题分析解答即可.
解:根据图(2)可得,当点P到达点E时点Q到达点C,
∵点P、Q的运动的速度都是1cm/秒,
∴BC=BE=5,
∴AD=BE=5,故A正确;
又∵从M到N的变化是2,
∴ED=2,
∴AE=AD-ED=5-2=3,
在Rt△ABE中,
∴cos∠ABE==,故B错误;
如图(1)过点P作PF⊥BC于点F,
∵AD∥BC,
∴∠AEB=∠PBF,
∴sin∠PBF=sin∠AEB==
∴PF=PBsin∠PBF=t,
∴当0<t≤5时,y=BQ PF=t t=t2,故C正确;
当t=秒时,点P在CD上,此时,PD=-BE-ED=-5-2=,
PQ=CD-PD=4-=,
∵=,=,
∴=,
又∵∠A=∠Q=90°,
∴△ABE∽△QBP,故D正确.
由于该题选择错误的,故选:B.
点评:本题考查了动点问题的函数图象,根据图(2)判断出点P到达点E时点Q到达点C是解题的关键,也是本题的突破口
13.答案:11
解析:解:根据题意可知 ,
则 ,
解得 , ,
∵ ,
∴ ,
故铅球推出的距离是11米.
故答案为:11.
分析:根据铅球落地时,高度y=0,把实际问题可理解为当y=0时,求x的值即可.
14.答案:100(1+x)2
解析:解:∵一月份新产品的研发资金为100元,
2月份起,每月新产品的研发资金与上月相比增长率都是x,
∴2月份研发资金为100(1+x),
∴三月份的研发资金为y=100(1+x)×(1+x)=100(1+x)2.
故答案为:100(1+x)2.
分析:根据三月份的研发资金为y=一月份的研发资金×(1+增长率)2,就可得出结果。
15.答案:l=﹣2m2+8m+12
解析:解: 把x=m代入抛物线y=﹣x 2+6x中,得AD=﹣m 2+6m
把y=﹣m2+6m代入抛物线y=﹣x2+6x中,得
﹣m2+6m=﹣x2+6x
解得x1=m,x2=6﹣m
∴C的横坐标是6﹣m,故AB=6﹣m﹣m=6﹣2m
∴矩形的周长是l=2(﹣m2+6m)+2(6﹣2m)
即l=﹣2m2+8m+12.
分析:因为矩形的周长l=2(AB+AD),要求周长,只需求得AB和AD的长即可。由矩形的性质和已知条件可知,点A、D的横坐标相同,点C、D的纵坐标相同,所以只需把x=m代入解析式可得点D的纵坐标,把点D的纵坐标代入解析式可求得点C的横坐标,于是线段AB和AD的长可求解,则 l与m的函数解析式 可求解。
16.答案:3
解析:解:如图,
∵抛物线y=x2﹣k的顶点为P,
∴P点的坐标为:(0,﹣k),
∴PO=k,
∵抛物线y=x2﹣k与x轴交于A、B两点,且△ABP是正三角形,
∴OA=OB,∠OPB=30°,
∴tan30°= = ,
∴OB= k,
∴点B的坐标为:( k,0),点B在抛物线y=x2﹣k上,
∴将B点代入y=x2﹣k,得:
0=( k)2﹣k,
整理得: ﹣k=0,
解得:k1=0(不合题意舍去),k2=3.
故答案为:3.
分析:先求出抛物线的顶点P的坐标,得出OP的长,再由 △ABP是正三角形,利用解直角三角形求出OB的值,就可得出点B的坐标,然后将点B的坐标代入函数解析式,就可求出k的值。
17.答案:(60+x)
解析:解:由函数的图象可知点(30,2700)和点(60,0)满足解析式w=mx2+n,
∴ ,
解得: ,
∴w=﹣x2+3600,
设销售量为a,则a(60﹣x)=w,
即a(60﹣x)=﹣x2+3600,
解得:a=60+x ,
故答案为:60+x.
分析:由函数的图象可知点(30,2700)和点(60,0)满足解析式w=mx2+n,可求出w与x的关系式,设销售量为a,则每件工艺品的利润 为(60﹣x)元,根据总利润=每件工艺品的利润×销售量,列式整理即可求出。
18.答案:解:由题意得:y=x× =﹣ x2+20x,自变量x的取值范围是0<x≤25.
解析:由长方形的性质可将AB表示成AB=
,则长方形的面积=长
× 宽=AB
× BC;易得
自变量x的取值范围是0<x≤25.
19.答案:解:根据题意可得:
y=x[200+6(80﹣x)]
=﹣6x2+680x.
解析: 该公园每天的门票收入y=门票的单价×每天进园的人数,列出函数解析式即可。
20.答案:解:∵用总长为L米的篱笆围成长方形场地,一边长度x米,
∴另一边长为:( ﹣x)m,
故x( ﹣x)=60,
则L= +2x,(0<x< ).
解析:根据长方形的周长表示出长方形的另一边,再利用长方形的面积=长×宽,就可得出L与x的函数解析式,然后求出x的取值范围。
21.答案:(1)设正方形画板的边长为xdm,出售价为每张y元,且y=kx+b(k≠0) (1分)
由表格中的数据可得,,解得
从而一张画板的出售价y与边长x之间满足函数关系式y=6x+100
(2)设每张画板的成本价为ax2,利润W=6x+100-ax2
当x=30时,W=130,180+100-900a=130,得a=
一张画板的利润W与边长x之间满足函数关系式W=-x2+6x+100
由W=-16(x-18)2+154,知当x=18时,W有最大值,W最大=154
因此当正方形画板的边长为18dm时,可获最大利润154元.
解析:(1)每张画板的成本价与它的面积成正比例,可设其解析式为y成本价=ax2,每张画板的出售价由基础价和浮动价两部分组成,其中基础价与画板的大小无关,是固定不变的.浮动价与画板的边长成正比例.可设y出售价=kx+b.把表中数据代入即可求出结论;
(2)由y利润=y出售价-y成本价,可得出二次函数,求出其最大值即可.
22.答案:解:(1)将B、C点代入函数解析式,得
,
解得,
这个二次函数y=x2+bx+c的解析式为y=x2﹣2x﹣3;
(2)四边形POP′C为菱形,得
OC与PP′互相垂直平分,得
yP=,即x2﹣2x﹣3=﹣,
解得x1=,x2=(舍),P(,﹣);
(3)∠PBC<90°,
①如图1
当∠PCB=90°时,过P作PH⊥y轴于点H,
BC的解析式为y=x﹣3,CP的解析式为y=﹣x﹣3,
设点P的坐标为(m,﹣3﹣m),
将点P代入代入y═x2﹣2x﹣3中,
解得m1=0(舍),m2=1,即P(1,﹣4);
AO=1,OC=3,CB==3,CP==,
此时=3,△AOC∽△PCB;
②如图2
,
当∠BPC=90°时,作PH⊥y轴于H,作BD⊥PH于D,
BC的解析式为y=x﹣3,CP的解析式为y=x﹣3,
设点P的坐标为(m,m2﹣2m﹣3),
由Kcp Kpb=﹣1,得m=或(舍去)
此时,==≠=3,
以P、C、B为顶点的三角形与△AOC不相似;
综上所述:P、C、B为顶点的三角形与△AOC相似,此时点P的坐标(1,﹣4).
解析:(1)根据待定系数法,可得函数解析式;
(2)根据菱形的对角线互相垂直平分,可得P点的纵坐标,根据自变量与函数值的对应关系,可得答案;
(3)分类讨论:①当∠PCB=90°,根据互相垂直的两条直线的一次项系数互为负倒数,可得BP的解析式,根据自变量与函数值的对应关系,可得P点坐标;根据勾股定理,可得BC,CP的长,根据两组对边对应成比例且夹角相等的两个三角形相似,可得答案;
②当∠BPC=90°时,根据相似三角形的性质,可得P点的坐标,根据两组对边对应成比例且夹角相等的两个三角形相似,可得答案.
将来的某一天,你会感谢曾经努力的自己!
