【2024春人教版八下数学高效实用课件】16.1.2 二次根式的性质 课件(共25张PPT)
文档属性
| 名称 | 【2024春人教版八下数学高效实用课件】16.1.2 二次根式的性质 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-19 00:00:00 | ||
图片预览






文档简介
(共25张PPT)
人教八下数学
同步优质课件
人教版八年级下册
16.1.2
二次根式的性质
第十六章 二次根式
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
1.探索二次根式的性质.
2.运用二次根式的性质进行化简计算.
学习目标
难点
难点
解:正方形的边长为 ,
用边长表示正方形的面积为 ,
又∵面积为a,
即 .
如图是一块正方形地毯,面积为a,求它的边长,并用所求得的边长表示出面积,你发现了什么?
这个式子是不是对所有的二次根式都成立呢?
新课引入
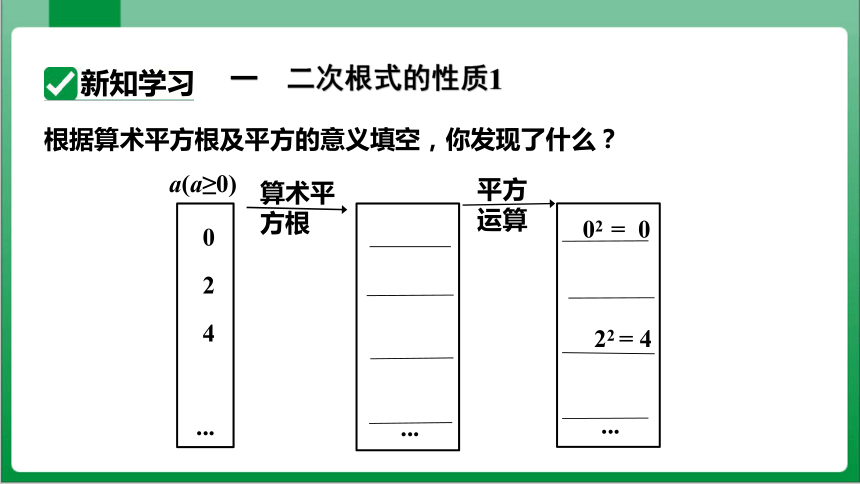
一 二次根式的性质1
根据算术平方根及平方的意义填空,你发现了什么?
...
算术平方根
平方运算
0
2
4
...
a(a≥0)
02 = 0
...
22 = 4
新知学习
...
算术平方根
平方运算
0
2
4
...
a(a≥0)
02 = 0
...
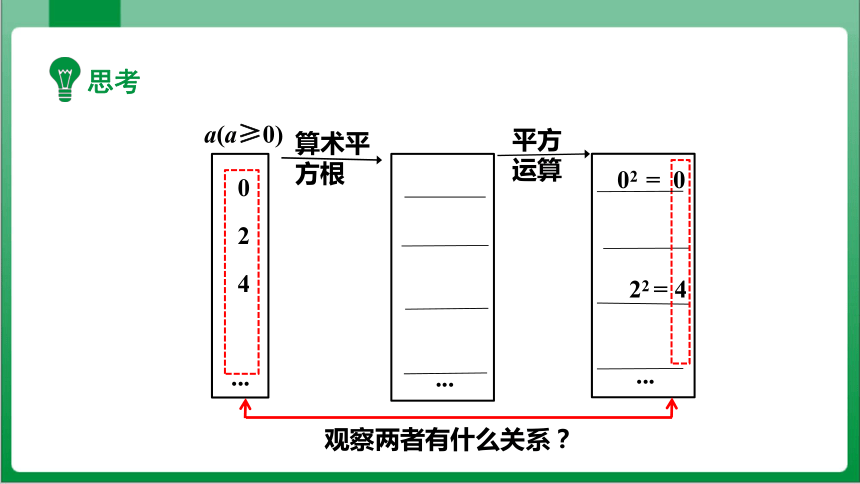
观察两者有什么关系?
22 = 4
思考
你发现了什么?
是2的算术平方根,根据算术平方根的意义,
是一个平方等于2的非负数.因此有 .
同理, 分别是0,4, 的算术平方根,因此有
.
归纳
二次根式的性质1:
一般地, =a (a≥0).
即一个非负数的算术平方根的平方等于它本身.
例1 计算:
解:
(2)用到幂的哪条基本性质呢?
积的乘方:(ab)2=a2b2
二 二次根式的性质2
...
平方运算
算术平方根
2
0.1
0
...
a(a≥0)
2
...
填空:
...
平方运算
算术平方根
2
0.1
0
...
a(a≥0)
2
...
观察两者有什么关系?
=a (a≥0).
思考
...
平方运算
算术平方根
-2
-0.1
...
2
...
观察两者有什么关系?
a(a<0)
当a<0时, =
?
-a
=-a (a<0).
即任意一个数的平方的算术平方根等于它本身的绝对值.
归纳
a (a≥0)
-a (a<0)
二次根式的性质2:
例2 化简:
解:
思考
如何区别 与 ?
从运算顺序看
从取值范围看
从运算结果看
先开方,后平方
先平方,后开方
a≥0
a取任何实数
a
|a|
意义
表示一个非负数a的算术平方根的平方
表示一个实数a的平方的算术平方根
三 代数式的定义
用基本运算符号(基本运算包括加、减、乘、除、乘方和开方)把数或表示数的字母连接起来的式子,我们称这样的式子为代数式.
初中阶段所学的代数式主要有哪几类?
代数式
整式
分式
二次根式
例3 下列式子是代数式的有 ( )
①a2+b2 ; ② ; ③13; ④x=2;
⑤3×(4 -5);⑥x-1≤0; ⑦10x+5y=15 ; ⑧
A.3个 B.4个 C.5个 D.6个
C
解析:代数式中的运算符号包括加、减、乘、除、乘方和开方.
④⑥⑦中有等号和不等号,所以不是代数式.
1.计算:
解:
随堂练习
(3)
而3.14<π,要注意a的正负性.
2.化简:
解:
3.实数a、b在数轴上的对应点如图所示,化简:
解:由数轴可知a<0,b>0,a-b<0,
∴原式=|a|-|b|+|a-b|
=-a-b-(a-b)
=-2a.
a
b
利用数轴和二次根式的性质进行化简,关键是要根据a,b的大小讨论绝对值内式子的符号.
4.一条河的水流速度是2.5 km/h,船在静水中的速度是 v km/h,用代数式表示船在这条河中顺水行驶和逆水行驶时的速度;
解:船在这条河中顺水行驶的速度是 km/h,逆水行驶的速度是 km/h.
性质1
二次根式
的性质
性质2
|a|=
课堂小结
a (a≥0)
-a (a<0)
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
人教八下数学
同步优质课件
人教版八年级下册
16.1.2
二次根式的性质
第十六章 二次根式
学习目标
新课引入
新知学习
课堂小结
1
2
3
4
1.探索二次根式的性质.
2.运用二次根式的性质进行化简计算.
学习目标
难点
难点
解:正方形的边长为 ,
用边长表示正方形的面积为 ,
又∵面积为a,
即 .
如图是一块正方形地毯,面积为a,求它的边长,并用所求得的边长表示出面积,你发现了什么?
这个式子是不是对所有的二次根式都成立呢?
新课引入
一 二次根式的性质1
根据算术平方根及平方的意义填空,你发现了什么?
...
算术平方根
平方运算
0
2
4
...
a(a≥0)
02 = 0
...
22 = 4
新知学习
...
算术平方根
平方运算
0
2
4
...
a(a≥0)
02 = 0
...
观察两者有什么关系?
22 = 4
思考
你发现了什么?
是2的算术平方根,根据算术平方根的意义,
是一个平方等于2的非负数.因此有 .
同理, 分别是0,4, 的算术平方根,因此有
.
归纳
二次根式的性质1:
一般地, =a (a≥0).
即一个非负数的算术平方根的平方等于它本身.
例1 计算:
解:
(2)用到幂的哪条基本性质呢?
积的乘方:(ab)2=a2b2
二 二次根式的性质2
...
平方运算
算术平方根
2
0.1
0
...
a(a≥0)
2
...
填空:
...
平方运算
算术平方根
2
0.1
0
...
a(a≥0)
2
...
观察两者有什么关系?
=a (a≥0).
思考
...
平方运算
算术平方根
-2
-0.1
...
2
...
观察两者有什么关系?
a(a<0)
当a<0时, =
?
-a
=-a (a<0).
即任意一个数的平方的算术平方根等于它本身的绝对值.
归纳
a (a≥0)
-a (a<0)
二次根式的性质2:
例2 化简:
解:
思考
如何区别 与 ?
从运算顺序看
从取值范围看
从运算结果看
先开方,后平方
先平方,后开方
a≥0
a取任何实数
a
|a|
意义
表示一个非负数a的算术平方根的平方
表示一个实数a的平方的算术平方根
三 代数式的定义
用基本运算符号(基本运算包括加、减、乘、除、乘方和开方)把数或表示数的字母连接起来的式子,我们称这样的式子为代数式.
初中阶段所学的代数式主要有哪几类?
代数式
整式
分式
二次根式
例3 下列式子是代数式的有 ( )
①a2+b2 ; ② ; ③13; ④x=2;
⑤3×(4 -5);⑥x-1≤0; ⑦10x+5y=15 ; ⑧
A.3个 B.4个 C.5个 D.6个
C
解析:代数式中的运算符号包括加、减、乘、除、乘方和开方.
④⑥⑦中有等号和不等号,所以不是代数式.
1.计算:
解:
随堂练习
(3)
而3.14<π,要注意a的正负性.
2.化简:
解:
3.实数a、b在数轴上的对应点如图所示,化简:
解:由数轴可知a<0,b>0,a-b<0,
∴原式=|a|-|b|+|a-b|
=-a-b-(a-b)
=-2a.
a
b
利用数轴和二次根式的性质进行化简,关键是要根据a,b的大小讨论绝对值内式子的符号.
4.一条河的水流速度是2.5 km/h,船在静水中的速度是 v km/h,用代数式表示船在这条河中顺水行驶和逆水行驶时的速度;
解:船在这条河中顺水行驶的速度是 km/h,逆水行驶的速度是 km/h.
性质1
二次根式
的性质
性质2
|a|=
课堂小结
a (a≥0)
-a (a<0)
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
