第九章 多边形复习课课件(共27张PPT) 华东师大版七年级数学下册
文档属性
| 名称 | 第九章 多边形复习课课件(共27张PPT) 华东师大版七年级数学下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 179.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-19 17:57:14 | ||
图片预览






文档简介
(共27张PPT)
第九章 多边形
复习课
学习导航
学习目标
知识梳理
考点探究
当堂检测
课堂总结
一、学习目标
1.知道三角形的中线、角平分线和高,并能画出这三种线段;
2.能运用三角形的三边关系判断三角形组成;
3.知道三角形的内角和、外角性质、外角和以及多边形的内角和、外角和,并应用它们解决实际问题;
4.举例说明某些正多边形能够铺满地面的道理.
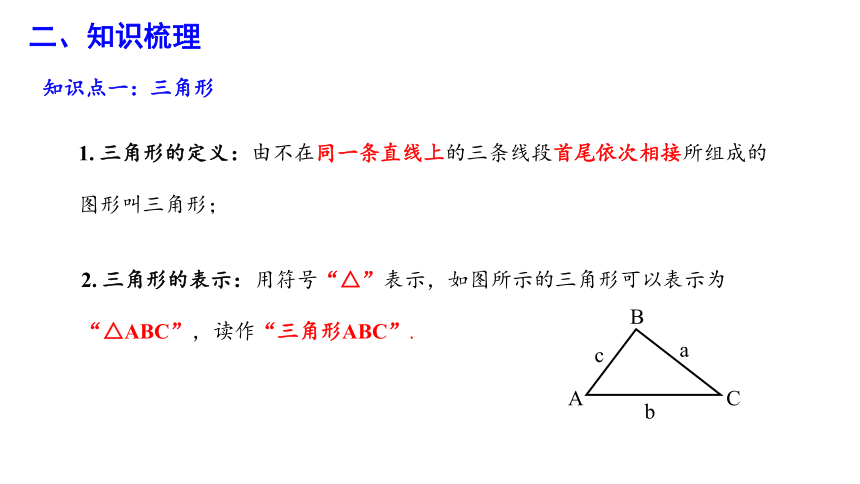
1. 三角形的定义:由不在同一条直线上的三条线段首尾依次相接所组成的图形叫三角形;
知识点一:三角形
A
B
C
a
b
c
2. 三角形的表示:用符号“△”表示,如图所示的三角形可以表示为“△ABC”,读作“三角形ABC”.
二、知识梳理
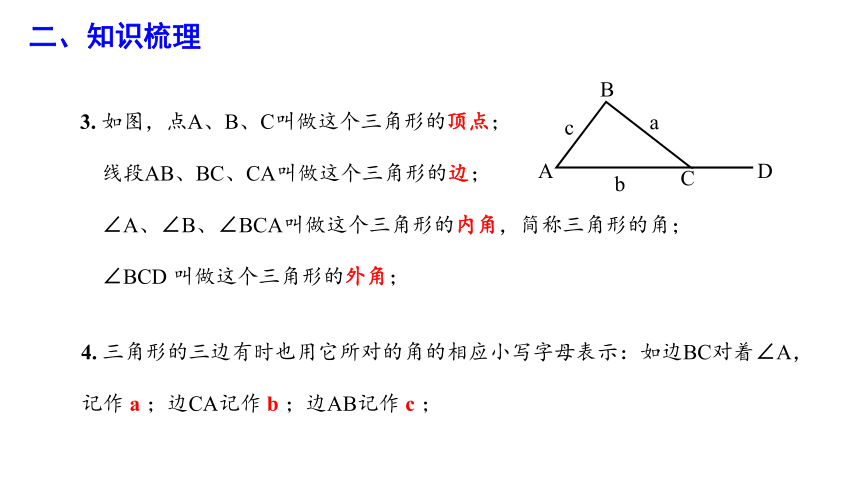
二、知识梳理
3. 如图,点A、B、C叫做这个三角形的顶点;
线段AB、BC、CA叫做这个三角形的边;
∠A、∠B、∠BCA叫做这个三角形的内角,简称三角形的角;
∠BCD 叫做这个三角形的外角;
A
B
C
a
b
c
D
4. 三角形的三边有时也用它所对的角的相应小写字母表示:如边BC对着∠A,记作 a ;边CA记作 b ;边AB记作 c ;
二、知识梳理
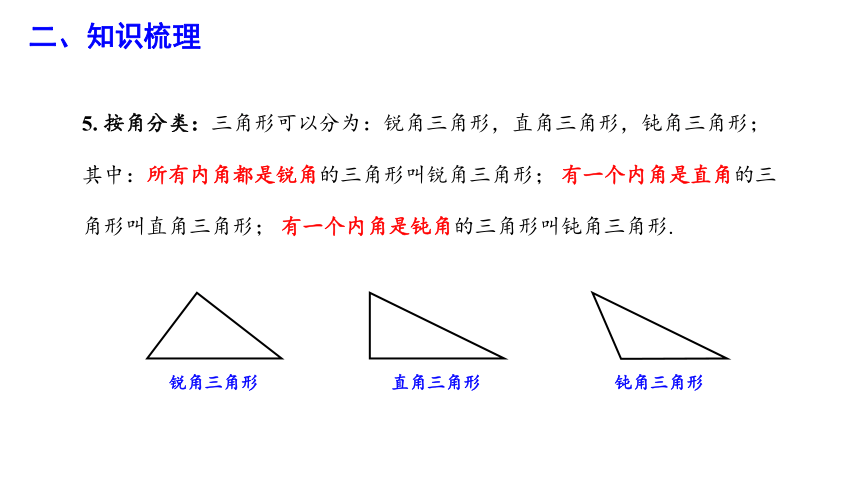
5. 按角分类:三角形可以分为:锐角三角形,直角三角形,钝角三角形;
其中:所有内角都是锐角的三角形叫锐角三角形; 有一个内角是直角的三角形叫直角三角形; 有一个内角是钝角的三角形叫钝角三角形.
锐角三角形
直角三角形
钝角三角形
二、知识梳理
6. 按边分类:三角形可以分为:不等边三角形和等腰三角形;
等腰三角形又可分为:腰和底不相等的等腰三角形和等边三角形;
等腰三角形
等边三角形
三角形
不等边三角形
底和腰不等的等腰三角形
等腰三角形:有两条边相等的三角形;相等的两边叫做等腰三角形的腰;
等边三角形:三条边都相等的三角形;称为等边三角形(或正三角形).
二、知识梳理
7. 三角形的三线:
中线:三角形的一个顶点与它的对边的中点的连线叫做三角形的中线;
角平分线:三角形的一个内角的平分线与这个角的对边的交点至顶点的线段;
高:过三角形的顶点作对边(或对边的延长线)的垂线 ,顶点与垂足间的线段叫做三角形的高.
二、知识梳理
8. 三角形的内角和和外角和:
内角和:三角形的内角和等于 180°;
推论 1:直角三角形两锐角 互余 ;
外角的性质:性质 1:三角形的一个外角等于 与它不相邻的两内角的和;
性质 2:三角形的一个外角大于 任何一个与它不相邻的内角;
外角和:三角形的外角和等于 360°.
二、知识梳理
9. 三角形的三边关系:
结论 1 :任意两边之和 大于 第三边;
结论 2 :任意两边之差 小于 第三边;
三角形第三边的取值范围是:两边之差 < 第三边 < 两边之和;
应用:三角形的稳定性.
二、知识梳理
知识点二:多边形
1. 多边形的定义:由 n 条不在同一直线上的线段首尾顺次连结组成的平面图形,称为 n 边形.
2. 正多边形:如果多边形的各边都相等,各角也都相等,那么就称它为正多边形.
二、知识梳理
3. 多边形的对角线公式:
一个顶点对角线条数:从 n 边形的一个顶点出发可以画 ( n – 3 ) 条对角线;
多边形所有对角线条数:n 边形的所有顶点一共可以画 条对角线;
4. 多边形的内角和定理:n 边形的内角和为 ( n – 2 )·180°;
5. 多边形的外角和定理:任意多边形的外角和都为 360°.
二、知识梳理
6. 多边形能铺满地面的条件是:拼接在同一个顶点处的各个多边形的内角之和等于360°.
例如:
正三角形
正六边形
例1:下列说法错误的是( )
A. 三角形的三条中线都在三角形内,且平分三角形的面积
B. 直角三角形的高线只有一条
C. 三角形的三条角平分线都在三角形内
D. 钝角三角形内只有一条高线
三、考点探究
考点一 三角形的角平分线、中线和高
分析:根据三角形的角平分线、中线和高的概念逐一进行判断.
B
三、考点探究
方法总结 1:
(1)三角形的三条角平分线、三条中线、三条高(或延长线)分别相交于一点;
(2)其中中线平分三角形面积,直角三角形有两条高线在边上,钝角三角形有两条高线在三角形外面.
〖当堂检测〗
1. 如图所示,AD 是 △ABC 的中线,已知 △ABD 比 △ACD 的周长大 6cm,则 AB 与 AC 的差为( )
A. 12 cm B. 6 cm C. 3 cm D. 2 cm
B
三、考点探究
考点二 三角形的三边关系
例2:已知两条线段的长分别是 3cm、8cm ,要想拼成一个三角形,且第三条线段 a 的长为奇数,问第三条线段应取多长?
解:由三角形两边之和大于第三边,两边之差小于第三边,得:
8 – 3 < a < 8 + 3;
解得:5 < a < 11;
又第三边长 a 为奇数;
分析:根据三角形的三边关系满足 8 – 3 < a < 8 + 3 解答即可.
故第三条边长为 7 cm 或 9 cm.
三、考点探究
方法总结 2:
(1)三角形两边之和大于第三边;可以用来判断三条线段能否组成三角形,在运用中一定要注意检查是否任意两边的和都大于第三边,也可以直接检查较小两边之和是否大于第三边;
(2)三角形的三边关系在求线段的取值范围以及在证明线段的不等关系中有着重要的作用.
〖当堂检测〗
2. 已知四组线段的长分别如下,以各组线段为边,能组成三角形的是 ( )
A.1,2,3 B.2,5,8
C.3,4,5 D.4,5,10
C
3. 以线段 3、4、x – 5 为边组成三角形,那么 x 的取值范围是 .
6 < x < 12
三、考点探究
考点三 三角形内角和与外角和
例3:下列条件中,能判定 △ABC 为直角三角形的是( )
A. ∠A = 2∠B = 3∠C B. ∠A + ∠B = ∠C
C. ∠A = ∠B = 30° D. ∠A = ∠B = ∠C
分析:根据“三角形内角和定理和为180°”求出各选项中△ABC的内角,然后根据直角三角形的判定方法进行判断.
B
三、考点探究
方法总结 3:
(1) 三角形内角和定理:三角形内角和是180°.
(2)推论 1:直角三角形两锐角互补;
推论 2:有两个角的和为90°的三角形是直角三角形.
(3)已知三角形中的三个角之间关系,可运用方程思想来求各角的度数.
三、互动探究
分析:利用直角三角形两锐角互余可求出 ∠ABE 的度数;
再根据外角的性质 1 ,即可求出 ∠BPC 的度数.
解:已知 ∠A = 50°,BE ⊥ AC;
例 4:如图,在锐角三角形 ABC 中,CD、BE 分别是 AB、AC 边上的高,且 CD、BE 交于一点 P ,若 ∠A = 50°,求 ∠BPC 的度数.
因为 ∠BPC是△DBP的一个外角;
所以:∠ABE = 90°– 50°= 40°;
B
C
A
E
D
P
又CD ⊥ AB,且 ∠ABE = ∠DBP = 40°;
所以 ∠BPC = ∠DBP + ∠BDP = 40°+ 90°= 130°.
〖当堂检测〗
4. 在一个直角三角形中,有一个锐角等于60°,则另一个锐角的度数为_____.
30°
5. 若一个三角形的三个外角之比为 2 ∶ 3 ∶ 4 ,则与之对应的三个内角度数之比为 ( )
A. 4 ∶ 3 ∶ 2 B. 3 ∶ 2 ∶ 4 C. 5 ∶ 3 ∶ 1 D. 4 ∶ 2 ∶ 3
C
三、考点探究
考点四 多边形的内角和与外角和
例 5:已知一个正多边形的每个内角都是其相邻外角度数的4倍,求这个正多边形的边数.
解:设此多边形的外角的度数为 x,则内角的度数为 4x;
解得:x = 36°;
因为多边形的外角和为360°;
所以边数 n = 360°÷ 36°= 10 边;
故这个正多边形为 10 边形.
则 x + 4x = 180°;
分析:根据题意列出内外角关系式,算出外角的度数,再算出边数即可;
三、考点探究
方法总结 4:
(1)在多边形的有关求边数或内角、外角度数的问题中,要注意内角与外角之间的转化,以及定理的运用;
(2)在求边数的问题中,常常利用定理列出方程,再求得边数.
〖当堂检测〗
6. 一个正多边形的每一个内角都等于120 °,则其边数是 .
6
四、课堂总结
三角形
三角形的高线
三角形的中线:将三角形面积二等分
三角形的角平分线
有关线段
多边形
n 边形的内角和为 (n – 2)·180°
多边形的外角和为 360°
平面镶嵌
三边关系
三角形任意两边之和大于第三边
三角形的稳定性
有关的角
三角形的内角和为 180°
三角形的外角和为 360°
第九章 多边形
复习课
学习导航
学习目标
知识梳理
考点探究
当堂检测
课堂总结
一、学习目标
1.知道三角形的中线、角平分线和高,并能画出这三种线段;
2.能运用三角形的三边关系判断三角形组成;
3.知道三角形的内角和、外角性质、外角和以及多边形的内角和、外角和,并应用它们解决实际问题;
4.举例说明某些正多边形能够铺满地面的道理.
1. 三角形的定义:由不在同一条直线上的三条线段首尾依次相接所组成的图形叫三角形;
知识点一:三角形
A
B
C
a
b
c
2. 三角形的表示:用符号“△”表示,如图所示的三角形可以表示为“△ABC”,读作“三角形ABC”.
二、知识梳理
二、知识梳理
3. 如图,点A、B、C叫做这个三角形的顶点;
线段AB、BC、CA叫做这个三角形的边;
∠A、∠B、∠BCA叫做这个三角形的内角,简称三角形的角;
∠BCD 叫做这个三角形的外角;
A
B
C
a
b
c
D
4. 三角形的三边有时也用它所对的角的相应小写字母表示:如边BC对着∠A,记作 a ;边CA记作 b ;边AB记作 c ;
二、知识梳理
5. 按角分类:三角形可以分为:锐角三角形,直角三角形,钝角三角形;
其中:所有内角都是锐角的三角形叫锐角三角形; 有一个内角是直角的三角形叫直角三角形; 有一个内角是钝角的三角形叫钝角三角形.
锐角三角形
直角三角形
钝角三角形
二、知识梳理
6. 按边分类:三角形可以分为:不等边三角形和等腰三角形;
等腰三角形又可分为:腰和底不相等的等腰三角形和等边三角形;
等腰三角形
等边三角形
三角形
不等边三角形
底和腰不等的等腰三角形
等腰三角形:有两条边相等的三角形;相等的两边叫做等腰三角形的腰;
等边三角形:三条边都相等的三角形;称为等边三角形(或正三角形).
二、知识梳理
7. 三角形的三线:
中线:三角形的一个顶点与它的对边的中点的连线叫做三角形的中线;
角平分线:三角形的一个内角的平分线与这个角的对边的交点至顶点的线段;
高:过三角形的顶点作对边(或对边的延长线)的垂线 ,顶点与垂足间的线段叫做三角形的高.
二、知识梳理
8. 三角形的内角和和外角和:
内角和:三角形的内角和等于 180°;
推论 1:直角三角形两锐角 互余 ;
外角的性质:性质 1:三角形的一个外角等于 与它不相邻的两内角的和;
性质 2:三角形的一个外角大于 任何一个与它不相邻的内角;
外角和:三角形的外角和等于 360°.
二、知识梳理
9. 三角形的三边关系:
结论 1 :任意两边之和 大于 第三边;
结论 2 :任意两边之差 小于 第三边;
三角形第三边的取值范围是:两边之差 < 第三边 < 两边之和;
应用:三角形的稳定性.
二、知识梳理
知识点二:多边形
1. 多边形的定义:由 n 条不在同一直线上的线段首尾顺次连结组成的平面图形,称为 n 边形.
2. 正多边形:如果多边形的各边都相等,各角也都相等,那么就称它为正多边形.
二、知识梳理
3. 多边形的对角线公式:
一个顶点对角线条数:从 n 边形的一个顶点出发可以画 ( n – 3 ) 条对角线;
多边形所有对角线条数:n 边形的所有顶点一共可以画 条对角线;
4. 多边形的内角和定理:n 边形的内角和为 ( n – 2 )·180°;
5. 多边形的外角和定理:任意多边形的外角和都为 360°.
二、知识梳理
6. 多边形能铺满地面的条件是:拼接在同一个顶点处的各个多边形的内角之和等于360°.
例如:
正三角形
正六边形
例1:下列说法错误的是( )
A. 三角形的三条中线都在三角形内,且平分三角形的面积
B. 直角三角形的高线只有一条
C. 三角形的三条角平分线都在三角形内
D. 钝角三角形内只有一条高线
三、考点探究
考点一 三角形的角平分线、中线和高
分析:根据三角形的角平分线、中线和高的概念逐一进行判断.
B
三、考点探究
方法总结 1:
(1)三角形的三条角平分线、三条中线、三条高(或延长线)分别相交于一点;
(2)其中中线平分三角形面积,直角三角形有两条高线在边上,钝角三角形有两条高线在三角形外面.
〖当堂检测〗
1. 如图所示,AD 是 △ABC 的中线,已知 △ABD 比 △ACD 的周长大 6cm,则 AB 与 AC 的差为( )
A. 12 cm B. 6 cm C. 3 cm D. 2 cm
B
三、考点探究
考点二 三角形的三边关系
例2:已知两条线段的长分别是 3cm、8cm ,要想拼成一个三角形,且第三条线段 a 的长为奇数,问第三条线段应取多长?
解:由三角形两边之和大于第三边,两边之差小于第三边,得:
8 – 3 < a < 8 + 3;
解得:5 < a < 11;
又第三边长 a 为奇数;
分析:根据三角形的三边关系满足 8 – 3 < a < 8 + 3 解答即可.
故第三条边长为 7 cm 或 9 cm.
三、考点探究
方法总结 2:
(1)三角形两边之和大于第三边;可以用来判断三条线段能否组成三角形,在运用中一定要注意检查是否任意两边的和都大于第三边,也可以直接检查较小两边之和是否大于第三边;
(2)三角形的三边关系在求线段的取值范围以及在证明线段的不等关系中有着重要的作用.
〖当堂检测〗
2. 已知四组线段的长分别如下,以各组线段为边,能组成三角形的是 ( )
A.1,2,3 B.2,5,8
C.3,4,5 D.4,5,10
C
3. 以线段 3、4、x – 5 为边组成三角形,那么 x 的取值范围是 .
6 < x < 12
三、考点探究
考点三 三角形内角和与外角和
例3:下列条件中,能判定 △ABC 为直角三角形的是( )
A. ∠A = 2∠B = 3∠C B. ∠A + ∠B = ∠C
C. ∠A = ∠B = 30° D. ∠A = ∠B = ∠C
分析:根据“三角形内角和定理和为180°”求出各选项中△ABC的内角,然后根据直角三角形的判定方法进行判断.
B
三、考点探究
方法总结 3:
(1) 三角形内角和定理:三角形内角和是180°.
(2)推论 1:直角三角形两锐角互补;
推论 2:有两个角的和为90°的三角形是直角三角形.
(3)已知三角形中的三个角之间关系,可运用方程思想来求各角的度数.
三、互动探究
分析:利用直角三角形两锐角互余可求出 ∠ABE 的度数;
再根据外角的性质 1 ,即可求出 ∠BPC 的度数.
解:已知 ∠A = 50°,BE ⊥ AC;
例 4:如图,在锐角三角形 ABC 中,CD、BE 分别是 AB、AC 边上的高,且 CD、BE 交于一点 P ,若 ∠A = 50°,求 ∠BPC 的度数.
因为 ∠BPC是△DBP的一个外角;
所以:∠ABE = 90°– 50°= 40°;
B
C
A
E
D
P
又CD ⊥ AB,且 ∠ABE = ∠DBP = 40°;
所以 ∠BPC = ∠DBP + ∠BDP = 40°+ 90°= 130°.
〖当堂检测〗
4. 在一个直角三角形中,有一个锐角等于60°,则另一个锐角的度数为_____.
30°
5. 若一个三角形的三个外角之比为 2 ∶ 3 ∶ 4 ,则与之对应的三个内角度数之比为 ( )
A. 4 ∶ 3 ∶ 2 B. 3 ∶ 2 ∶ 4 C. 5 ∶ 3 ∶ 1 D. 4 ∶ 2 ∶ 3
C
三、考点探究
考点四 多边形的内角和与外角和
例 5:已知一个正多边形的每个内角都是其相邻外角度数的4倍,求这个正多边形的边数.
解:设此多边形的外角的度数为 x,则内角的度数为 4x;
解得:x = 36°;
因为多边形的外角和为360°;
所以边数 n = 360°÷ 36°= 10 边;
故这个正多边形为 10 边形.
则 x + 4x = 180°;
分析:根据题意列出内外角关系式,算出外角的度数,再算出边数即可;
三、考点探究
方法总结 4:
(1)在多边形的有关求边数或内角、外角度数的问题中,要注意内角与外角之间的转化,以及定理的运用;
(2)在求边数的问题中,常常利用定理列出方程,再求得边数.
〖当堂检测〗
6. 一个正多边形的每一个内角都等于120 °,则其边数是 .
6
四、课堂总结
三角形
三角形的高线
三角形的中线:将三角形面积二等分
三角形的角平分线
有关线段
多边形
n 边形的内角和为 (n – 2)·180°
多边形的外角和为 360°
平面镶嵌
三边关系
三角形任意两边之和大于第三边
三角形的稳定性
有关的角
三角形的内角和为 180°
三角形的外角和为 360°
