9.1.3 三角形的三边关系 课件(共17张PPT) 华东师大版七年级数学下册
文档属性
| 名称 | 9.1.3 三角形的三边关系 课件(共17张PPT) 华东师大版七年级数学下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 799.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-19 18:05:01 | ||
图片预览





文档简介
(共17张PPT)
第九章 多边形
9.1 三角形
9.1.3 三角形的三边关系
学习导航
学习目标
合作探究
当堂检测
课堂总结
新课导入
一、学习目标
1.了解三角形的稳定性;
2.能证明三角形的任意两边之和大于第三边及其推论;
3.应用三角形的三边关系解决一些简单的问题; (重点)
二、新课导入
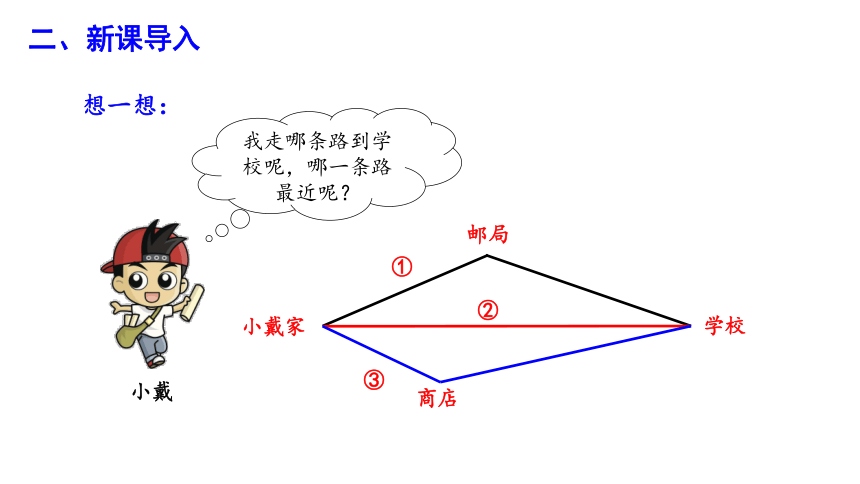
想一想:
小戴
我走哪条路到学校呢,哪一条路最近呢?
学校
小戴家
邮局
①
②
商店
③
情境1:小戴每天去上学有三条路可以选择,请你帮他找出最近的路;
思考:为什么路线②最短,不能选择路线 ① 或 ③ 吗?
三、合作探究
探究一:三角形的三边关系
学校
小戴家
邮局
①
②
商店
③
路线 ② 最近
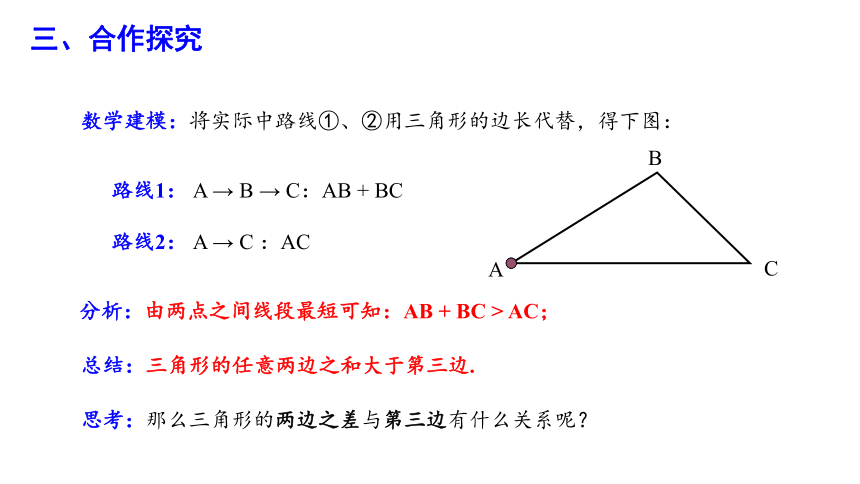
数学建模:将实际中路线①、②用三角形的边长代替,得下图:
三、合作探究
路线1: A → B → C:AB + BC
路线2: A → C :AC
分析:由两点之间线段最短可知:AB + BC > AC;
总结:三角形的任意两边之和大于第三边.
思考:那么三角形的两边之差与第三边有什么关系呢?
A
B
C
证明:如右图,已知 a + b > c ;
推论1:由三角形的任意两边之和大于第三边,可以推出三角形的任意两边之差小于第三边;
根据不等式的性质1得: a + b – b > c – b;
即: a > c – b ;
所以:三角形的两边之差小于第三边;
推论:三角形的任意两边之差小于第三边.
A
B
C
a
c
b
三、合作探究
三角形任意两边的和大于第三边
三角形任意两边的差小于第三边
三角形的三边关系定理总结:
理论依据:两点之间,线段最短.
三、合作探究
练一练:
1. 请判断下列长度的三条线段能组成合适的三角形吗?
(1)3、4、5; (2)6、8、11; (3)3、8、12
分析:根据三角形的三边关系定理,即可解答;
解:(1)3 + 4 > 5,5 – 4 < 3; 所以能组成三角形;
(2)6 + 8 > 11,11 – 8 < 6; 所以能组成三角形;
(3)3 + 8 < 12,12 – 8 > 3; 所以不能组成三角形;
三、合作探究
总结:判断三角形边的取值范围:要同时运用两边之和大于第三边,两边之差小于第三边.
2. 一个三角形的三边长分别为 3,8,x,求 x 的取值范围.
分析:根据三角形的三边关系定理:两边之和大于第三边,两边之差小于第三边,即可解答.
解:∵ 三角形的三边长分别为3,8,x;
∴ 8–3 < x < 8+3,即 5 < x < 11.
三、合作探究
总结:判断三条线段是否可以组成三角形,只需说明:两条较短线段之和大于第三条线段或两条较长线段之差小于第三条线段即可.
3. 现有 2、3、4、5 四种长度的木棒,从中任取三根围成一个三角形,请问可以围成多少种,请详细列举?
分析:根据三角形的三边关系定理,即可解答.
解:① 2、3、4:2 + 3 > 4,4 – 3 < 2;成立;
② 2、3、5:2 + 3 = 5,5 – 3 = 2;不成立;
③ 2、4、5:2 + 4 > 5,5 – 4 < 2;成立;
④ 3、4、5:3 + 4 > 5,5 – 3 < 2;成立;
三、合作探究
活动 1:如图,盖房子时,在木框未安装好之前,木工师傅常常先在木框上斜钉一根木条,为什么要这样做呢?
三、合作探究
探究二:三角形的稳定性
通过日常生活中的实践发现:
四边形受力会改变形状,当钉上木条变为三角形后,形状再也无法改变;这就是说,三角形具有稳定性,四边形没有稳定性.
理解三角形的“稳定性”
定义:只要三角形三条边的三条边固定,那么三角形的形状和大小也就完全确定,三角形的这种性质叫做“三角形的稳定性”;
误区警示:三角形的稳定性不是“拉得动、拉不动”的问题,其实质应是“三角形的三条边确定,其形状和大小就确定了”.
三、合作探究
练一练:
1. 请同学们说出几种三角形的稳定性在生活中的实际应用.
三、合作探究
自行车的车架
桥梁拉杆
四、当堂检测
1. 判断下列长度的三条线段能否拼成三角形?为什么?
(1)3cm、8cm、4cm; (2)5cm、6cm、11cm;(3)5cm、6cm、10cm.
分析:根据三角形的三边关系定理判断即可;
解:(1)不能,因为 3 cm + 4 cm < 8 cm;
(2)不能,因为 5 cm + 6 cm = 11 cm;
(3)能,因为 5 cm + 6 cm > 10 cm.
2. 用一条长为18 cm 的细绳围成一个三角形. 已知该三角形的两边长为 x 和 2x ;若该三角形的边长均为整数,求 x 的值.
解:已知两边长为 x 和 2x ,则第三边长为 (18 – 3x) ;
根据三角形的三边关系列出不等式得:
x + 2x > 18 – 3x , 2x – x < 18 – 3x;
解得 3 < x < 4.5;
因为 x 为整数,故 x = 4 .
四、当堂检测
五、课堂总结
三角形
任意两边之差小于第三边;
任意两边之和大于第三边;
三角形的稳定性
三角形的三边关系
第九章 多边形
9.1 三角形
9.1.3 三角形的三边关系
学习导航
学习目标
合作探究
当堂检测
课堂总结
新课导入
一、学习目标
1.了解三角形的稳定性;
2.能证明三角形的任意两边之和大于第三边及其推论;
3.应用三角形的三边关系解决一些简单的问题; (重点)
二、新课导入
想一想:
小戴
我走哪条路到学校呢,哪一条路最近呢?
学校
小戴家
邮局
①
②
商店
③
情境1:小戴每天去上学有三条路可以选择,请你帮他找出最近的路;
思考:为什么路线②最短,不能选择路线 ① 或 ③ 吗?
三、合作探究
探究一:三角形的三边关系
学校
小戴家
邮局
①
②
商店
③
路线 ② 最近
数学建模:将实际中路线①、②用三角形的边长代替,得下图:
三、合作探究
路线1: A → B → C:AB + BC
路线2: A → C :AC
分析:由两点之间线段最短可知:AB + BC > AC;
总结:三角形的任意两边之和大于第三边.
思考:那么三角形的两边之差与第三边有什么关系呢?
A
B
C
证明:如右图,已知 a + b > c ;
推论1:由三角形的任意两边之和大于第三边,可以推出三角形的任意两边之差小于第三边;
根据不等式的性质1得: a + b – b > c – b;
即: a > c – b ;
所以:三角形的两边之差小于第三边;
推论:三角形的任意两边之差小于第三边.
A
B
C
a
c
b
三、合作探究
三角形任意两边的和大于第三边
三角形任意两边的差小于第三边
三角形的三边关系定理总结:
理论依据:两点之间,线段最短.
三、合作探究
练一练:
1. 请判断下列长度的三条线段能组成合适的三角形吗?
(1)3、4、5; (2)6、8、11; (3)3、8、12
分析:根据三角形的三边关系定理,即可解答;
解:(1)3 + 4 > 5,5 – 4 < 3; 所以能组成三角形;
(2)6 + 8 > 11,11 – 8 < 6; 所以能组成三角形;
(3)3 + 8 < 12,12 – 8 > 3; 所以不能组成三角形;
三、合作探究
总结:判断三角形边的取值范围:要同时运用两边之和大于第三边,两边之差小于第三边.
2. 一个三角形的三边长分别为 3,8,x,求 x 的取值范围.
分析:根据三角形的三边关系定理:两边之和大于第三边,两边之差小于第三边,即可解答.
解:∵ 三角形的三边长分别为3,8,x;
∴ 8–3 < x < 8+3,即 5 < x < 11.
三、合作探究
总结:判断三条线段是否可以组成三角形,只需说明:两条较短线段之和大于第三条线段或两条较长线段之差小于第三条线段即可.
3. 现有 2、3、4、5 四种长度的木棒,从中任取三根围成一个三角形,请问可以围成多少种,请详细列举?
分析:根据三角形的三边关系定理,即可解答.
解:① 2、3、4:2 + 3 > 4,4 – 3 < 2;成立;
② 2、3、5:2 + 3 = 5,5 – 3 = 2;不成立;
③ 2、4、5:2 + 4 > 5,5 – 4 < 2;成立;
④ 3、4、5:3 + 4 > 5,5 – 3 < 2;成立;
三、合作探究
活动 1:如图,盖房子时,在木框未安装好之前,木工师傅常常先在木框上斜钉一根木条,为什么要这样做呢?
三、合作探究
探究二:三角形的稳定性
通过日常生活中的实践发现:
四边形受力会改变形状,当钉上木条变为三角形后,形状再也无法改变;这就是说,三角形具有稳定性,四边形没有稳定性.
理解三角形的“稳定性”
定义:只要三角形三条边的三条边固定,那么三角形的形状和大小也就完全确定,三角形的这种性质叫做“三角形的稳定性”;
误区警示:三角形的稳定性不是“拉得动、拉不动”的问题,其实质应是“三角形的三条边确定,其形状和大小就确定了”.
三、合作探究
练一练:
1. 请同学们说出几种三角形的稳定性在生活中的实际应用.
三、合作探究
自行车的车架
桥梁拉杆
四、当堂检测
1. 判断下列长度的三条线段能否拼成三角形?为什么?
(1)3cm、8cm、4cm; (2)5cm、6cm、11cm;(3)5cm、6cm、10cm.
分析:根据三角形的三边关系定理判断即可;
解:(1)不能,因为 3 cm + 4 cm < 8 cm;
(2)不能,因为 5 cm + 6 cm = 11 cm;
(3)能,因为 5 cm + 6 cm > 10 cm.
2. 用一条长为18 cm 的细绳围成一个三角形. 已知该三角形的两边长为 x 和 2x ;若该三角形的边长均为整数,求 x 的值.
解:已知两边长为 x 和 2x ,则第三边长为 (18 – 3x) ;
根据三角形的三边关系列出不等式得:
x + 2x > 18 – 3x , 2x – x < 18 – 3x;
解得 3 < x < 4.5;
因为 x 为整数,故 x = 4 .
四、当堂检测
五、课堂总结
三角形
任意两边之差小于第三边;
任意两边之和大于第三边;
三角形的稳定性
三角形的三边关系
