9.1.2 三角形的内角和与外角和 第2课时课件(共20张PPT) 华东师大版七年级数学下册
文档属性
| 名称 | 9.1.2 三角形的内角和与外角和 第2课时课件(共20张PPT) 华东师大版七年级数学下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 242.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-19 18:05:49 | ||
图片预览






文档简介
(共20张PPT)
第九章 多边形
9.1 三角形
9.1.2 三角形的内角和与外角和 第2课时
学习导航
学习目标
合作探究
当堂检测
课堂总结
新课导入
一、学习目标
1. 知道三角形的外角和等于 360°;
2. 掌握三角形外角的两条性质,能利用三角形的外角性质解决简单问题.(重点)
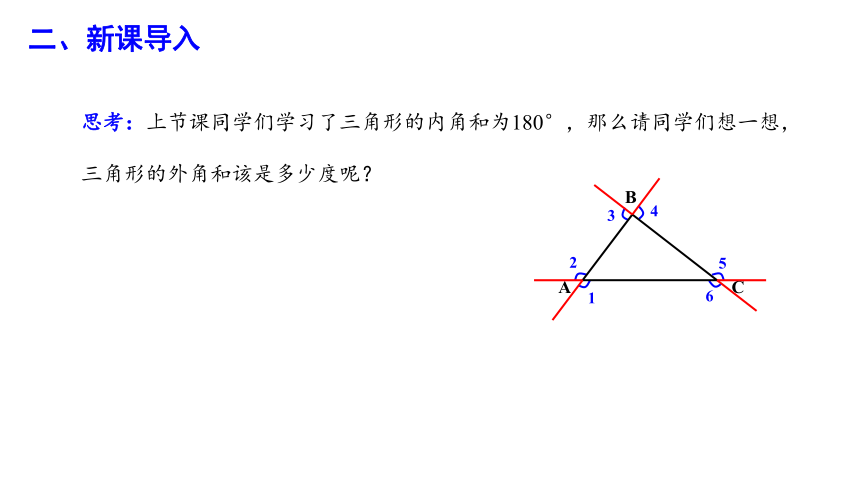
二、新课导入
思考:上节课同学们学习了三角形的内角和为180°,那么请同学们想一想,三角形的外角和该是多少度呢?
1
2
3
4
5
6
B
C
A
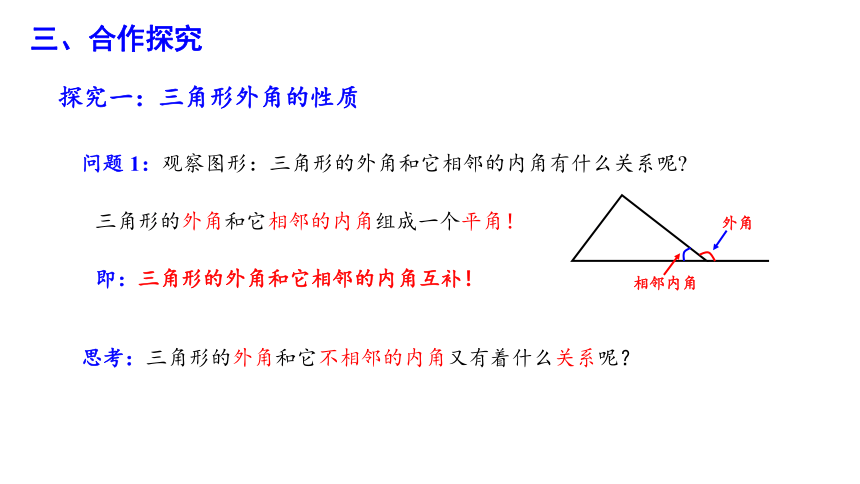
问题 1:观察图形:三角形的外角和它相邻的内角有什么关系呢
外角
相邻内角
三角形的外角和它相邻的内角组成一个平角!
三、合作探究
探究一:三角形外角的性质
即:三角形的外角和它相邻的内角互补!
思考:三角形的外角和它不相邻的内角又有着什么关系呢?
问题2:如图,△ABC的外角∠BCD与∠ A + ∠ B有什么关系?
提出猜想:① ∠ BCD > ∠ A + ∠ B;
② ∠ BCD < ∠ A + ∠ B;
③ ∠ BCD = ∠ A + ∠ B;
某小组提出了如下猜想,请你判断是否正确,并说明理由;
分析:利用三角形内角和定理及平角的性质证明即可;
三、合作探究
证明:猜想 ③ 正确;
在△ ABC 中:∠ A + ∠ B + ∠ ACB = 180°
(三角形内角和定理);
又∠ ACD 是一个平角:即∠ ACB + ∠ DCB = 180°;
故: ∠ A + ∠ B = ∠ DCB (等量代换);
由上可知:猜想 ③ 正确;
结论:三角形的任一外角等于其不相邻的两内角之和.
三、合作探究
问题3:如图,△ABC的外角∠BCD与∠ A、∠ B 分别有什么关系?
提出猜想: ∠BCD > ∠ A;∠BCD > ∠ B;
分析:利用问题2的结论即可证明;
证明:已知:∠ A + ∠ B = ∠ BCD ;
两边同时减去 ∠A 得:∠ B = ∠ BCD – ∠ A ;
又 ∠ BCD – ∠ A < ∠ BCD;
故:∠ BCD > ∠ B;
同理可证: ∠BCD > ∠ A;
猜想正确!
结论:三角形的外角大于与它不相邻任何一个内角.
三、合作探究
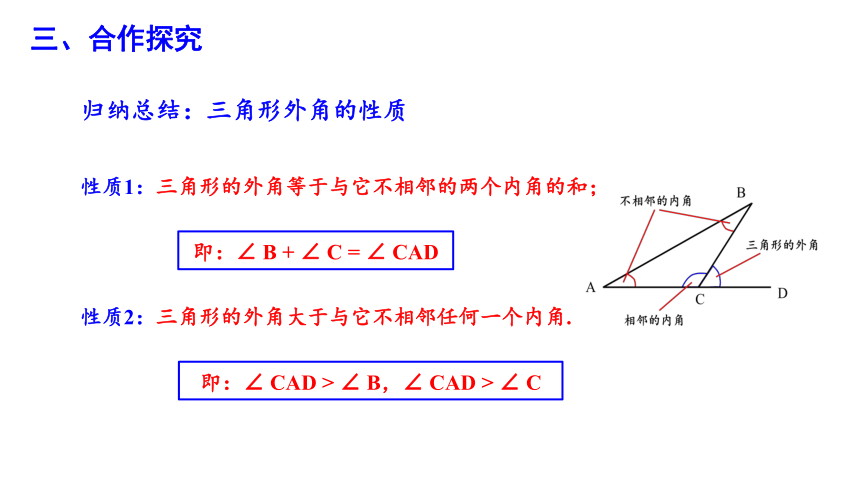
性质1:三角形的外角等于与它不相邻的两个内角的和;
性质2:三角形的外角大于与它不相邻任何一个内角.
即:∠ B + ∠ C = ∠ CAD
即:∠ CAD > ∠ B,∠ CAD > ∠ C
归纳总结:三角形外角的性质
三、合作探究
三、合作探究
练一练
1. 在△ABC中,∠B = ∠ACB = 70°且CD是∠ACB的角平分线,求∠1的度数.
分析:利用三角形的外角的性质 1 即可解答;
解:已知:∠ACB = 70°且CD是∠ACB的角平分线;
∴ ∠DCB = 35°;(角平分线定义)
∵ ∠1 是△ BCD的外角;
∴ ∠1 = ∠B +∠DCB = 105°(三角形的外角的性质).
A
B
C
D
1
2. 如图,已知在△ABC中, ∠A = 40°,∠1 = ∠2 且 PB、PC是角平分线,求:∠ACD的度数?
分析:利用三角形角平分线及外角的性质即可解答;
解:已知:PB、PC是角平分线,且∠ 1=∠2;
∴ ∠ ABC = 2 ∠ 1;∠ ACB = 2 ∠2 ;(角平分线的性质)
∴ ∠ ABC = ∠ ACB (等量代换)
∵ ∠A = 40°; ∴ ∠ ABC = ∠ ACB = 70°;(三角形内角和定理)
∴ ∠ ACD = ∠A+ ∠ ABC = 110°(三角形外角的性质)
A
B
C
P
D
1
2
三、合作探究
三、合作探究
3. 如图,用“ > ”连接 ∠1、∠2、∠3、∠4 为 .
【提示】根据三角形外角的性质 2 解答即可;
∠3 > ∠1 > ∠2 > ∠4
探究二:三角形的外角和
问题提出:前面我们已经知道了三角形的内角和为180°,那么三角形的外角和为多少?
问题探究:在 △ABC 中,有 个外角;
6
不是
规定:每个内角只取一个与其相邻的外角相加,它们的和即是外角和;
如:△ABC 的外角和为:∠1 + ∠3 + ∠5 或 ∠2 + ∠4 + ∠6 .
三、合作探究
1
2
3
4
5
6
B
C
A
思考:三角形的外角和是6个外角相加的和吗?
问题解决:三角形的外角和为 ∠1 + ∠3 + ∠5;
由图可知:∠1 + ∠BAC = 180°;
∠3 + ∠ABC = 180°;
∠5 + ∠BCA = 180°;
则:∠1 + ∠BAC + ∠3 + ∠ABC + ∠5 + ∠BCA = 3×180°;
又:∠BAC + ∠ABC + ∠BCA = 180°;
故:∠1 + ∠3 + ∠5 = 360°;
三、合作探究
1
3
5
B
C
A
结论:三角形的外角和为360°.
易错点:三角形的外角和是分别取
与内角相邻的一个外角相加的和.
三、合作探究
练一练
分析: ∵∠1、∠2、∠3 分别是△ABN、△CDP、△EFM的外角;
∴ ∠1 = ∠A + ∠B,∠2 = ∠C + ∠D,∠3 = ∠E + ∠F;
∴ ∠ A +∠ B +∠ C +∠ D +∠ E +∠ F = ∠ 1 + ∠ 2 + ∠ 3 ;
又 ∠ 1 + ∠ 2 + ∠ 3 是 △PMN 的外角和;
∴ ∠ A +∠ B +∠ C +∠ D +∠ E +∠ F = ∠ 1 + ∠ 2 + ∠ 3 = 360°
4. 如图,试求出 ∠A + ∠B + ∠C + ∠D + ∠E + ∠F = ________.
360°
1. 判断下列说法的对错.
(1)三角形的外角和是指三角形的所有外角的和; ( )
(2)三角形的外角和等于它的内角和的2倍; ( )
(3)三角形的一个外角等于两个内角的和; ( )
(4)三角形的一个外角等于与它不相邻的两个内角的和; ( )
(5)三角形的一个外角大于任何一个内角; ( )
(6)三角形的一个内角小于任何一个与它不相邻的外角. ( )
×
√
×
×
√
√
四、当堂检测
2. 如图,AB//CD,∠A = 37°,∠C = 63°,那么 ∠F 等于( )
A. 26° B. 63° C. 37° D. 60°
F
A
B
E
C
D
A
四、当堂检测
3. 如图,D是△ABC的BC边上一点,∠B =∠BAD,∠ADC=80°,∠BAC=70°,求:(1)∠B 的度数; (2)∠C的度数.
解:
(1)∵ ∠ADC是△ABD的外角;
∴ ∠ADC = ∠B+∠BAD = 80°.
又∵ ∠B = ∠BAD,
∴ ∠ = 80°×0.5 = 40°.
A
B
C
D
(2)在△ABC中,∠ B + ∠ BAC + ∠ C = 180°,
∠C = 180°- 40°- 70°= 70°.
四、当堂检测
A
B
C
D
E
解:∵ ∠1是△FBE的外角;
∴ ∠1 = ∠B+ ∠E,
∴ 同理∠2 = ∠A+∠D.
∵ 在△CFG中,∠C+∠1+∠2=180°,
∴ ∠A +∠B + ∠C +∠D + ∠E = 180°.
4. 如图,求∠ A + ∠ B + ∠ C + ∠ D + ∠ E 的度数.
2
1
F
G
四、当堂检测
五、课堂总结
三角形的外角
性质 1:
三角形的一个外角等于与它不相邻的两个内角的和;
外角和:三角形的外角和为 360°;
性质 2:
三角形的一个外角大于任何一个与它不相邻的内角;
第九章 多边形
9.1 三角形
9.1.2 三角形的内角和与外角和 第2课时
学习导航
学习目标
合作探究
当堂检测
课堂总结
新课导入
一、学习目标
1. 知道三角形的外角和等于 360°;
2. 掌握三角形外角的两条性质,能利用三角形的外角性质解决简单问题.(重点)
二、新课导入
思考:上节课同学们学习了三角形的内角和为180°,那么请同学们想一想,三角形的外角和该是多少度呢?
1
2
3
4
5
6
B
C
A
问题 1:观察图形:三角形的外角和它相邻的内角有什么关系呢
外角
相邻内角
三角形的外角和它相邻的内角组成一个平角!
三、合作探究
探究一:三角形外角的性质
即:三角形的外角和它相邻的内角互补!
思考:三角形的外角和它不相邻的内角又有着什么关系呢?
问题2:如图,△ABC的外角∠BCD与∠ A + ∠ B有什么关系?
提出猜想:① ∠ BCD > ∠ A + ∠ B;
② ∠ BCD < ∠ A + ∠ B;
③ ∠ BCD = ∠ A + ∠ B;
某小组提出了如下猜想,请你判断是否正确,并说明理由;
分析:利用三角形内角和定理及平角的性质证明即可;
三、合作探究
证明:猜想 ③ 正确;
在△ ABC 中:∠ A + ∠ B + ∠ ACB = 180°
(三角形内角和定理);
又∠ ACD 是一个平角:即∠ ACB + ∠ DCB = 180°;
故: ∠ A + ∠ B = ∠ DCB (等量代换);
由上可知:猜想 ③ 正确;
结论:三角形的任一外角等于其不相邻的两内角之和.
三、合作探究
问题3:如图,△ABC的外角∠BCD与∠ A、∠ B 分别有什么关系?
提出猜想: ∠BCD > ∠ A;∠BCD > ∠ B;
分析:利用问题2的结论即可证明;
证明:已知:∠ A + ∠ B = ∠ BCD ;
两边同时减去 ∠A 得:∠ B = ∠ BCD – ∠ A ;
又 ∠ BCD – ∠ A < ∠ BCD;
故:∠ BCD > ∠ B;
同理可证: ∠BCD > ∠ A;
猜想正确!
结论:三角形的外角大于与它不相邻任何一个内角.
三、合作探究
性质1:三角形的外角等于与它不相邻的两个内角的和;
性质2:三角形的外角大于与它不相邻任何一个内角.
即:∠ B + ∠ C = ∠ CAD
即:∠ CAD > ∠ B,∠ CAD > ∠ C
归纳总结:三角形外角的性质
三、合作探究
三、合作探究
练一练
1. 在△ABC中,∠B = ∠ACB = 70°且CD是∠ACB的角平分线,求∠1的度数.
分析:利用三角形的外角的性质 1 即可解答;
解:已知:∠ACB = 70°且CD是∠ACB的角平分线;
∴ ∠DCB = 35°;(角平分线定义)
∵ ∠1 是△ BCD的外角;
∴ ∠1 = ∠B +∠DCB = 105°(三角形的外角的性质).
A
B
C
D
1
2. 如图,已知在△ABC中, ∠A = 40°,∠1 = ∠2 且 PB、PC是角平分线,求:∠ACD的度数?
分析:利用三角形角平分线及外角的性质即可解答;
解:已知:PB、PC是角平分线,且∠ 1=∠2;
∴ ∠ ABC = 2 ∠ 1;∠ ACB = 2 ∠2 ;(角平分线的性质)
∴ ∠ ABC = ∠ ACB (等量代换)
∵ ∠A = 40°; ∴ ∠ ABC = ∠ ACB = 70°;(三角形内角和定理)
∴ ∠ ACD = ∠A+ ∠ ABC = 110°(三角形外角的性质)
A
B
C
P
D
1
2
三、合作探究
三、合作探究
3. 如图,用“ > ”连接 ∠1、∠2、∠3、∠4 为 .
【提示】根据三角形外角的性质 2 解答即可;
∠3 > ∠1 > ∠2 > ∠4
探究二:三角形的外角和
问题提出:前面我们已经知道了三角形的内角和为180°,那么三角形的外角和为多少?
问题探究:在 △ABC 中,有 个外角;
6
不是
规定:每个内角只取一个与其相邻的外角相加,它们的和即是外角和;
如:△ABC 的外角和为:∠1 + ∠3 + ∠5 或 ∠2 + ∠4 + ∠6 .
三、合作探究
1
2
3
4
5
6
B
C
A
思考:三角形的外角和是6个外角相加的和吗?
问题解决:三角形的外角和为 ∠1 + ∠3 + ∠5;
由图可知:∠1 + ∠BAC = 180°;
∠3 + ∠ABC = 180°;
∠5 + ∠BCA = 180°;
则:∠1 + ∠BAC + ∠3 + ∠ABC + ∠5 + ∠BCA = 3×180°;
又:∠BAC + ∠ABC + ∠BCA = 180°;
故:∠1 + ∠3 + ∠5 = 360°;
三、合作探究
1
3
5
B
C
A
结论:三角形的外角和为360°.
易错点:三角形的外角和是分别取
与内角相邻的一个外角相加的和.
三、合作探究
练一练
分析: ∵∠1、∠2、∠3 分别是△ABN、△CDP、△EFM的外角;
∴ ∠1 = ∠A + ∠B,∠2 = ∠C + ∠D,∠3 = ∠E + ∠F;
∴ ∠ A +∠ B +∠ C +∠ D +∠ E +∠ F = ∠ 1 + ∠ 2 + ∠ 3 ;
又 ∠ 1 + ∠ 2 + ∠ 3 是 △PMN 的外角和;
∴ ∠ A +∠ B +∠ C +∠ D +∠ E +∠ F = ∠ 1 + ∠ 2 + ∠ 3 = 360°
4. 如图,试求出 ∠A + ∠B + ∠C + ∠D + ∠E + ∠F = ________.
360°
1. 判断下列说法的对错.
(1)三角形的外角和是指三角形的所有外角的和; ( )
(2)三角形的外角和等于它的内角和的2倍; ( )
(3)三角形的一个外角等于两个内角的和; ( )
(4)三角形的一个外角等于与它不相邻的两个内角的和; ( )
(5)三角形的一个外角大于任何一个内角; ( )
(6)三角形的一个内角小于任何一个与它不相邻的外角. ( )
×
√
×
×
√
√
四、当堂检测
2. 如图,AB//CD,∠A = 37°,∠C = 63°,那么 ∠F 等于( )
A. 26° B. 63° C. 37° D. 60°
F
A
B
E
C
D
A
四、当堂检测
3. 如图,D是△ABC的BC边上一点,∠B =∠BAD,∠ADC=80°,∠BAC=70°,求:(1)∠B 的度数; (2)∠C的度数.
解:
(1)∵ ∠ADC是△ABD的外角;
∴ ∠ADC = ∠B+∠BAD = 80°.
又∵ ∠B = ∠BAD,
∴ ∠ = 80°×0.5 = 40°.
A
B
C
D
(2)在△ABC中,∠ B + ∠ BAC + ∠ C = 180°,
∠C = 180°- 40°- 70°= 70°.
四、当堂检测
A
B
C
D
E
解:∵ ∠1是△FBE的外角;
∴ ∠1 = ∠B+ ∠E,
∴ 同理∠2 = ∠A+∠D.
∵ 在△CFG中,∠C+∠1+∠2=180°,
∴ ∠A +∠B + ∠C +∠D + ∠E = 180°.
4. 如图,求∠ A + ∠ B + ∠ C + ∠ D + ∠ E 的度数.
2
1
F
G
四、当堂检测
五、课堂总结
三角形的外角
性质 1:
三角形的一个外角等于与它不相邻的两个内角的和;
外角和:三角形的外角和为 360°;
性质 2:
三角形的一个外角大于任何一个与它不相邻的内角;
