8.3 一元一次不等式组 课件(共18张PPT) 华东师大版七年级数学下册
文档属性
| 名称 | 8.3 一元一次不等式组 课件(共18张PPT) 华东师大版七年级数学下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 264.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-19 00:00:00 | ||
图片预览





文档简介
(共18张PPT)
第八章 一元一次不等式
8.3 一元一次不等式组
学习导航
学习目标
合作探究
课堂总结
自主学习
新课导入
一、学习目标
1. 掌握一元一次不等式组、一元一次不等式组的解集的概念;
2. 会用数轴确定由两个一元一次不等式组成的不等式组的解集.
(重点)
二、新课导入
同学们的零花钱平时都花在哪?
零花钱正确使用姿势
练习题
书籍
零食饮料?
衣服饰品?
娱乐消费?
体育用品
献爱心
三、自主学习
情境1:小美带着自己的 5 元零花钱去超市买作业本,她拿了 5 本,结果在付款时钱不够,于是小美退掉一本,收银员找给她一些零钱 .
问题1:依据题意,你能得出几个不等关系?
作业本单价 × 5 > 5元;
作业本单价 × 4 < 5元 .
问题2:根据不等关系,我们应该怎样设未知数?
设作业本的单价为 x 元,可得:
5x > 5;
4x < 5.
知识点1:一元一次不等式组的概念及解法
三、自主学习
思考 1:类比方程组的概念,说出什么是一元一次不等式组?怎样表示?
由几个含有同一个未知数的一元一次不等式组成的不等式组叫做:一元一次不等式组
例:
5x > 5
4x < 5
易错误区:一元一次不等式组不一定是两个不等式组成,可以是多个一元一次不等式合在一起.
– 2
– 1
0
1
2
3
– 3
三、自主学习
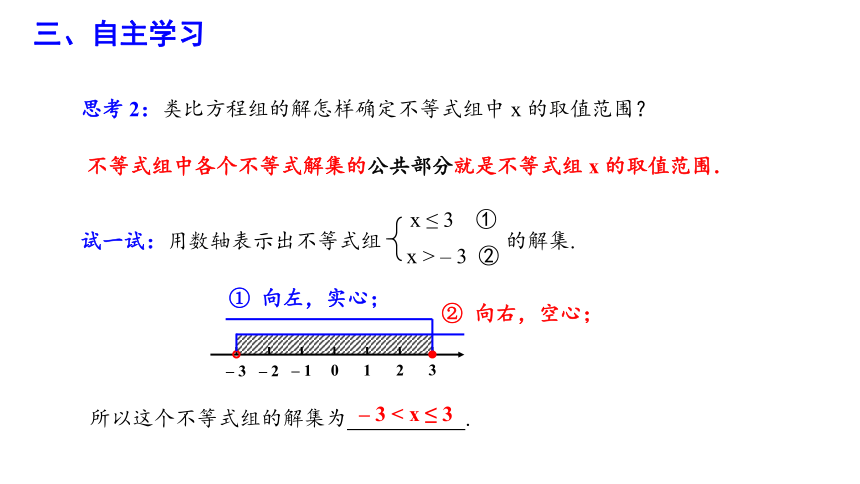
思考 2:类比方程组的解怎样确定不等式组中 x 的取值范围?
不等式组中各个不等式解集的公共部分就是不等式组 x 的取值范围.
试一试:用数轴表示出不等式组 的解集.
x ≤ 3 ①
x > – 3 ②
所以这个不等式组的解集为 .
– 3 < x ≤ 3
① 向左,实心;
② 向右,空心;
三、自主学习
(1)由几个含有同一个未知数的一元一次不等式组成的不等式组,叫做一元一次不等式组;
(2)几个一元一次不等式解集的公共部分,叫做这个一元一次不等式组的解集;
(3)求一元一次不等式解集的过程叫做解不等式组.
要点归纳:
探究一:一元一次不等式组的解法
四、合作探究
活动1:解下列不等式组,并把不等式组的解集在数轴上表示出来.
分析: 根据解不等式组的步骤,先分别求解,再在数轴上表示即可.
解:(1)
x – 1 > 0
x + 1 > 3
(1) ;(2) ;(3) ;(4) .
x – 1 < 0
x + 1 < 3
x – 1 > 0
x + 1 < 3
x – 1 < 0
x + 1 > 3
x – 1 > 0 ①
x + 1 > 3 ②
由 ① 得:x > 1;
由 ② 得:x > 2;
– 1
0
1
2
3
4
数轴表示:
不等式组的解集是 x > 2
注:“大大取大”.
(2)
x – 1 < 0 ①
x + 1 < 3 ②
由 ① 得:x < 1;
由 ② 得:x < 2;
– 1
0
1
2
3
4
数轴表示:
不等式组的解集是 x < 1
注:“小小取小”.
四、合作探究
x – 1 > 0
x + 1 > 3
(1) ;(2) ;(3) ;(4) .
x – 1 < 0
x + 1 < 3
x – 1 > 0
x + 1 < 3
x – 1 < 0
x + 1 > 3
(3)
x – 1 > 0 ①
x + 1 < 3 ②
由 ① 得:x > 1;
由 ② 得:x < 2;
– 1
0
1
2
3
4
数轴表示:
不等式组的解集是 1 < x < 2
注:“大小小大中间找”.
四、合作探究
x – 1 > 0
x + 1 > 3
(1) ;(2) ;(3) ;(4) .
x – 1 < 0
x + 1 < 3
x – 1 > 0
x + 1 < 3
x – 1 < 0
x + 1 > 3
(4)
x – 1 < 0 ①
x + 1 > 3 ②
由 ① 得:x < 1;
由 ② 得:x > 2;
– 1
0
1
2
3
4
数轴表示:
该不等式组无解
注:“大大小小解不了”.
四、合作探究
x – 1 > 0
x + 1 > 3
(1) ;(2) ;(3) ;(4) .
x – 1 < 0
x + 1 < 3
x – 1 > 0
x + 1 < 3
x – 1 < 0
x + 1 > 3
归纳总结 1
不等式组 数轴表示 解集 规律
x > 1
x > 2
x < 1
x < 2
x > 1
x < 2
x < 1
x > 2
x > 2
x < 1
1 < x < 2
无解
大大取大
(两个大于取更大的那个)
小小取小
(两个小于取更小的那个)
大小小大中间找
(大于小的数,小于大的数)
大大小小解不了
(大于大的数,小于小的数)
四、合作探究
(1)解不等式组的一般步骤:
① 分别解每一个不等式;
② 在同一数轴上表示每个不等式的解集;
③ 找出各不等式解集的公共部分.
四、合作探究
归纳总结 2
① 大于向右画,小于向左画;
② 有等号的画实心圆点,无等号的画空心圆圈.
(2)在数轴上表示不等式的解集时应注意:
四、合作探究
练一练
1.解下列不等式组 ,并在数轴上表示出来.
①
②
分析:分别解每一个不等式,再在数轴上标出即可求解;
由不等式 ② 得:4 > x ,即 x < 4;
在数轴表示:
解:由不等式 ① 得:2x > 2,即 x > 1;
0
1
2
3
4
5
不等式组的解集是 1 < x < 4
注:“大小小大中间找”
探究二:一元一次不等式组的应用
四、合作探究
活动2:幼儿园老师给30个小朋友发糖果,每人发5个,结果小明哭了;其他人都有5个,只有他虽然有但不够5个,请问老师拿来多少糖果?
问题探究:已知:糖果总数量 = 5个×29人 + 小明的糖果数;
其中小明最少可以分到: 个;
最多可以分到: 个;
30
29
1
4
问题解决:设共有 x 个糖果;
找出不等关系:① 糖果总数量 < ×5;② 糖果总数量 > ×5.
x > 29×5 ①
x < 30×5 ②
可列出下列不等式组:
解得:
145 < x < 150;
故 x 可取 146、147、148、149.
因为 x 只能取整数;
答:老师可能拿了 146、147、148 或 149 个糖果.
四、合作探究
练一练
2. 有若干学生参加夏令营活动,晚上在一宾馆住宿时,如果每间住4个,那么还有20人住不下,相同的房间,如果每间住8人,那么还有一间住不满也不空,请问:这群学生有多少人?有多少房间供他们住?
解:设有 x 间房供他们住,则学生有 ( 4x + 20 ) 人;
解得:5 < x < 7;
(4x + 20) – 8 (x – 1) > 0
(4x + 20) – 8 (x – 1) < 8
答:有学生 44 人,有 6 间房供他们住.
根据题意,x 的值应是整数,所以 x = 6;4x + 20 = 44人.
由题意得:
五、课堂总结
第八章 一元一次不等式
8.3 一元一次不等式组
学习导航
学习目标
合作探究
课堂总结
自主学习
新课导入
一、学习目标
1. 掌握一元一次不等式组、一元一次不等式组的解集的概念;
2. 会用数轴确定由两个一元一次不等式组成的不等式组的解集.
(重点)
二、新课导入
同学们的零花钱平时都花在哪?
零花钱正确使用姿势
练习题
书籍
零食饮料?
衣服饰品?
娱乐消费?
体育用品
献爱心
三、自主学习
情境1:小美带着自己的 5 元零花钱去超市买作业本,她拿了 5 本,结果在付款时钱不够,于是小美退掉一本,收银员找给她一些零钱 .
问题1:依据题意,你能得出几个不等关系?
作业本单价 × 5 > 5元;
作业本单价 × 4 < 5元 .
问题2:根据不等关系,我们应该怎样设未知数?
设作业本的单价为 x 元,可得:
5x > 5;
4x < 5.
知识点1:一元一次不等式组的概念及解法
三、自主学习
思考 1:类比方程组的概念,说出什么是一元一次不等式组?怎样表示?
由几个含有同一个未知数的一元一次不等式组成的不等式组叫做:一元一次不等式组
例:
5x > 5
4x < 5
易错误区:一元一次不等式组不一定是两个不等式组成,可以是多个一元一次不等式合在一起.
– 2
– 1
0
1
2
3
– 3
三、自主学习
思考 2:类比方程组的解怎样确定不等式组中 x 的取值范围?
不等式组中各个不等式解集的公共部分就是不等式组 x 的取值范围.
试一试:用数轴表示出不等式组 的解集.
x ≤ 3 ①
x > – 3 ②
所以这个不等式组的解集为 .
– 3 < x ≤ 3
① 向左,实心;
② 向右,空心;
三、自主学习
(1)由几个含有同一个未知数的一元一次不等式组成的不等式组,叫做一元一次不等式组;
(2)几个一元一次不等式解集的公共部分,叫做这个一元一次不等式组的解集;
(3)求一元一次不等式解集的过程叫做解不等式组.
要点归纳:
探究一:一元一次不等式组的解法
四、合作探究
活动1:解下列不等式组,并把不等式组的解集在数轴上表示出来.
分析: 根据解不等式组的步骤,先分别求解,再在数轴上表示即可.
解:(1)
x – 1 > 0
x + 1 > 3
(1) ;(2) ;(3) ;(4) .
x – 1 < 0
x + 1 < 3
x – 1 > 0
x + 1 < 3
x – 1 < 0
x + 1 > 3
x – 1 > 0 ①
x + 1 > 3 ②
由 ① 得:x > 1;
由 ② 得:x > 2;
– 1
0
1
2
3
4
数轴表示:
不等式组的解集是 x > 2
注:“大大取大”.
(2)
x – 1 < 0 ①
x + 1 < 3 ②
由 ① 得:x < 1;
由 ② 得:x < 2;
– 1
0
1
2
3
4
数轴表示:
不等式组的解集是 x < 1
注:“小小取小”.
四、合作探究
x – 1 > 0
x + 1 > 3
(1) ;(2) ;(3) ;(4) .
x – 1 < 0
x + 1 < 3
x – 1 > 0
x + 1 < 3
x – 1 < 0
x + 1 > 3
(3)
x – 1 > 0 ①
x + 1 < 3 ②
由 ① 得:x > 1;
由 ② 得:x < 2;
– 1
0
1
2
3
4
数轴表示:
不等式组的解集是 1 < x < 2
注:“大小小大中间找”.
四、合作探究
x – 1 > 0
x + 1 > 3
(1) ;(2) ;(3) ;(4) .
x – 1 < 0
x + 1 < 3
x – 1 > 0
x + 1 < 3
x – 1 < 0
x + 1 > 3
(4)
x – 1 < 0 ①
x + 1 > 3 ②
由 ① 得:x < 1;
由 ② 得:x > 2;
– 1
0
1
2
3
4
数轴表示:
该不等式组无解
注:“大大小小解不了”.
四、合作探究
x – 1 > 0
x + 1 > 3
(1) ;(2) ;(3) ;(4) .
x – 1 < 0
x + 1 < 3
x – 1 > 0
x + 1 < 3
x – 1 < 0
x + 1 > 3
归纳总结 1
不等式组 数轴表示 解集 规律
x > 1
x > 2
x < 1
x < 2
x > 1
x < 2
x < 1
x > 2
x > 2
x < 1
1 < x < 2
无解
大大取大
(两个大于取更大的那个)
小小取小
(两个小于取更小的那个)
大小小大中间找
(大于小的数,小于大的数)
大大小小解不了
(大于大的数,小于小的数)
四、合作探究
(1)解不等式组的一般步骤:
① 分别解每一个不等式;
② 在同一数轴上表示每个不等式的解集;
③ 找出各不等式解集的公共部分.
四、合作探究
归纳总结 2
① 大于向右画,小于向左画;
② 有等号的画实心圆点,无等号的画空心圆圈.
(2)在数轴上表示不等式的解集时应注意:
四、合作探究
练一练
1.解下列不等式组 ,并在数轴上表示出来.
①
②
分析:分别解每一个不等式,再在数轴上标出即可求解;
由不等式 ② 得:4 > x ,即 x < 4;
在数轴表示:
解:由不等式 ① 得:2x > 2,即 x > 1;
0
1
2
3
4
5
不等式组的解集是 1 < x < 4
注:“大小小大中间找”
探究二:一元一次不等式组的应用
四、合作探究
活动2:幼儿园老师给30个小朋友发糖果,每人发5个,结果小明哭了;其他人都有5个,只有他虽然有但不够5个,请问老师拿来多少糖果?
问题探究:已知:糖果总数量 = 5个×29人 + 小明的糖果数;
其中小明最少可以分到: 个;
最多可以分到: 个;
30
29
1
4
问题解决:设共有 x 个糖果;
找出不等关系:① 糖果总数量 < ×5;② 糖果总数量 > ×5.
x > 29×5 ①
x < 30×5 ②
可列出下列不等式组:
解得:
145 < x < 150;
故 x 可取 146、147、148、149.
因为 x 只能取整数;
答:老师可能拿了 146、147、148 或 149 个糖果.
四、合作探究
练一练
2. 有若干学生参加夏令营活动,晚上在一宾馆住宿时,如果每间住4个,那么还有20人住不下,相同的房间,如果每间住8人,那么还有一间住不满也不空,请问:这群学生有多少人?有多少房间供他们住?
解:设有 x 间房供他们住,则学生有 ( 4x + 20 ) 人;
解得:5 < x < 7;
(4x + 20) – 8 (x – 1) > 0
(4x + 20) – 8 (x – 1) < 8
答:有学生 44 人,有 6 间房供他们住.
根据题意,x 的值应是整数,所以 x = 6;4x + 20 = 44人.
由题意得:
五、课堂总结
