9.1.2 三角形的内角和与外角和 第1课时 课件 (共18张PPT)华东师大版七年级数学下册
文档属性
| 名称 | 9.1.2 三角形的内角和与外角和 第1课时 课件 (共18张PPT)华东师大版七年级数学下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 255.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-19 18:07:08 | ||
图片预览




文档简介
(共18张PPT)
第九章 多边形
9.1 三角形
9.1.2 三角形的内角和与外角和 第1课时
学习导航
学习目标
合作探究
当堂检测
课堂总结
新课导入
一、学习目标
1.能利用平行线的性质证明三角形内角和定理,并能推出直角三角形的两锐角互余;(重点)
3.能利用三角形的内角和定理解决一些简单问题;
二、新课导入
辨一辨:
一天,三类三角形通过对自身的特点,讲出了自己对三角形内角和的理解,请同学们帮它们分辨一下吧.
不对,我有一个钝角,所以我的内角和才是最大的
我的形状最大,那我的内角和最大.
我的形状最小,我的内角和也最小
三、合作探究
探究一:三角形的内角和
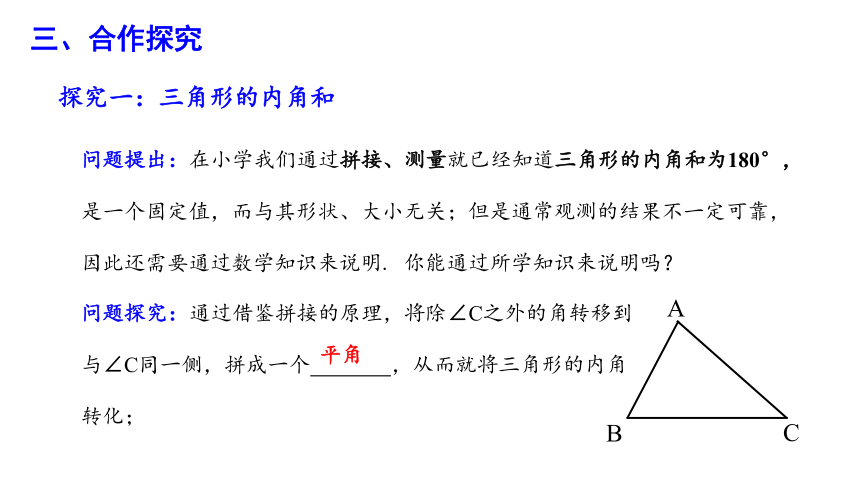
问题提出:在小学我们通过拼接、测量就已经知道三角形的内角和为180°,是一个固定值,而与其形状、大小无关;但是通常观测的结果不一定可靠,因此还需要通过数学知识来说明. 你能通过所学知识来说明吗?
问题探究:通过借鉴拼接的原理,将除∠C之外的角转移到
与∠C同一侧,拼成一个 ,从而就将三角形的内角转化;
平角
C
B
A
三、合作探究
则有:∠A = ∠1;(两直线平行,内错角相等)
∠B = ∠2;(两直线平行,同位角相等)
又因为 ∠1 + ∠2 + ∠ACB = 180°,
所以 ∠A + ∠B + ∠ACB = 180°.
C
B
A
E
D
1
2
问题解决:延长BC到D,过点C作CE∥BA;
注意:关键思想是转化思想!
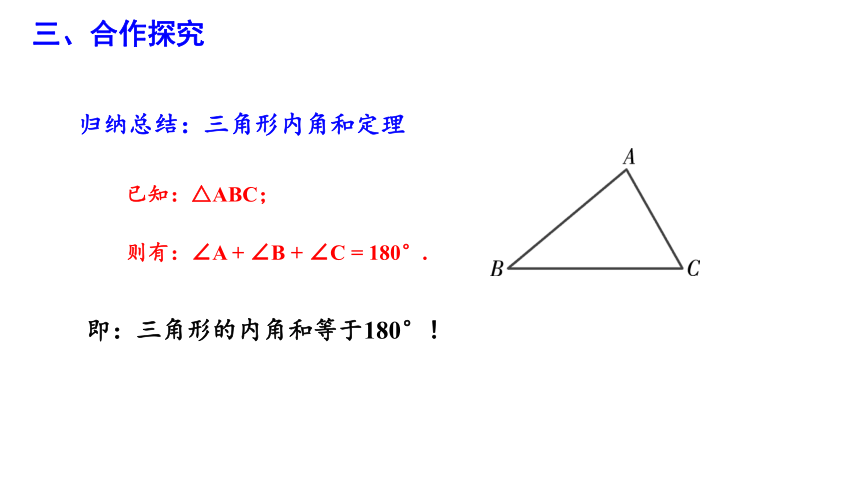
即:三角形的内角和等于180°!
则有:∠A + ∠B + ∠C = 180°.
已知:△ABC;
归纳总结:三角形内角和定理
三、合作探究
三、合作探究
1. 如图,在△ABC中, ∠BAC=40 °, ∠B=80 °,AD是△ABC的角平分线,求∠ADB的度数.
解:由∠BAC = 40 °, AD是△ABC的角平分线;
A
B
C
D
练一练
得:∠BAD = ∠BAC = 20 °;
在 △ABD中:∠ADB = 180°– ∠B – ∠BAD
= 180°– 80°– 20°
= 80°.
2. 如图, ∠C = ∠D = 90 °,AD、BC 相交于点E. ∠CAE 与 ∠DBE 有什么关系?为什么?
解:相等关系;
因为:在Rt△ACE中,∠CAE = 90°– ∠AEC;
在Rt△BDE中,∠DBE = 90°– ∠BED;
又因为:∠AEC = ∠BED;
所以:∠CAE = ∠DBE .
A
B
C
D
E
三、合作探究
探究二:直角三角形的性质
问题提出:我们可以按三角形内角的大小把三角形分为:锐角三角形、直角三角形、钝角三角形. 通常用符号“Rt△ ABC”表示“直角三角形ABC”,那么如图,在Rt△ABC中, ∠C = 90°,两个锐角之间有什么关系呢?
问题探究:在 Rt△ABC 中,因为 ∠C = 90°;
由 可知:∠A + ∠B + ∠C = 180°;
即 ∠A + ∠B = .
三角形内角和定理
90°
问题解决:两个锐角之和为90°;
总结:直角三角形的两个锐角互余.
三、合作探究
三、合作探究
练一练
3. 如图,在Rt△ABC中,若∠A = 50°,则∠ B = ( )
A.40° B.50° C.40°或50° D.40°或90°
D
分析:根据直角三角形两个锐角之和为90°,并 ∠A = 50°可得:
有一锐角必为40°;
又不知 ∠ B 是直角还是锐角,所以 ∠ B 为40°或90°,故选D.
探究三:三角形内角和定理的简单应用
问题 1:如图,C 岛在 A 岛的北偏东50°方向,B 岛在 A 岛的北偏东 80 °方向,C 岛在 B 岛的北偏西 40 °方向;从 B 岛看 A,C 两岛的视角 ∠ABC
是多少度?从 C 岛看 A、B 两岛的视角 ∠ACB 是多少度?
分析:运用平行线的性质和三角形内角和定理解答即可;
三、合作探究
已知:C 岛在 A 岛的北偏东50°;B 岛在 A 岛的北偏东 80 °方向,C 岛在 B 岛的北偏西 40 °方向;求 ∠ABC 、∠ACB 是多少度?
解:如图,因为 ∠DAC = 50°、∠DAB = 80°;
所以 ∠CAB = 30°;
由 AD // BE,得 ∠DAB + ∠EBA = 180 °;
所以 ∠EBA = 180 °– 80°= 100°;
因为 ∠EBC = 40°;
所以 ∠ABC = 100 °– 40°= 60°;
所以 ∠ACB = 180 °– 30°– 60°= 90°.
三、合作探究
练一练:
4.如图:点 A 位于点 O 的 方向;
点 B 位于点 O 的 方向;
点 C 位于点 O 的 方向.
北偏东15°
南偏东30°
西偏南45°
三、合作探究
四、当堂检测
1.如图,在△ABC中,BE、CD分别平分∠ABC和∠ACB,若∠1=50°,则∠A等于( )
A.60° B.70° C.80° D.140°
C
2.直角三角形的一个锐角∠A是另一个锐角∠B的3倍,那么∠B的度数是
( )
A.22.5° B.45° C.67.5° D.135°
A
四、当堂检测
3. 如图,四边形 ABCD 中,点 E 在 BC 上,∠A + ∠ADE = 180°,∠B=78°,∠C = 60°,求 ∠EDC 的度数.
解:∵ ∠ A + ∠ ADE = 180°;
∴ AB∥DE;
∴ ∠ CED = ∠ B = 78°;
又∵ ∠ C = 60°;
∴ ∠ EDC = 180°– ( ∠ CED + ∠ C )
= 180°– ( 78°+ 60°)
= 42°.
A
D
C
B
E
4. 如图,△ABC中 BD⊥AC,垂足为D,∠ABD=54°,∠DBC=18°,求∠A和∠C的度数.
四、当堂检测
解:∵ BD ⊥ AC,∴ ∠ADB = ∠CDB = 90°
在△ABD中 ∠A 与 ∠ABD 互余,又∠ABD = 54°;
∴ ∠A = 90°– 54°= 36°;
在△CBD中 ∠C 与 ∠CBD 互余,又∠DBC = 18°;
∴ ∠C = 90°– 18°= 72°.
五、课堂总结
三角形的内角和定理
定理:三角形的内角和为 180°;
推论:直角三角形的两锐角之和为 90°.
第九章 多边形
9.1 三角形
9.1.2 三角形的内角和与外角和 第1课时
学习导航
学习目标
合作探究
当堂检测
课堂总结
新课导入
一、学习目标
1.能利用平行线的性质证明三角形内角和定理,并能推出直角三角形的两锐角互余;(重点)
3.能利用三角形的内角和定理解决一些简单问题;
二、新课导入
辨一辨:
一天,三类三角形通过对自身的特点,讲出了自己对三角形内角和的理解,请同学们帮它们分辨一下吧.
不对,我有一个钝角,所以我的内角和才是最大的
我的形状最大,那我的内角和最大.
我的形状最小,我的内角和也最小
三、合作探究
探究一:三角形的内角和
问题提出:在小学我们通过拼接、测量就已经知道三角形的内角和为180°,是一个固定值,而与其形状、大小无关;但是通常观测的结果不一定可靠,因此还需要通过数学知识来说明. 你能通过所学知识来说明吗?
问题探究:通过借鉴拼接的原理,将除∠C之外的角转移到
与∠C同一侧,拼成一个 ,从而就将三角形的内角转化;
平角
C
B
A
三、合作探究
则有:∠A = ∠1;(两直线平行,内错角相等)
∠B = ∠2;(两直线平行,同位角相等)
又因为 ∠1 + ∠2 + ∠ACB = 180°,
所以 ∠A + ∠B + ∠ACB = 180°.
C
B
A
E
D
1
2
问题解决:延长BC到D,过点C作CE∥BA;
注意:关键思想是转化思想!
即:三角形的内角和等于180°!
则有:∠A + ∠B + ∠C = 180°.
已知:△ABC;
归纳总结:三角形内角和定理
三、合作探究
三、合作探究
1. 如图,在△ABC中, ∠BAC=40 °, ∠B=80 °,AD是△ABC的角平分线,求∠ADB的度数.
解:由∠BAC = 40 °, AD是△ABC的角平分线;
A
B
C
D
练一练
得:∠BAD = ∠BAC = 20 °;
在 △ABD中:∠ADB = 180°– ∠B – ∠BAD
= 180°– 80°– 20°
= 80°.
2. 如图, ∠C = ∠D = 90 °,AD、BC 相交于点E. ∠CAE 与 ∠DBE 有什么关系?为什么?
解:相等关系;
因为:在Rt△ACE中,∠CAE = 90°– ∠AEC;
在Rt△BDE中,∠DBE = 90°– ∠BED;
又因为:∠AEC = ∠BED;
所以:∠CAE = ∠DBE .
A
B
C
D
E
三、合作探究
探究二:直角三角形的性质
问题提出:我们可以按三角形内角的大小把三角形分为:锐角三角形、直角三角形、钝角三角形. 通常用符号“Rt△ ABC”表示“直角三角形ABC”,那么如图,在Rt△ABC中, ∠C = 90°,两个锐角之间有什么关系呢?
问题探究:在 Rt△ABC 中,因为 ∠C = 90°;
由 可知:∠A + ∠B + ∠C = 180°;
即 ∠A + ∠B = .
三角形内角和定理
90°
问题解决:两个锐角之和为90°;
总结:直角三角形的两个锐角互余.
三、合作探究
三、合作探究
练一练
3. 如图,在Rt△ABC中,若∠A = 50°,则∠ B = ( )
A.40° B.50° C.40°或50° D.40°或90°
D
分析:根据直角三角形两个锐角之和为90°,并 ∠A = 50°可得:
有一锐角必为40°;
又不知 ∠ B 是直角还是锐角,所以 ∠ B 为40°或90°,故选D.
探究三:三角形内角和定理的简单应用
问题 1:如图,C 岛在 A 岛的北偏东50°方向,B 岛在 A 岛的北偏东 80 °方向,C 岛在 B 岛的北偏西 40 °方向;从 B 岛看 A,C 两岛的视角 ∠ABC
是多少度?从 C 岛看 A、B 两岛的视角 ∠ACB 是多少度?
分析:运用平行线的性质和三角形内角和定理解答即可;
三、合作探究
已知:C 岛在 A 岛的北偏东50°;B 岛在 A 岛的北偏东 80 °方向,C 岛在 B 岛的北偏西 40 °方向;求 ∠ABC 、∠ACB 是多少度?
解:如图,因为 ∠DAC = 50°、∠DAB = 80°;
所以 ∠CAB = 30°;
由 AD // BE,得 ∠DAB + ∠EBA = 180 °;
所以 ∠EBA = 180 °– 80°= 100°;
因为 ∠EBC = 40°;
所以 ∠ABC = 100 °– 40°= 60°;
所以 ∠ACB = 180 °– 30°– 60°= 90°.
三、合作探究
练一练:
4.如图:点 A 位于点 O 的 方向;
点 B 位于点 O 的 方向;
点 C 位于点 O 的 方向.
北偏东15°
南偏东30°
西偏南45°
三、合作探究
四、当堂检测
1.如图,在△ABC中,BE、CD分别平分∠ABC和∠ACB,若∠1=50°,则∠A等于( )
A.60° B.70° C.80° D.140°
C
2.直角三角形的一个锐角∠A是另一个锐角∠B的3倍,那么∠B的度数是
( )
A.22.5° B.45° C.67.5° D.135°
A
四、当堂检测
3. 如图,四边形 ABCD 中,点 E 在 BC 上,∠A + ∠ADE = 180°,∠B=78°,∠C = 60°,求 ∠EDC 的度数.
解:∵ ∠ A + ∠ ADE = 180°;
∴ AB∥DE;
∴ ∠ CED = ∠ B = 78°;
又∵ ∠ C = 60°;
∴ ∠ EDC = 180°– ( ∠ CED + ∠ C )
= 180°– ( 78°+ 60°)
= 42°.
A
D
C
B
E
4. 如图,△ABC中 BD⊥AC,垂足为D,∠ABD=54°,∠DBC=18°,求∠A和∠C的度数.
四、当堂检测
解:∵ BD ⊥ AC,∴ ∠ADB = ∠CDB = 90°
在△ABD中 ∠A 与 ∠ABD 互余,又∠ABD = 54°;
∴ ∠A = 90°– 54°= 36°;
在△CBD中 ∠C 与 ∠CBD 互余,又∠DBC = 18°;
∴ ∠C = 90°– 18°= 72°.
五、课堂总结
三角形的内角和定理
定理:三角形的内角和为 180°;
推论:直角三角形的两锐角之和为 90°.
